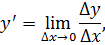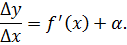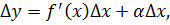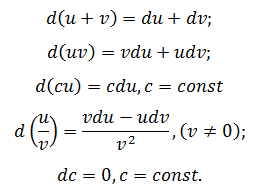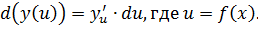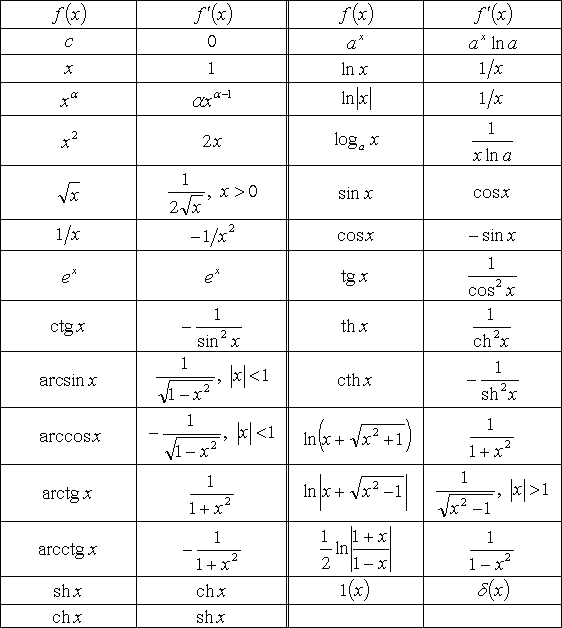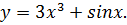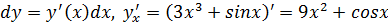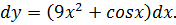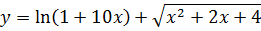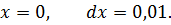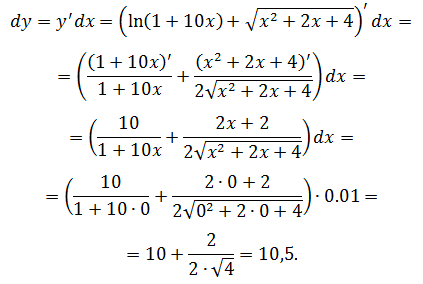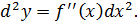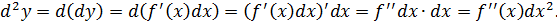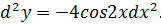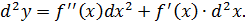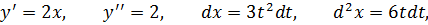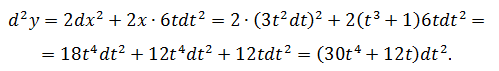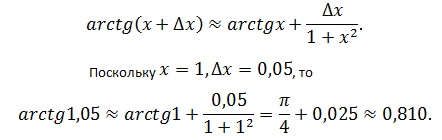что такое дифференцирование в математике
Правила дифференцирования: доказательство и примеры
Чтобы успешно решать задачи на дифференцирование, нужно уметь находить разные виды производных. Данная статья посвящена основным правилам дифференцирования, которые постоянно используются на практике. С помощью самого определения производной функции мы сформулируем доказательства всех этих правил и подробно рассмотрим несколько примеров, чтобы понять, как они применяются при решении задач.
Сформулируем основные проблемы дифференцирования:
Разберем все эти случаи по порядку.
Как вынести постоянный множитель за знак производной
Для начала нам нужно доказать следующую формулу:
Используя определение производной, запишем следующее:
Этим мы доказали первое правило дифференцирования. Разберем задачу на его применение.
Решение
Вынесем множитель за знак производной и получим:
Это самый простой пример. На практике чаще всего приходится предварительно преобразовывать дифференцируемую функцию, чтобы увидеть нужное значение в таблице производных и применить соответствующее правило.
Решение
Решение
Сначала нам нужно выполнить преобразование исходной функции.
Далее применяем изученное выше правило и берем из таблицы производных соответствующее значение:
Как вычислить производную суммы и производную разности
Так мы можем доказать равенство производной суммы или разности n-ного количества функций сумме или разности их производных:
Решение
Первым делом упрощаем данную функцию.
После этого применяем второе правило – производной суммы/разности:
Первое правило говорит нам о том, что можно вынести постоянный множитель за знак производной, значит:
Нам остается только заглянуть в таблицу производных и взять оттуда соответствующее значение:
Как вычислить производную произведения функций
Правило дифференцирования произведения двух функций выглядит следующим образом: f x · g ( x ) ‘ = f ‘ ( x ) · g ( x ) ‘ + f ( x ) · g ‘ ( x )
Попробуем доказать его.
Это и есть результат, который нам нужно было доказать.
Решение
y ‘ = ( t g x · a r c sin x ) ‘ = ( t g x ) ‘ · a r c sin x + t g x · ( a r c sin x ) ‘
Берем нужное значение из таблицы производных основных элементарных функций и записываем ответ:
Решение
Теперь разберем, что нужно делать в случае, когда производную нужно найти для произведения трех функций. По той же схеме решаются задачи с произведениями четырех, пяти и большего количества функций.
Решение
У нас получится следующее:
y ‘ = ( ( 1 + x ) · sin x · ln x ) ‘ = 1 + x · sin x ‘ · ln x + 1 + x · sin x · ln x ‘
1 + x · sin x ‘ = ( 1 + x ) ‘ · sin x + 1 + x · ( sin x ) ‘
С помощью этого правила и таблицы производных получим:
Теперь подставим в формулу то, что у нас получилось:
y ‘ = 1 + x · sin x · ln x ‘ = 1 + x · sin x ‘ · ln x + ( 1 + x ) · sin x · ( ln x ) ‘ = = sin x + cos x + x · cos x · ln x + ( 1 + x ) · sin x x
Ответ: y ‘ = sin x + cos x + x · cos x · ln x + ( 1 + x ) · sin x x
Из этого примера видно, что иногда приходится применять несколько правил дифференцирования подряд для вычисления нужного результата. Это не так сложно, как кажется, главное – соблюдать нужную последовательность действий.
Решение
Как вычислить производную частного двух функций (дробного выражения с функциями)
Сразу отметим, что g ( x ) не будет обращаться в 0 ни при каких значениях x из указанного промежутка. Согласно определению производной, получим:
Решение
После этого нам потребуется правило для суммы, а также правило вынесения постоянного множителя за знак производной:
Возьмем задачу на применение всех изученных правил.
Решение
Поясним, как это получилось.
Вычисляем третье слагаемое:
Теперь собираем все, что у нас получилось:
В задачах, которые мы разобрали в этой статье, использовались только основные элементарные функции, которые были связаны между собой знаками простых арифметических действий. Они нагляднее всего иллюстрируют правила дифференцирования. Однако возможно их применение и к более сложным функциям.
После того, как мы разберем, что такое производная сложной функции, мы сможете проводить дифференцирование выражений любой сложности.
Решение производной для чайников: определение, как найти, примеры решений
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Таблица производных функций
10 класс, 11 класс, ЕГЭ/ОГЭ
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
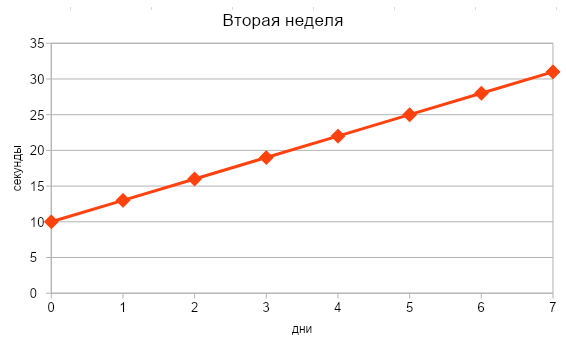
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:
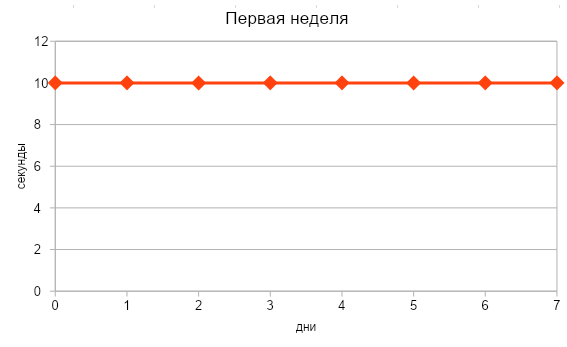
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Приведем несколько формул, которых достаточно для решения большинства задач.
Дифференцирование функции, нахождение производной
Если вам нужно решить задачу, в рамках которой требуется вычислить производную какой-либо функции с одной переменной, советуем внимательно прочесть эту статью. Здесь приводятся общие положения теории дифференцирования, имеющие отношение к вычислению производной. Для этого могут быть использованы разные способы, ведь исходная функция может быть задана явно или неявно, в параметрическом виде, быть элементарной, основной или сложной, значит, в каждой ситуации бывает нужен свой подход.
Таблица дифференцирования функции
Мы собрали всю информацию, которую нужно знать для правильного дифференцирования функции, и представили ее в табличном виде:
Степенная фунция y = x p
y = a x a x ‘ = a x · ln a
В частности, при a = e имеем
log a x ‘ = 1 x · ln a
В частности, при a = e имеем
y = ln x ln x ‘ = 1 x
Производная сложной функции
( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x )
Производная неявно заданной функции
Производная обратной функции
Обратные тригонометрические функции
Производная параметрически заданной функции
y = f ( x ) y ‘ = y · ( ln ( f ( x ) ) ) ‘
Пояснения таблицы
Содержимое таблицы требует небольших пояснений. Например, в наиболее простом случае для дифференцирования нам пригодится определение производной, т.е. вычисление соответствующего предела. Это действие носит название непосредственного дифференцирования.
Если вам приходится работать с основной элементарной функцией, то следует использовать таблицу основных производных. В ней приводятся все готовые значения, доказанные на основании определения. Это очень удобно, и мы советуем вам держать такую таблицу под рукой.
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
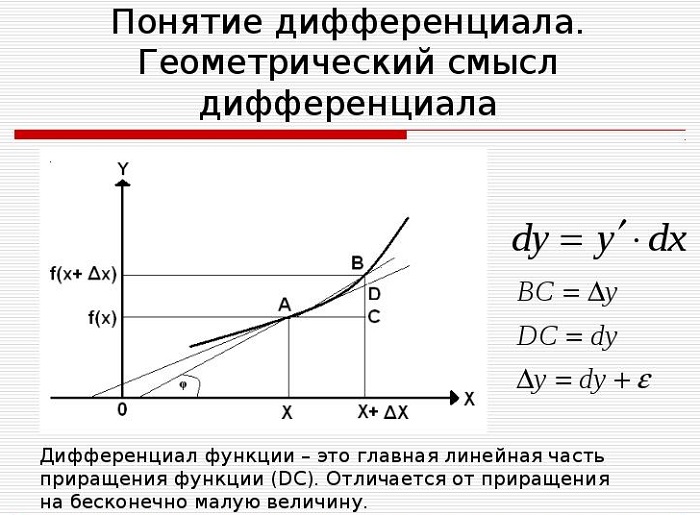
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
Отсюда получается формула:
Для второго порядка вводится обозначение d 2 y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Примеры решения задач
Задача №1
Найти дифференциал функции
Задача №2
Вычислить значение дифференциала функции
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d 2 y, если y = cos2x и x – независимая переменная.
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Заключение
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.