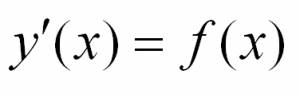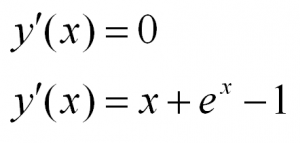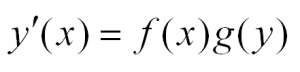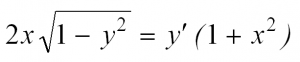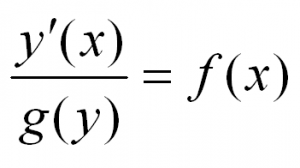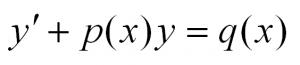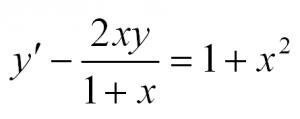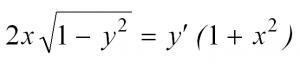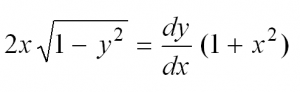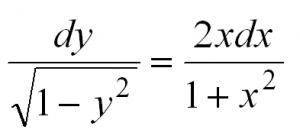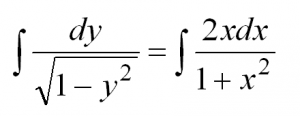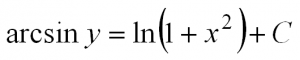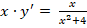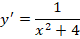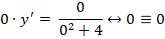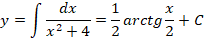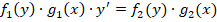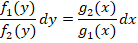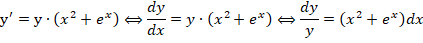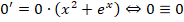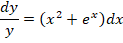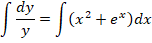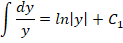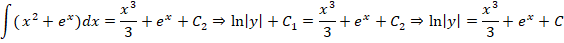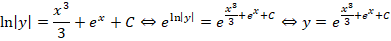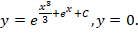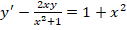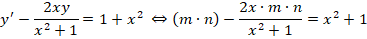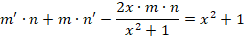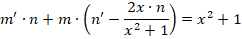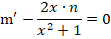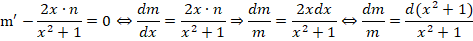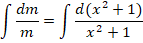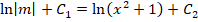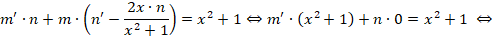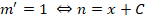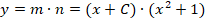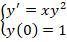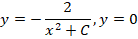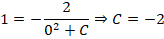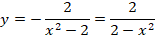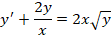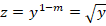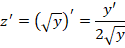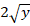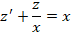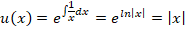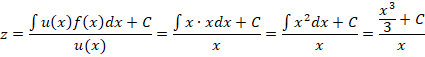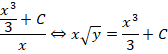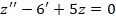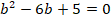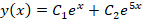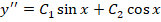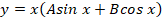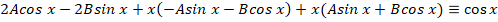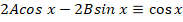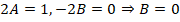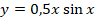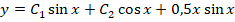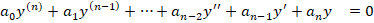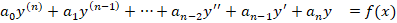что такое дифференциальные уравнения для чайников

Дифференциальные уравнения для «чайников». Примеры решения

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Решение уравнений

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Математика

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

Приведем примеры подобных дифференциальных уравнений:

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

Частные решения мы можем выбрать из систем независимых функций:

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

Источник

Многих людей, хоть как-то изучавших курс высшей математики в учебном заведении, приводит в ужас словосочетание «дифференциальные уравнения». Согласно строгому научному определению в книгах – так именуются математические выражения, где в состав входят функция, ее производная или параметр. Имеется достаточно большое количество типов этих равенств, рассмотрим подходы к их решению так, чтобы они были понятны даже для «чайников».

Дифференциальные уравнения первого порядка

Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х):

здесь, F(x,y,y ’ ) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у ’ ).Таково строгое математическое определение ДУ.

Для примера можно привести следующее уравнение:

Простейшие ДУ первого порядка

Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х.

После интегрирования получим такое выражение:

Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида:

здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа.

Задача №1

Необходимо определить все возможные варианты решения диффуравнения, имеющего вид

Последовательно рассмотрим решение.

Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее:

Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию:

Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение:

Данное выражение – это решение для приведенного диффуравнения.

ДУ с разделяющимися переменными

Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства.

Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными.

Их общий вид следующий:

После проведения нескольких преобразований, это выражение может быть сведено к следующему виду:

При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений.

Задача №2

Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x 2 + e x )

Как решать? В первую очередь проводим разделение переменных в разные части уравнения:

Данные преобразования справедливы, если у ≠ 0.

Это означает, что y = 0 – одно из возможных решений задачи.

Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения:

Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду:

Правильными решениями, в результате преобразований, будут:

Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина.

Линейные неоднородные ДУ первого порядка

Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные.

Основной принцип при нахождении решения сводится к следующим шагам:

Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению.

Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию.

На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ.

Задача №3

Рассмотрим применение методики решения на примере.

Необходимо найти решение дифференциального уравнения вида

Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается:

На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю.

Получаем дополнительное дифференциальное уравнение:

Выполняем оставшиеся преобразования:

Вполне очевидно, что ответом на условие задачи будет функция:

Задача Коши для ДУ

При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения).

На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную.

Чтобы это сделать, необходимо рассмотреть плоскость X_oy, где должна быть задана некая точка D₀, имеющая координаты (x₀, y₀) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом.

Когда мы с самого начала задаем точку D₀(x₀, y₀) – это означает, задание начального условия y(x₀) = y₀. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.

Задача №4

Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида:

Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy 2 стандартным методом. Его решение приводить не будем, приведем только ответ:

Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С:

Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений:

Полученная функция – ответ на задачу Коши в этом примере.

Дифференциальные уравнения Бернулли

ДУ Бернулли обычно представлено в следующем виде:

Обязательное условие, что функции b(x) и c(x) – являются непрерывными.

Задача №5

Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения:

Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения:

Выполним деление по начальному уравнению Бернулли на

и выполним необходимые преобразования:

Произведем замену параметра х на параметр у:

Теперь вычисляем интегрирующий модуль для данной функции, он будет равен:

Теперь производим ряд преобразований для вычисления решения диффуравнения:

Переписываем полученную функцию в неявном виде и получаем ответ:

Дифференциальные уравнения второго порядка

Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня.

Общий вид таких уравнений таков:

Линейные однородные ДУ второго порядка с постоянными коэффициентами

Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид:

При это важным условием теории является причисление r и k к действительным числам.

Задача №6

Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере.

Найти решение диффуравнения 2-го порядка вида:

Во всех таких случаях начинаем с поиска характеристического уравнения:

Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5.

Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде:

Линейные неоднородные ДУ второго порядка с постоянными коэффициентами

Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу:

Переменные r и k должны быть вещественными и постоянными числами.

Задача №7

Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x.

Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k 2 + 1 = 0.

Исходя из этого записываем решение для однородного уравнения:

Из-за отсутствия параметра с производной первого порядка также будет справедливо записать:

Теперь остается только подставить найденные выражения:

Частное и общее решение для уравнения можно записать:

Дифференциальные уравнения высших порядков

Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом:

Для неоднородных справедлив другой формат:

Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип.

Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье.

Источник