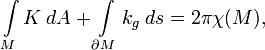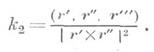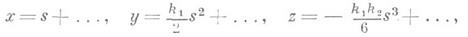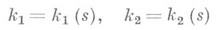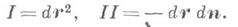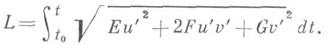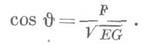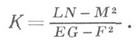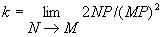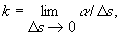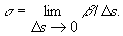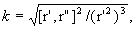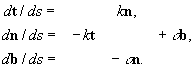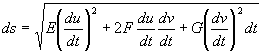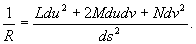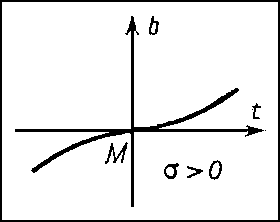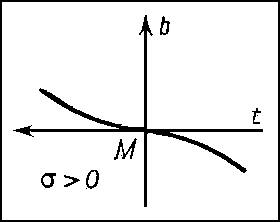что такое дифференциальная геометрия

03.12.202318.04.2022 admin 0 Comments

Дифференциальная геометрия

Дифференциальная геометрия — это один из разделов геометрии, в котором изучаются свойства кривых, поверхностей и других геометрических многообразий с помощью методов математического анализа, в частности — дифференциального исчисления.

Возникла и развивалась дифференциальная геометрия вместе с математическим анализом, который сам в действительности базируется на геометрии. основные геометрические понятия легли в основу соответствующий терминов анализа. К примеру, понятие площади и объема предшествовало понятию интеграл.

Зародилась дифференциальная геометрия в XVIII веке. Ее появление связано с именами выдающихся математиков того времени Эйлера и Монжа. Первое сводное сочинение по теории поверхностей была написано в 1795 году Монжем «Приложение анализа к геометрии».

В 1827 Гаусс опубликовал работу «Общее исследование о кривых поверхностях», в которой изложил основы теории поверхностей в её современном виде. С этого момента дифференциальная геометрия получила официальный статус самостоятельной отрасли математической науки.

Научно-исследовательские работы по дифференциальной геометрии К. Гаусса (1777-1855гг.), Г. Дарбу (1842-1917гг.), Л. Бианки (1856-1928гг.) и Л.Эйзенхарта (1876-1965гг.) были посвящены, главным образом, свойствам, проявляющимся в малой окрестности обычной точки многообразия. Предмет этих исследований стал сутью так называемой дифференциальной геометрии «в малом». Начиная с 1930-х годов, исследования математиков были направлены, прежде всего, на изучение взаимосвязей между дифференциальной геометрией малых окрестностей и «глобальными» свойствами всего многообразия. Эта теорию получила название дифференциальной геометрией «в целом».

Важную роль в развитии геометрии, и дифференциальной геометрии, в частности, сыграло открытие неевклидовой геометрии. В лекции «О гипотезах, лежащих в основаниях геометрии», прочитанной Риманом в 1854 году, были сформулированы основы новой геометрии. впоследствии эта геометрия стала носить имя своего создателя. Сегодня риманова геометрия является наиболее развитой частью дифференциальной геометрии.

В «Эрлангенской программе» 1872 года Клейн изложил теоретико-групповую точку зрения на геометрию. Согласно Клейну, геометрия — это учение об инвариантах (то есть об неизменных величинах) групп преобразований. Применительно к дифференциальной геометрии это учение было развито Картаном, который создал теорию пространственно-проективной и аффинной (родственной) связности.

Следует отметить, что дифференциальная геометрия и топология являются смежными разделами математики. Однако топология значительно более молодой раздел, который начал развиваться лишь в начале XX века.

Наиболее фундаментальная из известных взаимосвязей между топологией и дифференциальной геометрией устанавливается теоремой Гаусса — Бонне, которая утверждает, что для обычных замкнутых поверхностей

Надо сказать, что дифференциальная геометрия также как и вся геометрия подразделяется на несколько основных отраслей. К ним относятся:

Первоначально дифференциальная геометрия занималась изучением свойств кривых поверхностей в обычном пространстве, в настоящее время в область ее изучения вошли многообразия любого числа измерений, которые могут быть, а могут и не быть подпространствами евклидова пространства.

Источник

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ

— раздел геометрии, в к-ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в Д. г. изучаются свойства семейств линий и поверхностей (см., напр., Конгруэнция, Сеть).

Возникновение Д. г. относится к 18 в. и связано с именами Л. Эйлера (L. Euler) и Г. Монжа (G. Monge). Первое сводное сочинение по теории поверхностей написано Г. Монжем (Приложение анализа к геометрии, 1795). В 1827 К. Гаусс (С. Gauss) опубликовал работу «Общее исследование о кривых поверхностях», в к-рой заложил основы теории поверхностей в ее современном виде. С тех пор Д. г. перестала быть только приложением анализа и заняла самостоятельное место в математике.

Открытие в 1826 Н. И. Лобачевским неевклидовой геометрии сыграло огромную роль в развитии всей геометрии, в том. 1, если при где д(Х)- расстояние точки Xмножества Мот т. Если в качестве Мвзять кривую, а в качестве тпрямую, проходящую через точку Окривой, то при условие соприкосновения определяет касательную к кривой в точке О(рис. 1).

Гладкая (дифференцируемая) кривая в каждой точке имеет определенную касательную. Направление касательной в точке t₀ кривой, задаваемой уравнениями (1), совпадает с направлением вектора [ х’(t₀), у’(t₀), z(t₀)]. В Д. г. выводятся уравнения касательной для различных способов аналитич. адания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t₀, будут

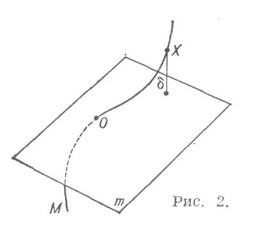
где индекс ₀ указывает на значение функций х, у, z и их производных в точке t₀. Если взять в качестве тплоскость, проходящую через точку Окривой М, то условие соприкосновения при 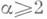определяет соприкасающуюся плоскость кривой (рис. 2).

Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая череа касательную кривой, является соприкасающейся.

При движения вдоль кривой ее касательная вращается. Скорость этого вращения при равномерном, с единичной скоростью, движении вдоль кривой наз. кривизной кривой. В случае параметрич. задания кривой уравнениями (1) кривизна кривой определяется по формуле где r(t)- вектор-функция с координатами x(t), y(t), z). Прямые и только прямые имеют всюду равную нулю кривизну. Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость. При движении вдоль кривой в окрестности такой точки соприкасающаяся плоскость вращается, причем касательная кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении вдоль кривой наз. кручением кривой. В зависимости от направления вращения определяется знак кручения. Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определенное кручение. В случае параметрич. задания кривой уравнениями (1) кручение кривой определяется по формуле

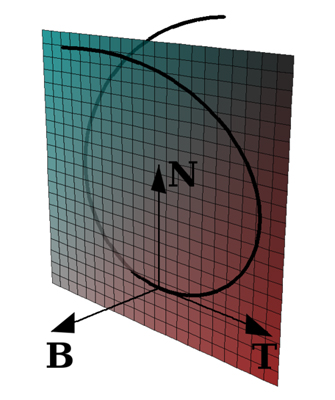
Прямая, перпендикулярная касательной, проходящая через точку касания, наз. нормалью к кривой. Нормаль, лежащую в соприкасающейся плоскости, наз. главной нормалью, а нормаль, перпендикулярную соприкасающейся плоскости, наз. бинормалью. Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, наз. естественным трехгранником (трехгранником Френе). Если ребра естественного трехгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации имеет в окрестности этой точки вид

где k₁ и k₂ — кривизна и кручение кривой в указанной точке. На рис. 3 изображены проекции кривой на грани естественного трехгранника вблизи точки с отличными от нуля кривизной и кручением.

Единичные векторы t, v, b касательной, главной нормали и бинормали кривой при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы

где штрихом обозначено дифференцирование по дуге кривой. Формулы (2) наз. Френе формулами. Кривая с отличной от нуля кривизной определяется с точностью до положения в пространстве заданием ее кривизны и кручения в функции дуги sкривой. В связи с этим систему уравнений

наз. натуральными уравнениями кривой.

Важный класс кривых представляют плоские кривые, т. 2 с поверхностью в этой точке. В каждой точке дважды дифференцируемой поверхности существует единственный соприкасающийся параболоид, к-рый может вырождаться в параболич. цилиндр или плоскость. 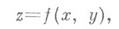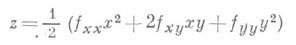Если поверхность отнести к прямоугольным декартовым координатам, приняв данную точку поверхности за начало координат, а касательную плоскость в ней за плоскость ху, то уравнение поверхности в окрестности точки касания будет а уравнение соприкасающегося параболоида в этой точке (производные функции f берутся в точке касания). В зависимости от вида соприкасающегося параболоида точки поверхности подразделяются на эллиптические точки, гиперболические точки, параболические точки и уплощения точки. Значение соприкасающегося параболоида состоит в том, что он воспроизводит форму поверхности с точностью до бесконечно малых 2-го порядка (касательная плоскость воспроизводит ее форму с точностью до бесконечно малых 1-го порядка).

С помощью соприкасающегося параболоида вводится понятие сопряженных направлений на поверхности. Именно два направления на поверхности в данной точке наз. сопряженными, если содержащие их прямые сопряжены относительно соприкасающегося параболоида в этой точке. Ортогональные сопряженные направления наз. главными. В данной точке поверхности, как правило, два главных направления. Исключение составляют точки уплощения и специальные эллиптич. течки ( округления точки), в к-рых каждое направление главное. Линия, у к-рой в каждой точке направление является главным, наз. кривизны линией. В точках поверхности, не являющихся эллиптическими, существуют самосопряженные направления. Они наз. асимптотическими направлениями. Линия на поверхности, направление к-рой в каждой точке асимптотическое, наз. асимптотической линией.

Подобно тому, как для семейства кривых на плоскости, вводится понятие огибающей семейства поверхностей. При этом семейство поверхностей может быть однопараметрическим или двухпараметрическим. В теории поверхностей особое значение имеет огибающая однопараметрич. семейства плоскостей.

В теории поверхностей важную роль играют две дифференциальные квадратичные формы поверхности, связанные с поверхностью. Если через r(u, v )обозначить вектор точки на поверхности, а через ( и, v )единичный вектор нормали к поверхности, то эти квадратичные формы записываются в виде

Коэффициенты первой и второй квадратичных форм обычно обозначаются Е, 2F, G и L, 2M, N соответственно. Первая из этих форм дает расстояние на поверхности между точкой (и, v)и бесконечно близкой точкой (u+du,u+du):

Длина кривой, задаваемой на поверхности уравнениями u=u(t), v=v(t), вычисляется при помощи первой квадратичной формы

Первая квадратичная форма, поверхности определяет углы между кривыми на поверхности. В частности, для угла J между координатными линиями u=const, u=const в точке их пересечения имеет место формула

Отсюда видно, что координатная сеть на поверхности ортогональна, если F=0. Площадь поверхности также определяется первой квадратичной формой и для области W на поверхности вычисляется по формуле

Вторая квадратичная форма характеризует искривленность поверхности в пространстве. Именно, отношение второй квадратичной формы к первой

представляет собой кривизну плоского сечения, нормального к поверхности, проведенного в направлении du: dv (см. Нормальная кривизна поверхности). Существует простая связь между кривизной кривой, лежащей на поверхности, и кривизной нормального сечения поверхности, проведенного через касательную кривой ( Менъе теорема). Экстремальные значения нормальной кривизны поверхности в данной точке наз. главными кривизнами. Они достигаются по главным направлениям. Нормальная кривизна поверхности в произвольном направлении выражается через главные кривизны и углы, к-рые это направление образует с главными (Эйлера формула). Главные кривизны k₁ и k₂ определяются из уравнения

Из этой формулы видно, что гауссова кривизна поверхности выражается через коэффициенты первой и второй квадратичных форм. Однако гауссову кривизну можно выразить через коэффициенты только первой формы и их производные (Гаусса теорема).

Две поверхности, между к-рыми может быть установлен гомеоморфизм, сохраняющий длины кривых, наз. изометричными поверхностями.

Коэффициенты первой и второй квадратичных форм независимы. Одно из соотношений между этими коэффициентами дает теорема Гаусса. Существуют еще два соотношения, открытые К. М. Петерсоном и Д. Кодацци (D. Codazzi) (см. Петерсона— Кодацци уравнения). Эти три соотношения составляют полную систему независимых соотношений между коэффициентами первой и второй квадратичных форм поверхности. Согласно Бонне теореме, если для двух дифференциальных квадратичных форм, из к-рых первая положительно определенная, выполнены соотношения Гаусса, Петерсона, Кодацци, то существует, и притом единственная, с точностью до положения в пространстве, поверхность, имеющая эти формы первой и соответственно второй квадратичными формами.

Источник

Дифференциальная геометрия

Раздел геометрии, в котором геометрические образы изучаются методами математического анализа. Главными объектами Д. г. являются произвольные достаточно гладкие кривые (линии) и поверхности евклидова пространства, а также семейства линий и поверхностей. Обычно в Д. г. исследуются локальные свойства геометрических образов, которые присущи сколь угодно малой их части. Рассматриваются также и свойства геометрических образов в целом (например, свойства замкнутых выпуклых поверхностей).

Геометрические объекты, изучаемые в Д. г., обычно подчинены некоторым требованиям гладкости. Как правило, эти требования выражаются в том, что функции, задающие указанные объекты, не менее двух раз непрерывно дифференцируемы.

Сущность методов Д. г., применяемых для выяснения локальных свойств геометрических объектов, проще всего уяснить на примере локального исследования формы кривых.

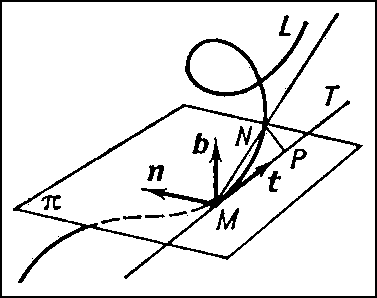
В каждой точке М достаточно гладкой кривой L можно построить касательную (См. Касательная) прямую МТ и соприкасающуюся плоскость (См. Соприкасающаяся плоскость) π (рис. 1). При этом касательная МТ является пределом секущей MN при неограниченном приближении точки N к М по кривой L, а соприкасающаяся плоскость есть предел переменной плоскости, проходящей через касательную МТ и точку N при приближении N к М по L. Касательную МТ можно рассматривать также как прямую, наиболее тесно прилегающую к L вблизи точки М. Соприкасающаяся же плоскость представляет собой плоскость, наиболее тесно прилегающую к L вблизи М.

Для геометрической характеристики искривлённости кривой L вблизи данной точки М рассматривается Соприкасающаяся окружность, представляющая собой окружность, проходящую через М и наиболее тесно прилегающую к L вблизи М. Это свойство выражается в том, что если учитывать величины только 1-го и 2-го порядка малости по сравнению с длиной дуги MN, то участок кривой L вблизи М можно считать дугой соприкасающейся окружности. Соприкасающаяся окружность касается L в точке М и расположена в соприкасающейся плоскости. Её центр называется центром кривизны кривой L в точке М, а радиус — радиусом кривизны L в М.

Для численной характеристики искривлённости L в точке М используется Кривизна k кривой, равная обратной величине радиуса R соприкасающейся окружности: k = 1/R. Кривизну k можно рассматривать и как меру отклонения L от касательной МТ (рис. 1):

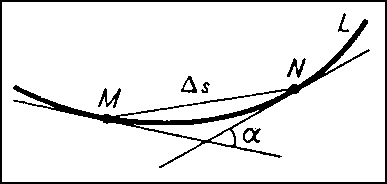
или как скорость изменения (вращения) касательной к L (рис. 2):

где α — угол между касательными в точках М и N, а Δs — длина дуги MN.

Мерой отклонения кривой от соприкасающейся плоскости π в точке М служит так называемое Кручение σ, которое определяется как предел отношения угла β между соприкасающимися плоскостями в точках М и N к длине Δs дуги MN при Δs → 0:

При этом угол β берётся со знаком +, если для наблюдателя в М вращение соприкасающейся плоскости в N при приближении N к М происходит против часовой стрелки, и со знаком — в противном случае. Кручение кривой можно рассматривать как скорость изменения (вращения) соприкасающейся плоскости. В частности, для плоской кривой соприкасающаяся плоскость во всех точках совпадает с плоскостью кривой и поэтому кручение такой кривой во всех точках равно нулю. Кривизна k и кручение σ достаточно гладкой кривой L определены в каждой её точке и представляют собой функции параметра, определяющего точки этой кривой. Для вычисления k и σ используется какой-либо способ задания кривой. Чаще всего кривая L задаётся параметрическими уравнениями в прямоугольных координатах:

При изменении параметра t точка М с координатами (x, у, z) описывает кривую L. Иными словами, параметрические уравнения кривой связаны с представлением о кривой как траектории движущейся точки. Правые части (1) могут рассматриваться и как проекции на оси координат радиуса-вектора r переменной точки М кривой L. Вектор r’ с координатами <φ'(t), ψ'(t), χ'(t)> называется производной вектор-функции r (t) и направлен по касательной к L в точке М.

Кривизна и кручение вычисляются по формулам

С каждой точкой М кривой L связаны три единичных вектора: касательной (t), главной нормали (n) и бинормали (b) (рис. 1). При этом вектор (n) расположен в соприкасающейся плоскости и направлен от точки М к центру кривизны L в М, а вектор b ортогонален t и n и направлен так, что векторы t, n и b образуют правую тройку. Указанная тройка векторов образует так называемый основной, или сопровождающий, триедр кривой L. Плоскости векторов (n, b) и (t, b) называются соответственно нормальной и спрямляющей плоскостями L в М.

Формулы для производных векторов t, n, b по длине s дуги L называются формулами Френе. Они играют фундаментальную роль как в теории кривых, так и в приложениях этой теории (в механике, теоретической физике и т.д.). Эти формулы имеют вид

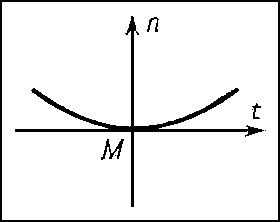
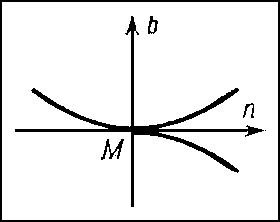
Если кривизна и кручение не равны нулю в точке М, то можно сделать определённые заключения о форме L вблизи М: проекции L на соприкасающуюся и нормальную плоскости в М имеют вид, изображённый соответственно на рис. 3 и 4. Форма проекции на спрямляющую плоскость зависит от знака кручения. На рис. 5 и 6 изображены проекции L на спрямляющую плоскость для σ > 0 и σ

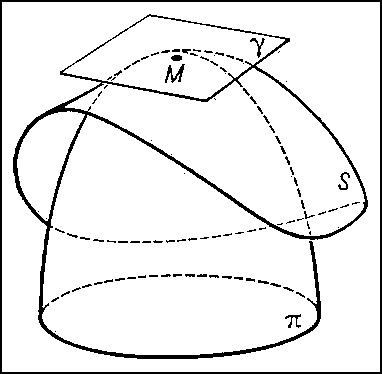
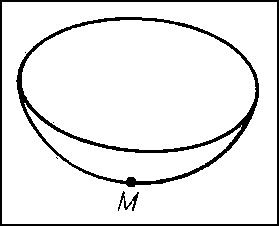
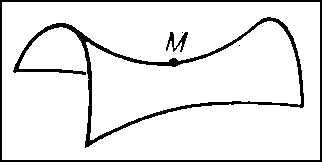
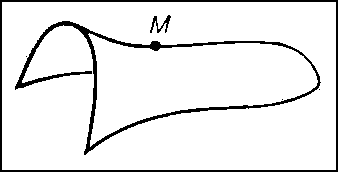
По аналогии с кривыми исследуется локальное строение формы поверхностей. В каждой точке М достаточно гладкой поверхности S можно построить касательную плоскость (См. Касательная плоскость) γ и однозначно определённый соприкасающийся параболоид π (рис. 7), который может выродиться в параболический цилиндр или плоскость. При этом касательную плоскость можно рассматривать как плоскость, наиболее тесно прилегающую к S вблизи М. Соприкасающийся же параболоид характеризуется тем, что в окрестности точки М он совпадает с S с точностью до величин третьего порядка малости по сравнению с размерами этой окрестности. С помощью соприкасающихся параболоидов точки М поверхностей классифицируются следующим образом: эллиптическая (рис. 8) (соприкасающийся параболоид — эллиптический), гиперболическая (рис. 9) (соприкасающийся параболоид — гиперболический), параболическая (рис. 10) (соприкасающийся параболоид — параболический цилиндр), точка уплощения (рис. 11) (соприкасающийся параболоид — плоскость).

Обычно для исследования строения поверхности используются так называемая первая и вторая основные квадратичные формы поверхности.

Пусть поверхность S определена параметрическими уравнениями:

При фиксированном значении v уравнения (2) определяют на S линию, называемую координатной линией u. Аналогично определяется линия v. Координатные линии u и v образуют на S параметрическую сеть (если, например, сферу радиуса 1 задать параметрическими уравнениями

то параметрической сетью линий u и v будут меридианы и параллели этой сферы). Величины u и v называются также внутренними координатами, т.к. точка на поверхности есть точка пересечения проходящих через неё координатных линий, т. е. может быть найдена путём построений на поверхности без обращения к объемлющему пространству.

Радиус-вектор r произвольной точки М на S определяется уравнениями (2) как функция u и v. Частные производные r_u и r_v этой функции суть векторы, касательные соответственно к линиям u и v. Эти векторы в точке М лежат в касательной плоскости к S в М. Векторное произведение [r_u, r_v] определяет нормаль к S в точке М.

Правая часть соотношения (3) называется первой основной квадратичной формой поверхности S. С помощью этой формы можно измерять длины дуг на поверхности путём интегрирования выражения

вдоль рассматриваемой дуги. Поэтому форма (3) называется также метрической формой поверхности. Первая форма определяет также внутреннюю геометрию (См. Внутренняя геометрия) поверхности, т. е. совокупность фактов, которые могут быть получены путём измерений на поверхности, без обращения к объемлющему пространству. Внутренняя геометрия поверхности не меняется при её изгибании — деформации поверхности как абсолютно гибкой и нерастяжимой плёнки.

Вторая основная квадратичная форма поверхности представляет собой выражение

в котором L = r_uun, М = r_uvn, N = r_vvn (n — единичный вектор нормали к S в точке М). С помощью второй формы можно получить представление о пространственной форме поверхности. Например, кривизны 1/R нормальных сечений поверхности в данной точке М (т. е. линий пересечения S с плоскостями, проходящими через нормаль в М) вычисляются по формуле

Две основные формы поверхности, заданные в каких-либо внутренних координатах, определяют поверхность с точностью до положения в пространстве. Если заданы две формы

первая из которых положительная, а коэффициенты L, M и N второй удовлетворяют некоторой системе уравнений, из которых одно (полученное К. Гауссом) алгебраическое, а два других (полученные К. М. Петерсоном) — линейные дифференциальные уравнения с частными производными первого порядка, то найдётся поверхность, для которой эти формы являются соответственно первой и второй основными формами.

Отмеченные уравнения Гаусса — Петерсона играют фундаментальную роль в теории поверхностей.

Подробнее о поверхностях см. Поверхностей теория.

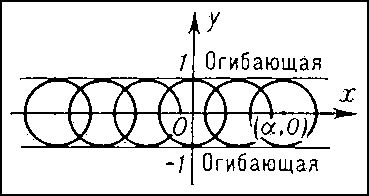
Одним из объектов исследований в Д. г. являются семейства кривых и поверхностей. Такие семейства задаются посредством уравнений, содержащих параметры. Например, уравнение (х — α) 2 + у 2 = 1, содержащее параметр α, определяет семейство окружностей радиуса 1 с центрами в точках (α, 0), т. е. на оси Ox (рис. 12). С семейством кривых (поверхностей) связано понятие огибающей — такой кривой (поверхности), которая касается всех кривых (поверхностей) семейства. В рассмотренном выше примере огибающей будет пара параллельных оси Ox прямых, отстоящих от неё на расстоянии 1. Особенно детально в Д. г. исследованы двупараметрические семейства прямых b в пространстве, называемые конгруэнциями. Простейший пример конгруэнции — семейство параллельных прямых в пространстве. Истоком теории конгруэнций является геометрическая оптика.

Различные разделы Д. г. посвящены изучению во всевозможных аспектах так называемых дифференциально-геометрических многообразии (См. Многообразие). Примерами таких многообразий могут служить кривые (одномерные многообразия), поверхности (двумерные многообразия), обычное евклидово пространство (трёхмерное многообразие). Более сложным примером может служить четырёхмерное многообразие, элементами которого являются прямые обычного евклидова пространства (прямая в декартовых координатах определяется уравнениями вида z = ax + b, z = су + d; числа a, b, с, d можно рассматривать как координаты этой прямой).

Изучение дифференциально-геометрических многообразий ведётся по следующим основным направлениям. 1) Геометрия транзитивной группы отображений многообразия на себя, или геометрия «локальной группы» отображений. В тематику этих вопросов входят обычная классическая локальная Д. г. (изучение инвариантов группы движений евклидова пространства), аффинная, проективная и конформная геометрии (изучение инвариантов соответствующей группы преобразований). 2) Геометрия многообразий с римановой метрикой (римановых пространств (См. Риманово пространство)), представляющая собой обобщение на многомерный случай внутренней геометрии поверхностей, которое можно рассматривать как двумерные римановы пространства. Геометрия римановых пространств играет важную роль в теории относительности. 3) Геометрия так называемых финслеровых пространств, являющихся обобщением римановых пространств. 4) Геометрия многообразий со связностью, т. е. многообразий, в которых указан способ, с помощью которого можно сравнивать геометрические образы, расположенные в касательных пространствах в разных точках.

Возникновение Д. г. связано с именами Л. Эйлера и Г. Монжа. Ими к концу 18 в. были получены важные факты теории поверхностей. Значительный вклад в развитие Д. г. сделан в начале 19 в. К. Гауссом, который ввёл обе основные квадратичные формы. Им же была доказана теорема об инвариантности полной кривизны относительно изометрических преобразований. Фактически им были заложены основы внутренней геометрии поверхностей. Построение основ классической теории поверхностей было завершено в середине 19 в. основателем московской геометрической школы К. М. Петерсоном. В середине и во 2-й половине 19 в. много глубоких и общих результатов по классической теории поверхностей было получено Ф. Миндингом, Ж. Лиувиллем (См. Лиувилль), Э. Бельтрами, Ж. Г. Дарбу, Л. Бианки. Ряд замечательных результатов по классической Д. г. был получен русскими учёными Д. Ф. Егоровым, Н. Н. Лузиным, С. П. Финиковым и др.

Развитие др. направлений в Д. г. связано с именами Б. Римана, Г. Ламе, Ф. Клейна, Г. Вейля (См. Вейль), Э. Картана.

В СССР разрабатывались различные направления Д. г.; наибольшие успехи относятся к области проблем «в целом» (А. Д. Александров, А. В. Погорелов и др.).

Лит.: Монж Г., Приложение анализа к геометрии, пер. с франц., М. — Л., 1936; Стройк Д. Дж., Очерк истории дифференциальной геометрии до XX столетия, пер. с англ., М. — Л., 1941; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Рашевский П. К., Курс дифференциальной геометрии, 3 изд., М., 1950; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; Рашевский П. К., Риманова геометрия и тензорный анализ, 2 изд., М., 1964; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969.