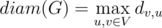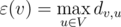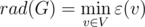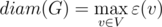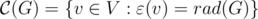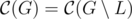что такое диаметр графа

Теория графов — Основные свойства

Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.

Расстояние между двумя вершинами

Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.

Обозначение — d (U, V)

Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.

пример

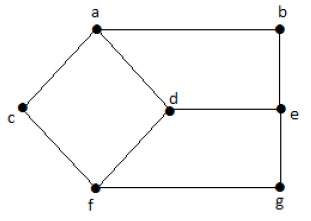
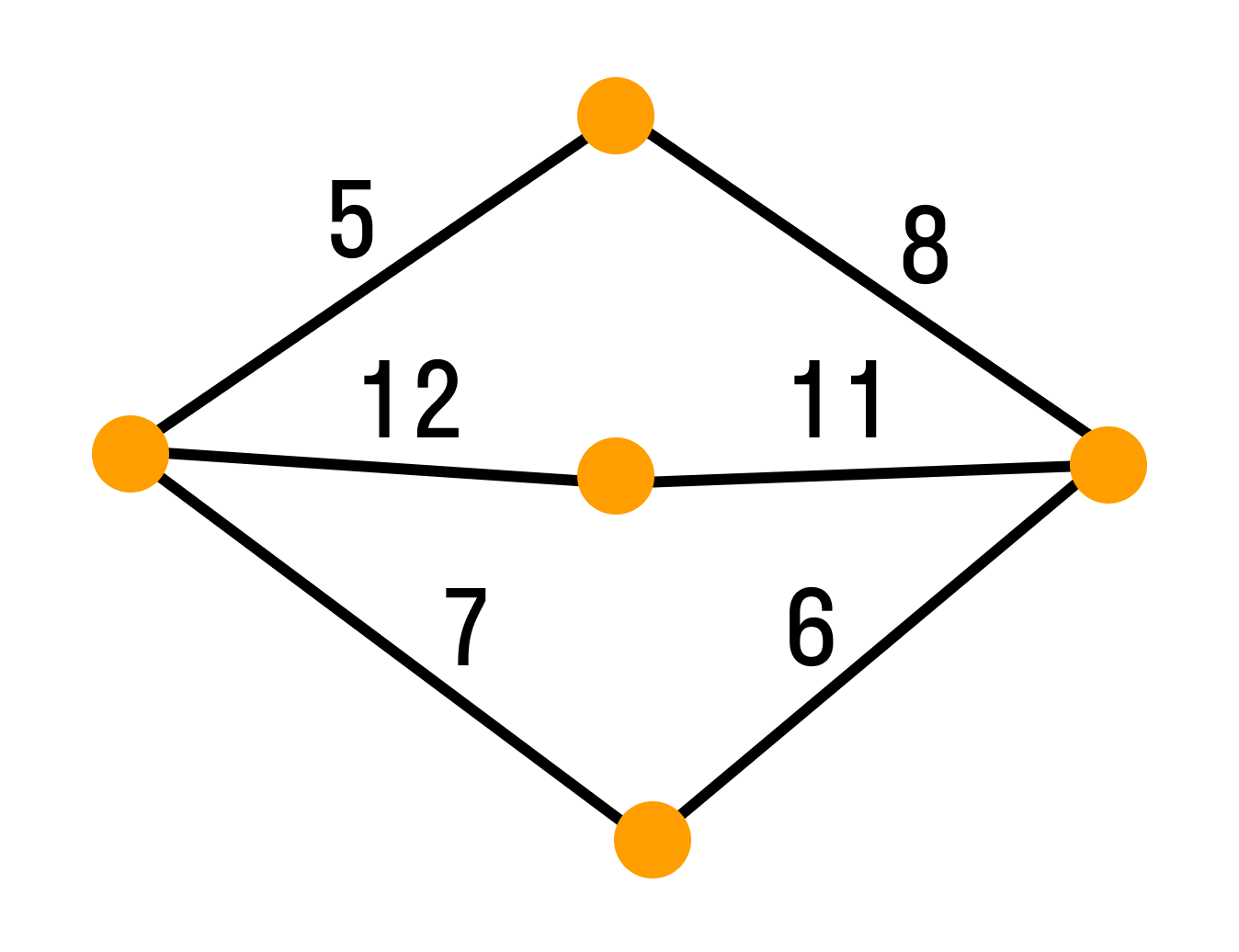
Посмотрите на следующий график —

Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ —

Эксцентриситет вершины

Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.

Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.

пример

На приведенном выше графике эксцентриситет «а» равен 3.

Расстояние от «a» до «b» равно 1 («ab»),

от ‘a’ до ‘c’ равно 1 (‘ac’),

от «а» до «d» равно 1 («объявление»),

от ‘a’ до ‘e’ равно 2 (‘ab’ — ‘be’) или (‘ad’ — ‘de’),

от ‘a’ до ‘f’ равно 2 (‘ac’ — ‘cf’) или (‘ad’ — ‘df’),

от ‘a’ до ‘g’ равно 3 (‘ac’ — ‘cf’ — ‘fg’) или (‘ad’ — ‘df’ — ‘fg’).

Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.

Радиус связного графа

Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.

Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.

Пример — На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».

Диаметр графика

Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.

Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.

Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.

Центральная точка

Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если

тогда «V» является центральной точкой графа «G».

Пример — в примере графика ‘d’ является центральной точкой графика.

Центр

Множество всех центральных точек «G» называется центром графа.

Пример. В примере графика <‘d’>является центром графика.

Длина окружности

Число ребер в самом длинном цикле «G» называется окружностью «G».

Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.

обхват

Число ребер в кратчайшем цикле G называется его обхват.

Пример — в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.

Теорема о сумме степеней вершин

Следствие 1

Следствие 2

В любом неориентированном графе число вершин с нечетной степенью является четным.

Следствие 3

В неориентированном графе, если степень каждой вершины равна k, то

Следствие 4

В неориентированном графе, если степень каждой вершины не меньше k, то

Следствие 5

В неориентированном графе, если степень каждой вершины не более k, то

Источник

Электронная библиотека

Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).

Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:

Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.

Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.

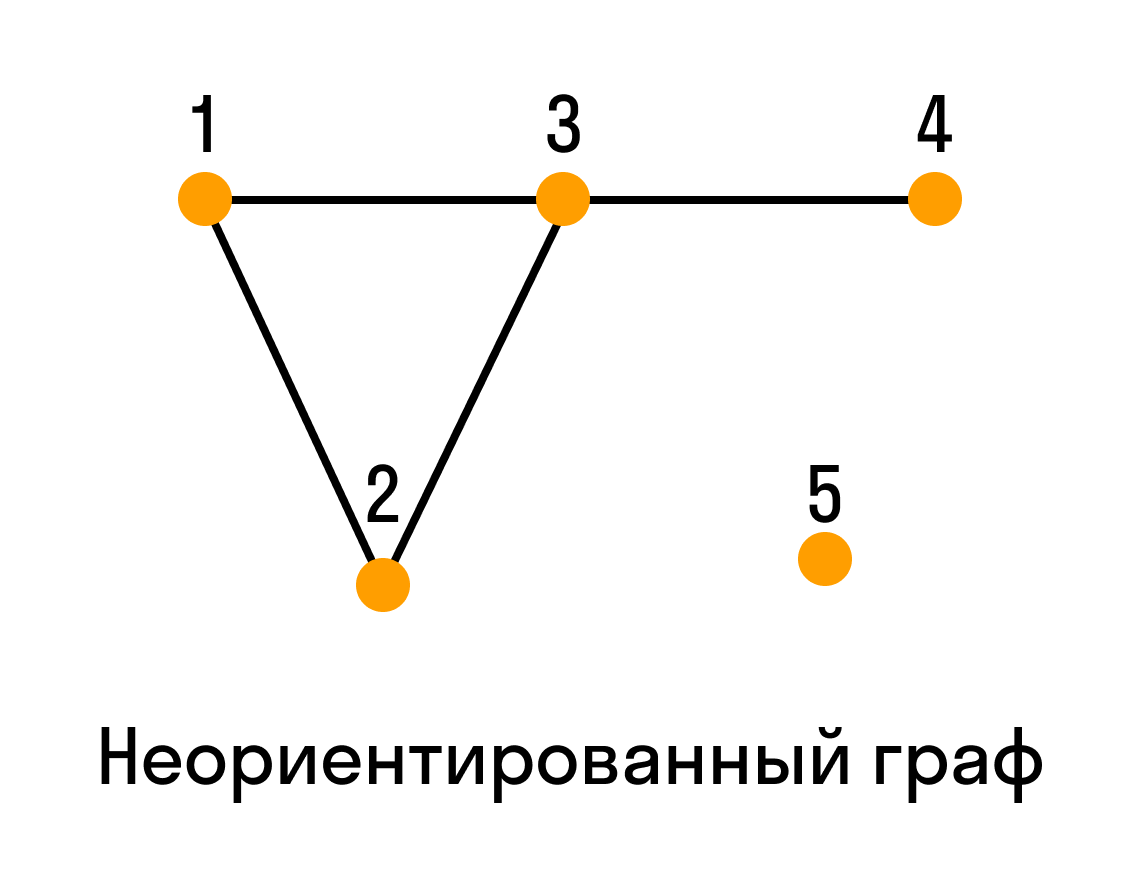
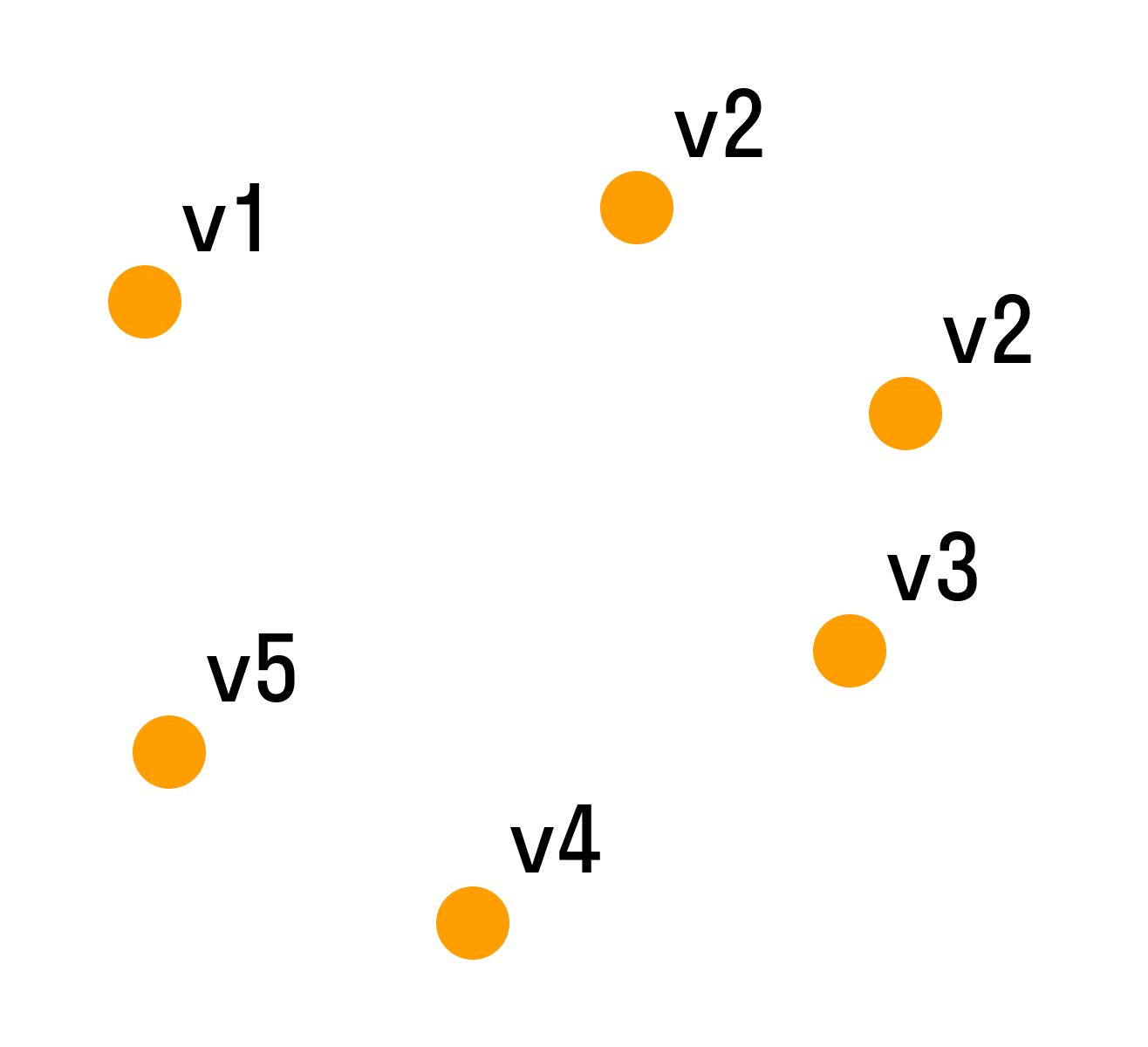
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.

Рис. 3.16. Граф для примера 82

Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами d_ij которой будут расстояния между вершинами v_i и v_j. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.

С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: для i, j = 1, 2, …, 5. В результате получаем: r(v₁) = 3, r(v₂) = 2, r(v₃) = 2, r(v₄) = 2, r(v₅) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v₂, v₃, v₄.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник

Что такое диаметр графа

Центр графа и его нахождение

Время от времени на CodeForces появляются вопросы о центре, радиусе и диаметре графа (смог нагуглить только о дереве, хотя было больше). В этом топике даны определения этим понятиям а также описаны алгоритмы для их нахождения.

Определим d i, j как кратчайшее расстояние между парой вершин . Тогда диаметр графа определяется как максимально возможное среди всех кратчайших расстояний между парой вершин: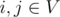

Также введем понятие эксцентриситета вершины как максимальное расстояние от вершины до какой-либо другой:

Зная эксцентриситет всех вершин, можно определить и радиус графа, как минимальный из них:

Сразу можно заметить, что диаметр графа это максимальный эксцентриситет в графе, т.е:

Центром графа назовем все вершины с эксцентриситетом, равным радиусу графа:

Определения даны и в голову приходит тривиальный алгоритм для нахождения центра, радиуса и диаметра для произвольного графа при помощи алгоритма Флойда-Уоршелла:

Теперь немного изменим постановку задачи: допустим, что граф G является деревом. Для дерева несложно доказать следующий факт: количество вершин в центре дерева равно одному или двум.

Эта теорема приводит нас к следующему алгоритму: будем удалять листья дерева, слой за слоем, пока не останется ≤ 2 вершин. Эти вершины и будут центром графа. Реализация данного алгоритма очень похожа на поиск в ширину:

Задачек на порешать сходу не нашел, так что если знаете — ждем в комментах.

Спасибо за внимание, насчет опечаток просьба писать в личку.

Источник

Тема 7. Маршруты. Расстояние между вершинами графа. Диаметр и центр графа

Пусть G – конечный н-граф.

Маршрутом в G называется последовательность ребер, в которой каждые два соседних ребра имеют общую вершину:

.

Число ребер в маршруте называется его длиной.

Маршрут М называется маршрутом общего вида, если вершины и ребра повторяются, цепью – если его ребра не повторяются, простой цепью – если его вершины не повторяются,

Маршрут, в котором совпадают начальная и конечная вершины, т.е. , называется циклическим (замкнутым).

Циклический маршрут М называется маршрутом общего вида, если вершины и ребра повторяются, циклом – если его ребра не повторяются, простым циклом – если его вершины не повторяются (кроме начала и конца).

Граф, не содержащий циклов, называется ациклическим.

Вершины и называются связными, если существует маршрут с началом в и концом в .

Утверждение: Отношение связности вершин графа является отношением эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества .

Граф называется связным, если для любых двух различных вершин существует маршрут, соединяющий их.

Очевидно, что все подграфы G(V_i) этого графа связны и называются связными компонентами графа.

Расстоянием между вершинами a и b называется длина минимальной простой цепи, связывающей их. Расстояние обозначается d(a, b).

Матрица расстояний, это симметричная квадратная матрица размерности , строки и столбцы которой соответствуют вершинам графа, а на пересечении строк и столбцов записано расстояние между вершинами .

		…
			…
			…
…	…	…	…	…	…
			…

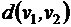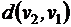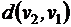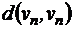В последнем столбце матрицы указан эксцентриситет для каждой вершины: расстояние от данной вершины до наиболее удаленной вершины.

. (7.1)

Диаметр графа G – максимальное расстояние между вершинами графа. Диаметр находится по формуле:

.

Используя найденные эксцентриситеты вершин, диаметр можно найти по формуле:

. (7.2)

Радиус графа G – минимальное значение эксцентриситета. Радиус находится по формуле:

. (7.3)

Центрграфа G – такая вершина, для которой .

Замечание. Центр в графе может быть не единственный.

Диаметральная цепь графа G – простая цепь, длина которой равна диаметру, соединяющая наиболее удаленные вершины графа.

Радиальная цепь графа G – простая цепь, длина которой равна радиусу, соединяющая центр и наиболее удаленную от него вершину графа.

Пример 7.1.

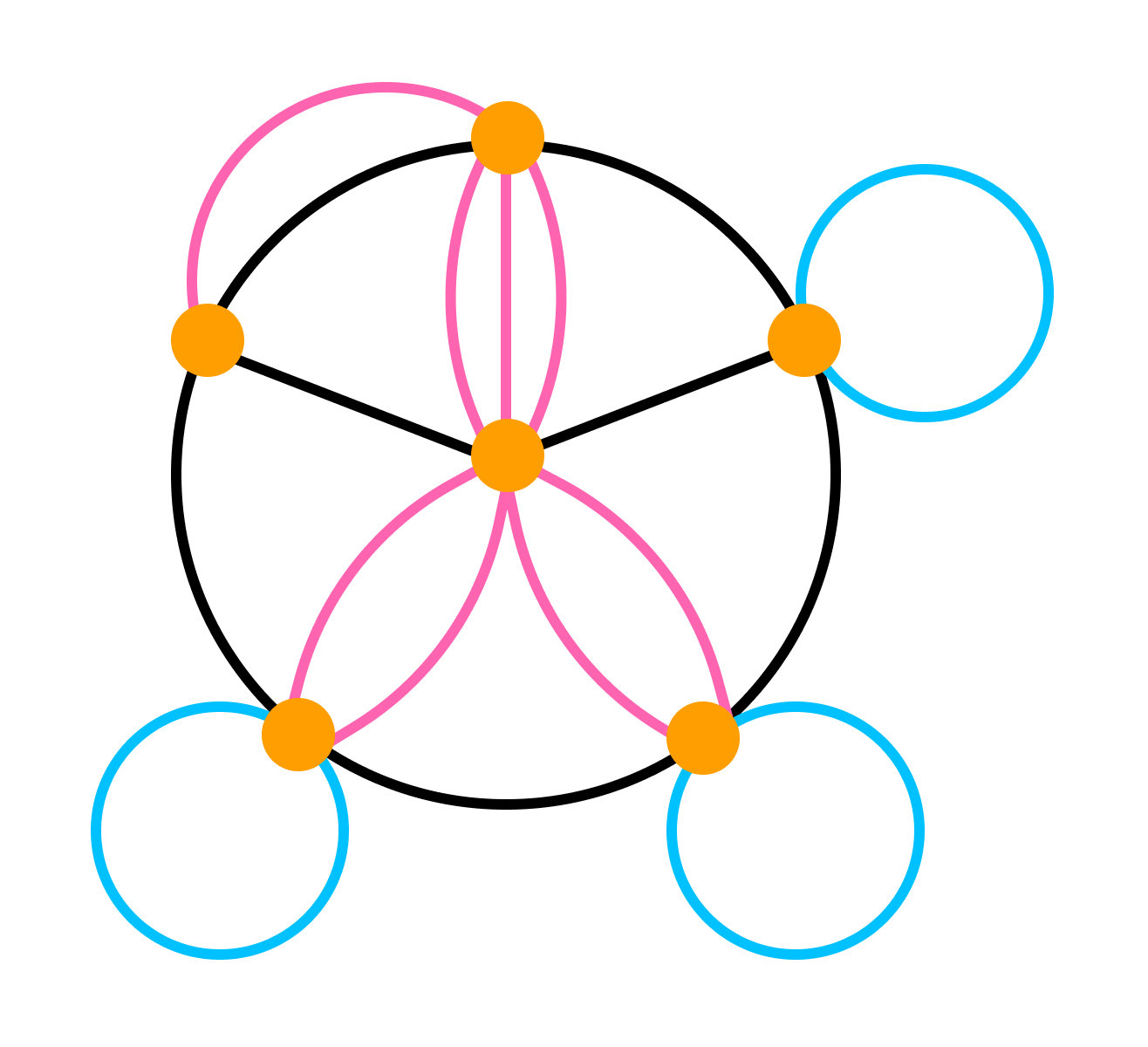
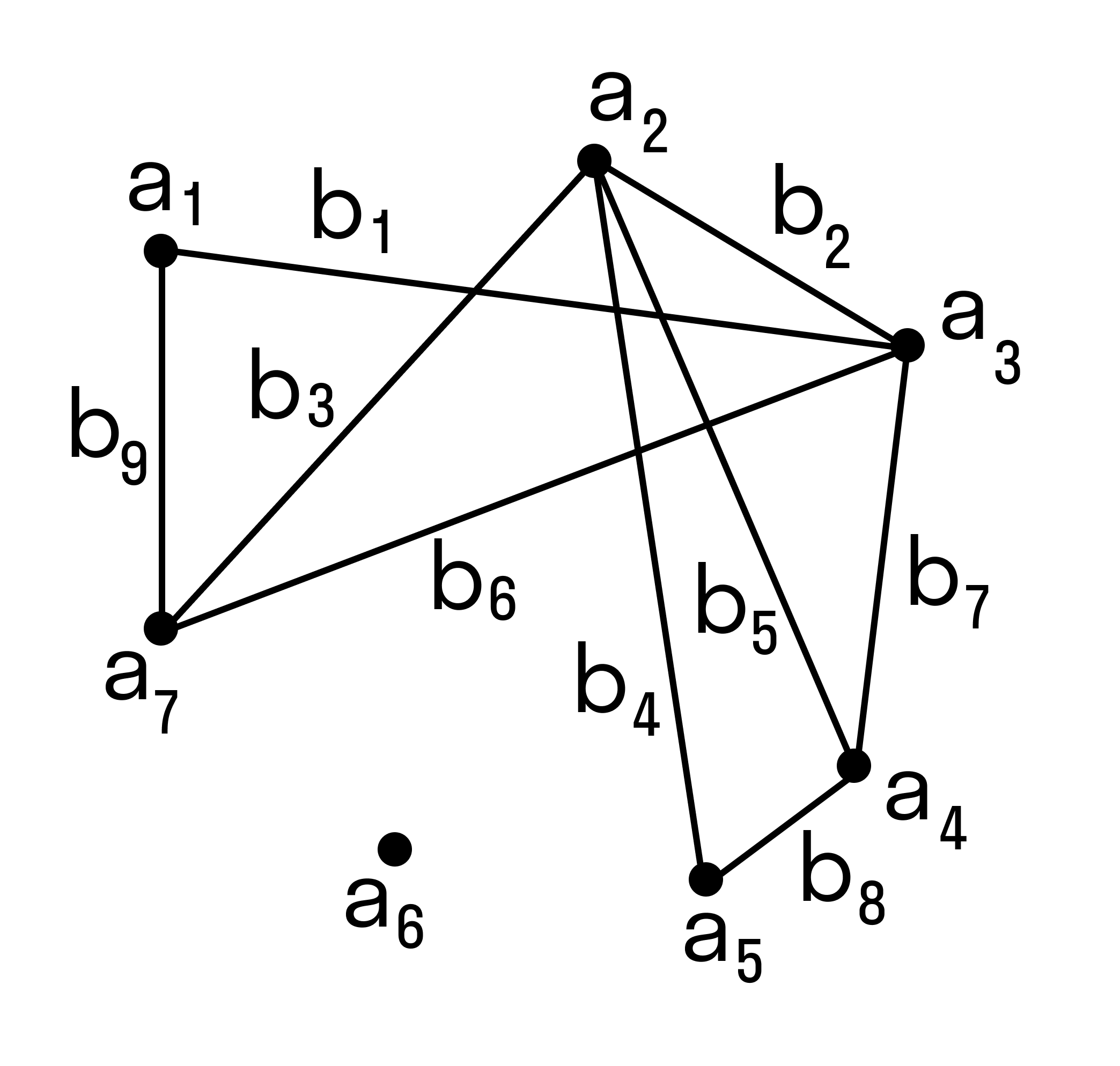
Для н-графа, приведенного на рисунке 7.1, записать 1) маршрут общего вида, 2) не простую цепь, 3) простую цепь, 4) циклический маршрут общего вида,5) не простой цикл, 6) простой цикл.

Решение:

1) Маршрут общего вида – это маршрут, в котором начальная и конечная вершина различны, и некоторые ребра повторяются. М₁ = (1, 4, 5, 1, 4, 7, 3). Здесь повторяется ребро (1, 4).

2) Не простая цепь – это маршрут, в котором не повторяются ребра, но повторяются вершины. М₂ = (4, 3, 1, 5, 6, 7, 4, 1). Здесь повторяется вершина 1.

3) Простая цепь – это маршрут, в котором не повторяются вершины. М₃ = (4, 3, 7, 5, 6).

4) Циклический маршрут общего вида – это маршрут, в котором начальная и конечная вершины совпадают, и некоторые ребра повторяются. М₄ = (1, 5, 1, 5, 1). Здесь повторяется ребро (1, 5).

Рисунок 7.1. Построение маршрутов

в неориентированном графе

5) Непростой цикл – это циклический маршрут, в котором не повторяются ребра, но повторяются вершины. М₅ = (3, 4, 5, 7, 4, 1, 3). Здесь повторяется вершина 4.

Заметим, что непростой цикл бывает только в графах, в которых существует конфигурация типа «песочные часы».

6) Простой цикл – это циклический маршрут, в котором не повторяются вершины. М₆ = (5, 4, 3, 2, 1, 5).

Пример 7.2.

Для н-графа, приведенного на рисунке 7.1, построить матрицу расстояний. Определить диаметр и радиус графа. Указать центры графа. Записать диаметральные и радиальные цепи

Решение:

Для построения матрицы расстояний, сопоставим строки и столбцы вершинам. На пересечении строк и столбцов укажем расстояние между соответствующими вершинами.

d(a, b)	1	2	3	4	5	6	7
1	0	1	1	1	1	2	2	2
2	1	0	1	2	2	3	2	3
3	1	1	0	1	2	2	1	2
4	1	2	1	0	1	2	1	2
5	1	2	2	1	0	1	1	2
6	2	3	2	2	1	0	1	3
7	2	2	1	1	1	1	0	2

На месте (1, 1) стоит 0, так как кратчайший маршрут между вершиной 1 и вершиной 1 – это вырожденный маршрут (без ребер) длины 0.

На месте (1, 2) стоит 1, так как кратчайший маршрут между вершиной 1 и вершиной 2 – это единственное ребро, связывающее эти вершины.

На месте (1, 6) стоит 2, так как кратчайшая простая цепь, между вершиной 1 и вершиной 6 – это цепь из двух ребер (1, 5, 6). Значит, расстояние между этими вершинами равно 2.

В последнем столбце таблицы указано расстояние от данной вершины до наиболее удаленной от нее вершины – эксцентриситет. Их значения находим по формуле (7.1).

Максимум значений последнего столбца – диаметр графа. Откуда d(G) = 3.

Минимум значений последнего столбца – радиус графа. Откуда r(G) = 2.

Центрами являются вершины: 1, 3, 4, 5, 7. Их эксцентриситеты равны радиусу графа.

Для построения диаметральных цепей выясним с помощью матрицы расстояний, какие вершины наиболее удалены друг от друга. Так как максимальное расстояние между вершинами – это диаметр графа, значит, найдем вершины, находящиеся на расстоянии, равном диаметру. Это вершины 2 и 6. Следовательно, все диаметральные цепи в графе связывают эти вершины. Таких цепей две:

Для построения радиальных цепей выясним с помощью матрицы расстояний, какие вершины наиболее удалены от центров.

От центра 1 на расстоянии радиуса, равного 2, находятся вершины 6 и 7. Значит можно провести радиальные цепи:

От центра 3 на расстоянии радиуса находятся вершины 5 и 6. Значит можно провести радиальные цепи:

Дата добавления: 2018-04-15 ; просмотров: 5486 ; Мы поможем в написании вашей работы!

Источник

Теория графов. Основные понятия и виды графов

Теория графов

В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.

Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.

Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.

Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.

Давайте на примере.

На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.

Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:

В данном случае точки — это вершины графа, а связки — рёбра графа.

Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.

Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.

Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.

Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.

Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.

Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.

Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.

Основные понятия теории графов

Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.

Лемма о рукопожатиях

В любом графе сумма степеней всех вершин равна удвоенному числу ребер.

Доказательство леммы о рукопожатиях

Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.

Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).

Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.

Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.

Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.

Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.

Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.

Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.

Путь и цепь в графе

Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Циклом называют путь, в котором первая и последняя вершины совпадают.

Путь или цикл называют простым, если ребра в нем не повторяются.

Если в графе любые две вершины соединены путем, то такой граф называется связным.

Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.

Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.

Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:

Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.

Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.

Визуализация графовых моделей

Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.

Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.

Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.

Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.

Виды изобразительных соглашений:

Виды графов

Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.

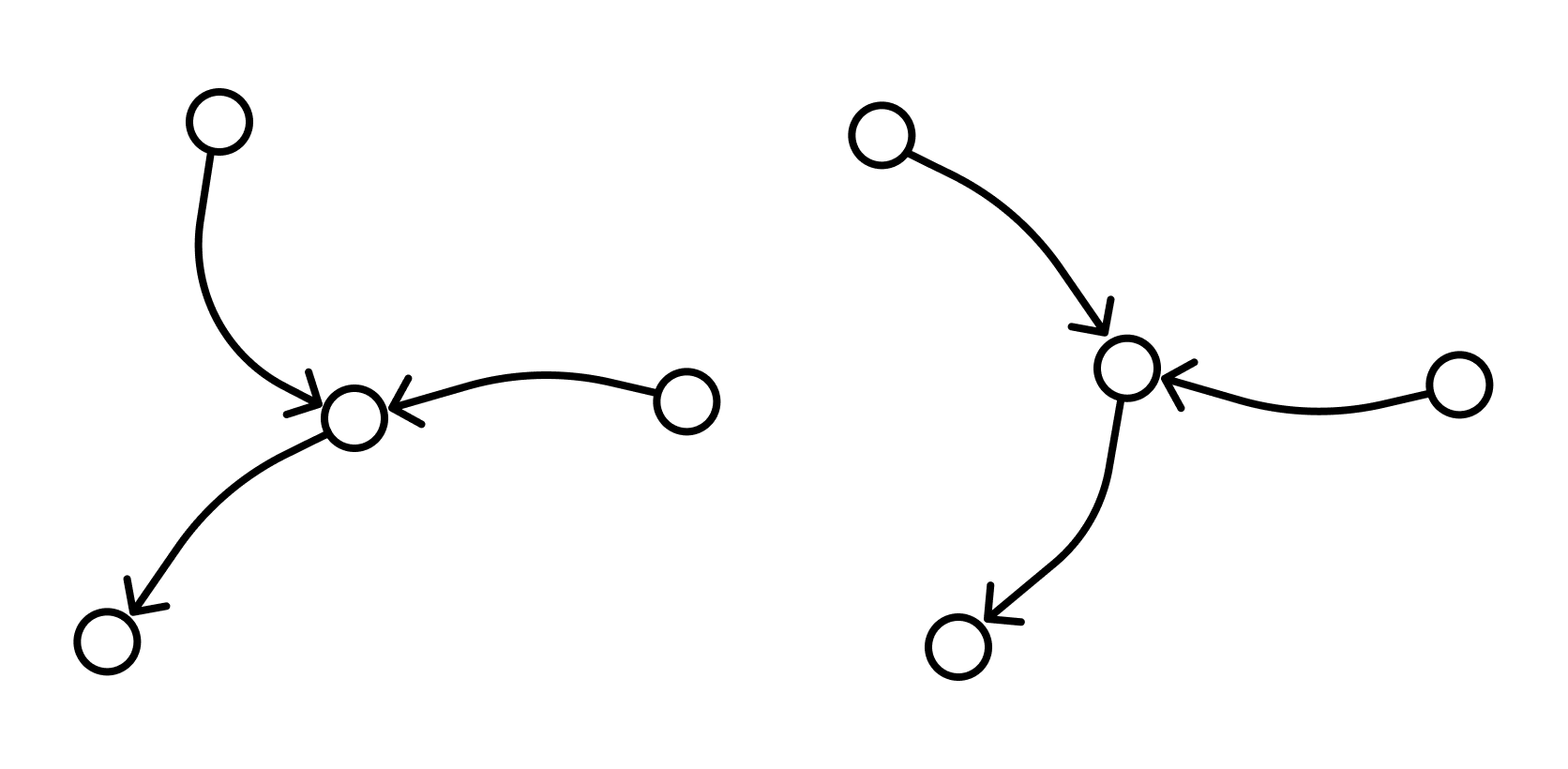
Ориентированные и неориентированные графы

Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.

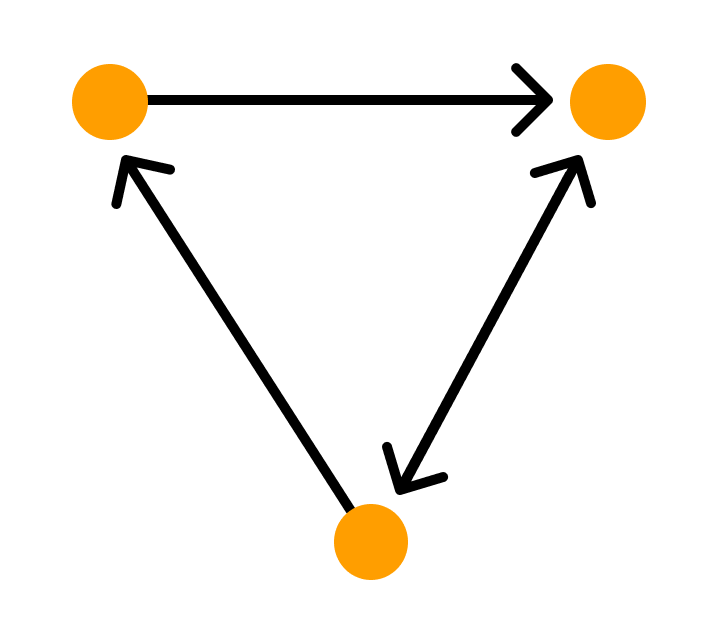
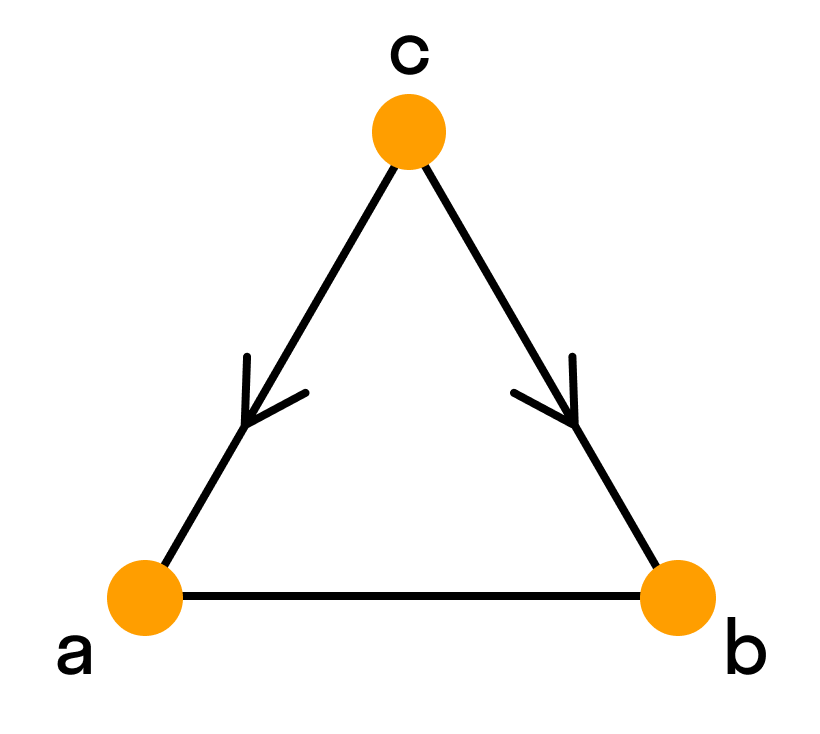
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.

Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.

Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы

Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».

Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).

Пустой граф — это тот, что состоит только из голых вершин.

Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.

Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.

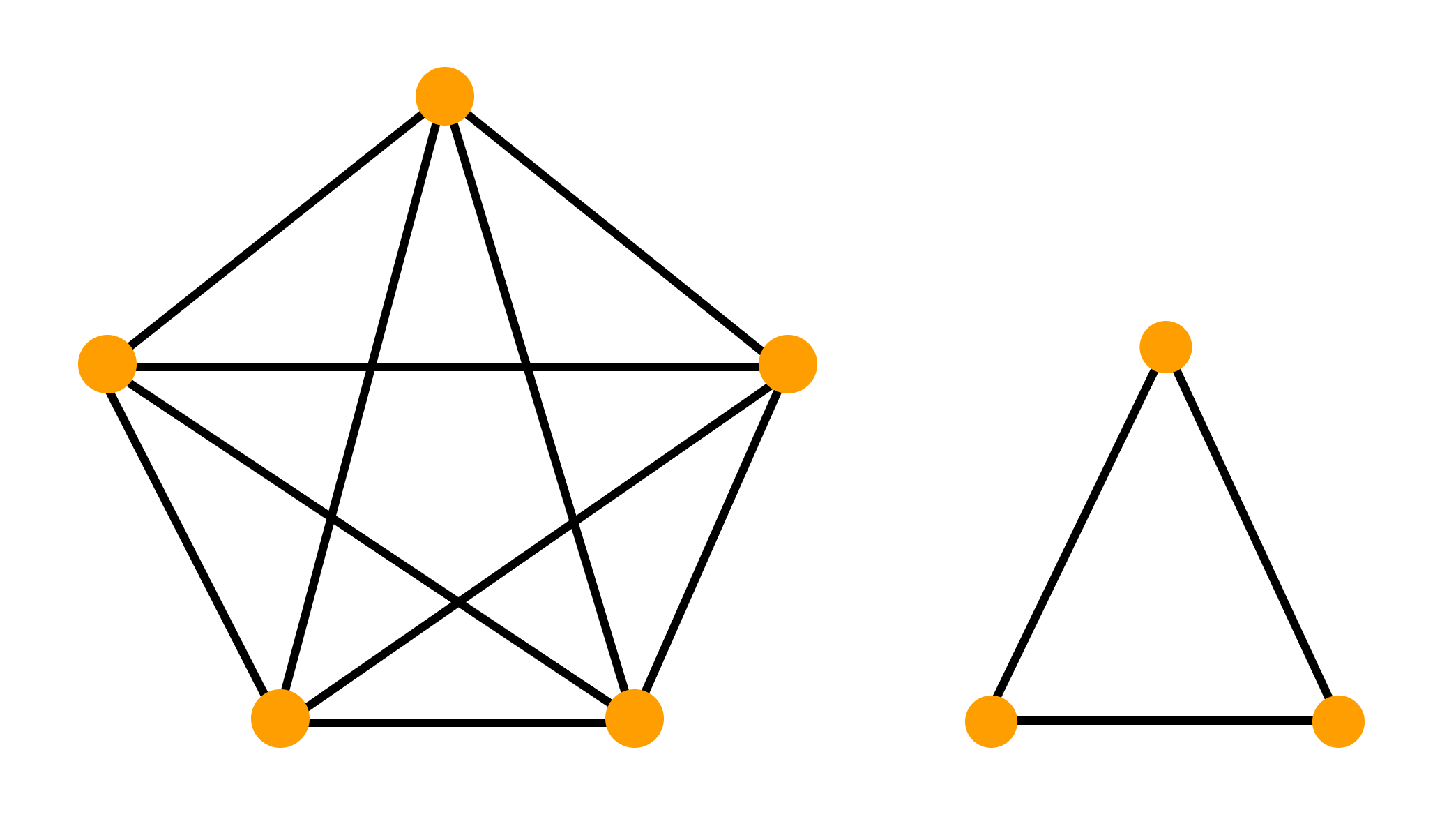
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.

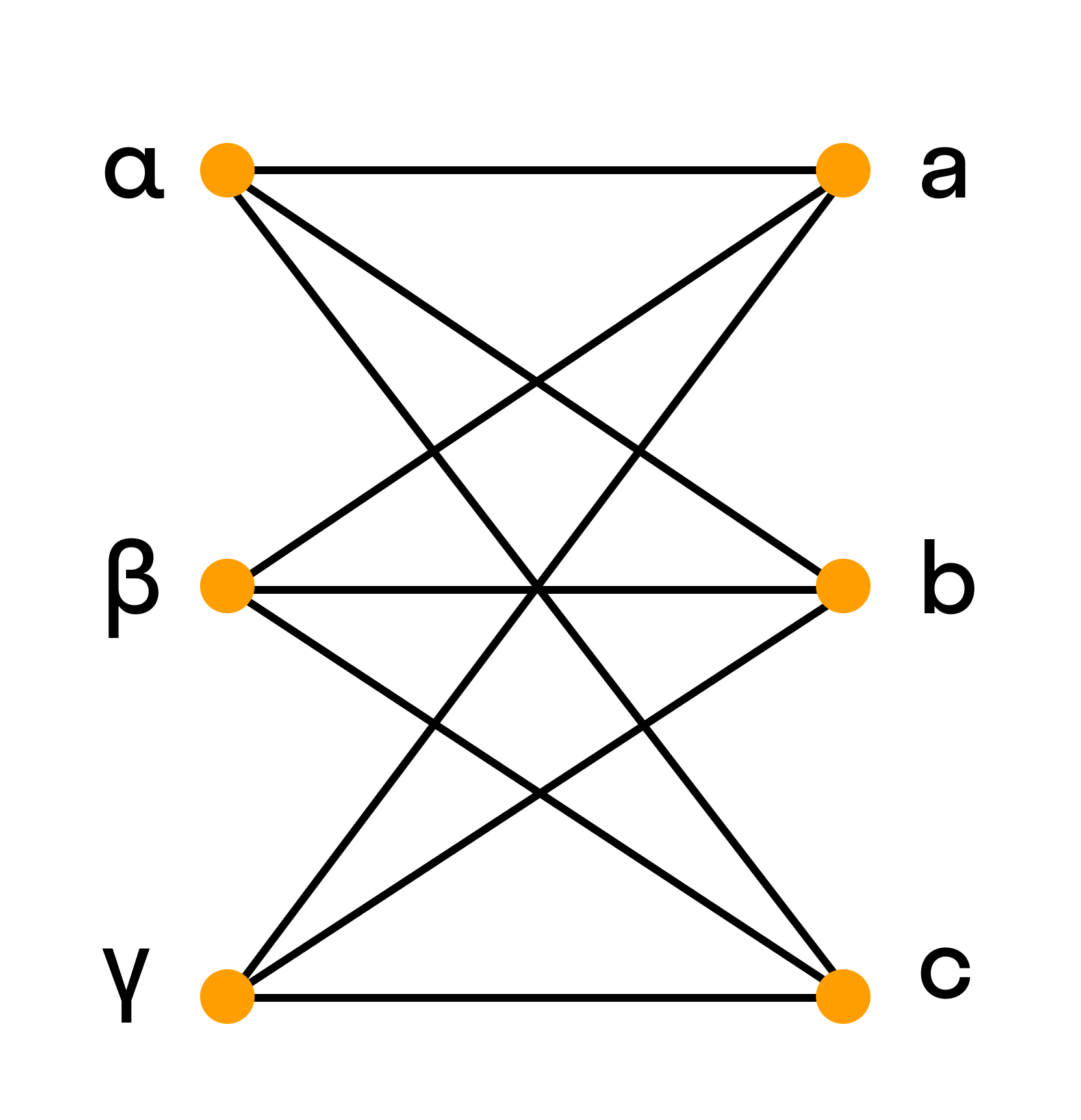
Двудольный граф

Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.

Эйлеров граф

Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.

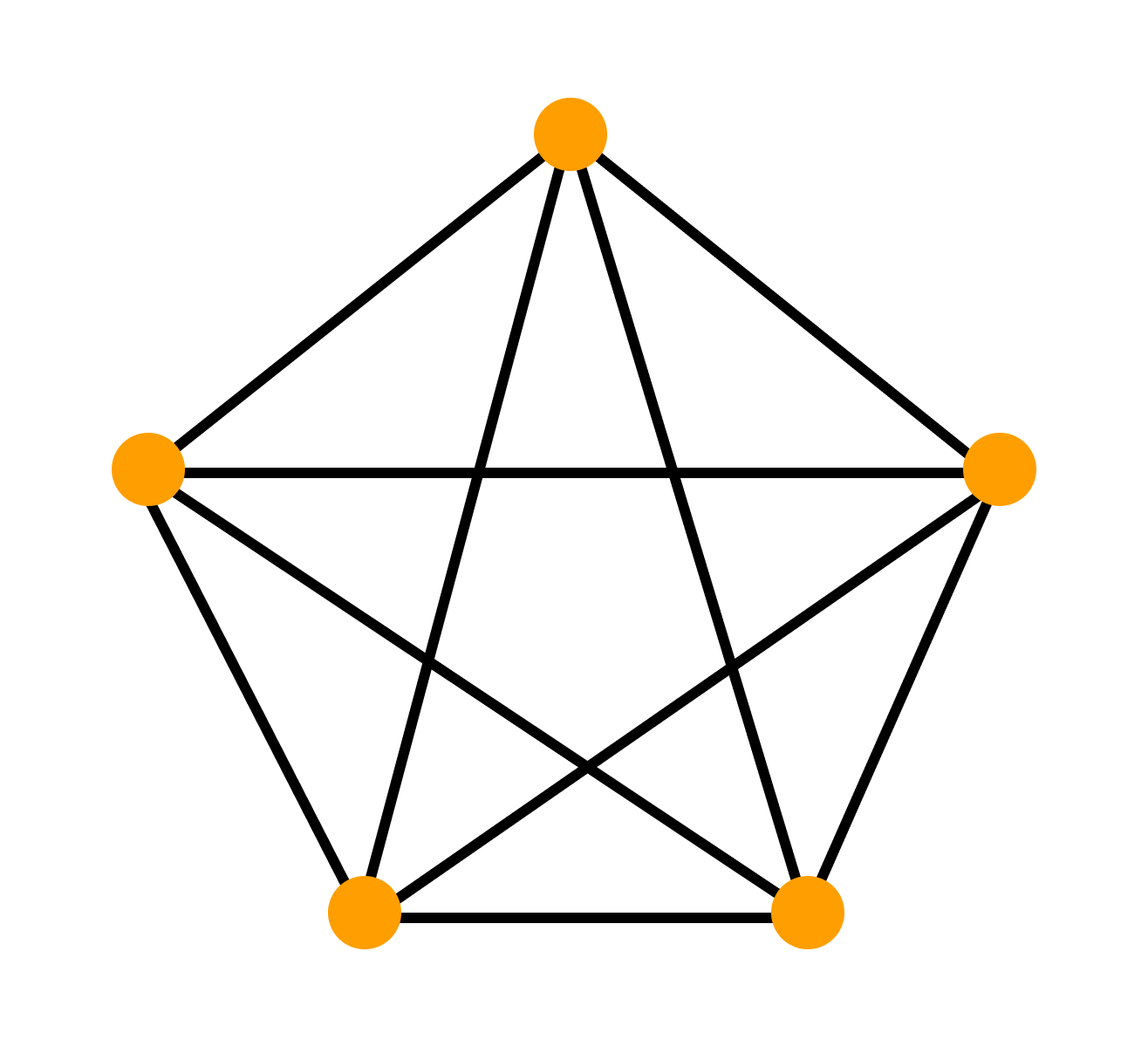
Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?

Регулярный граф

Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.

Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.

Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.

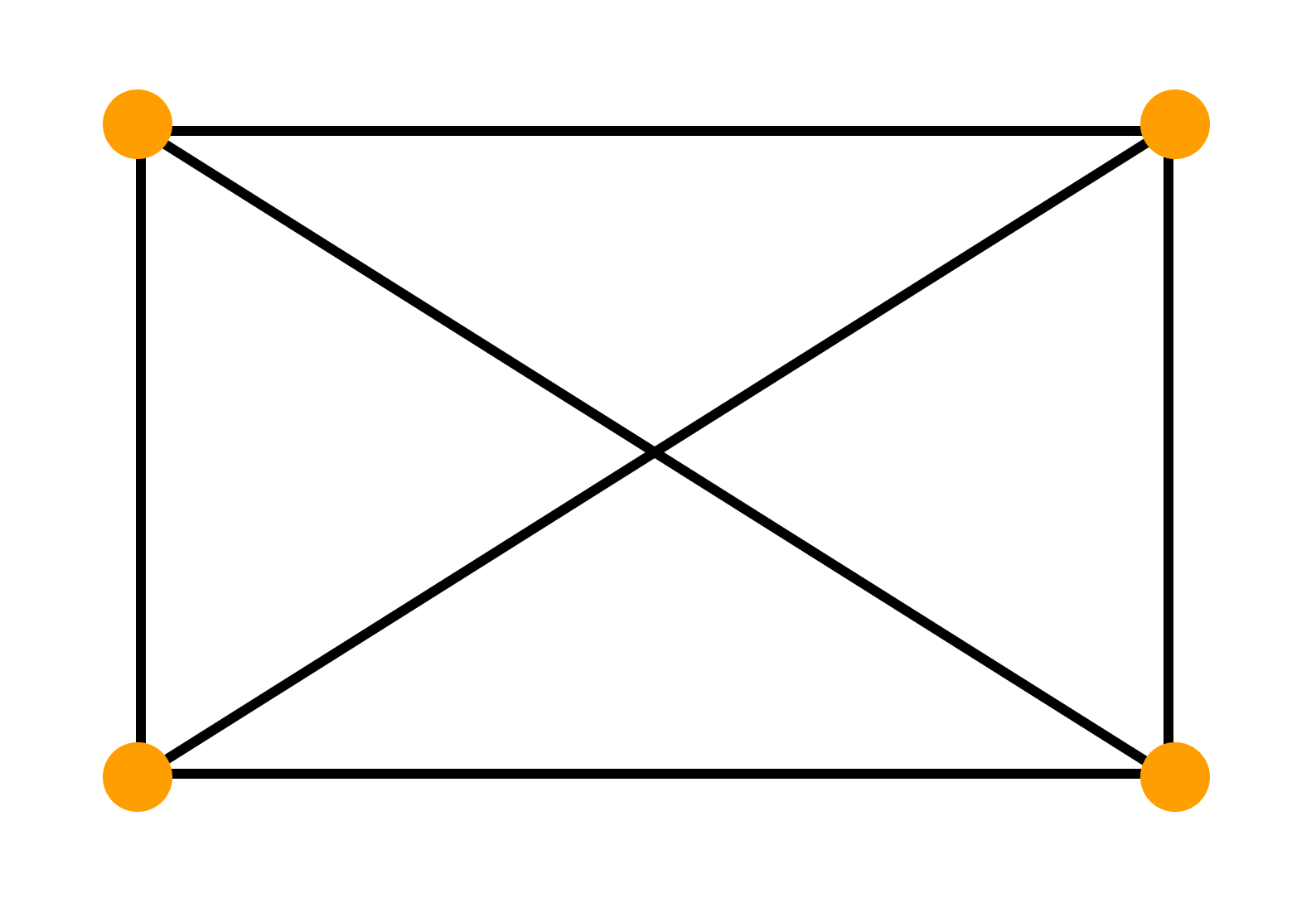
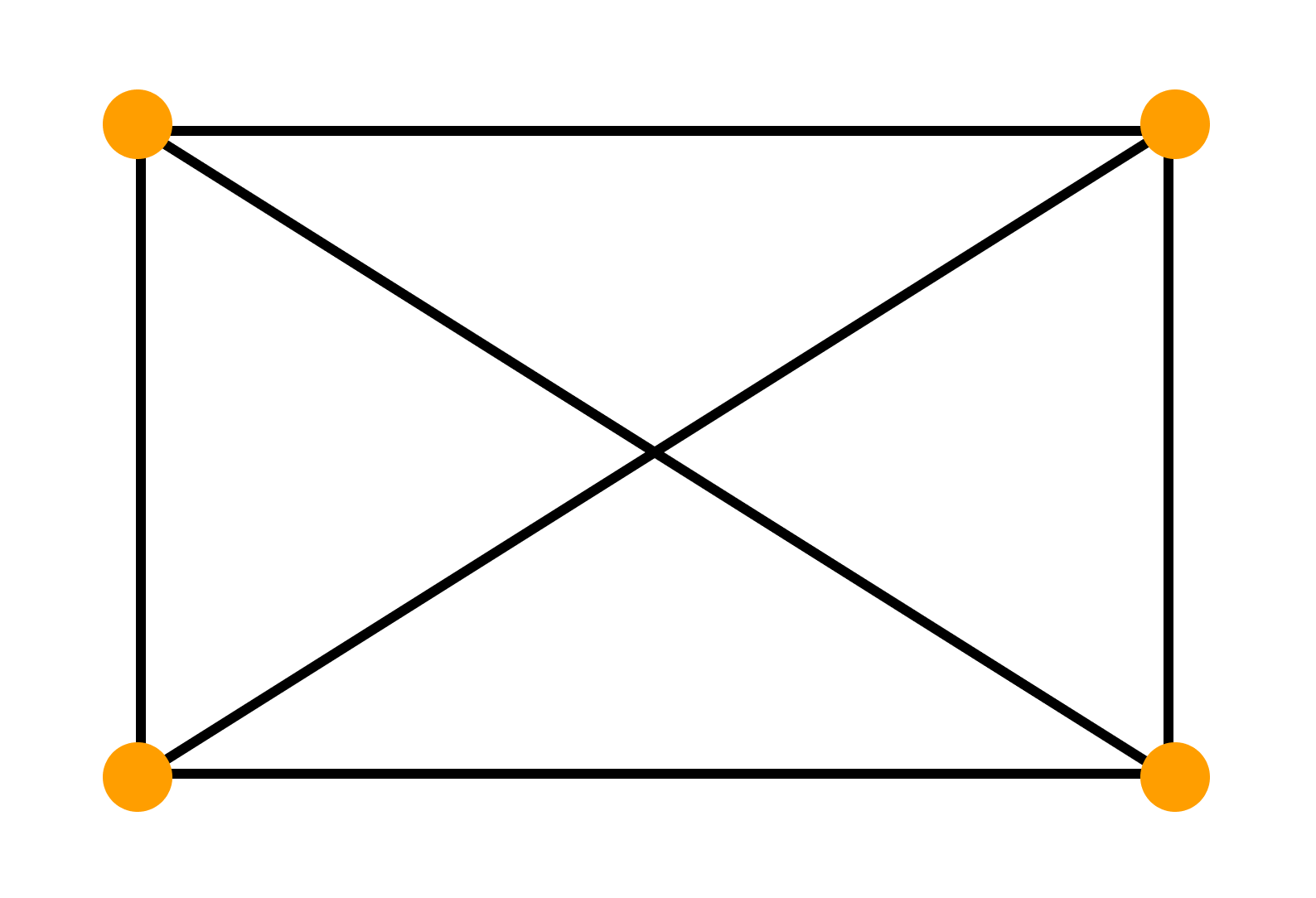
Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.

Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:

Гамильтонов граф

Гамильтоновым графом называется граф, содержащий гамильтонов цикл.

Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.

Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.

Взвешенный граф

Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.

Графы-деревья

Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.

Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.

Определение дерева

Деревом называется связный граф, который не содержит циклов.

Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.

Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.

Простым путем называется путь, в котором никакое ребро не встречается дважды.

Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:

Дерево — минимальный по числу рёбер связный граф.

Висячей вершиной называется вершина, из которой выходит ровно одно ребро.

Определения дерева:

Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.

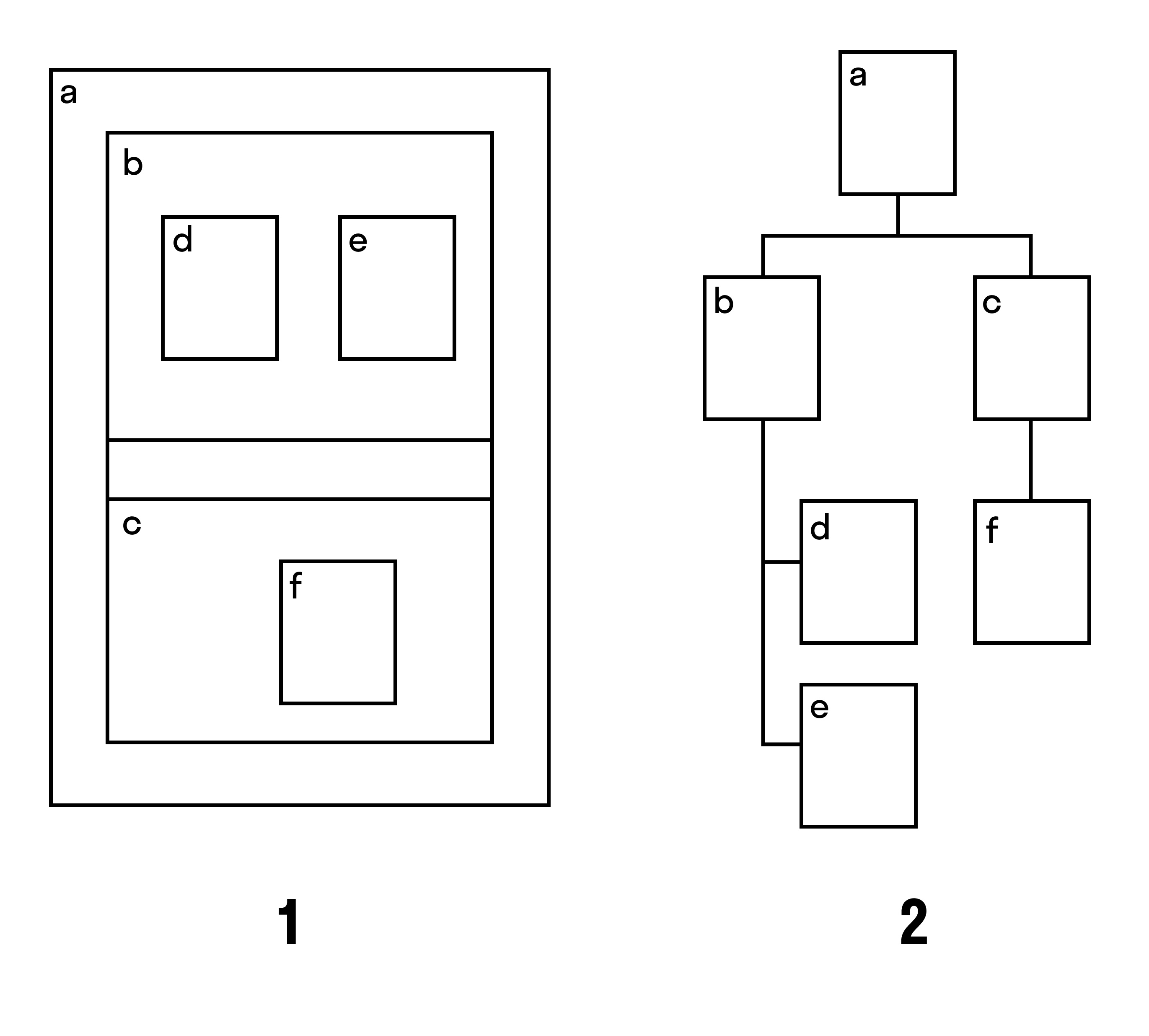
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.

Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:

Теоремы дерева и их доказательства

В дереве с более чем одной вершиной есть висячая вершина.

Доказательство первой теоремы:

Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.

Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.

В дереве число вершин на 1 больше числа ребер.

Доказательство второй теоремы:

Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n

У любого связного графа есть остовное дерево.

Доказательство третьей теоремы:

Чтобы найти остовное дерево графа G, можно найти цикл в графе G и выкинуть одно ребро цикла — потом повторить. И так пока в графе не останется циклов. Полученный граф будет связным, так как мы выкидывали рёбра, не нарушая связность, но в нём не будет циклов. Значит, он будет деревом.

Теория графов и современные прикладные задачи

На основе теории графов создали разные методы решения прикладных задач, в которых в виде графов можно моделировать сложные системы. В этих моделях узлы содержат отдельные компоненты, а ребра отражают связи между компонентами.

Графы и задача о потоках

Система водопроводных труб в виде графа выглядит так:

Каждая дуга графа отображает трубу. Числа над дугами (весы) — пропускная способность труб. Узлы — места соединения труб. Вода течёт по трубам только в одном направлении. Узел S — источник воды, узел T — сток.

Задача: максимизировать объём воды, протекающей от источника к стоку.

Для решения задачи о потоках можно использовать метод Форда-Фулкерсона. Идея метода в том, чтобы найти максимальный поток по шагам.

Сначала предполагают, что поток равен нулю. На каждом последующем шаге значение потока увеличивается, для чего ищут дополняющий путь, по которому поступает дополнительный поток. Эти шаги повторяют до тех пор, пока существуют дополнительные пути.

Задачу успешно применяют в различных распределенных системах: система электроснабжения, коммуникационная сеть, система железных дорог.

Графы и сетевое планирование

В задачах планирования сложных процессов, где много разных параллельных и последовательных работ, часто используют взвешенные графы. Их еще называют сетью ПЕРТ (PERT).

PERT (Program (Project) Evaluation and Review Technique) — техника оценки и анализа программ (проектов), которую используют при управлении проектами.

Сеть ПЕРТ — взвешенный ациклический ориентированный граф, в котором каждая дуга представляет работу (действие, операцию), а вес дуги — время, которое нужно на ее выполнение.

Если в сети есть дуги (a, b) и (b, c), то работа, представленная дугой (a, b), должна быть завершена до начала выполнения работы, представленной дугой (b, c). Каждая вершина (vi) представляет момент времени, к которому должны быть завершены все работы, задаваемые дугами, оканчивающимися в вершине (vi).

Путь максимальной длины между этими вершинами графа называется критическим путем. Чтобы выполнить всю работу быстрее, нужно найти задачи на критическом пути и придумать, как их выполнить быстрее. Например, нанять больше людей, перепридумать процесс или ввести новые технологии.

Источник

• ← что такое паралич головного мозга
• что такое нотариальное тождество →