что такое действительное изображение

Оптика. Линза. Собирающая линза. Действительное и мнимое изображение.

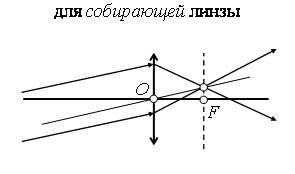
Собирающая линза – это линза которая в средней части толще, чем по краям. Если на собирающую линзу попадает пучок лучей, параллельных главной оптической оси, то после преломления в линзе они собираются в одной точке F, которую обозначают как главный фокус линзы.

Посредствам линз получится делать увеличенные и уменьшенные изображения объектов.

Опыты демонстрируют: отчётливое изображение формируется, когда объект, линза и экран размещены на определённых расстояниях друг от друга. В зависимости от их взаимного положения изображения могут быть перевёрнутыми или прямыми, увеличенными или уменьшенными, действительными или мнимыми.

Изображение, даваемое собирающей линзой, в зависимости от соотношения дистанции d от предмета до линзы и ее фокусным расстоянием F:

— d 2F – уменьшенное, перевернутое, действительное (предмет расположен за точкой двойного фокуса, пример – фотоаппарат, глаз).

Когда изображение действительное, его получится спроецировать на экран. В этом случае изображение будет видно из всякой точки комнаты, из которой виден экран.

Когда изображение мнимое, то его не получится спроецировать на экран, а можно только увидеть глазом, располагая его определённым образом по отношению к линзе (нужно смотреть «в неё»).

Источник

Учебники

Журнал «Квант»

Общие

Содержание

Действительное и мнимое изображения

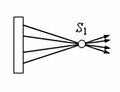
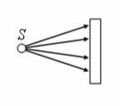
Пусть падающие на оптическую систему лучи после преломления выходят сходящимся пучком лучей, пересекающихся в точке S₁ (рис. 1 а, оптическая система изображена прямоугольником). В этом случае S₁ – это действительное изображение.

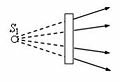
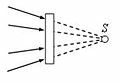
Если из оптической системы вышел расходящийся пучок лучей и продолжения этих лучей пересекаются в точке S₁ (рис. 1 б), то S₁ – это мнимое изображение.

Линза

При решении задач с системой линз задача разбивается на несколько частей (по числу линз):

1 часть – рассматривается только первая к предмету линза (все остальные линзы не рассматриваются и никак не влияют на решение); 2 часть – рассматривается только вторая линза, а предметом для нее служит изображение от первой линзы и т.д.

Построение в линзах

При построении изображения точек выбирают любые два из трех стандартных лучей.

Виды изображения

1) действительное или мнимое;

2) прямое или перевернутое;

3) увеличенное или уменьшенное.

Дополнительные лучи при построении

При построении можно воспользоваться следующим свойством:

все лучи света, направленные параллельно побочной оптической оси, после преломления собираются в побочном фокусе (рис. 4).

Оптическая сила линзы

где F – фокус линзы (м); D – оптическая сила линзы (дптр). ОБРАТИТЕ ВНИМАНИЕ, что в некоторой физической литературе учитывают знаки в величинах, тогда:

где D₀ – оптическая сила системы вплотную сложенных N тонких линз (дптр); D₁, D₂, …, D_N – оптические силы тонких линз системы (дптр).

Формула тонкой линзы

Пусть на оптическую систему падает расходящийся пучок лучей, пересекающихся в точке S (рис. 5 а, оптическая система изображена прямоугольником). В этом случае S – это действительный источник (предмет).

Если на оптическую систему падает сходящийся пучок лучей и продолжения этих лучей пересекаются в точке S (рис. 5 б), то S – это мнимый источник (предмет).

Увеличение линзы

где Г – увеличение линзы; H – высота изображения (м); h – высота предмета (м).

где Г – увеличение линзы; f – расстояние от изображения до линзы (м); d – расстояние от предмета до линзы (м).

Оптические приборы

где Г_l – увеличение лупы; d₀ – расстояние наилучшего зрения (для нормального глаза), равное 0,25 м; F – фокусное расстояние лупы (м).

Для нормального (здорового) глаза расстояние наилучшего зрения равно d₀ = 25 см.

Ближний предел аккомодации – это наименьшее расстояние, на которое можно рассматривать предметы, максимально напрягая мышцы глаз.

Источник

Разница между действительным и мнимым изображением

Наше зрение распознает предметы благодаря тому, что они испускают свет (часто он является отраженным). Но лучи от объекта могут встретить на своем пути препятствие в виде какой-либо оптической системы. В результате изображение получается действительным или мнимым. Что подразумевается под этими названиями, как в каждом случае происходит перемещение лучей, и чем отличается действительное изображение от мнимого? Об этом рассказывается ниже.

Общие сведения

Лучи от обычного предмета поступают в окружающее пространство в виде расходящегося пучка. Если взять некоторый точечный источник и пропустить свет от него через преломляющую или отражающую систему, то сформируется изображение, называемое оптическим. Оно будет представлять собой точку, в которой сойдутся лучи или их продолжения (воображаемые линии с обратным направлением) после прохождения через такую систему.

Сравнение

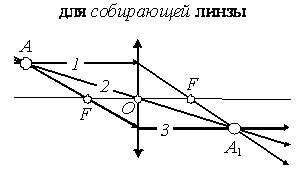
Чтобы разобраться, в чем состоит отличие действительного изображения от мнимого, рассмотрим два рисунка. Вот первый из них:

Здесь точечный источник обозначен буквой A. Он распространяет расходящиеся лучи. На определенном расстоянии расположена некоторая оптическая система (L). Лучи проходят через эту преломляющую среду, меняют свое направление и устремляются к точке A1. Именно она и является действительным, то есть образованным самими лучами, изображением источника A.

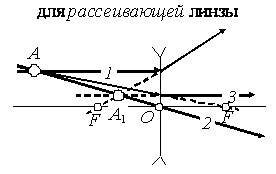
Теперь второй случай:

Снова имеем источник света A. Лучи от него движутся к системе L и тоже меняют направление. Только теперь они расходятся. А изображение при этом формируется в месте, где могли бы пересекаться лучи, перемещаясь в обратную сторону (их так называемое продолжение отмечено пунктиром). Точка A1 – мнимое, не созданное непосредственно лучами, изображение.

Какие оптические приборы или предметы позволяют наблюдать каждый из вариантов? В случае с действительным изображением это, скажем, собирающая линза. А с мнимым – лупа, обычное ровное зеркало.

В чем разница между действительным и мнимым изображением еще? В том, что первое из них нельзя увидеть просто «в воздухе». Здесь требуется проекция на поверхность, размещенную в плоскости пересечения прошедших через оптическую среду лучей, например на экран или фотоматрицу. Мнимое изображение зарегистрировать таким образом нельзя. Но его можно просто увидеть или сфотографировать.

Источник

Действительное изображение

На практике часто меняют масштаб изображения предметов и проецируют его на какую-либо поверхность.

Содержание

Свойства

Соответствие объекту достигается, когда каждая его точка изображается точкой, хотя бы приблизительно. При этом различают два случая: действительное изображение и мнимое изображение.

Во всякой реальной оптической системе неизбежно присутствуют аберрации, в результате чего лучи (или их продолжения) не сходятся идеально в одной точке, и кроме того, максимально близко сходятся не совсем там, где нужно. Изображение получается несколько размытым и геометрически не полностью подобным предмету; возможны и другие дефекты.

Пучок лучей, который расходится из одной точки или сходится в ней, называется гомоцентрическим. Ему соответствует сферическая световая волна. Задача большинства оптических систем — преобразовывать расходящиеся гомоцентрические пучки в гомоцентрические же, тем самым создавая мнимое или действительное изображение, чаще всего, в другом масштабе по отношению к предмету.

Стигматическое изображение (от др.-греч. στίγμα — укол, рубец) — оптическое изображение, каждая точка которого соответствует одной точке изображаемого оптической системой объекта.

Стигматическое изображение не обязательно геометрически подобно изображаемому объекту, но если оно подобно, такое изображение называется идеальным. Это возможно лишь при условии, что в оптической системе отсутствуют или устранены все аберрации, и что возможно пренебречь волновыми свойствами света. Оптическую систему, которая создаёт идеальное изображение, называют идеальной оптической системой. Идеальными можно приближённо считать центрированные системы, в которых изображение получается с помощью монохроматических и параксиальных пучков света.

Хотя глазом человека действительные и мнимые изображения воспринимаются одинаково, при формировании действительного изображения пересечение лучей реальное, и эти реальные лучи могут подействовать, например, на фотоплёнку, вызвав в ней химические преобразования, или быть зафиксированы фотоэлементом.

Мнимое изображение натурального размера, создаваемое зеркалом

Источник

Построение изображения в линзе

теория по физике 🧲 оптика

Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.

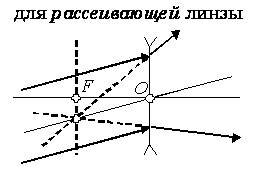
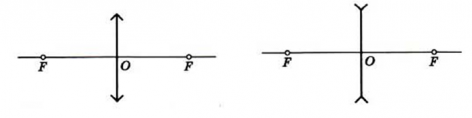
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.

Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.

Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.

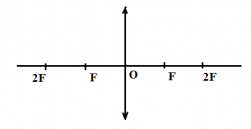
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.

Построение изображения в собирающей линзе

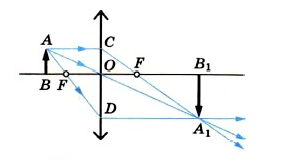
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:

Два вида лучей при построении изображений в линзе

Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).

Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.

На пересечении двух лучей обозначаем точку А₁. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В₁. Изображение предмета при этом — А₁ В_1.

В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.

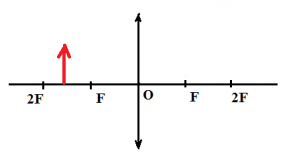
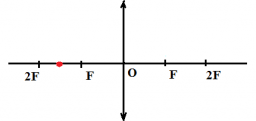
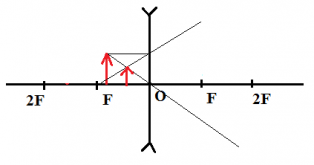
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.

Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.

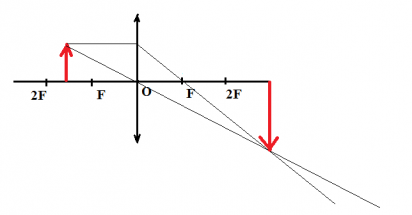
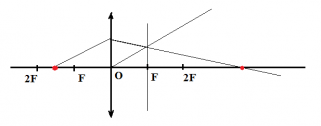
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.

Частный случай — построение изображения точки

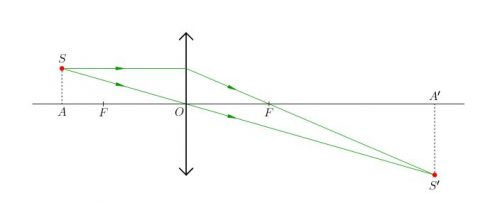
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.

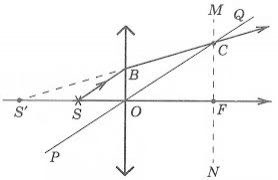
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.

Пример №2. Построить изображение точки, расположенной на главной оптической оси.

Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.

Построение изображения в рассеивающей линзе

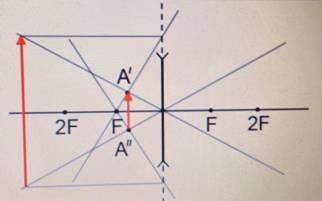
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).

Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.

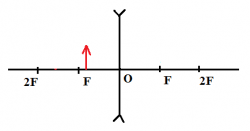
Пример №3. Построить изображение предмета в рассеивающей линзе.

Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.

Построение изображений в плоском зеркале

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.

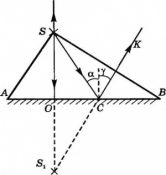
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S₁, которое представляет собой точку пересечения продолжения отраженных лучей.

Таким образом, чтобы получить изображение в плоском зеркале, нужно:

Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.

Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S₁OC равны по стороне и двум углам. Следовательно SO = S₁O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.

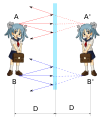
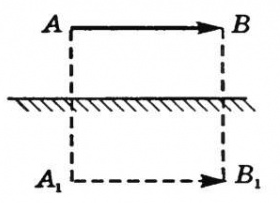
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А₁В₁ соответствует предмету АВ.

Изображение и сам предмет всегда симметричны относительно зеркала.

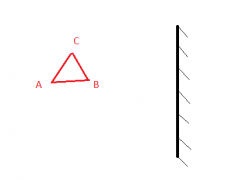
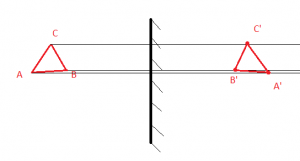
Пример №4. Построить изображение треугольника ABC в плоском зеркале.

Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.

Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник