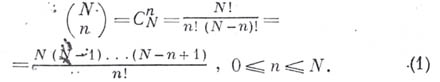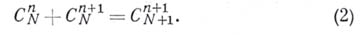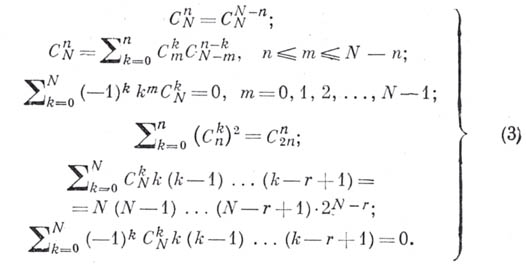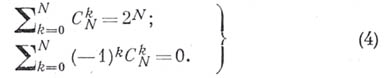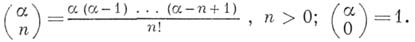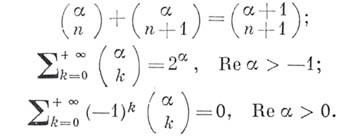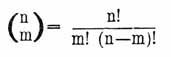что такое биномиальный коэффициент
Расчет биномиальных коэффициентов на Си (С++) и Python
При решении задач комбинаторики часто возникает необходимость в расчете биномиальные коэффициентов. Бином Ньютона, т.е. разложение 


Прежде чем перейти к написанию процедур расчета, рассмотрим так называемый треугольник Паскаля.
или он же, но немного в другом виде. В левой колонке строки значение n, дальше в строке значения 
В полном соответствии с рекуррентной формулой значения 

Ниже для биномиальных коэффициентов 
Расчет биномиальных коэффициентов через факториальную формулу
поскольку биномиальные коэффициенты неотрицательные, будем использовать в расчетах беззнаковый тип.
Значение в очередной строке должно быть примерно в 2 раза больше, чем в предыдущей. Поэтому последний правильно вычисленный коэффициент (см треугольник выше) — это C(12,6) Хотя unsigned int вмещает 4млрд, правильно вычисляются значения меньше 1000. Вот те раз, почему так? Все дело в нашей процедуре bci, точнее в строке, которая сначала вычисляет большое число в числителе, а потом делит его на большое число в знаменателе. Для вычисления C(13,6) сначала вычисляется 13!, а это число > 6млрд и оно не влезает в unsigned int.
Как оптимизировать расчет 

Явно лучше, ошибка возникла при расчете C(31,15). Причина понятна — все то же переполнение. Сначала умножаем на 31 (оп-па — переполнение, потом делим на 15). А что, если использовать рекурсивную формулу? Там только сложение, переполнения быть не должно.
Что ж, пробуем:
Все, что влезло в unsigned int, посчиталось правильно. Вот только строчка с n=34 считалась около минуты. При расчете C(n,n/2) делается два рекурсивных вызова, поэтому время расчета экспоненциально зависит от n. Что же делать — получается либо неточно, либо медленно. Выход — в использовании 64 битных переменных.
Замечание по результатам обсуждений: в конце статьи добавлен раздел, где приведен простой и быстрый вариант «bcr с запоминанием» одного из участников обсуждения.
Использование 64 битных типов для расчета C(n,k)
2.8*10 19 уже не влезает в unsigned long long
Дальнейшее повышение точности и расчет при n>67
Для экстремалов и «олимпийцев»
В принципе, для практических задач точности функции bcd достаточно, но в олимпиадных задачах часто даются тесты «на грани». Т.е. теоретически может встретится задача, где точности double недостаточно и C(n,k) влезает в unsigned long long еле-еле. Как избежать переполнения для таких крайних случаев? Можно использовать рекурсивный алгоритм. Но если он для n=34 считал минуту, то для n=67 будет считать лет 100. Можно запоминать рассчтанные значения (см Дополнение после публиукации).Также можно использовать рекурсию не для всех n и k, а только для «достаточно больших». Вот процедура расчета, которая считает правильно для n 67 при малых k (к примеру, считает C(82,21)=1.83*10 19 ).
В какой-то из олимпиадных задач мне потребовалось вычислять много C(n,k) для n >70, т.е. они заведомо не влезали в unsigned long long. Естественно, пришлось использовать «длинную арифметику» (свою). Для этой задачи я написал «рекурсию с памятью»: вычисленные коэффициенты запоминались в массиве и экспоненциального роста времени расчета не было.
Дополнение после публикации
При обсуждении часто упоминаются варианты с запоминанием рассчитанных значений. У меня есть код с динамическим выделением памяти, но я его не привел. На даный момент вот самый простой и эффективный из комментария chersanya: http://habrahabr.ru/post/274689/#comment_8730359http://habrahabr.ru/post/274689/#comment_8730359
Если в программе надо использовать [почти] все коэффициенты треугольника Паскаля (до какого-то уровня), то приведенный рекурсивный алгоритм с запоминанием — самый быстрый способ. Аналогичный код годится и для unsigned long long и даже для длинной арифметики (хотя там, наверное, лучше динамически вычислять и выделять требуемый объем памяти). Конкретные значения N_MAX могут быть такими:
35 — посчитает все коэффициенты C(n,k), n 19
K_MAX — это может быть N_MAX/2+1, но не больше 35, поскольку C(68,34) за границей unsigned long long.
Для простоты можно всегда брать K_MAX=35 и не думать «войдет — не войдет» (до тех пор, пока не перейдем к числами с разрядностью >64 бита).
Расчет биномиальных коэффициентов на Python
Это дополнение появилось спустя примерно погода после публикации статьи. Автор начал осваивать Python и для тренироки я решаю олимпиадные задачи, сделанные ранее на C++. Для задач связанных в точными/длинными вычислениями приходится либо всячески исхитряться (как при расчетах биномиальных коэфиициентов), дабы избежать раннего переполнения, либо смиряться с потерей точности (перейдя к типу double) либо писать(или искать) длинную арифметику. В Python длинная арифметика уже есть, поэтому тут для вычисления биномиальных коэффициентов достаточно реализовать запоминание. Запоминать их будем в списке (передается в функцию как папаметр).
Вот вывод (без таблички)
270288240945436569515614693625975275496152008446548287007392875106625428705522193898612483924502370165362606085021546104802209750050679917549894219699518475423665484263751733356162464079737887344364574161119497604571044985756287880514600994219426752366915856603136862602484428109296905863799821216320
0.4200884663301988
Меньше полсекуды для такого коэффициента
C(68,34) (напомню — он не влезает в long long) считается за 0.017 сек и равен 28453041475240576740
Расчет биномиальных коэффициентов с использованием Фурье-преобразований
При решении задач комбинаторики часто возникает необходимость в расчете биномиальных коэффициентов. Бином Ньютона, т.е. разложение 


Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов не очень сложной задачей для программирования.
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Дискретное преобразование Фурье
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Формулы дискретных преобразований
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
Свёртка двух функций
Фурье-преобразования для вычисления свёртки
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
Биномиальные коэффициенты
Рассмотрим полином F(x)=1+x и его свёртку с самим собой n раз
Fx..xF = SUM С( i, n-1 )*x^i = BFT ( FFT(F)*. *FFT(F) ) = BFT ( FFT(F)^(n-1) )
То есть биномиальные коэффициенты С( i, n-1 ) могут быть получены из значений коэффициентов полинома (1+x)^(n-1)
Программируем:
Проверяем:
Зачем?
При вычислении с помощью треугольника Паскаля трудоёмкость имеет оценку O(n^2).
При вычислении с помощью быстрых Фурье-преобразований трудоёмкость имеет оценку O(n*log n).
БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ
коэффициенты при степенях z в разложений Ньютона бинома 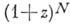
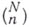
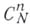
Обозначение 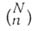
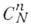
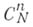
Как понятие Б. к., так и арифметич. треугольник в более или менее развитой форме были известны еще математикам древности, Б. Паскаль (В. Pascal) составил подробное исследование (1665) свойств Б. к. Кроме соотношения (2), имеется много других полезных соотношений между Б. к., напр.:
В частности, отсюда получается
Использование Стирлинга формулы позволяет получать приближенные выражения для Б. к. Напр., если Nмного больше п:
На случай любого комплексного числа 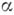
Таблицы Б. к. см. [2], [3].
Лит.:[1] Кори Г., Корн Т., Справочник по математике, пер. с англ., 2 изд., М., 1973; [2] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968; [3] Table of binomial coefficients, Cambridge, 1954. Е. Д. Соломенцев.
Полезное
Смотреть что такое «БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ» в других словарях:
Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых чисел n и k. Явные формулы … Википедия
Биномиальные коэффициенты — коэффициенты в формуле разложения Ньютона бинома … Большая советская энциклопедия
Паскаля треугольник — Биномиальные коэффициенты коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых… … Википедия
Биномиальный коэффициент — В математике биномиальные коэффициенты это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В … Википедия
Ньютона бином — название формулы, выражающей любую целую положительную степень суммы двух слагаемых (бинома, двучлена) через степени этих слагаемых, а именно: (1) (1) где n целое положительное число, а и b какие угодно числа.… … Большая советская энциклопедия
биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… … Энциклопедический словарь
Последовательность Падована — Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия
Бином Ньютона.
Навигация по странице.
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.
Треугольник Паскаля.
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n :
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
Свойства биномиальных коэффициентов.
Первые два свойства являются свойствами числа сочетаний.
Доказательство формулы бинома Ньютона.
Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства 
Получили верное равенство.
Докажем, что верно равенство 
Поехали!
Раскрываем скобки
Группируем слагаемые
Так как 






Подставив эти результаты в полученное выше равенство

придем к формуле бинома Ньютона 
Этим доказана формула бинома Ньютона.
Рассмотрим подробные решения примеров, в которых применяется формула бинома Ньютона.
Напишите разложение выражения (a+b) 5 по формуле бинома Ньютона.
Найдите коэффициент бинома Ньютона для шестого члена разложения выражения 
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Доказать, что значение выражения 
Представим первое слагаемое выражение как 
Биномиальные коэффициенты
Смотреть что такое «Биномиальные коэффициенты» в других словарях:
Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых чисел n и k. Явные формулы … Википедия
Биномиальные коэффициенты — коэффициенты в формуле разложения Ньютона бинома … Большая советская энциклопедия
Паскаля треугольник — Биномиальные коэффициенты коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых… … Википедия
Биномиальный коэффициент — В математике биномиальные коэффициенты это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В … Википедия
Ньютона бином — название формулы, выражающей любую целую положительную степень суммы двух слагаемых (бинома, двучлена) через степени этих слагаемых, а именно: (1) (1) где n целое положительное число, а и b какие угодно числа.… … Большая советская энциклопедия
биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… … Энциклопедический словарь
Последовательность Падована — Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия