что такое бином ньютона простое объяснение

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №31. Сочетания без повторений. Бином Ньютона

Перечень вопросов, рассматриваемых в теме

1) понятие сочетания без повторения и их свойства;

2) правила подсчета числа сочетаний из n-элементов по m без повторений;

4) треугольник Паскаля.

Сочетаниями из n элементов по m в каждом (m ≤ n) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.

Число всевозможных сочетаний из n различных элементов по m элементов обозначают

Формула для подсчёта числа сочетаний:

Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.

Числа являются коэффициентами в формуле бинома Ньютона:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Общим термином «соединения» в комбинаторике называют три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству. Ранее уже рассматривались два вида комбинаций. Это перестановки и размещения. В данных соединениях важен порядок размещения элементов. В случае, когда этот порядок не важен, то мы имеем дело с сочетаниями.

Сочетаниями из n элементов по m в каждом (m ≤ n ) называются такие соединения, каждое из которых содержит m элементов, взятых из данных n различных элементов, и которые отличаются одно от другого по крайней мере одним элементом.

Иногда такие сочетания называют сочетаниями без повторений.

Число всевозможных сочетаний из из n элементов по m элементов обозначают

Формула для подсчёта числа сочетаний:

Используя данную формулу можно отметить основные свойства сочетаний.

Простейшие свойства сочетаний:

1)

2)

3)

Доказательства свойства сочетаний

1)

2)

3)

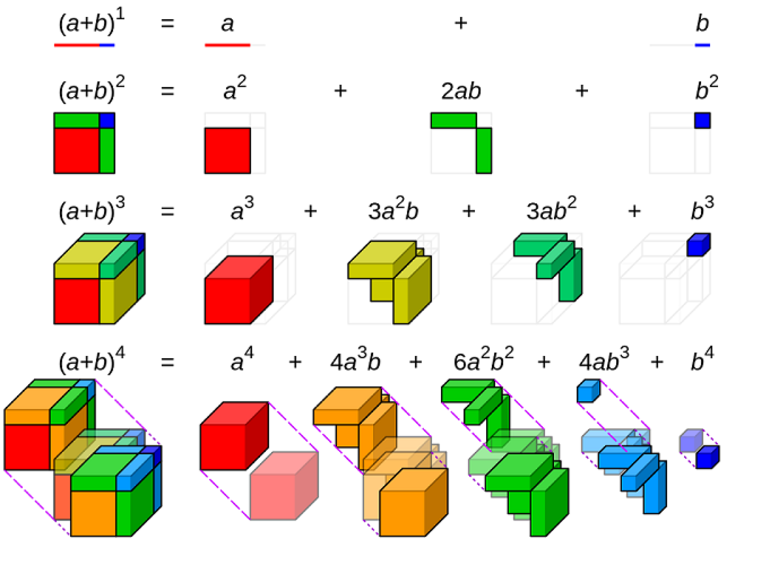
При возведении суммы или разности двух чисел во вторую или третью степень мы пользовались формулами сокращенного умножения, которые являются частным случаем бинома Ньютона.

Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.

Числа являются коэффициентами в формуле бинома Ньютона:

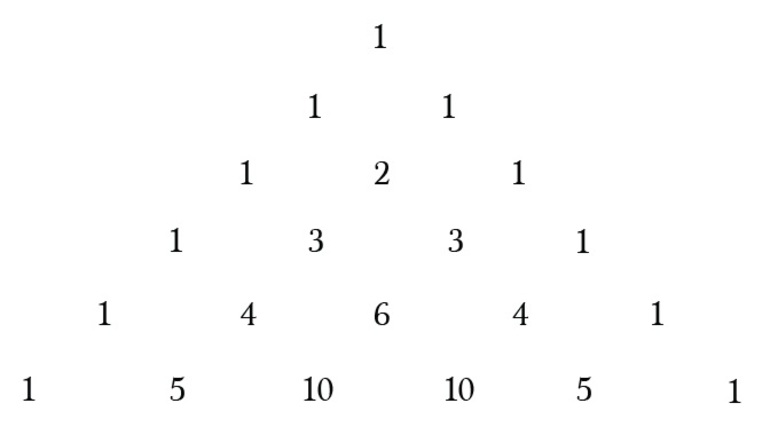
Для более простого подсчета коэффициентов Бинома Ньютона для невысоких степеней удобно пользоваться треугольником Паскаля:

По бокам в каждой строчки имеется коэффициент, равный единице. Все средние коэффициенты считаются, как сумма верхних, которые находятся над ними.

Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.

Не трудно заметить, что строки треугольника симметричны относительно вертикальной оси. Это еще одно замечательное свойство треугольника Паскаля

Исаак Ньютон (1642-1727 гг.) – выдающийся английский ученый, один из создателей классической физики. Биография Ньютона богата во всех смыслах этого слова. Он сделал немало открытий в области физики, астрономии, механике и математике. Ньютон является автором фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.

А при чем же здесь бином Ньютона и биномиальные коэффициенты? Формула

была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени произвольное рациональное число (возможно, отрицательное).

Примеры и разбор решения заданий тренировочного модуля

В вазе лежат двенадцать конфет, четыре из которых шоколадные, а остальные карамель. Вы хотите угоститься, выбрав две шоколадные и три карамельные конфеты. Сколькими способами вы можете это сделать?

Мы имеем два события. Это выбор шоколадных и выбор карамельных конфет. Порядок конфет не важен. Поэтому мы можем использовать формулу сочетания для каждого из событий. Так, как шоколадных конфет всего четыре, а выбрать мы хотим две, то это можно сделать способами .

1)

Теперь посчитаем количество выбора карамельных конфет. Их общее количество в вазе 12-4=8, а выбрать мы хотим три. Рассчитаем сочетание из восьми по три.

2)

События выбора разных видов конфет между собой независимы, поэтому по правилу умножения получаем

3)

Представить разложение двучлена в n степени в виде многочлена, где n=0, 1, 2, …,5

Первые четыре разложения мы хорошо умеем делать, используя формулы квадрата и куба разности.

А для представления бинома четвертой и пятой степени воспользуемся треугольником Паскаля.

Источник

Древние знания

Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.

Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.

Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.

Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.

Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:

К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.

Утверждение теоремы

Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.

Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :

Теорема может быть применена к степеням любого бинома.

С точки зрения геометрии

Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.

Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:

Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.

Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.

Биномные обобщения

Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.

Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.

Короткий путь

Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.

Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).

Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.

Источник

Бином Ньютона — формула, доказательство и примеры решения

Древние знания

Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.

Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.

К VI веку н. э. индийские математики, вероятно, знали способ выразить общее правило, как частное, и выражали это примерно в таком виде: n! / (n — k)!k!. Чёткое его изложение можно найти в тексте XII века, автор которого — Бхаскар. Насколько известно, первая формулировка биноминальной теоремы и соответствующая таблица коэффициентов найдена в работе Аль-Караджи, которая цитируется Аль-Самавалем в его трудах.

Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.

Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.

В 1544 году Майкл Стифель ввёл термин «биномиальный коэффициент» и показал, как его использовать для выражения (1 + a) n с точки зрения (1 + a) n — 1 через «треугольник Паскаля». Блез Паскаль всесторонне изучил треугольник в трактате «Traité du triangle arithmétique» (1653).

Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:

К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.

Утверждение теоремы

Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.

Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :

Теорема может быть применена к степеням любого бинома.

С точки зрения геометрии

Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.

Биномиальные коэффициенты появляются в разложении бинома Ньютона. Обычно их записывают как ( n k) и интерпретируют, как количество способов выбора k элементов из n строки треугольника Паскаля. Коэффициент x n — k y k находят по формуле: ( n k) = n! / k! (n-k)!, которая определяется в терминах факториальной функции n!.

Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:

Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.

Или, например, общий случай. Расширение (x + y) n дает сумму 2 n произведений вида e1 e2 … en, где каждый ei равен x или y. Коэффициенты перестановки показывают, что каждый продукт равен x n — k y k для некоторого k между 0 и n. Для заданного k следующие значения равны по порядку:

Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.

Биномные обобщения

Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.

Однако для произвольного числа r можно вычислить ( r k) = r(r — 1) ··· (r — k + 1) / k! = (r)k / k!, где (·) k является символом Похгаммера, который здесь означает падающий факториал. Это согласуется с обычными определениями. Когда r — неотрицательное целое число, биномиальные коэффициенты при k > r равны нулю, поэтому это уравнение сводится к обычной биномиальной теореме, где существует не более r + 1 ненулевых членов. Для других значений r ряд обычно имеет бесконечно много ненулевых членов.

Обобщения можно распространить на случай, когда x и y — комплексные числа. Для этой версии следует снова принять | х | > | у | и определить степени x + y и x, используя голоморфную ветвь логарифма, определённую на открытом диске радиуса | х | с центром в х. Обобщённая теорема бинома справедлива и для элементов х и у в банаховой алгебре, пока х = ух, х является обратимым, а || у / х || Проверка в действии

Начать лучше с решения простой задачи, которую учитель покажет классу на уроке алгебры. Например, нужно расширить (2x-3) ³. Это было бы не слишком трудно сделать, воспользовавшись онлайн-калькулятором. Но нужно использовать бином, когда придётся столкнуться с более крупными расширениями, такими как двучлены, возведённые в 4, 5, 6, … степени.

Для начала нужно определить два члена из бинома (положения x и y формулы) и степени (буква n), до которой нужно расширить бином. Например, чтобы расширить (2x-3) ³, два члена составляют 2x и -3, а значение мощности (или n) равно 3. Следует отметить, что всякий раз, когда в биноме есть знак вычитания, очень важно помнить, что минус следует использовать только в качестве отрицательного символа в сопутствующем термине.

Замечательная вещь в теореме о биноме — это то, что она позволяет найти расширенный многочлен без умножения множества биномов вместе. Довольно интересное свойство. Оказывается, что число слагаемых в искомом расширенном полиноме всегда будет на единицу больше, чем сила, которую расширяют. Это означает, что необходимо создавать многочлен с четырьмя членами, так как мощность в этом примере равна 3.

Каждый член будет иметь (2x) и (-3), а также формулу «n выбирает k», где n = 3. Нужно записать это 4 раза, по одному на каждый член, оставив значение k в «n выбирает k». На этом этапе подсчёта значения степеней не заполняются.

Далее нужно заполнить k-значения и полномочия. Здесь можно следовать формуле суммирования, увеличивая мощность для каждого члена. Но довольно просто следовать шаблонам. Значения k в «n выбирает k» начинаются с k = 0 и увеличиваются на 1 в каждом члене. Последний член должен заканчиваться на n, равный k, в этом случае n = 3 и k = 3. Затем нужно добавить полномочия на (2x) и (-3).

Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.

Короткий путь

Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.

Теперь хорошая часть. В Треугольнике Паскаля спрятаны все ответы — это настоящая шпаргалка. Диаграмма ниже показывает, где находятся скрытые «n выбирает k».

Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).

Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.

Источник