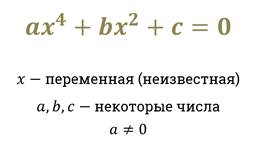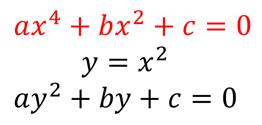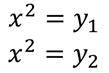что такое биквадратное уравнение и как его решать

Биквадратные уравнения. Уравнения приводимые к квадратным

Урок 21. Подготовка к ОГЭ по математике 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Биквадратные уравнения. Уравнения приводимые к квадратным»

· повторить алгоритм решения уравнений, приводимых к квадратным;

· вспомнить, какие уравнения называются биквадратными.

Мы уже с вами вспоминали, какие уравнения называются квадратными и как решать квадратные уравнения с помощью дискриминанта или теоремы Виета.

Также рассматривают так называемые биквадратные уравнения. Частичка би означает два, то есть биквадратное уравнение можно понимать, как квадратное в квадратном.

Звучит не очень понятно, но на самом деле – все просто.

Биквадратным называется уравнение вида:

Обратите внимание, здесь переменная или выражение с переменной появляются только в четвертой и второй степени, это особенность таких уравнений.

Биквадратное уравнение введением новой переменной приводится к квадратному уравнению.

Решая это уравнение, находим корни квадратного уравнения. Возвращаясь к замене, мы получим в зависимости от корней квадратного уравнения или ни одного, или одно или два квадратных уравнений. Решения этих уравнений и будут решениями исходного биквадратного уравнения.

Теперь давайте вспомним, что:

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Рассмотрим ещё один пример.

Итак, давайте теперь сформулируем алгоритм решения уравнений, сводящихся к квадратным в целом и решения биквадратных уравнений в частности.

Сегодня на уроке, мы рассмотрели алгоритм решения уравнений, приводимые к квадратным, вспомнили какие уравнения называются биквадратными. Рассмотрели несколько примеров.

Источник

Биквадратные уравнения — примеры с решениями

Впервые с решением биквадратных уравнений сталкиваются на уроках алгебры. Степенные равенства высокого порядка решаются по аналогии с квадратными уравнениями. Существует несколько способов, позволяющих найти ответ, но чаще используется метод введения новой переменной. Такой подход простой и разобраться с ним будет под силу даже семикласснику. При этом существуют и онлайн-сервисы, проводящие вычисление корней квадратичного равенства.

Появление методики

Уравнения начали составлять ещё в Древнем Вавилоне. Это было вызвано потребностью находить площади земельных участков, выполнять инженерные работы. Составляли равенства и астрономы, высчитывая расстояния до обнаруживаемых космических тел. Квадратные равенства встречаются в клинописных текстах греков и вавилонян. При этом в этих записях попадаются уравнения, содержащие кубическую или биквадратную степень.

Несмотря на довольно хорошее развитие алгебры в стародавнее время, находимые упоминания о равенствах содержат только ответы, без указаний способов решений. Задачи с примерами решения биквадратных уравнений встречаются у астронома Ариабхатта и индийского учёного Брахмапутра. Формулы для решения сложных уравнений были изложены в сборнике «Книга абака», написанной в 1202 году итальянцем Фибоначчи. Это издание способствовало развитию математики, в частности, алгебре, в Италии, Германии, Франции. Большой вклад в развитие теории решения внесли и советские учёные-математики: Чеботарев, Четаев.

В XVI веках в Китае был разработан способ нахождения корней равенств высшей степени методом Цинь Цзю-шао, после успешно применявшимся в работах Руффини и Горнера.

Этот метод использовал способ подбора, но применим был только для случаев, когда в ответе присутствовали только целые числа.

Все способы решения биквадратных уравнений сводились к приведению их к простому квадратному равенству. Была найдена формула, позволяющая решать уравнения с помощью радикалов (корней). Впервые этот метод предложил Виета, но он был рассчитан только на положительные ответы. Итальянские же учёные Тарталья, Кордано, Бомбелли стали учитывать и отрицательные корни. В итоге Декарт, Жирар и Ньютон привели способы решения к современному виду.

Биквадратные выражения стали разделять на полные и неполные. В алгоритмическом языке корнями уравнения начали называть такие значения неизвестной составляющей, при которой решаемое выражение обращается в правильное числовое равенство. То есть чтобы решить задачу, нужно найти всевозможные его корни или доказать, что решения быть не может.

Основные понятия

Биквадратным уравнением будет называться равенство вида: a*p 4 + b*p 2 + c = 0. Переменные a, b, c могут быть различными числами, при этом A не должно равняться нулю. Символ C называют свободным членом. За P принимают неизвестную переменную, требующую вычисления. Решение уравнений сводится к поиску чисел, которые при подстановке вместо P сделают равенство верным.

Так как значения с1, с2… Cm — это все возможные корни f, то для любого поля будет верным: f (p) = (c — c1) * (c — c2)…(c — cm) * s (p). Учитывая, что s (p) не равно нулю, а f (p) = 0 только в том случае, если C равно некоторому числу I, величина корней многочлена f не может быть более значения m.

Таким образом, уравнение может иметь четыре, три, два, или одно решение. При этом есть вероятность, что ответа может совсем и не быть. Принцип, по которому решаются биквадратные уравнения, следующий:

Квадратные уравнения можно решать любым удобным способом. Типичная схема состоит всего из четырёх шагов и редко вызывает трудности понимания. Пожалуй, сложности могут возникнуть только при нахождении комплексных корней.

Решение равенств

Без знания методов нахождения корней в квадратных уравнениях решить самостоятельно биквадратное равенство не удастся, так как исходное неравенство в итоге приводится к виду квадратичного. Существует несколько способов, позволяющих быстро найти нужные корни или доказать невозможность существования равенства.

К основным относят:

Разложение многочлена на множители основано на группировании и нахождении дискриминанта, то есть знака, по виду которого можно судить о существовании корней. Для решения используется формула: a * p 2 + b * p + c = a * (p — p 1) * (p — p 2), где p и являются корнями уравнения. Этот способ понятен и используется при обучении учащихся решению задач такого типа.

Существуют специальные формулы нахождения корней квадратного, а значит, и биквадратного уравнения. Выглядят они следующим образом: p 1 = (- b — (b 2 — 4 ac) ½ ) / (2* a) и p 2 = (- b + (b 2 + 4 ac) ½ ) / (2* a). С их помощью можно решить любое уравнение. При этом часто для упрощения решения вводят замену подкоренному выражению (b 2 — 4 ac) обозначая его буквой D — дискриминант. Если D больше нуля, то есть два корня, если меньше — решений нет. Если же D = 0, то существует только один корень.

Франсуа Виет, проводя математические исследования, смог обнаружить зависимость между корнями уравнения и его коэффициентами. Он установил, что если p1 и p2 являются решениями равенства, то их сумма будет равна второму коэффициенту с другим знаком, а произведение свободному члену. То есть для уравнения вида: p2 +r*p + k = 0, будет справедливо записать, что p1 + p2 = — r, p1 * p2 = k.

Примеры уравнений

Разложение на множители

Самостоятельная работа, дающаяся в школе, часто предполагает решение биквадратных равенств методом разложения на множители. Связанно это с тем, что этот способ позволяет понять принцип нахождения корней для многочлена любой степени.

Пошагово описать разложение многочлена можно на следующем примере: p 4 + 2p 3 + 3p 2 + 4p +2. Решают его в следующей последовательности:

Вычисление корней требует внимательности и усердия. Для проверки своих навыков можно использовать онлайн-калькуляторы. Это сервисы, использующие специальное программное обеспечение, часто написанное на Паскале, умеют быстро и безошибочно рассчитывать корни любого примера.

Чтобы решить биквадратное уравнение онлайн, особых умений или знаний правил не нужно. Всё, что требуется — это ввести в предложенную форму параметры решаемого равенства. Из наиболее популярных интернет-порталов выделяют Allcalc. Используя его, можно проверить свои знания, исправить допущенные ошибки при самостоятельном расчёте. Причём свои услуги сайт предлагает совершенно бесплатно.

Источник

Биквадратные уравнения и его корни

Ищем педагогов в команду «Инфоурок»

Конспект урока алгебры в 8 классе.

Тема – «Биквадратное уравнение и его корни».

образовательная: дать определение биквадратного уравнения, научиться решать биквадратные уравнения, исследовать число корней биквадратного уравнения;

воспитательная: формировать умение работать в группах, выслушивать мнение товарища, доказывать свою точку зрения;

развивающая: развивать навыки самостоятельной и исследовательской работы.

Тип урока: изучение и первичное закрепление новых знаний.

Форма урока: урок-исследование.

1. Организационный момент.

2. Актуализация знаний.

3. Открытие детьми темы урока (кроссворд).

4. Постановка детьми целей урока.

5. Самостоятельная работа.

6. Итог самостоятельной работы.

7. Пример решения биквадратного уравнения.

10. Итоги исследования.

— Здравствуйте, ребята! Начинаем урок. Сегодня на уроке вы будете исследователями, свои исследования будете проводить в группах. Желаю вам удачи, хорошего настроения и взаимопонимания! Девизом урока пусть будут слова Л. Н. Толстого «Ум человеческий только тогда понимает общения, когда он сам его сделал или проверил».

— В начале для разминки выполним устные упражнения:

6 – х = 0

— Какое уравнение лишнее? (лишнее уравнение . 1, 2 и 4 уравнения – квадратные)

-Как называется первое уравнение? ( неполное квадратное )

-Назовите способ решения ( вынесение общего множителя )

— Как называется второе и четвертое уравнения ( приведенное квадратное уравнение )

-Назовите способ решения ( по теореме Виета ). Сформулируйте теорему.

— Для того чтобы узнать как называется третье уравнение, давайте разгадаем кроссворд.

Третья степень числа. ( Куб )

Подкоренное выражение в формуле корней квадратного уравнения. ( Дискриминант )

Значение переменной, обращающее уравнение в верное равенство. ( Корень )

Уравнения, имеющие одинаковые корни. ( Равносильные )

Равенство с переменной. ( Уравнение )

Квадратное уравнение, с первым коэффициентом равным нулю. ( Приведенное )

Многочлен в правой части квадратного уравнения. ( Трехчлен )

Равенство, содержащее числа и переменные. ( Формула )

Французский математик. ( Виет )

Один из видов квадратного уравнения. ( Неполное )

Множество корней уравнения. ( Решения )

— Прочитайте слово, которое получилось в выделенной горизонтальной строке.

(Биквадратное). Третье уравнение называется биквадратным.

— Теперь вы можете сказать, какова тема нашего урока.

( Тема урока «Биквадратное уравнение»). Открываем тетради, записываем число, тему урока.

— Какие цели мы можем поставить перед собой на урок? У вас на столах есть цветные треугольники, на них вы напишите цели, какие вы определяете для своей группы на данный урок и в этом вам поможет список целей для любого урока.

Каждая группа озвучивает свои цели, прикрепляет на доске.

— Переходим к работе, работа с учебником по определенному плану.

План самостоятельной работы:

Прочитайте определение БУ (учебник № 435, стр. 110)

Запишите определение в тетрадь

Существенно ли замечание, что а не равно нулю

Разберите решенное уравнение

На листе А-3 распишите алгоритм решения биквадратного уравнения.

Обсудите составленный алгоритм в группе

Дайте сигнал о готовности.

Тому, кто закончит быстрее всех, предложить решить биквадратное уравнение.(№ 435, б)

6. Итог самостоятельной работы.

— Итак, что же вы узнали?

(Биквадратным называется уравнение вида ах 4 + вх 2 + с = 0, где а ≠ 0).

— Существенно ли замечание, что а ≠ 0?

( Да, т.к. если а будет равно 0, то уравнение будет квадратным (неполным)).

— Какой алгоритм решения биквадратного уравнения вы записали?

(Каждая группа проговаривает что они записали и вывешивает на доску).

Для проверки ребятам раздаются правильный вариант АЛГОРИТМА решения уравнения.

Алгоритм решения биквадратного уравнения.

Ввести замену переменной: пусть у 2 =х

Составить квадратное уравнение с новой переменной:

Решить новое квадратное уравнение.

Вернуться к замене переменной.

Решить получившиеся квадратные уравнения

Сделать вывод о числе решений биквадратного уравнения.

— Вы, наверное устали, взбодримся. Группы учащихся становятся друг перед другом в цепочку, взявшись за руки возле доски. В начале цепи, на равном расстоянии стоит ведущий (учитель) и держит за руку участника из каждой цепи.

Все играют молча. Ведущий одновременно сжимает руку каждого участника (подает сигнал). Получив сигнал, он должен сжать руку своему соседу. Таким образом, сигнал передается по всей цепи. Задача, чтобы сигнал быстрее был передан и загорелась лампочка, последний в цепи (поднимает руку).

— Сейчас мы проведём исследование: сколько корней имеет биквадратное уравнение. Каждая группа получит по три уравнение и решает их. А потом мы сделаем выводы о том, сколько корней имеют биквадратные уравнения.( Учитель раздаёт уравнения: х 4 -10х 2 +9=0, 2х 4 –х 2 -1=0, х 4 +5х 2 +4=0, 2х 4 +5х 2 +4=0, х 4 -8х 2 +16=0, х 4 +8х 2 +16=0.)

— Итак, что получилось?

1группа показывает решение у доски.

— х 4 -10х 2 +9=0. У нас получился дискриминант положительный, значит, квадратное уравнение имеет 2 корня, корни тоже положительные, значит всего 4 корня.

— х 4 +5х 2 +4=0. Дискриминант квадратного уравнения положительный, но корни отрицательные, значит, биквадратное уравнение не имеет корней.

— Уравнение х 4 +8х 2 +16=0 не имеет корней, т.к. хотя и Д=0, но корень-то отрицательный.

+ 2х 4 –х 2 -1=0. Дискриминант положительный, один корень положительный, а другой отрицательный, значит, биквадратное уравнение имеет 2 корня.

+ 2х 4 +5х 2 +4=0. А у нас дискриминант отрицательный, поэтому уравнение не имеет корней.

+ Уравнение х 4 -8х 2 +16=0 имеет 2 корня, т.к. квадратное уравнение имеет 1 корень (Д=0).

9. Итог исследования. Из рассмотренных примеров видно, что биквадратное уравнение может иметь четыре, три, два, один действительный корень, но может и не иметь корней. (Биквадратное уравнение может иметь от 0 до 4 решений)

Итоги исследования оформляем в таблицу.

10. Итог урока. Метод «Какой путь прошли?»

-Сегодня на уроке вы самостоятельно разобрались с биквадратными уравнениями. И мы должны подвести итог. ( Каждая группа получает набор бумаги, вырезанной в форме ступни. Задача группы – написать о том, что понравилось, что не понравилось на уроке, достигли ли поставленных целей на урок? После заполнения все ступни вывешиваются на доску и прочитываются).

-Провести исследование может ли БУ иметь ровно 3 корня? 1 корень?

— Почему уравнения такого вида называются биквадратными? Что означает приставка «би» к известному термину «квадратное уравнение»?

1. Третья степень числа.

2. Подкоренное выражение в формуле корней квадратного уравнения.

3. Значение переменной, обращающее уравнение в верное равенство.

4. Уравнения, имеющие одинаковые корни.

5. Равенство с переменной.

6. Квадратное уравнение, с первым коэффициентом равным нулю.

7. Многочлен в правой части квадратного уравнения.

8. Равенство, содержащее числа и переменные.

9. Французский математик.

11. Один из видов квадратного уравнения.

12. Множество корней уравнения.

Список целей урока

Изучить материал модулей.

Составить собственное представление о предлагаемом объекте.

Усвоить основные понятия темы.

Выполнить самостоятельно исследование по данной теме.

Проявить и развить свои способности (назвать их).

Научиться аргументированно спорить, доказывать и опровергать утверждения педагога.

План самостоятельной работы:

Прочитайте определение БУ (учебник № 435, стр. 110)

Запишите определение в тетрадь

Существенно ли замечание, что а не равно нулю

Разберите решенное уравнение

Составьте алгоритм решения этого уравнения и запишите его

Источник

Об уравнениях высших степеней

Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.

Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:

1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.

Кубические уравнения

Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:

Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:

В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.

Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.

Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.

Возвратные кубические уравнения

Возвратные кубические уравнения имеют вид:

Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:

Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Возвратные биквадратные уравнения

Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:

В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:

Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.

А теперь перейдём к примеру:

Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).

Область применения

В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.

Источник