что такое астатическая система что такое порядок астатизма
6.3. Понятие астатизма
Если классифицировать САУ по точности в установившемся режиме, то основным классификационным признаком может служить порядок астатизма 
Порядок астатизма 
Порядок астатизма по входному сигналу 

Системы нулевого порядка астатизма 
Такие системы отрабатывают даже постоянное входное воздействие 

Системы первого порядка астатизма 

Системы второго порядка астатизма 


пример. На рис.6.2 приведена структурная схема системы с астатизмом первого порядка.
Рис.6.2. Система с астатизмом первого порядка
Для этой системы передаточная функция разомкнутой части системы будет иметь вид

Следовательно, передаточная функция для ошибки по задающему воздействию представляется как

разложив это выражение в ряд Тейлора, получим

Отсюда, сравнивая с (6.6) находим коэффициенты ошибок

Из примера видно, что коэффициент 

Допустим, задающее воздействие имеет вид

тогда 

В соответствии с формулой (6.7) и определенными коэффициентами ошибок, установившаяся ошибка системы от задающего воздействия будет равна

Важно отметить, что общий коэффициент усиления 

Аналогичным образом можно определить коэффициенты ошибок и установившуюся ошибку системы по возмущающему воздействию. Необходимо только использовать соответствующую передаточную функцию 
Рассмотрим графики отработки астатической САУ различных входных воздействий.
§ Входное воздействие постоянное 
Рис.6.3. Отработка постоянного входного воздействия
Постоянное входное воздействие САУ отрабатывает без установившейся ошибки.
§ Входное воздействие имеет скоростную составляющую 
Рис.6.4. Отработка скоростной составляющей входного сигнала
входное воздействие, содержащее скоростную составляющую, САУ отрабатывает с постоянной установившейся ошибкой.
§ Входное воздействие имеет составляющую ускорения
Рис.6.5. Отработка ускорения
Из анализа графиков, представленных на рис.6.3 – 6.5 можно сделать следующее заключение. Система автоматического управления, обладающая первым порядком астатизма 








§ 58. Порядок астатизма и способы его повышения
Порядок астатизма – порядковый номер первого отличного от нуля коэффициента ошибки при разложении п.ф. в ряд Маклорена.
2) cистема с астатизмом первого порядка ( = 1):
3) cистема с астатизмом -го порядка:
Применяют четыре основных метода повышения порядка астатизма:
1) Включение интегрирующих звеньев в ОС по данному входному воздействию. Число интегрирующих звеньев в ОС определяет порядок астатизма.
2) Применение неединичной главной ОС.
У 
где 
После подстановки и преобразований можно заметить, что в числитель п.ф. Ф g входят слагаемые с разными знаками. Это дает возможность за счет выбора Wос сделать равными нулю ряд коэффициентов числителя при младших степенях s, и, как следствие, ряд первых коэффициентов ошибок.
Первые два метода влияют на устойчивость, потому что добавляемые звенья входят в основной замкнутый контур и поэтому влияют на коэффициенты характеристического уравнения.
П


П 
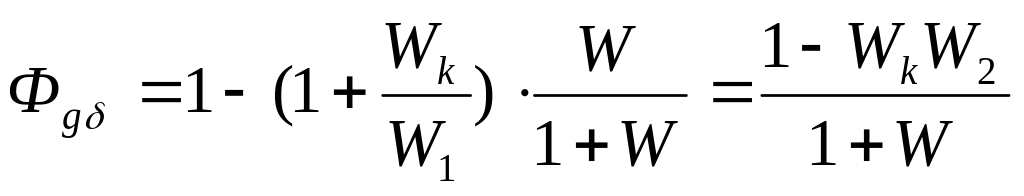
Отсюда видно, что можно повысить порядок астатизма (разный знак слагаемых в числителе) и, в принципе, достичь полной независимости (инвариантности) ошибки от g, если обеспечитьWк= 1/W2 и в итоге Фgδ = 0. Точного равенства нулю добиться обычно нельзя, так как если W2 инерционное, то Wк должно быть идеальным форсирующим звеном, что нереализуемо.
4) Предварительное искажение программы (предискажение).
Идея состоит в том, что инерционная система, реагируя на искаженную программу, может, в принципе, создавать на выходе величину более близкую к истинной программе g. Это искажение обеспечивает фильтр Wф.
Д 

что может служить обоснованием данного метода.
Достоинством методов 3 и 4 является то, что они не влияют на устойчивость, так как вводимые звенья в основной контур не входят.
Что такое астатическая система что такое порядок астатизма
В § 1.6 отмечалось, что качество работы САР характеризуется ошибкой (1.2). Предел, к которому стремится ошибка с течением времени, называется установившейся ошибкой САР:
В том случае, когда все внешние воздействия (задающее и возмущающие) с течением времени стремятся к постоянным значениям, установившаяся ошибка (1.23) называется статической. Ограничимся случаем, когда статическая ошибка
где 




САР называется статической (или обладающей статизмом) по отношению к данному внешнему воздействию, если составляющая статической ошибки (1.24), обусловленная этим воздействием, отлична от нуля. Например, при 





Приведенные определения показывают, что понятия статизма и астатизма связаны с рассмотрением установившегося режима САР и всегда относятся к тому или иному конкретному внешнему воздействию. При этом часто для упрощения все другие внешние воздействия (кроме рассматриваемого) условно полагают равными нулю.
Покажем, например, что система прямого регулирования давления (см. рис. 1.8, а) является статической по отношению к изменению наружного давления 








отношению к изменениям наружного давления. Аналогично доказывается статизм этой системы по отношению к изменениям весового расхода воздуха на входе в резервуар 

Общим для всех перечисленных САР является использование в них пропорционального закона регулирования (1.8), который и обусловливает их статизм по отношению к упомянутым выше возмущениям. Физическая сущность возникновения статической ошибки при регулировании по закону (1.8) предельно проста: для компенсации вредного влияния возмущений необходимо изменить положение регулирующего органа, что возможно лишь при 


Рис. 1.21. Зависимость регулируемой величины от возмущающего воздействия в установившемся режиме: 1 — объект без регулятора, 2 — статическая САР, 3 — астатическая САР
Не следует думать, что из-за наличия статической ошибки статические САР не пригодны для практического применения. В правильно рассчитанной системе статическая ошибка может быть сделана весьма малой и уж во всяком случае значительно меньшей, чем в объекте регулирования без регулятора (зависимость 1 на рис. 1.21). Кроме того, вопросы точности работы в установившемся режиме далеко не исчерпывают всей проблематики теории и практики регулирования.
Не менее важны вопросы поведения САР в динамике, в неустановившихся режимах. Достаточно заметить, что так называемые неустойчивые объекты регулирования (см. гл. 5) вообще не могут работать без автоматических регуляторов.
Приведенный анализ причин появления статической ошибки позволяет сделать вывод о том, что для ликвидации статической ошибки следует изменить закон регулирования, отказавшись от пропорциональной зависимости между регулирующим воздействием и ошибкой.
Для получения астатизма требуется, очевидно, такая связь между 












В том случае, когда САР обладает астатизмом относительно некоторого возмущения 


Что такое астатическая система что такое порядок астатизма
Астатизм первого порядка часто встречается в системах, содержащих исполнительный двигатель электрического, пневматического или гидравлического типа. В простейшем случае, когда канал управления системы состоит из безынерционного усилителя и двигателя любого типа и не содержит корректирующих средств, передаточная функция разомкнутой системы может быть представлена в виде
где 


называть «несимметричными» в отличие от «симметричного» типового перехода оси нуля децибел, свойственного л. а. х., изображенной на рис. 5.14.
Определение допустимого значения постоянной времени 
Исследуя (5.124) на максимум, можно найти условие того, чтобы показатель колебательности не превышал заданного значения:
Рис. 5.16. «Несимметричные» л. а. х. систем с астатизмом первого порядка (типа 1—2 и 1-2-3. ).
Формула (5.125) позволяет при заданном значении добротности по скорости определять допустимое значение постоянной времени двигателя или при заданном значении постоянной времени двигателя — максимальное значение добротности по скорости, которое можно иметь в системе.
В более сложном случае, когда в канале управления имеется ряд инерционных звеньев, формула (5.123) приобретает вид
сумму всех постоянных времени с добротностью по скорости и показателем колебательности аналогично выражению (5.125):
Формула (5.127) дает хорошую точность при 




Рис. 5.17. «Симметричная» л. а. х. систем с астатизмом первого порядка (тип 1-2- 1-2-3-. ).
Л. а. х. типа 1—2—1—2 — 3. соответствует передаточная функция разомкнутой системы
Обычно сопрягающая частота 
фазе. Это будет тем справедливей, чем больше необходимое значение добротности по скорости. Поэтому с большой степенью точности здесь могут быть использованы формулы предыдущего параграфа, дающие связь между общим коэффициентом усиления 
В рассматриваемом здесь случае положение всей л. а. х. определяется значением базовой частоты (рис. 5.17)
В соответствии с формулами (5.113) и (5.121) имеем
или в соответствии с формулами (5.115) и (5.122)
При более точном расчете можно учесть дополнительный запас по фазе (по сравнению с системой, имеющей астатизм второго порядка)
Это обстоятельство позволяет немного увеличить допустимую сумму постоянных времени Топределяемую формулами (5.120) или (5.121), или немного уменьшить требуемое значение постоянной времени 
При этом постоянная времени 
Рис. 5.18. «Несимметричная» л. а. х. статической системы (тип
























