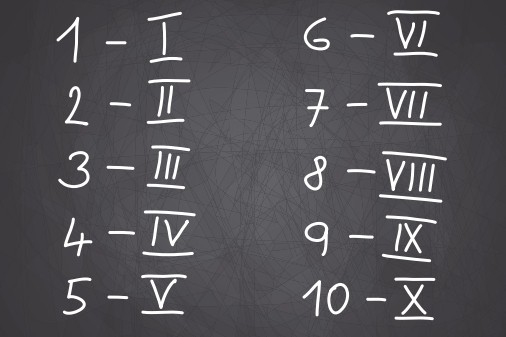Цифра внизу числа что значит
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 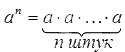
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Таблица степеней
Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.
Калькулятор степеней
С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».
Таблица степеней от 1 до 10
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
10 10 = 10000000000
Теория
запись читается: «a» в степени «n».
4 6 = 4 × 4 × 4 × 4 × 4 × 4 = 4096
Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.
Что означают последние 2 цифры в паспорте внизу после галочки?
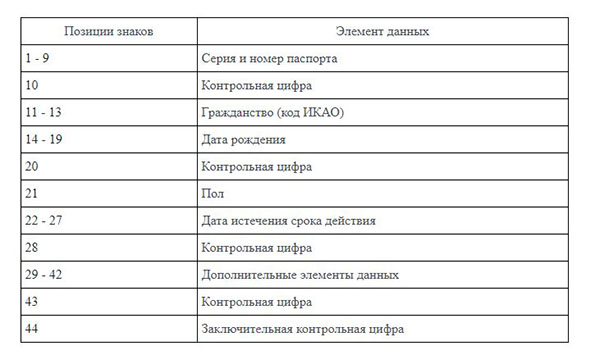
Для многих номер паспорта скрывает в себе какую-то магию: по какой логике высчитываются эти цифры. Почему тому или иному человеку достаются именно те числа, которые он получил, что означают последние две цифры в паспорте внизу после галочки и влияют ли они на что-либо? В действительности, номер паспорта вычисляется не случайно, а для этого существует специальная формула, которая утверждена на законодательном уровне. И каждая цифра в паспорте взята не с потолка, а высчитана по этой закономерности. Кроме того, она несёт в себе какой-то смысл и значение. И ничего скрытого и секретного в этом нет.
В этой статье разбираем значение последних 2 цифр в нижней строке номера паспорта после символа меньше «
Значение последней цифры нижней строки номера паспорта
Последняя цифра является одним из контрольных чисел. Контрольное число, как понятно по названию, необходимо для контроля за правильностью всех введённых данных.
Контрольные числа используются во многих областях, кроме паспорта они бывают и на других документах, а также применяются не только в обороте документов. Они помогают защитить большое количество данных от случайных ошибок. В паспорте ошибки недопустимы. Особо широкое распространение контрольные числа получили в компьютерной области, где они используются для проверки правильности файлов и называются биты чётности, код Рида-Соломона и CRC.
И, конечно же, последние цифры в нижней строке номера паспорта не являются количеством людей с таким же именем. Об этом говорят многие, но это не правда.
Как контрольные числа помогают минимизировать риск ошибок?
Рассмотрим на простом примере. Представьте себе несложный массив данных, состоящий, допустим, из даты рождения гражданина — 9 августа 1980 года, даты выдачи документа — 25 мая 2015 года, кода органа, который выдал документ — 475. На первый взгляд эти цифры кажутся простыми, но из-за человеческого фактора они могут быть где-то введены неверно. А если данные документа ввести неверно, то возможны серьёзные последствия.
Теперь, если придумать какую-то формулу для этих цифр, по которой будет высчитываться контрольное число. И всем эту формулу рассказать, то все смогут очень просто проверять правильность этих данных — достаточно просто посмотреть на контрольное число, а не сверять все параметры.
Приведём пример использования контрольного числа. Берём заданную дату рождения 090880, дату выдачи 250515 и номер органа 475. Если умножить каждое число, допустим, на 5, то получаем: дата рождения 045040400, дата выдачи 1025025525, и номер органа 203525. А теперь, если сложить полученные произведения, то имеем 45 040 400 + 1 025 025 525 + 203 525 = 1 070 269 450. И делим это число, например, на 800, результат будет 1 337 836,8125. И условимся, что контрольным числом будет то, что остаётся после запятой, после указанных вычислений. Получается 8125.
Кто будет это всё считать?
Конечно же, это делается не вручную, а с помощью специальной программы, которая имеется везде, где требуется проверка документов (например, в паспортом столе, в банке, на таможне). Поэтому нижняя строка паспорта называется машиночитаемой строкой — компьютер видит номера, высчитывает их по заранее заданной известной формуле. Получает контрольное число, и сравнивает его с тем, что написано в документе. На всё уходит меньше секунды. Надеюсь значение последних 2 цифр в паспорте внизу после галочки больше не будут вводить вас в заблуждение.

Контрольное число помогает, если ошибка в документе была случайной. Но от злонамеренных подделок документа это не спасает.
Подробнее о машиночитаемой строке внизу паспорта вы можете узнать в этом видео.
Формула расчёта контрольного числа паспорта
Выше был приведён пример того, как может высчитываться контрольное число и последние 2 цифры в паспорте. Это был простой пример для того, чтобы стала понятна технология. Однако эта цифра в паспорте определяется более сложной формулой и включает в себя больше параметров, чем было представлено в нашем примере. Так, формула контрольного числа паспорта использует такие данные:
Кроме этого, в формуле применяются несколько контрольных чисел, которые высчитываются из некоторых из описанных данных, а затем из них уже определяется итоговое контрольное число, которое и записывается в нижней строке номера паспорта после символа меньше «
Формулу расчёта контрольного числа паспорта регулирует Приложение N 8 к Административному регламенту Министерства внутренних дел Российской Федерации по предоставлению государственной услуги по выдаче, замене паспортов гражданина Российской Федерации, удостоверяющих личность гражданина Российской Федерации.
В частности, в документе приводится такой пример расчёта:
Кроме того, в приложении можно познакомиться с более сложным примером:
Чем число отличается от цифры?
Число и цифра — это разные понятия. Нередко мы говорим: «Приведем такие цифры», понимая под этим именно числовые данные. Неправильно было бы говорить: «В этом случае цифры больше», имея в виду, например, объемы производства или продажи товара, потому что это численные показатели. Хотя, конечно, слово «цифры» может употребляться для обозначения числовых данных, но только в множественном числе.
Что же такое число? Это абстрактная сущность, которую используют для определения количественной характеристики объектов. Число возникло еще в глубокой древности и стало основным понятием математики. Например, говорят о натуральных числах, четных и нечетных, даже о мнимых.
А цифра — это только знак для отображения чисел. Цифр всегда ограниченное количество. Например, арабские (точнее, индийские) цифры, которыми мы пользуемся, это 0, 1, 2, 3,4, 5, б, 7, 8, 9. Их десять. Из них можно составить бесконечное множество чисел — двух-, трехзначных и т.д.
Надо отличать однозначные числа от многозначных. Например, 5 — это и цифра, и число, а вот 10 — только число, цифрой называть его неправильно.
Для обозначения римских цифр используются буквы I, V, X, L, С, D, М (I — 1, V — 5, X — 10, L — 50, С — 100, D — 500 и М — 1000). Есть и другие системы счисления: двоичная, где используются только две цифры — 0 и 1; восьмеричная, где используются 8 цифр — от 0 до 7; шестнадцатеричная, где используются 16 цифр (к обычным 10 цифрам добавляются 6 первых букв латинского алфавита); двенадцатеричная и шестидесятеричная. Две последние системы придуманы в древнем Шумере и Вавилоне, а сейчас они используются в часах. В двенадцатеричной системе счет велся по фалангам всех пальцев, кроме большого.
Числа составляются из цифр при помощи систем счисления. Они бывают позиционными и непозиционными.
В позиционных системах счисления значение цифры зависит от места расположения, то есть разряда. Например, 15 и 51 — это разные числа, составленные из одинаковых цифр. В первом случае цифра 1 означает десяток, во втором — единицу.
В непозиционной системе счисления значение цифры не зависит от места, где она расположена. Таковой является римская система. Например, в числах IX и XI символ I всегда означает единицу, только в первом случае ее надо вычесть из десятки, а во втором — прибавить к ней. В данном случае система накладывает определенные ограничения на порядок цифр (расположение по возрастанию или убыванию), но позиционной все же не является.
Путешествия цифр
Арабские цифры, в том числе и ноль, на самом деле возникли в Индии не позже V в. Арабы лишь приспособили их к своему письму. Ученый Аль-Хорезми (783—850) успешно использовал эти цифры и даже написал книгу «Об индийском счете», где показал, насколько такая система удобна. Цифры были оценены по достоинству, распространились по всему Арабскому халифату, в том числе во входившей в его состав Испании. Так в X в. они попали в Европу, поэтому за ними утвердилось название арабских.