Целочисленное значение что это
Какие числа называются целыми
Определение целых чисел
Что важно знать о целых числах:
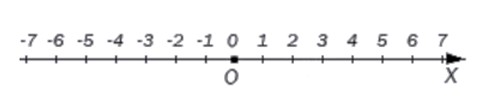
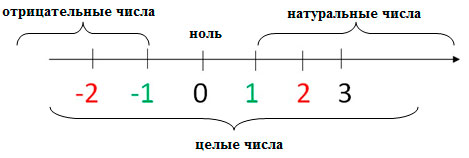
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
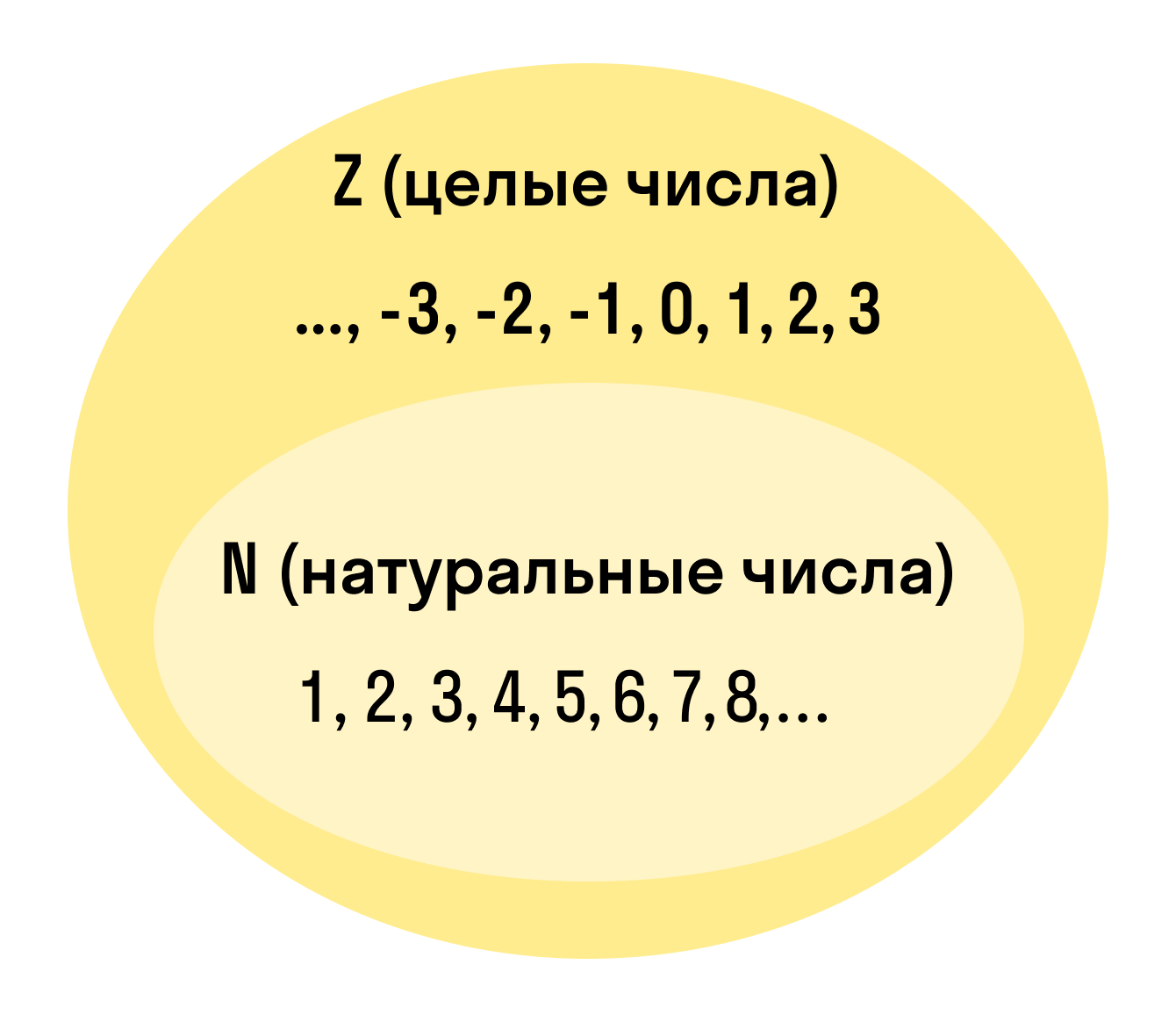
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и противоположные натуральным отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Определение 1. Целые числа
Целые числа и координатная прямая
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Определение 3. Отрицательные целые числа
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Как видим, число нуль не является ни положительным, ни отрицательным.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).
Что такое целые числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о ЦЕЛЫХ ЧИСЛАХ.
Это весьма обширное понятие из математики, с которым школьники сталкиваются уже в 5 классе.
Целые числа — это.
Целые числа – это все положительные, все отрицательные числа и ноль. Главное, чтобы они не содержали дробной части.
Согласно этому определению, к целым числам можно отнести:
и так далее. Ведь у них нет дробной части. А вот числа:
и так далее не могут считаться целыми, так как у них есть какие-то цифры после запятой или они являются дробью.
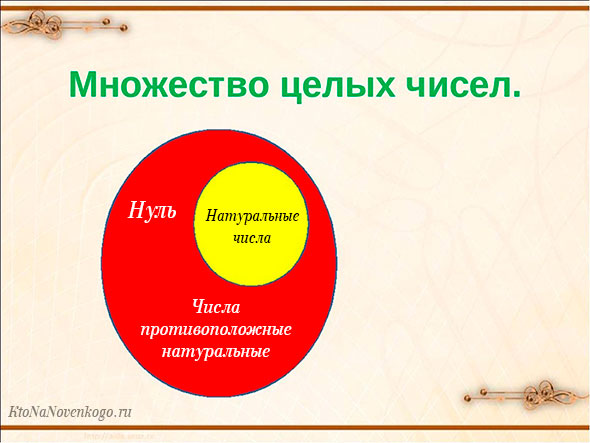
Все многообразие целых чисел называется множеством целых чисел. Это официальный математический термин. И обозначается он буквой Z.
В это множество входят и так называемые натуральные числа (это что?). Это все те, которые имеют положительное значение, но опять же без дробной части. Проще говоря, все числа, которые мы используем при счете. Например, 1, 2, 5, 10, 100 и так далее.
Множество натуральных чисел обознается буквой N. И зависимость его и множества целых чисел наглядно показана на следующем рисунке.
Отсюда можно сделать важный вывод:
Любое натуральное число автоматически является еще и целым. Но при этом далеко не каждое целое число является еще и натуральным.
А можно представить это и в таком варианте. Целые числа — это:
Каким бы определением вы не пользовались, главное, чтобы было все понятно.
История изучения целых чисел
Опять же эту историю нужно разделить на три части. Ведь изучение натуральных чисел, а также открытие нуля и отрицательных чисел происходило независимо друг от друга. Да еще и в разных странах.
Изучение натуральных чисел
Тут все максимально просто. Эти числа возникли, как только человеку понадобилось считать – будь то куски мяса или количество бревен для дома.
Более точное изучение натуральных чисел начинается в Древнем Египте и Древней Месопотамии, а это более 6 тысяч лет назад.
А современные математики опираются на то, что после себя оставил древнегреческий ученый Пифагор. Он как раз активно собирал египетские и вавилонские данные, а после отразил их в своих трудах.
Открытие нуля
Конечно, египтяне, вавилоняне и даже греки знали о существовании нуля. Но не считали его числом, а потому не пользовались им. Это, кстати, приносило им немало сложностей. Они порой часами решали задачки, которые нынешний школьник посчитает за минуту.
Но официально число ноль появилось в 5-м веке. И «изобрели» его в Индии. Дело в том, что у местных жителей всегда существовало убеждение, что «ничто – это тоже что-то». Даже понятие Нирвана, которое обозначает состояние небытие, зародилось именно в Индии.
Потому-то там и придумали символ, который обозначал бы «ничто». Авторами его стали математики Брахмагупта и Ариабхата.
Как видите, индийский символ нуля очень похож на современный. Ну, разве что приплюснут и больше напоминает правильную окружность. Форма выбрана не случайно. По индийским поверьям, ноль символизирует круговорот жизни и мироздания. Его еще называют «змея вечности».
Когда арабы завоевали часть Индии, они переняли все математические знания. А во время крестовых походов многое, в том числе и цифры, перекочевали в Европу. Хотя потребовалось еще несколько сотен лет, чтобы «ноль» стал неотъемлемой частью европейской науки.
Открытие отрицательных чисел
Отрицательные числа первыми начали изучать китайцы во 2 веке до нашей эры. Их использовали в торговле и называли «долгами». А обычные числа – «имуществом». А для записи отрицательных чисел использовали перевернутый вид.
А вот в Европе к ним очень долго относились пренебрежительно, считая «несуществующими» и «абсурдными». Лишь в 12 веке математик Леонардо Фибоначчи (автор знаменитого числового ряда) описал их в своей книге «Книга Абака».
В середине 16 века математик Михаил Штифель посвятил им целый раздел в своей книге «Полная арифметика».
Но признание они получили лишь в 17 веке, после того как известный Рене Декарт создал свою систему координат.
В ней он также использовал нуль, привязав к нему положительные и отрицательные числа. Одни находились справа от него, а другие – слева.
Свойства целых чисел
Всем целым числам свойственны следующие характеристики:
Если А и В – целые, то А+В=целое, А-В=целое и А*В=целое
А + В = В + А, А * В = В * А
Добавим: точно такое же правило действует и при делении. Минус на минус дают плюс. А минус на плюс или плюс на минус всегда дают минус.
Вместо заключения
Мы уже рассказали, с каким трудом в нашу жизнь попали отрицательные числа. Но сегодня они широко используются не только в математике.
Ну и, наконец, слова положительный и отрицательный используются и в более разговорном смысле, как синонимы хорошего и плохого.
Например, в книгах и фильмах обязательно есть положительные и отрицательные герои. Также и наши черты характера, эмоции и поступки можно разделить на эти две категории.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Сами по себе числа ничего не значат, будь они даже целыми и натуральными, чтобы в них был смысл, они должны иметь привязку к чему-либо. Например, единица меньше пятидесяти, но всегда ли единица меньше? Если я скажу, что один рубль меньше пятидесяти копеек, то это будет ложью.
Урок №31. Целочисленные типы данных: short, int и long
Обновл. 11 Сен 2021 |
На этом уроке мы рассмотрим целочисленные типы данных в языке С++, их диапазоны значений, операцию деления, а также переполнение (что это такое и примеры).
Целочисленные типы данных
| Тип | Минимальный размер | |
| Символьный тип данных | char | 1 байт |
| Целочисленный тип данных | short | 2 байта |
| int | 2 байта (но чаще всего 4 байта) | |
| long | 4 байта | |
| long long | 8 байт |
Примечание: Тип char — это особый случай: он является как целочисленным, так и символьным типом данных. Об этом детально мы поговорим на одном из следующих уроков.
Основным различием между целочисленными типами, перечисленными выше, является их размер, чем он больше, тем больше значений сможет хранить переменная этого типа.
Объявление целочисленных переменных
Объявление происходит следующим образом:
Диапазоны значений и знак целочисленных типов данных
Как вы уже знаете из предыдущего урока, переменная с n-ным количеством бит может хранить 2 n возможных значений. Но что это за значения? Это значения, которые находятся в диапазоне. Диапазон — это значения от и до, которые может хранить определенный тип данных. Диапазон целочисленной переменной определяется двумя факторами: её размером (измеряется в битах) и её знаком (который может быть signed или unsigned).
Целочисленный тип signed (со знаком) означает, что переменная может содержать как положительные, так и отрицательные числа. Чтобы объявить переменную как signed, используйте ключевое слово signed :
По умолчанию, ключевое слово signed пишется перед типом данных.
В некоторых случаях мы можем заранее знать, что отрицательные числа в программе использоваться не будут. Это очень часто встречается при использовании переменных для хранения количества или размера чего-либо (например, ваш рост или вес не может быть отрицательным).
Целочисленный тип unsigned (без знака) может содержать только положительные числа. Чтобы объявить переменную как unsigned, используйте ключевое слово unsigned :
1-байтовая целочисленная переменная без знака (unsigned) имеет диапазон значений от 0 до 255.
Обратите внимание, объявление переменной как unsigned означает, что она не сможет содержать отрицательные числа (только положительные).
Теперь, когда вы поняли разницу между signed и unsigned, давайте рассмотрим диапазоны значений разных типов данных:
Для нематематиков: Используем таблицу 🙂
Начинающие программисты иногда путаются между signed и unsigned переменными. Но есть простой способ запомнить их различия. Чем отличается отрицательное число от положительного? Правильно! Минусом спереди. Если минуса нет, значит число — положительное. Следовательно, целочисленный тип со знаком (signed) означает, что минус может присутствовать, т.е. числа могут быть как положительными, так и отрицательными. Целочисленный тип без знака (unsigned) означает, что минус спереди отсутствует, т.е. числа могут быть только положительными.
Что используется по умолчанию: signed или unsigned?
Так что же произойдет, если мы объявим переменную без указания signed или unsigned?
| Тип | По умолчанию | |
| Символьный тип данных | char | signed или unsigned (в большинстве случаев signed) |
| Целочисленный тип данных | short | signed |
| int | signed | |
| long | signed | |
| long long | signed |
Все целочисленные типы данных, кроме char, являются signed по умолчанию. Тип char может быть как signed, так и unsigned (но, обычно, signed).
В большинстве случаев ключевое слово signed не пишется (оно и так используется по умолчанию).
Программисты, как правило, избегают использования целочисленных типов unsigned, если в этом нет особой надобности, так как с переменными unsigned ошибок, по статистике, возникает больше, нежели с переменными signed.
Правило: Используйте целочисленные типы signed, вместо unsigned.
Переполнение
Вопрос: «Что произойдет, если мы попытаемся использовать значение, которое находится вне диапазона значений определенного типа данных?». Ответ: «Переполнение».
Переполнение (англ. «overflow») случается при потере бит из-за того, что переменной не было выделено достаточно памяти для их хранения.
На уроке №28 мы говорили о том, что данные хранятся в бинарном (двоичном) формате и каждый бит может иметь только 2 возможных значения ( 0 или 1 ). Вот как выглядит диапазон чисел от 0 до 15 в десятичной и двоичной системах:
| Десятичная система | Двоичная система |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
Как вы можете видеть, чем больше число, тем больше ему требуется бит. Поскольку наши переменные имеют фиксированный размер, то на них накладываются ограничения на количество данных, которые они могут хранить.
Примеры переполнения
Рассмотрим переменную unsigned, которая состоит из 4 бит. Любое из двоичных чисел, перечисленных в таблице выше, поместится внутри этой переменной.
«Но что произойдет, если мы попытаемся присвоить значение, которое занимает больше 4 бит?». Правильно! Переполнение. Наша переменная будет хранить только 4 наименее значимых (те, что справа) бита, все остальные — потеряются.
Например, если мы попытаемся поместить число 21 в нашу 4-битную переменную:
| Десятичная система | Двоичная система |
| 21 | 10101 |
Число 21 занимает 5 бит (10101). 4 бита справа (0101) поместятся в переменную, а крайний левый бит (1) просто потеряется. Т.е. наша переменная будет содержать 0101, что равно 101 (нуль спереди не считается), а это уже число 5, а не 21.
Теперь рассмотрим пример в коде (тип short занимает 16 бит):
Результат выполнения программы:
x was: 65535
x is now: 0
Что случилось? Произошло переполнение, так как мы попытались присвоить переменной x значение больше, чем она способна в себе хранить.
Для тех, кто хочет знать больше: Число 65 535 в двоичной системе счисления представлено как 1111 1111 1111 1111. 65 535 — это наибольшее число, которое может хранить 2-байтовая (16 бит) целочисленная переменная без знака, так как это число использует все 16 бит. Когда мы добавляем 1, то получаем число 65 536. Число 65 536 представлено в двоичной системе как 1 0000 0000 0000 0000, и занимает 17 бит! Следовательно, самый главный бит (которым является 1) теряется, а все 16 бит справа — остаются. Комбинация 0000 0000 0000 0000 соответствует десятичному 0, что и является нашим результатом.
Аналогичным образом, мы получим переполнение, использовав число меньше минимального из диапазона допустимых значений:
Результат выполнения программы:
x was: 0
x is now: 65535
Переполнение приводит к потере информации, а это никогда не приветствуется. Если есть хоть малейшее подозрение или предположение, что значением переменной может быть число, которое находится вне диапазона допустимых значений используемого типа данных — используйте тип данных побольше!
Правило: Никогда не допускайте возникновения переполнения в ваших программах!
Деление целочисленных переменных
В языке C++ при делении двух целых чисел, где результатом является другое целое число, всё довольно предсказуемо:
Но что произойдет, если в результате деления двух целых чисел мы получим дробное число? Например:
В языке C++ при делении целых чисел результатом всегда будет другое целое число. А такие числа не могут иметь дробь (она просто отбрасывается, не округляется!).
Правило: Будьте осторожны при делении целых чисел, так как любая дробная часть всегда отбрасывается.
Поделиться в социальных сетях:
Урок №30. Размер типов данных
Комментариев: 23
Всем доброго времени суток. Появился такой вопрос: для объявления без знакового числа, для плюсов, обязательно писать unsigned int X, есть ли сокращенная форма по типу uint X?
Может проще для запоминания было сказать, что тип signed (со знаком) использует 1 (старший бит в байте для записи этого самого знака и для самого числа остается 7 бит (это в случае 1-го байта, для 2- байт 15 и т.д.) и в 7 битах можно записать число не больше чем 128.
К примеру 10000000 это отрицательный ноль. 🙂 Но такого не бывает.
Для того, чтоб числа имели дробь при делении целых чисел можно приписать ноль после точкой. Например : 8.0/5.0 = 1.6
Только это уже совсем другая история)
Достаточно поставить точку одному из выражений. Например: 8. / 5 или 8 / 5.
Остальное компилятор сам подставит)
Вообще, с «железным» правилом «Никогда не допускайте возникновения переполнения в ваших программах!» — сильно погорячились. Потому что очень часто переполнение как раз помогает создать более простой и быстрый код.
Например, нужно много раз увеличивать переменную на 1 и циклически прокручивать все значения от 0 до 255. Писать условие «если равно 255, то присвоить 0» — совсем не нужно, это произойдёт само при прибавлении 1 к 255, если используется 1-байтовая беззнаковая.
Другой очень частый пример: вычисление разности двух значений миллисекундного таймера, чтобы замерить период времени. 4-байтовая переменная с таким таймером переполняется каждые 49 суток. Если система работает непрерывно, то такое может случаться. Когда считаем разность (новое значение таймера минус старое) — возможен случай, когда новое значение уже переполнилось (снова пошло с нуля), а старое ещё нет (огромное число). Но когда вычисляется разность, тут снова произойдёт переполнение (из-за того, что получилось отрицательное значение), и эти два переполнения оказывают взаимно компенсирующее действие, как будто их не было вообще. И разность всё равно будет верной. И не надо городить никаких хитрых алгоритмов.
Скорее всего это какой-то очень древний подход. Никогда не слышал подобного в универе.
Потому что это относится к числам с плавающей точкой. У них отдельный бит хранит знак. В целочисленных типах такого нигде (или почти нигде) нет.
unsigned используется для экономии памяти, это же очевидно. Если знак действительно не нужен за счет дополнительно освобожденного бита, можно увеличить диапазон значений в 2 раза, что в некоторых случаях позволит использовать более «экономные» типы данных.
Ну так нужно указывать другой тип переменной(не целое число). Тогда будет дробь.
Забавная история, почему этот урок так важен =)
В игре Civilization есть баг с механикой агрессии и миролюбия. Суть такова, что агрессивность цивилизации измерялась по шкале от 1 до 10. Девятки и десятки были у всяких Чингисханов, Монтесум и Сталиных, а у духовного пацифиста Махатмы Ганди была единичка. И ещё были модификаторы — строй «республика» уменьшает агрессивность на 1, «демократия» — на 2. Соответственно, сразу же, как только индусы открывали Демократию, у Ганди становилась агрессивность −1.
А теперь внимание. Эта переменная была однобайтная и строго неотрицательная(unsigned), от 0 до 255. Соответственно, агрессивность Махатмы Ганди становилась равна 255 из 10. Поэтому, построив у себя демократию, Ганди двигался рассудком, клепал ядрёные бомбы и умножал всех на ноль.
Действительно хороший пример 🙂 С unsigned нужно быть аккуратным.
4.5 – Целочисленные типы данных без знака, и почему их следует избегать
Целочисленные типы данных без знака
В предыдущем уроке (4.4 – Целочисленные типы данных со знаком) мы рассмотрели целочисленные типы со знаком, которые представляют собой набор типов, которые могут содержать положительные и отрицательные целые числа, включая 0.
C++ также поддерживает беззнаковые целочисленные типы. Беззнаковые целочисленные значения – это целые числа, которые могут содержать только неотрицательные значения.
Определение беззнаковых целочисленных значений
Диапазоны значений целочисленных типов без знака
Ниже показана таблица, показывающая диапазоны беззнаковых целочисленных типов:
| Размер / Тип | Диапазон |
|---|---|
| 1 байт без знака | от 0 до 255 |
| 2 байт без знака | от 0 до 65 535 |
| 4 байт без знака | от 0 до 4 294 967 295 |
| 8 байт без знака | от 0 до 18 446 744 073 709 551 615 |
Диапазон беззнаковой переменной размером n бит составляет от 0 до (2 n )-1.
Целочисленные типы без знака хорошо подходят для сетей и систем с небольшим объемом памяти, когда нет необходимости в отрицательных числах, поскольку беззнаковые целочисленные значения могут хранить бо́льшие положительные числа, не занимая дополнительной памяти.
Напоминание относительно значений со знаком и без знака
Начинающие программисты иногда путаются между значениями со знаком и без знака. Простой способ запомнить разницу: чтобы отличить отрицательные числа от положительных, мы используем знак минус. Если знак не указан, мы предполагаем, что число положительное. Следовательно, целочисленное значение со знаком (целочисленный тип со знаком) может различать положительные и отрицательные числа. Целочисленное значение без знака (целочисленный тип без знака) предполагает, что все значения положительны.
Переполнение целочисленных значений без знака
Что произойдет, если мы попытаемся сохранить число 280 (для представления которого требуется 9 бит) в 1-байтовом (8-битном) целочисленном значении без знака? Ответ – переполнение.
Примечание автора
Как ни странно, в стандарте C++ прямо говорится, что «вычисление с использованием беззнаковых операндов никогда не может переполниться». Это противоречит общему мнению программистов о том, что целочисленное переполнение охватывает случаи как со знаком, так и без знака. Учитывая, что большинство программистов рассмотрело бы этот случай как переполнение, мы будем называть его переполнением, несмотря на утверждения C++ об обратном.
Если значение без знака выходит за пределы допустимого диапазона, оно делится на число, превышающее на единицу наибольшее число, допустимое для заданного типа данных, и сохраняется только остаток.
Число 280 слишком велико, чтобы поместиться в наш 1-байтовый диапазон от 0 до 255. Значение, которое на 1 больше максимального числа для этого типа данных, равно 256. Следовательно, мы делим 280 на 256, получая остаток 24. Остаток 24 – это то, что в итоге сохранится.
Вот еще один способ размышления о том же. Любое число, превышающее наибольшее число, которое может быть представлено заданным типом данных, просто «оборачивается» (или совершает циклический переход). Число 255 находится в диапазоне 1-байтового целочисленного типа, поэтому 255 сохранится нормально. А число 256 находится за пределами диапазона, поэтому оно оборачивается до значения 0. 257 оборачивается до значения 1. 280 оборачивается до значения 24.
Давайте посмотрим на это, используя 2-байтовые целые числа:
Как вы думаете, каким будет результат работы этой программы?
Приведенный выше код в некоторых компиляторах вызывает предупреждение, поскольку компилятор обнаруживает, что целочисленный литерал выходит за пределы допустимого диапазона для данного типа. Если вы всё равно хотите скомпилировать этот код, временно отключите параметр «Treat warnings as errors» (обрабатывать предупреждения как ошибки).
В качестве отступления.
Многие заметные ошибки в истории видеоигр произошли из-за поведения циклического перехода целочисленных значений без знака. В аркадной игре Donkey Kong невозможно пройти уровень 22 из-за бага переполнения, из-за которого у пользователя недостаточно бонусного времени для завершения уровня.
Споры по поводу чисел без знака
Многие разработчики (и некоторые крупные компании, например, Google) считают, что разработчикам следует избегать целочисленных типов без знака.
Во многом это связано с двумя типами поведения, которые могут вызывать проблемы.
На машине автора эта, казалось бы, невинно выглядящая программа дает следующий результат:
Во-вторых, непредвиденное поведение может возникнуть при смешивании целочисленных значений со знаком и без знака. В приведенном выше примере, даже если один из операндов ( x или y ) будет со знаком, другой операнд (беззнаковый) приведет к тому, что операнд со знаком будет преобразован в целочисленное значение без знака, и будет получено такое же поведение!
Рассмотрим следующий фрагмент:
Если вам нужно защитить функцию от отрицательных входных данных, используйте вместо этого утверждение или исключение. Они оба будут рассмотрены позже.
Начинающие программисты часто используют целочисленные типы без знака для представления неотрицательных данных или для того, чтобы воспользоваться дополнительно расширенным диапазоном. Бьярн Страуструп, разработчик C++, сказал: «Использование unsigned int вместо int для получения еще одного бита для представления положительных целых чисел почти никогда не бывает хорошей идеей».
Предупреждение
Избегайте использования числовых типов без знака, за исключением особых случаев или, когда это необходимо.
Не избегайте отрицательных чисел с помощью беззнаковых типов. Если вам нужен больший диапазон, чем предлагает числовой тип со знаком, используйте один из целочисленных типов гарантированной ширины, показанных в следующем уроке (4.6 – Целочисленные типы фиксированной ширины и size_t ).
Если вы всё же используете беззнаковые числа, по возможности избегайте смешивания чисел со знаком и без знака.
Так где же стоит использовать беззнаковые числа?
В C++ всё же есть несколько случаев, когда можно (или необходимо) использовать беззнаковые числа.
Во-первых, числа без знака предпочтительнее при работе с битами (рассматривается в главе O (это заглавная буква «о», а не «0»).
Во-вторых, использование беззнаковых чисел всё еще неизбежно в некоторых случаях, в основном тех, которые связаны с индексацией массивов. Подробнее об этом мы поговорим в уроках по массивам и индексированию массивов.
Также обратите внимание, что, если вы разрабатываете для встраиваемой системы (например, Arduino) или какого-либо другой системы с ограничениями процессора/памяти, использование чисел без знака более распространено и приемлемо (а в некоторых случаях неизбежно) по соображениям производительности.