любой простой силлогизм имеет что

08.12.202316.04.2022 admin 0 Comments

Логика. Тест 13

Поможем успешно пройти тест. Знакомы с особенностями сдачи тестов онлайн в Системах дистанционного обучения (СДО) более 50 ВУЗов. При необходимости проходим систему идентификации, прокторинга, а также можем подключиться к вашему компьютеру удаленно, если ваш вуз требует видеофиксацию во время тестирования.

Закажите решение теста для вашего вуза за 470 рублей прямо сейчас. Решим в течение дня.

1. «Солнце» – это понятие:
единичное
физическое
астрономическое
общее
нулевое

2. Понятие, большее по объему, называется:
родовым
единичным
общим
нулевым
видовым

3. Определение: «Экзистенциализм – это философское направление ХХ в., в котором рассматриваются различные экзистенциальные вопросы и проблемы», – является:
круговым
философским
узким
широким
двусмысленным

4. Отношения между понятиями изображаются:
круговыми схемами Эйлера
круговыми схемами Бэкона
круговыми схемами Пейджера
круговыми схемами Бойлера

5. Деление понятия раскрывает его:
объем
значение
смысл
форму
содержание

6. Связь между субъектом и предикатом вывода в простом силлогизме выполняет:
средний термин
старший термин
больший термин
младший термин
меньший термин

7. В делении: «Люди бывают мужчинами, женщинами, спортсменами и танцорами», – допущена ошибка:
подмена основания
учетверение терминов
скачок в делении
двусмысленность
поспешное обобщение

8. Дедуктивные умозаключения называются:
силлогизмами
алогизмами
софизмами
логицизмами
парадоксами

9. Индукция – это:
вид умозаключения
закон логики
вид дедукции
логическая связка
сложное суждение

10. Дедукция – это движение мысли от:
общего к частному
единого к общему
простого к сложному
сложного к простому
эмпирических данных к теоретическому обобщению

11. Любой простой силлогизм имеет:
фигуру
форму
размер
объем
содержание

12. Сорит – это разновидность:
простого силлогизма
неполной индукции
трудноразрешимого софизма
сложного суждения
логического парадокса

13. Эпихейрема – это:
разновидность умозаключения
правило силлогизма
закон дедукции
раздел индукции
вид сложного суждения

14. Рассуждение: «Докажем, что три раза по два будет не шесть, а четыре. Возьмем спичку или палочку и сломаем ее пополам. Это один раз два. Потом возьмем одну из половинок и ее тоже сломаем пополам. Это второй раз два. Затем возьмем оставшуюся половинку и ее тоже сломаем пополам. Это третий раз два. Итак, три раза по два будет четыре, а не шесть», – является:
софизмом
силлогизмом
антиномией
апорией
парадоксом

15. Найдите частноутвердительное суждение:
Некоторые люди знают французский язык.
Некоторые люди не видели солнечное затмение.
Большинство людей не знают английский язык.
Все люди смертные.
Некоторые преступления не являются преднамеренными.

Источник

Урок 7. Силлогизмы

Этот урок будет посвящён многопосылочным умозаключениям. Так же как и в случае однопосылочных умозаключений, вся необходимая информация в скрытом виде будет присутствовать уже в посылках. Однако, поскольку посылок теперь будет много, то способы её извлечения становятся более сложными, а потому и добытая в заключении информация не будет казаться тривиальной. Кроме того, нужно отметить, что существует много разных видов многопосылочных умозаключений. Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.

Содержание:

Простой категорический силлогизм

Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.

В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).

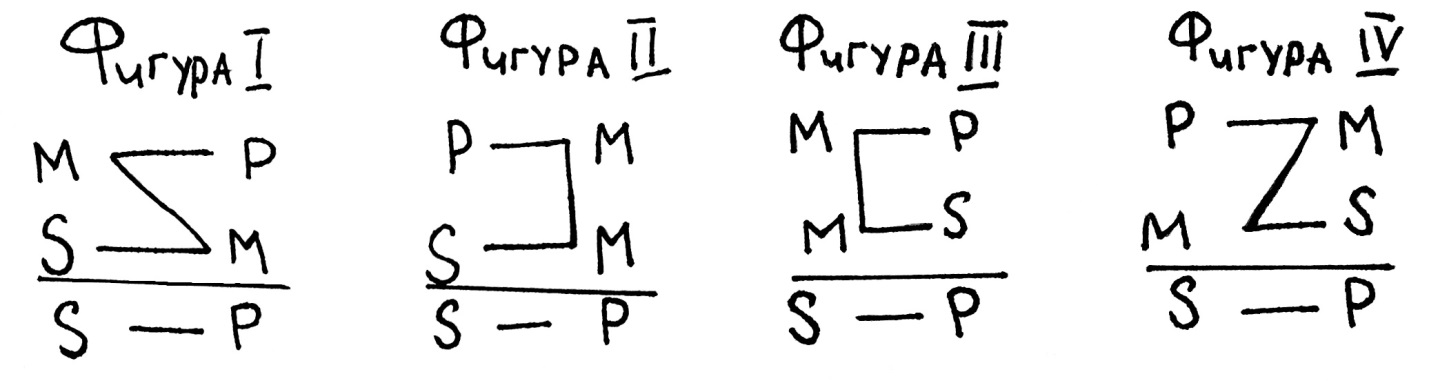
Естественно, в рассуждении посылки могут находиться в любой последовательности. Однако для удобства проверки правильности силлогизмов, большую посылку ставят всегда первой, а меньшую – второй. Тогда в зависимости от расположения терминов все простые категорические силлогизмы можно разделить на четыре вида. Эти виды называются фигурами.

Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.

Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.

Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:

Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.

Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:

К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:

Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.

Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.

Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:

Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.

Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.

Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.

Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:

Правила терминов

Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:

Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:

Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно. Проблема в том, что в этом примере опять произошло учетверение терминов. Вроде бы этот силлогизм содержит три термина. Меньший термин – «”Отцы и дети” Ивана Тургенева». Больший термин – «книги, которые нельзя прочитать за целую жизнь». Средний термин – «книги из собрания Российской государственной библиотеки». Если же присмотреться внимательно, то станет ясно, что субъектом первой посылки является не термин «книги из собрания Российской государственной библиотеки», а термин «все книги из собрания Российской государственной библиотеки». В данном случае «все» – это не квантор общности, а часть субъекта, так как это слово употребляется не в разделительном смысле (каждый в отдельности), а в собирательном (все вместе). Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.

Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.

Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».

Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.

Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.

Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не может перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.

Энтимемы

Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.

Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.

Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.

Теперь располагаем известную нам информацию в форме силлогизма:

В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:

Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:

Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.

Сориты

Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.

Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.

8. Амос Джадд любит холодную баранину.

Над чертой находятся посылки, под чертой – заключение.

Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:

1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.

Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.

Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:

Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:

Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:

Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:

Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:

Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.

Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.

Задачи Эйнштейна

Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Упражнения

Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.

Упражнение 1

Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.

Упражнение 2

Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.

Упражнение 3

Найдите заключения следующих соритов.

Упражнение 4

Проверьте правильность следующих энтимем.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Источник

3.3. Простой, или категорический силлогизм

Рассмотренные в предыдущем параграфе дедуктивные умозаключения также называются силлогизмами. Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все суждения, входящие в него (две посылки и вывод), являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.

Рассмотрим пример простого силлогизма.

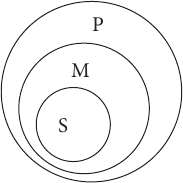
Все цветы (М) – это растения (Р).

Все розы (S) – это цветы (М).

Все розы (S) – это растения (Р).

Обе посылки и вывод являются в данном силлогизме простыми суждениями (причем и посылки, и вывод – это суждения вида А (общеутвердительные)). Обратим внимание на вывод, представленный суждением: Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы возможно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

1. Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).

2. Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма (первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родовидового подчинения), в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.

3. Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М, потому что «средний» на латинском – это medium.

Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т. е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

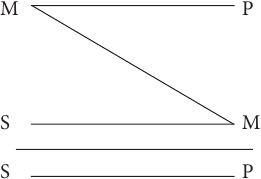
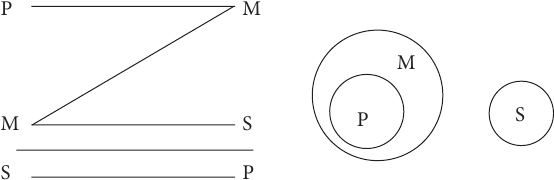
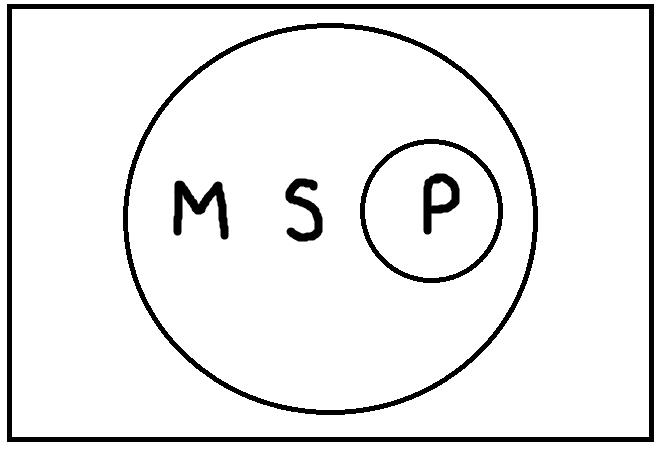
Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

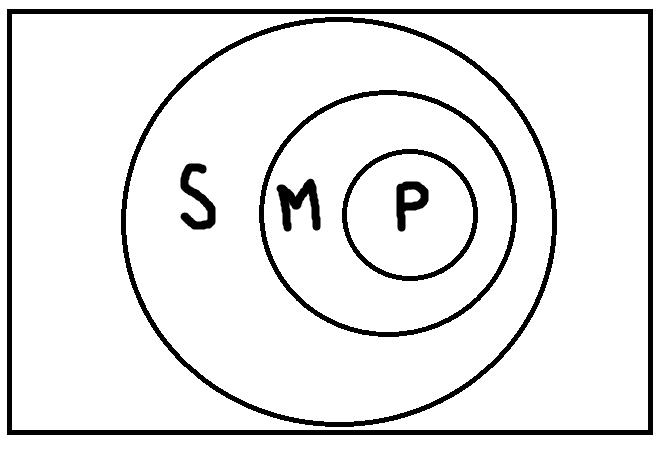
Все газы (М) – это химические элементы (Р).

Гелий (S) – это газ (М).

Гелий (S) – это химический элемент (Р).

Учитывая то, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере:

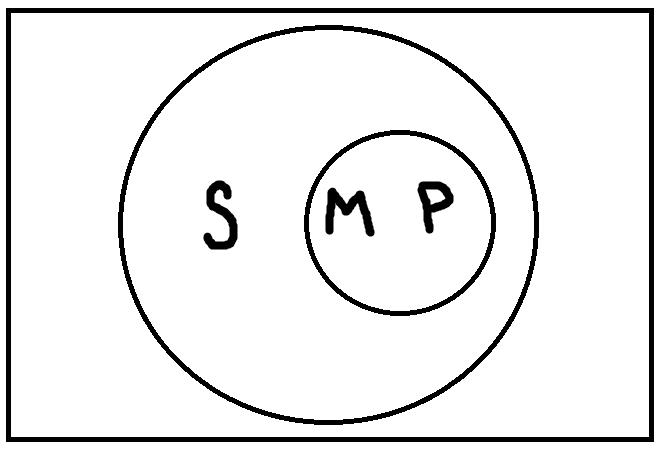
Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, можно изобразить отношения между тремя терминами с помощью кругов Эйлера. В данном случае получится следующая схема:

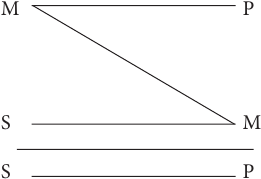
Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:

Все рыбы (Р) дышат жабрами (М).

Все киты (S) не дышат жабрами (М).

Все киты (S) не рыбы (Р).

Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так:

Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

Все тигры (М) – это млекопитающие (Р).

Все тигры (М) – это хищники (S).

Некоторые хищники (S) – это млекопитающие (Р).

Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма:

Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:

Все квадраты (Р) – это прямоугольники (М).

Все прямоугольники (М) – это не треугольники (S).

Все треугольники (S) – это не квадраты (Р).

Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма:

(Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими).

Любой простой силлогизм состоит из трех суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырех видов (А, I, Е, О). Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма. Например, в силлогизме:

Все небесные тела движутся.

Все планеты – это небесные тела.

Все планеты движутся.

Первая посылка является простым суждением вида А (общеутвердительным), вторая посылка – это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус ААА. Силлогизм:

Все журналы – это периодические издания.

Все книги не являются периодическими изданиями.

Все книги не являются журналами.

имеет модус АЕЕ. Силлогизм:

Все углероды – простые тела.

Все углероды электропроводны.

Некоторые электропроводники – простые тела.

имеет модус ААI. Всего модусов во всех четырех фигурах, т. е. возможных комбинаций простых суждений в силлогизме, – 256. В каждой фигуре 64 модуса. Однако из всех этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность ее выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.

Наша задача – уметь определять фигуру и модус любого простого силлогизма. Например, требуется установить фигуру и модус силлогизма:

Все вещества состоят из атомов.

Все жидкости – это вещества.

Все жидкости состоят из атомов.

Прежде всего надо найти субъект и предикат вывода, т. е. меньший и больший термины силлогизма. Далее следует установить местоположение меньшего термина во второй посылке и большего в первой. После этого можно определить средний термин и схематично изобразить расположение всех терминов в силлогизме:

Все вещества (М) состоят из атомов (Р).

Все жидкости (S) – это вещества (М).

Все жидкости (S) состоят из атомов (Р).

Как видим, рассматриваемый силлогизм построен по первой фигуре. Теперь надо найти его модус. Для этого следует выяснить, к какому виду простых суждений относится первая посылка, вторая и вывод. В нашем примере обе посылки и вывод являются суждениями вида А (общеутвердительными), т. е. модус данного силлогизма – ААА. Итак, предложенный силлогизм имеет первую фигуру и модус ААА.

Вывод простого силлогизма является истинным, конечно же, в том случае, когда истинны его посылки. Однако, истинность посылок – это не достаточное условие истинности вывода. Вполне может быть так, что обе посылки в силлогизме истинны, а вывод его ложен. Например:

Все дети обладают мышлением.

Все взрослые – это не дети.

Все взрослые не обладают мышлением.

В этом силлогизме, построенном по первой фигуре, и имеющим модус АЕЕ, и первая, и вторая посылки являются истинными суждениями, из которых вытекает ложный вывод. Почему так получается? Потому что при построении силлогизма следует обращать внимание не только на то, чтобы посылки были истинными, но и, в не меньшей степени, на то, чтобы были соблюдены определенные требования или правила его построения. Рассмотрим еще один пример:

Все нравственные заповеди надо соблюдать.

Законы государства не являются нравственными заповедями.

Законы государства не надо соблюдать.

Данный силлогизм также построен по первой фигуре и имеет модус АЕЕ. В нем из истинных посылок вытекает ложный вывод из-за нарушения правил простого силлогизма, которые будут рассмотрены далее.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Онлайн портал info.epubbooks.ru