логика это что в философии
Что такое ЛОГИКА – зачем она нужна. Виды логики
Логика. Не каждый человек задумывался о том, что такое логика. Хотя логическое мышление присутствует в жизни повсеместно от простых бытовых дел до решения сложных математических задач. Оно неотделимо от науки и творчества, повседневных диалогов и решения насущных дел.
Логика – что это?
Этот термин имеет древнегреческие корни. Он образован от древнегреческого слова «логос», что понимают, как слово, рассуждение, мысль, смысл или разум. Самое простое определение логики – это наука о правильном мышлении, здравомыслии. Она зародилась примерно в V в. до н.э. благодаря трудам философа и мыслителя Аристотеля, который и считается основателем традиционной логики.
Существуют и другие толкования:
Зачем нужна логика?
Основной целью логического мышления является изучение определенной последовательности событий, явлений или действий, их взаимосвязи. То есть человек с помощью разума накапливает имеющиеся знания, аккумулируя их из разных источников, и строит причинно-следственные связи. Индивид руководствуется не своим эмпирическим опытом, а достоверными фактами.
Разобравшись с тем, что такое логика, можно сделать вывод о ее необходимости для:
Виды логики
Благодаря сохранившимся историческим документам доподлинно известно, что логика как наука о законах и формах мышления зародилась примерно 2500 лет назад. С тех пор она претерпевала определенные изменения, которые привели к выделению трех основных видов логики:
Формальная логика
Самым древним считается раздел философии под названием формальная, формально-фактическая или дискретная логика, отцом которой и был знаменитый Аристотель. Он рассматривал эту науку как возможность восприятия и оперирования формальными фактами и связями между ними без учета содержания. Выясняя, какие проблемы решает формальная логика, отметим, что она проверяет правильность рассуждений в современном мире. Важно абстрагироваться от конкретики и учитывать только общую форму суждения или вопроса.
Простым примером можно назвать констатацию факта: «на улице тепло и сухо, поэтому я пойду и прогуляюсь». Такой тип мышления заложен в каждом человеке, ведь впервые видя собеседника, индивид оценивает его внешний вид и подмечает другие особенности, складывая пазл в единую картину. Если же увиденное не соответствует принятым стандартам, то шаблон ломается.
Математическая логика
В начале XIX в. традиционная формальная теоретическая логика пополняется арсеналом математических методов с использованием искусственных языков. Так сформировалась символическая или современная логика, как ее принято называть. Математический подход позволил вывести способность к рассуждению ученых в разных областях науки на новый уровень,
Такая модель упрощает процесс познания благодаря замене слов привычного языка, которые могут нести двусмысленность и неточность, формальными символами. Многие проблемы, которые изучает математическая логика, невозможно сформулировать привычными словесными выражениями с использованием известных методов. Нередко такую науку в более широком плане причисляют к металогике или метаматематике.
Диалектическая логика
Немецкий философ Гегель и последователи марксистской материалистической теории основатели так называемую диалектическую логику, базой для развития которой стала дискретная логика. В ее основе лежит метод руководства не только формой, но и содержанием явлений, объектов и процессов. То есть такая наука о познавательной деятельности может рассматривать не отдельные противоположности, а их связь и схожесть между собой. У этого раздела философии существуют свои законы и принципы:
Законы логики
Как и в любой науке, здесь существуют определенные правила. Закон логики – это принцип, которому необходимо следовать, чтобы из истинных суждений получить правильный вывод. Их разработал и сформулировал еще Аристотель, изучая формальную логику, в которой использовались словесные суждения. Существует четыре базовых закона, нарушение которых приводит к появлению умышленных или неумышленных ложных выводов:
Закон тождества
Изучая, что такое наука логика, непременно сталкиваются с ее первым законом тождества или равенства. Некоторые именуют его принципом постоянства. Суть состоит в том, что на всем протяжении логического рассуждения изначальное понятие должно сохранять свой первоначальный смысл. Искажение, которое свойственно многим языкам и двойственность, многозначность, могут привести к ложным выводам.
Примером несоблюдения этого принципа является простой диалог:
Закон непротиворечия
Еще одним фундаментальным постулатом является закон непротиворечия. Его суть состоит в том, что два противоположных высказывания не могут быть одновременно истинными. Одно или оба из них обязательно окажутся ложными. Можно привести простой пример иллюстрации этого закона:
Закон исключенного третьего
Нередко студенты изучая, что такое наука логика, путают предыдущий закон с принципом исключенного третьего. Они схожи, но суть каждого все же отличится. Этот закон сформулирован так, что истинным может быть либо само суждение, либо же его отрицание. Третьего не дано. То есть закон оперирует не противоположными понятиями, а противоречащими друг другу. К примеру:
Закон достаточного основания
Четвертый закон – логического мышления, был сформулирован не Аристотелем, а лишь в XVIII в. озвучен Готфридом Лейбницем. Суть принципа состоит в том, что любой тезис будет иметь силу только тогда, когда будет подтвержден аргументами. Причем они должны быть такими, чтобы исходная мысль четко вытекала из них.
Самым ярким и знаменитым примером применения закона достаточного основания в жизни является принцип так называемой презумпции невиновности:
Как развить логику?
Многие философские термины и примеры могут показаться обывателю сложными и мало применимыми в обычной жизни. Однако каждый из указанных выше законов мы часто неосознанно можем встретить в любом споре или диалоге, когда собеседники, стремясь ввести друг друга в заблуждение, сознательно или неосознанно их нарушают. Навыки того, как развить логическое мышление, могут пригодиться каждому индивиду для достижения успехов в разных сферах науки и жизни.
Логическое мышление закладывается у человека в раннем возрасте, а умение мыслить абстрактно формируется примерно в 7-8 лет и развивается всю жизнь. Для качественного и полноценного его развития нейропсихологи советуют:
Логика: предикатная, формальная и сентенциальная. Кванторы и возникновение информатики
1 | Введение
Логика, как эпистемологический инструмент, — исследующий знание как таковое, — изобретена независимо в трёх отдельных государствах: Греции (Аристотелем), Китае (до правления Цинь Шихуанди) и Индии. В последних двух государствах логика не распространилась настолько, чтобы получить полноценное развитие. В античной же Греции логика сформировалась в своих основах столь определённо, что дополнилась только через 2 тысячелетия.
Значительные изменения в греческую логику, помимо Буля, Моргана и Рассела, внёс Фреге — самая важная фигура основателей формальной семантики. Он разработал логику предикатов и 2 вида кванторов, попытавшись создать «логически совершенный язык» о котором мечтал Лейбниц. Значимой личностью является также Гёдель, который открыл знаменитые две теоремы о неполноте, описывающие невозможность объединения множества доказуемых утверждений со множеством истинных. Он утверждал, что доказательства математики зависят от начальных предположений, а не фундаментальной истины, из которой происходят ответы. Одна из главных идей его работ состоит в том, что ни один набор аксиом, — в том числе математических, — не способен доказать свою непротиворечивость.
На этом этапе некоторые заметят влияние платонизма на австрийского логика. Совершенно верно, ведь Гёдель не раз заявлял о влиянии метафизики Платона на собственную деятельность. Но сам Платон развитию формальной логики способствовал лишь косвенно: в истории он вносит вклад в развитие другого направления — философской логики. Платоном созданы вопросы, на которых основывается вся западная академическая философия вплоть до наших дней. Философия, в том виде, котором она известна, возникла только благодаря учителю Аристотеля.

В другие периоды в логику также вносили дополнения:
античной школой стоицизма введены термины «модальности», «материальной импликации», «оценки смысла и истины», которые являются задатками логики высказываний;
также средневековыми схоластами введены несколько понятий;
Но главное, что сами логические операции не изменились. «Органон» Аристотеля, как сборник из 6 книг — первоисточник, где подробно описаны главные логические законы. «Органон» (с древнегреческого ὄργανον), означает — инструмент. Аристотель считал, что логика является инструментом к познанию. Он объединяет методом получения информации такие науки:
Физика — наука о природе;
Метафизика — наука о природе природы;
Биология — раздел физики, наука о жизни;
Психология — раздел физики, наука о душе;
Кинематика — раздел физики, наука о движении;
2 | Терминология
У каждой из наук должен быть идентичный фундамент в способе получения гнозисов (знаний), который позволит упорядочить информацию и вывести новые силлогизмы (умозаключения). Только таким образом получится прогресс в познании истины. Без логики наука была бы похожа на коллекционирование фактов, ибо информация бы не поддавалась анализу.
Сам Аристотель находит логике как средству убеждения иное применение: в риторике, спорах, дебатах, выступлениях и т.д., описывая это в труде «Риторика». В западной философии принято давать чёткие определения перед рассуждениями, поэтому определимся с терминами. Логика — наука о правильном мышлении.
В языковой зависимости возникают трудности трактовки термина «наука», но даже в оригинальном названии труда Фридриха Гегеля «Наука логики» — «Wissenschaft der Logik», употребляется слово «наука» (Wissenschaft). Поэтому придём к консенсусу и будем считать, что научной можно назвать ту дисциплину, в которой возможны открытия, исследование и анализ. Логика в таком случае — наука, ибо внутри неё возможно совершать открытия. Яркий пример — комбинаторика Лейбница.
Слово «правильный» веет нормативными коннотациями: правильное поведение, правильное выражение лица, и т.д. Перечисленное соответствует некоторым критериям и логика выставляет их (критерии) для правильного мышления.
Слово «мышление» понимается на интуитивном уровне, но чёткое объяснение затруднительно, обширно и иногда не объективно.

3 | Формальная и неформальная логика
Первоначально, деление логики происходит на формальную и неформальную. Формальная логика отличается тем, что, в отличие от неформальной, записывается уравнениями. Неформальная же логика пишется выражениями в форме языка, поэтому она подходит для риторики, а формальная логика для абстрактных наук.
Формальная логика равным образом делится на дедуктивную и индуктивную. Они различаются тем, что в дедуктивном аргументе истинность условий гарантирует истинность умозаключения или вывода. В индукции же, при истинности условий одинаково возможен ложный и истинный вывод.
Законы формальной логики:
1. Закон тождества (А = А): эквивокация или двусмысленность недопустимы. Нельзя подменять одно понятие, другим.
2. Закон непротиворечия (А ∧ ¬А = 0): одно и то же утверждение не может быть истинным и ложным одновременно.
3. Закон исключения третьего или бивалентности (А ∨ ¬А = 1): утверждение может быть либо истинным, либо ложным — третьего не дано.
Принципы формальной логики:
1. Принцип достаточного обоснования: достаточными являются такие фактические и теоретические обоснования, из которых данное суждение следует с логической необходимостью.
4 | Сентенциальная логика (алгебра высказываний)
Базовые операции сентенциальной логики — логики высказываний, где заглавная буква означает предложение:
Отрицание (Утверждение ¬A истинно тогда и только тогда, когда A ложно): если имеем утверждение «А» и имеем утверждение «не А», то, когда утверждение «А» будет истинным — утверждение «не А» будет ложным. Также и когда утверждение «А» будет ложным — утверждение «не А» будет истинным.
Конъюнкция (Утверждение A ∧ B истинно, если и A, и B — истинны. Ложно в противном случае): в английском языке — союз «and/&»; в русском — «и». В утверждении «А и В», между «А» с «В» стоит знак конъюнкции — «∧». Утверждение «А и В» является истинным, если «А» с «В» являются истинными одновременно. Если хоть один элемент ложен, то всё утверждение ложно. «А и В» подразумевает, во-первых: истинность «А», во-вторых: истинность «В».
Дизъюнкция (Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны — утверждение ложно): в английском языке — союз «or»; в русском — «или». Существует два типа дизъюнкции — включающая и исключающая (в логике используется включающее «или»). Условия таковы, что утверждение «А или В» будет истинным, когда один или оба элемента истинны, но никогда — когда оба элемента ложны. Это противоречит нашему обыденному мышлению, т.к. когда спрашивают: «Чай или кофе?» мы выбираем один элемент, но в логике подразумевается выбор не только одного, а нескольких возможных.
Импликация (Утверждение A ⇒ B ложно, только когда A истинно, а B ложно): в английском языке — «therefore»; в русском языке — «следовательно». Подразумевает истинность одного элемента при истинности другого. Потому что условия истинности соблюдаются всегда, кроме случая, когда «А» истинно, а «B» ложно. Поэтому утверждение: «А» ложно, следовательно «B» ложно — истинно. Покажется, что когда «А» ложно, а «В» истинно — не соблюдаются условия, но это не так. Если вы скажете, что после дождя промокните — это утверждение будет истинным вне зависимости от того, пошёл дождь или нет.
Эквивалентность (Утверждение A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны): если истинно утверждение «А, следовательно В» и истинно утверждение «В, следовательно А», то истинными являются выражения «А эквивалентно В» и соответственно «В эквивалентно А». Условия истинности соблюдаются в случаях, когда оба элемента истинны или оба ложны.
Значение переменных
5 | Предикатная логика первого порядка
В XX веке, после добавлений в область логики работ Лейбница и Фреге, на основе этой дисциплины создаётся новая — информатика. Программирование сохраняет преемственность с видоизменённой логикой Аристотеля — предикатной логикой, описательная способность которой выше, чем у логики высказываний (сентенциальной).
Прежде чем разобрать этот новый тип логики, поговорим об её отличии от сентенциальной. Главная особенность предикатной логики, что заглавными буквами обозначаются предикаты, а не целые высказывания. Можно сказать, что предикат — это математическая функция, которая «накладывает» множество субъектов на множество утверждений.
Высказывание «Я пошёл в зоопарк» — состоит из субъекта и предиката. В нём субъект — «Я», а предикат — то, что остаётся кроме субъекта («пошёл в зоопарк»). Субъект — тот, кто совершает действие в предложении или имеет выраженное свойство; предикат — всё оставшееся. Таким образом, если в сентенциальной логике высказывание «Я пошёл в зоопарк» выражалось бы одной заглавной буквой, то в логике предикатов использовались бы две буквы (заглавная и подстрочная): «P» — для предиката; «x» — для субъекта. Субъекты обозначаются переменной («x»), потому что в предикатной логике появляются две относительно новые операции: универсальный и экзистенциальный кванторы. Особенность кванторов заключается в том, что ими возможно записать выражение истинное при всех возможных переменных «х» или хотя бы при одном.
Универсальный квантор (квантор всеобщности) обозначается символом — «∀», с указанием переменной под ним. Возьмём утверждение «Все пингвины чёрно-белые». В логике высказываний оно бы выражалось как «X ⇒ P», где «X» — нечто являющееся пингвином, а «P» — нечто являющееся чёрно-белым. В предикатной логике же используются субъекты и предикаты, поэтому нечто являющееся пингвином (субъект), обозначалось бы переменной «х» снизу под предикатом. «»х» — является пингвином, следовательно, является чёрно-белым». Записывается так: P(х) ⇒ B(х), где P(х): х — пингвин; B(х): x — чёрно-белый.
Однако этого недостаточно, ведь непонятно, один субъект «х» чёрно-белый или больше одного, а может вообще все. Поэтому утверждение «»х» — является пингвином, следовательно, является чёрно-белым», берётся в скобки и перед скобками используется символ «∀» с переменной «х» под ним — которые вместе и будут универсальным квантором.
Универсальный квантор переводится как: «Для всех «х» истинно, что …». Теперь утверждение «х — является пингвином, следовательно, является чёрно-белым» с универсальным квантором перед ним, расшифровывается так: «Для всех «х» истинно, что «х» — является пингвином, следовательно, является чёрно-белым». Это означает, что чем бы ни был объект во вселенной, если этот объект пингвин — он является чёрно-белым. Полная запись будет выглядеть так:
Экзистенциальный квантор (квантор существования) обозначается символом — «∃» с указанием переменной под ним. Возьмём утверждение «Некоторые пингвины серые». Как и в прошлый раз, выражение «»x» — является пингвином и «х» — является серым» возносим в скобки и ставим перед ними квантор, в этом случае экзистенциальный с указанной переменной. «»x» — является пингвином и «х» — является серым» записывается так: P(х) ∧ C(х), где P(х): х — пингвин; C(х): x — серый.
Экзистенциальный квантор можно перевести так: «Есть такой «х», для которого будет истинно, что …». Подразумевается, что есть как минимум один «х», для которого выполняются условия выражения. Если вам говорят, что ДНК не существует, достаточно показать одну молекулу дезоксирибонуклеиновой кислоты для опровержения этого утверждения. Также и с кванторами, если существует хотя бы один серый пингвин, то утверждение об отсутствии серых пингвинов будет ложно. Полная запись экзистенциального квантора для выражения «Есть такой «х», для которого будет истинно, что «x» — является пингвином и «х» — является серым», будет выглядеть так:
6 | Заключение
Примечательно, что есть возможность перевода одного вида квантора в другой. Возьмём утверждение «Все пингвины не являются серыми». Для универсального квантора текстовая запись будет такая: «Для всех «х», будет истинным утверждение о том, что если «х» — является пингвином, то «х» — не является серым объектом». Но утверждение изменяется и для экзистенциального квантора, используя знак отрицания: «Нет такого «х», для которого бы было истинным утверждение о том, что «x»— является пингвином и «х»— является серым».
В середине XIX века, Готлоб Фреге дополнил логику Аристотеля двумя этими операциями, которые позже сформировались в отдельную дисциплину — предикатную логику. С введением в логику экзистенциального квантора (после универсального) — предикатная логика, в основе своей, завершилась как система…
Источники:
1 — Аристотель: «Органон» — «Первая аналитика» и «Вторая аналитика»;
2 — Аристотель: «Риторика»;
3 — Готлоб Фреге: «Исчисление понятий»;
4 — «Monatshefte für Mathematik und Physik» 1931 г.: Курт Гёдель «О принципиально неразрешимых положениях в системе Principia Mathematica и родственных ей системах»;
5 — The Early Mathematical Manuscripts of Leibniz;
6 — Мельников Сергей: «Введение в философию Аристотеля»;
7 — Гильмутдинова Нина: «Логика и теория аргументации»;
Логика — это основа и законы правильного мышления
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В течение дня самого обычного человека посещает тысячи мыслей. Мы думаем о реальных объектах и явлениях, о гипотетических ситуациях (кто победит, если Годзилла сразится с Кинг-Конгом?).
Но все мысли формируются одними и теми же способами по определенным принципам. Логика как раз изучает формы, методы и законы мышления.
Что такое логика?
Этот термин имеет греческие корни. Он образовался от слова «логос», что переводится как «рассуждение, разум, мысль, смысл». Это не случайно, ведь основы современной логики заложил древнегреческий философ Аристотель.
Толковый словарь Даля дает определение: «логика — это наука здравомыслия, наука о том, как правильно рассуждать». Ее основной задачей является поиск пути перехода от предпосылок к выводу, получение достоверного знания о предмете исследования.
На самом деле, интуитивное понимание логики впитывается в нас с молоком матери. Маленький ребенок рассуждает: «Если не слушаться родителей, можно понести наказание». С детства мы учимся строить свои высказывания правильным образом, делать верные выводы, поступать логично – адекватно ситуации.
Толковый словарь Ожегова предлагает 3 значения для слова «логика»:
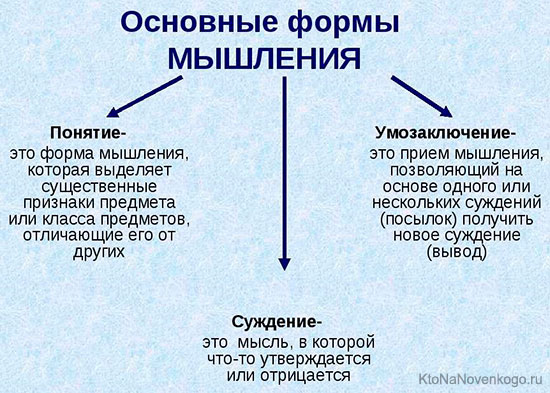
Основы логики — формы логического мышления
Форма мышления – это оболочка для наших мыслей, способ по которому они строятся.
Существует всего 3 формы:
Все бесконечное пространство мыслей выражается этими тремя формами.
В нашей голове хранятся миллиарды понятий, которые мы объединяем в суждения, а потом делаем из них умозаключения. И все за доли секунды, даже не осознавая этого.
Законы логики (логического познания)
Законы логики — это принципы, следуя которым из истинных суждений можно гарантированно извлечь правильный вывод.
Существуют 4 закона. Порой их нарушают случайно, тогда получается ошибочное умозаключение — паралогизм. Иногда специально, с целью запутать собеседника и подвести его к ложной мысли. Тогда возникают софизмы – недостоверные выводы, которые кажутся логически правильными.
Закон тождества
Для тех, кто прогуливал в школе математику, уточню: тождество — это равенство.
Звучит закон так: понятие должно сохранять свой изначальный смысл на всем протяжении логического рассуждения.
Язык — многогранен, почти у любого слова есть несколько смыслов. Если в процессе подменить одно значение другим, получится ложный логический вывод.
Покажу на примере известной шуточной загадки: «Зачем вода в стакане?». Конечно, чтобы ее выпили. Но нет, она за стеклом. Тут как раз идет игра смыслов, нет тождества (однозначности). Понятия нельзя смешивать понятия и обязательно нужно избегать двусмысленности.
Закон непротиворечия
Два высказывания, которые несовместимы друг с другом, не могут быть одновременно истинными. Одно из них — ложное, а, возможно, и оба.
Вот Вася говорит, что Петя украл яблоко. Петя утверждает, что это сделал Вася. Эти высказывания противоречат друг другу. Значит, они не могут быть одновременно истинными. Но оба утверждения способны оказаться ложными, если есть третий вариант — на самом деле яблоко просто упало и закатилось под стол.
Логические противоречия бывают:
Контактные противоречия сразу бросаются в глаза, а вот дистантные отследить сложно. Например, неопытный оратор начинает речь с одной идеи, потом путается и в конце сам себя опровергает.
Закон исключенного третьего
Если из двух суждений одно является отрицанием другого, то они не могут быть одновременно ложными. Хотя бы одно должно быть истинным.
Этот закон тесно связан с предыдущим. Они похожи, но есть разница. Здесь рассматриваются высказывания, отрицающие друг друга («А» и «не А»), а не противоречия.
Вот пример: Вася говорит, что Петя украл яблоко. Петя утверждает, что он этого не делал. Тут нет никакого третьего варианта, одно из высказываний должно быть истинным. Это и есть пример использования закона исключенного третьего.
Закон достаточного основания
Всякое утверждение, чтобы считаться истинным и справедливым, должно быть доказано. Подтверждение можно получить эмпирическим (опытным) или теоретическим способами.
Вот ученый заявляет, что есть элементарные частицы, которые могут двигаться быстрее скорости света. Но никто не поверит, пока он не предоставит достаточно доказательств.
Основатель закона — немецкий ученый Готфрид Вильгельм Лейбниц. В повседневной жизни часто встречается нарушение этого правила.
Подробнее о законах логики:
Формальная и математическая логика
Логика разделяется на 2 направления – формальное и математическое.
Формальная логика концентрируется на форме мышления, способах и методах перехода от предпосылок к правильным умозаключениям. Содержание мыслительного процесса ее не касается.
С точки зрения формальной логики, доказательство существования черных дыр ничем не отличается от обоснования необходимости взять с собой зонт в дорогу. Отцом-основателем этой ветви науки является древнегреческий мыслитель Аристотель.
Математическая логика занимается проблемой применения математических методов для решения логических задач и создания алгоритмов логического вывода.
В ней используется строгий символический язык, который позволяет уйти от проблемы нарушения закона тождества из-за ошибочного толкования отдельных терминов.
Поясним на примере:
| Символ математического языка | Значение |
|---|---|
| p | выражение «черепахи летают» |
| 0 | ложь |
| 1 | истина |
| ¬ | отрицание |
Вот так на языке математической логики можно описать выражение «черепахи могут летать»: |p|=0. А вот так выглядит фраза «черепахи не летают»: |¬p|=1.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Уметь мыслить логически — очень полезный навык, который сильно помогает в жизни. Жаль, что его почти не развивают в процессе обучения. Школьники и студенты просто зазубривают данные, не создавая логических связей между ними.
Значение логики сильно переоценивают. Многие гении часто принимали интуитивные и нелогичные решения, которые в последствии оказались судьбоносными. Не стоит возводить логику в культ.
Ну так черепахи летают или нет, что на сей счет думает математика? Я вот думаю, что летают, ведь если подбросить черепаху вверх, она будет лететь до тех пор пока не столкнется с Землей, а уберите силу тяжести и черепаха будет летать вечность.
Всё, что я понял из статьи, так только то, что никакого логического мышления у меня нет и никогда не было, вот так и живу, без логики.