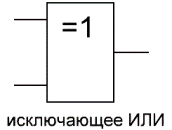логические элементы для чего нужны
Логические основы работы компьютера
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
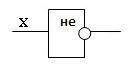
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
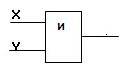
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
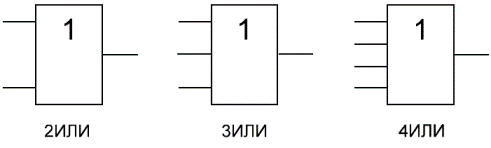
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
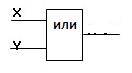
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.
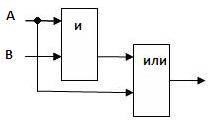
Составьте логическую схему для логического выражения: F=A \/ B /\ A.
1. Две переменные – А и В.
2. Две логические операции: 1-/\, 2-\/.
Пример 2.
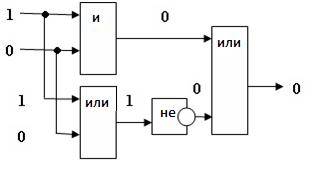
Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
4. Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0
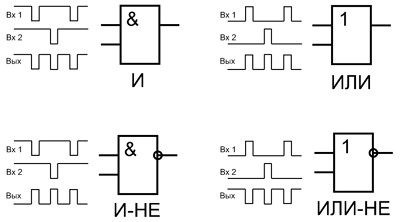
Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности
Электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными, называется логическим элементом. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня.
Операнды в данном случае подаются в двоичной системе счисления — на вход логического элемента поступают сигналы в форме напряжения высокого или низкого уровня, которые и служат по сути входными данными. Так, напряжение высокого уровня — это логическая единица 1 — обозначает истинное значение операнда, а напряжение низкого уровня 0 — значение ложное. 1 — ИСТИНА, 0 — ЛОЖЬ.
Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления. Для всех видов логических элементов, независимо от их физической природы, характерны дискретные значения входных и выходных сигналов.
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
В зависимости от устройства схемы элемента, от ее электрических параметров, логические уровни (высокие и низкие уровни напряжения) входа и выхода имеют одинаковые значения для высокого и низкого (истинного и ложного) состояний.
Традиционно логические элементы выпускаются в виде специальных радиодеталей — интегральных микросхем. Логические операции, такие как конъюнкция, дизъюнкция, отрицание и сложение по модулю (И, ИЛИ, НЕ, исключающее ИЛИ) — являются основными операциями, выполняемыми на логических элементах основных типов. Далее рассмотрим каждый из этих типов логических элементов более внимательно.
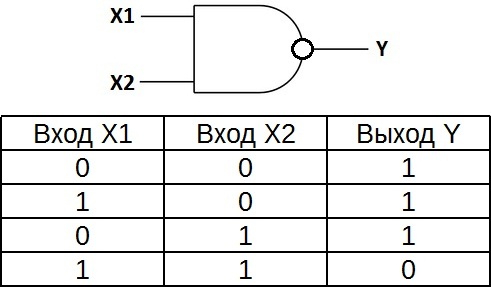
Таблица истинности для элемента 2И показывает, что на выходе элемента будет логическая единица лишь в том случае, если логические единицы будут одновременно на первом входе И на втором входе. В остальных трех возможных случаях на выходе будет ноль.
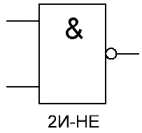
На западных схемах значок элемента «И» имеет прямую черту на входе и закругление на выходе. На отечественных схемах — прямоугольник с символом «&».
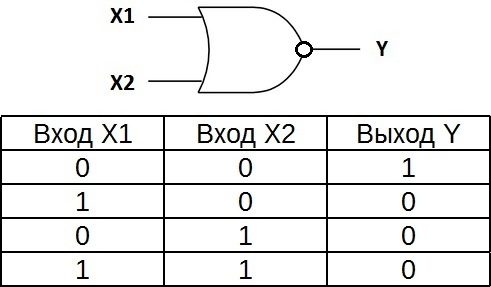
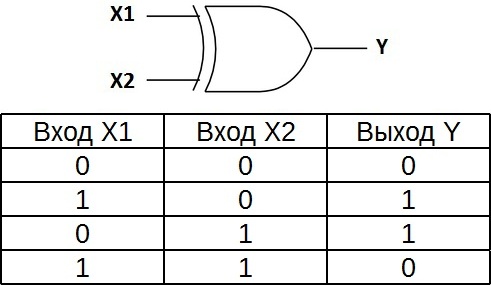
Таблица истинности для элемента «2ИЛИ» показывает, что для появления на выходе логической единицы, достаточно чтобы логическая единица была на первом входе ИЛИ на втором входе. Если логические единицы будут сразу на двух входах, на выходе также будет единица.
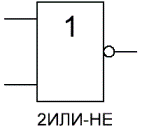
На западных схемах значок элемента «ИЛИ» имеет закругление на входе и закругление с заострением на выходе. На отечественных схемах — прямоугольник с символом «1».
Таблица истинности для инвертора показывает, что высокий потенциал на входе даёт низкий потенциал на выходе и наоборот.
На западных схемах значок элемента «НЕ» имеет форму треугольника с кружочком на выходе. На отечественных схемах — прямоугольник с символом «1», с кружком на выходе.
Таблица истинности для элемента «И-НЕ» противоположна таблице для элемента «И». Вместо трех нулей и единицы — три единицы и ноль. Элемент «И-НЕ» называют еще «элемент Шеффера» в честь математика Генри Мориса Шеффера, впервые отметившего значимость этой логической операции в 1913 году. Обозначается как «И», только с кружочком на выходе.
Изображение в западных схемах — как у «ИЛИ» с дополнительной изогнутой полоской на стороне входа, в отечественной — как «ИЛИ», только вместо «1» будет написано «=1».
Этот логический элемент еще называют «неравнозначность». Высокий уровень напряжения будет на выходе лишь тогда, когда сигналы на входе не равны (на одном единица, на другом ноль или на одном ноль, а на другом единица) если даже на входе будут одновременно две единицы, на выходе будет ноль — в этом отличие от «ИЛИ». Данные элементы логики широко применяются в сумматорах.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
8.3. Логические элементы
Все, абсолютно все электронные компоненты, обрабатывающие цифровые сигналы, состоят из небольшого набора одинаковых «кирпичиков». В микросхемах малой степени интеграции могут быть единицы и десятки таких элементов, а в современных процессорах их может быть очень и очень много. Они называются логические элементы. Логическим элементом называется электрическая схема, предназначенная для выполнения какой-либо логической операции с входными данными. Логический элемент — элемент, осуществляющий определенные логические зависимость между входными и выходными сигналами. Входные данные представляются здесь в виде напряжений различных уровней, и результат логической операции на выходе — также получается в виде напряжения определенного уровня. Логические элементы обычно используются для построения логических схем вычислительных машин, дискретных схем автоматического контроля и управления.
Тем не менее, принцип работы цифровой логики остается неизменным – на входе логического элемента (входов может быть несколько) должен быть цифровой сигнал (сигналы, если входов несколько), который однозначно определяет сигнал на выходе логического элемента.
Конечно, логические элементы строятся, в свою очередь, из уже рассмотренных в предыдущих уроках резисторов, транзисторов и других электронных компонентов, но с точки зрения разработки цифровых схем именно логический элемент является их «элементарной» частицей.
Еще несколько замечаний. Логические элементы (как, впрочем, и другие элементы электронных схем) принято обозначать так, чтобы входы были слева, а выходы справа. Число входов может быть, вообще говоря, любым, отличным от нуля. Реальные цифровые микросхемы могут иметь до 8 входов, но мы ограничимся двумя – этого достаточно для понимания. Условные обозначения соответствуют отечественному ГОСТу, в других стандартах они могут быть иными.
Какие же бывают логические элементы?
Логические элементы имеют один или несколько входов и один или два (обычно инверсных друг другу) выхода. Значения «нулей» и «единиц» выходных сигналов логических элементов определяются логической функцией, которую выполняет элемент, и значениями «нулей» и «единиц» входных сигналов, играющих роль независимых переменных. Существуют элементарные логические функции, из которых можно составить любую сложную логическую функцию.
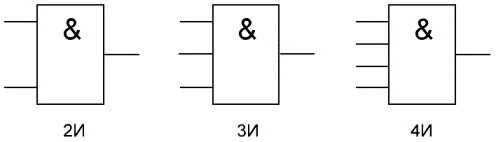
Элемент «И» (AND), он же конъюнктор, выполняет операцию логического умножения:
Здесь изображен логический элемент «2И» (цифра перед буквой «И» означает число входов). Знак & (амперсант) в левом верхнем углу прямоугольника указывает, что это логический элемент «И». Первые две буквы обозначения DD1.2 указывают на то, что это цифровая микросхема (Digital), цифра слева от точки указывает номер микросхемы на принципиальной схеме, а цифра справа от точки – номер логического элемента в составе данной микросхемы. Одна микросхема может содержать несколько логических элементов.
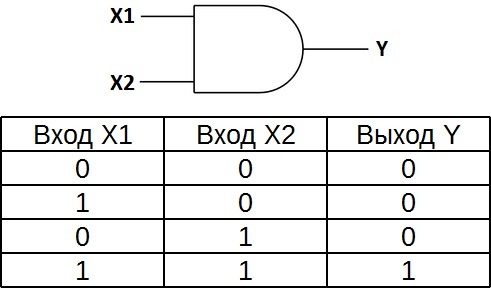
Состояние входов в таблице обозначаются «0» и «1» («ложь» и «истина»). Из таблицы видно, что выход «Y» будет иметь состояние «1» только в том случае, когда на обоих входах «Х1» и «Х2» будут «1». Это легко запомнить: умножение на «0» всегда дает «0».
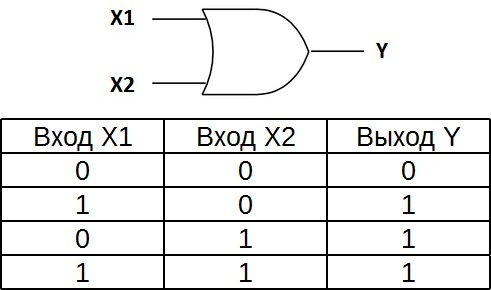
Элемент «ИЛИ» (OR), он же дизъюнктор, выполняет операцию логического сложения:
Состояние «1» на выходе будет всегда, пока есть хотя бы одна «1» на входах.
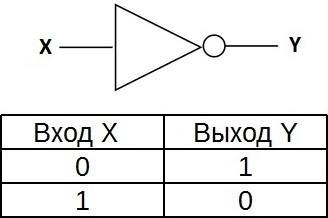
Элемент «НЕ» (NOT), он же инвертор, выполняет операцию логического отрицания:
Состояние на входе обратно состоянию на входе.
Вот из этих трех элементов строятся все цифровые устройства!
Рассмотрим еще три логических элемента, которые можно получить, комбинируя уже рассмотренные. В силу исторически сложившихся схемотехнических решений эти скомбинированные схемы тоже считаются логическими элементами.
Элемент «И-НЕ» (NAND), конъюнктор с отрицанием:
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» будет единица. И наоборот.
Элемент «ИЛИ-НЕ» (NOR), дизъюнктор с отрицанием:
Элемент работает так же как и «ИЛИ», но с инверсией выхода.
Элемент «Исключающее ИЛИ» (XOR), сумматор по модулю 2:
В этом элемента «1» на выходе будет только тогда, когда на входах разные состояния.
На таких элементах строят сумматоры двоичных многоразрядных чисел. Для этого используется еще один дополнительный выход, на котором при появлении на входах двух «1» появляется сигнал переноса разряда.
Мы рассмотрели логические элементы, которые применяются в цифровой технике для построения логических схем любого уровня сложности, но рассмотренные нами элементы не могут делать одну крайне важную работу – они не умеют хранить информацию. Для хранения используется более сложный класс устройств, называемый элементами с памятью или конечными автоматами. В этот класс входят триггеры, регистры, счетчики, шифраторы (дешифраторы), мультиплексоры (демультиплексоры) и сумматоры. Некоторый из этих устройств мы рассмотрим в следующем уроке.
ElectronicsBlog
Обучающие статьи по электронике
Логические элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ
Всем доброго времени суток! Продолжаю рассказывать про цифровые логические микросхемы. Здесь смотрите первую и вторую часть.
Рассказывая про логические микросхемы мы идём по пути повышения сложности логических элементов. После логических элементов НЕ и буферных микросхем следующие элементы, о которых идёт речь, выполняют простейшие логические операции: операция логического умножения и логического сложения. Такие элементы называются логические элементы И (AND) и логический элемент ИЛИ (OR). Данные логические элементы объединяет то, что они имеют несколько равноправных входов (от 2 до 12), а выход всего один. На выходе сигнал соответствует комбинации сигналов на входе, над которыми выполнена соответствующая функция. Ниже показано условное графическое обозначение элементов И и ИЛИ.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
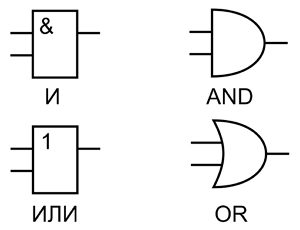
Обозначение элементов И и ИЛИ: слева логический элемент И и ИЛИ (DIN); справа логический элемент И и ИЛИ (ANSI).
Кроме многочисленных логических элементов И и ИЛИ существуют такие логические элементы, которые на выходе инвертируют сигнал. К названию таких элементов добавляется в конце частичка НЕ, то есть элемент И с инверсией сигнала на выходе называется И-НЕ (NAND), а элемент ИЛИ соответственно ИЛИ-НЕ (NOR). Ниже показано условное графическое обозначение элементов И-НЕ и ИЛИ-НЕ.
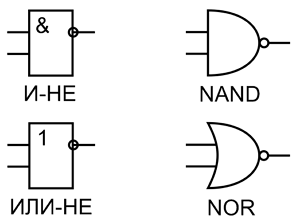
Обозначение элементов И-НЕ и ИЛИ-НЕ: слева логический элемент И-НЕ и ИЛИ-НЕ (DIN); справа логический элемент И-НЕ и ИЛИ-НЕ (ANSI).
Как указывалось выше, данные элементы имеют несколько равноправных входов, поэтому для чёткого распознавания логических элементов с разным количеством входов перед названием логического элемента ставят число, которое соответствует количеству входов логического элемента. Например, обозначение двухвходового элемента И с инверсией на выходе будет иметь обозначение 2И-НЕ, а пятивходового элемента выполняющего функцию ИЛИ с инверсией – 5ИЛИ-НЕ.
Отечественная система обозначений чётко определяет наименования микросхем, выполняющих различные функции. Такие обозначения различаются суффиксами: для логических элементов выполняющих функцию И наименование содержит суффикс ЛИ (например, К155ЛИ2, КР1533ЛИ10), для элементов И-НЕ – суффикс ЛА (например, К155ЛА3, К555ЛА13), для элементов ИЛИ – суффикс ЛЛ (например, К155ЛЛ1, К1533ЛЛ4), для элементов ИЛИ-НЕ – суффикс ЛЕ (например, К155ЛЕ1, К1533ЛЕ10).
Как известно для каждого логического элемента выполняющего соответственную функцию существует своя таблица истинности. Ниже приведена сводная таблица истинности для двухвходовых логических элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ.
| Сигналы на входе | Сигналы на выходе | ||||
| 1 | 2 | И | И-НЕ | ИЛИ | ИЛИ-НЕ |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
Применение логоческих элементов
На современном этапе развития цифровой электроники и микросхемотехники простые логические элементы всё меньше находят своё применение именно как выполняющие простые логические функции. Очень часто вышеописанные логические элементы выполняют функции разрешения/запрещения или смешивания/совпадения сигналов в более сложных цифровых схемах.
Схема разрешения/запрещения
Например, применение логического элемента 2И в качестве управляющего можно описать следующим образом. Один из входов считают управляющим, а второй информационным, тогда при лог. 1 на управляющем входе, сигнал с информационного входа проходит на выход без ограничения, но если на управляющем входе низкий логический уровень, то прохождение сигнала с входа на выход отсутствует. Очень часто логические элементы в таком качестве используют для работы на мультиплексированную или двунаправленную линию.
Точно также в качестве элементов разрешении/запрещения используются и другие элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ. Применение того или иного элемента обуславливается уровнем управляющего сигнала, инверсии (или её отсутствия) входного сигнала. Ниже показаны схемы использования логических элементов в качестве разрешающих/запрещающих прохождение сигнала.
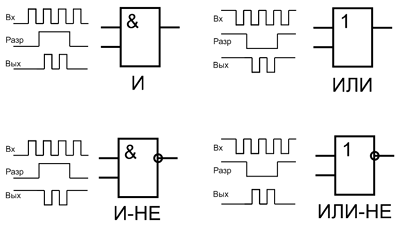
Реализация разрешение/запрещение прохождения сигналов на логических элементах
Схема смешивания сигналов
Довольно часто требуется реализовать смешивание сигналов, когда выходной сигнал должен появляться при приходе сигналов на любой вход логического элемента. Например, использую элемент 2ИЛИ можно реализовать смешивание двух сигналов без инверсии, то есть сигналы, которые приходят на первый и на второй вход, будут отображаться в выходном сигнале. Ниже показаны схемы использования логических элементов в качестве смешивающих с различными уровнями.
Реализация смешивания сигналов различных логических уровней на логических элементах
Схемы определения совпадения сигналов
На логических элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ очень просто реализовать схемы совпадения входящих сигналов, когда выходной сигнал вырабатывается при совпадении логических уровней входящих сигналов. Ниже показаны схемы совпадения на логических элементах.
Реализация функции совпадения сигналов на логических элементах
Схемы инвертирования сигналов
Логические элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ, как более сложные по сравнению с элементами НЕ и повторителями, позволяют реализовать функции инверторов и буферных элементов. Для этого просто необходимо соединить их входы или на один из входов подать сигнал соответствующего логического уровня. Ниже показаны схемы повторителей и инверторов на элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.

Реализация повторителей и инверторов на логических элементах
Этими простыми схемами не ограничивается применение логических элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ. Больше про применение логических микросхем я обязательно напишу в одном из следующих постов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Логические элементы – определение, свойства
Специальные устройства, выполняющие обработку цифровой информации на основе принципов алгебры логики, называются логическими элементами. Физически они реализовываются на электронных устройствах. Самыми простыми логическими элементами являются И, ИЛИ, НЕ.
Что такое логические элементы
Логические элементы представляют собой устройства, которые могут быть реализованы на электронной полупроводниковой базе. Они выполняют некоторую логическую функцию преобразования входного сигнала. На нескольких простых логических элементах можно построить сколь угодно много сложных устройств, например регистров, сумматоров, счетчиков импульсов.
Для описания работы различных электронных устройств удобно использовать элементы алгебры логики, которая, как известно, работает с переменными, принимающими только два значения 1 и 0, то есть включено или выключено.
Определение количества логических элементов, которые можно построить на базе двоичной логики, выполняется по формуле 24, то есть составляет 16.
Элементарные логические элементы
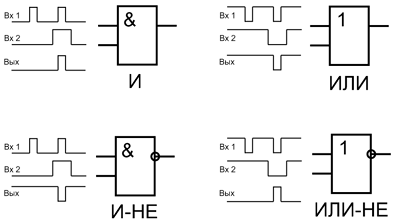
Основными логическими элементами являются И, ИЛИ, НЕ. Все остальные элементы строятся на базе них.
Рис. 1. Графическое изображение элементов И, ИЛИ, НЕ
Инверсия (НЕ)
Инверсия представляет собой унарную операцию, то есть элемент с одним входом. Логический элемент НЕ реализует логическое отрицание. Если на вход этого элемента подается сигнал 1, то на выходе будет получено 0.
Таблица истинности для данного элемента имеет вид:
Конъюнкция (И)
Логический элемент И является бинарным и выполняет логическое умножение. Результат конъюнкции равен 1 только в том случае, когда на входы данного элемента подаются две единицы. Во всех остальных случаях результат конъюнкции равен нулю.
Таблица истинности для конъюнкции
Дизъюнкция (ИЛИ)
Бинарный логический элемент ИЛИ реализует операцию логического сложения. Результат этой операции равен нулю в том случае, когда на входы дизъюнкции подаются нули. В остальных случаях результат всегда равен единице.
Таблица истинности для логического ИЛИ
Логические элементы, построенные на базе И, ИЛИ, НЕ
Все остальные бинарные логические элементы строятся на базе основных.
Например, если к элементу И добавить инверсию, то получится новый логический элемент И-НЕ, который также называется Штрих Шеффера. Обозначается знаком «|» – вертикальная черта. Результатом этой функции будет ноль, только в том случае, когда на вход подаются две единицы.
Инверсия дизъюнкции позволит получить элемент ИЛИ_НЕ, носящий также название стрелка Пирса. При записи обозначают стрелкой, направленной вниз «↓». В результате этой функции на выходе будет единица только при нулевых входных сигналах, а все остальные случаи нулевые.
Рис. 2. Графическое изображение элементов И-НЕ, ИЛИ-НЕ
Все логические элементы собираются из различных устройств: транзисторов, резисторов, диодов, интегральных микросхем. Самыми распространенными являются электронные логические элементы, так как показывают хорошие свойства быстродействия, надежности, экономичности.
Рис. 3. Принципиальная схема логического элемента
Что мы узнали?
Логические элементы – это устройства, собранные из различных электронных приборов и выполняющие функцию преобразования сигнала на основе алгебры логики. Самыми элементарными логическими элементами являются И, ИЛИ, НЕ. Все остальные строятся на основе базовых.