лемма и теорема в чем отличие
Понятие Теорема и Аксиома Лемма, Следствия с тестами кратко
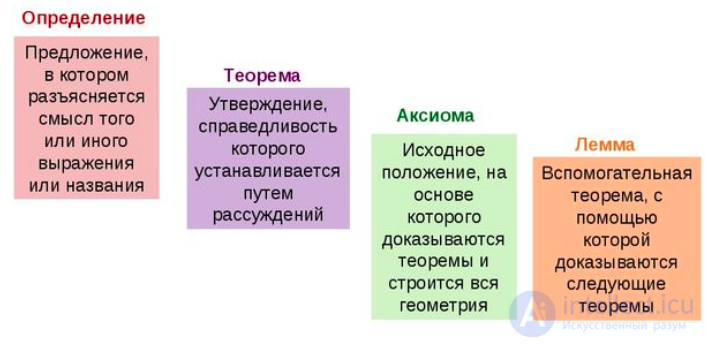
В математических дисциплинах широко используются четкие понятия такие как определения, теоремы, леммы, аксиомы, расссмотрим что это такое?
теорема (др.-греч. θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод). В отличие от теорем, аксиома ми называются утверждения, которые в рамках конкретной теории принимаются истинными без всяких доказательств или обоснований.
В математических текстах теоремами обычно называют только те доказанные утверждения, которые находят широкое применение в решении математических задач. При этом требуемые доказательства обычно кем-либо найдены (исключение составляют в основном работы по логике, в которых изучается само понятие доказательства, а потому в некоторых случаях теоремами называют даже неопределенные утверждения). Менее важные утверждения-теоремы обычно называют лемма ми,предложениями, следствия ми, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называютгипотезами.
Наиболее знаменитыми являются теоремы Ферма, Пифагора и Птолемея.
Лемма (греч. λημμα — предположение) — доказанное утверждение, полезное не само по себе, а для доказательства других утверждений. Примеры известных лемм —лемма Евклида, лемма Жордана, лемма Гаусса, лемма Накаямы, лемма Гриндлингера, Лемма Лоренца, Лемма Лебедева.
Аксиома (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое в основе доказательства других ее положений.
Необходимость в принятии аксиом без доказательств следует из индуктивного соображения: любое доказательство вынуждено опираться на какие-либо утверждения, и если для каждого из них требовать своих доказательств, цепочка получится бесконечной. Чтобы не уходить в бесконечность, нужно где-то эту цепочку разорвать — то есть какие-то утверждения принять без доказательств, как исходные. Именно такие, принятые в качестве исходных, утверждения и называются аксиомами.
В современной науке аксиомы — это те положения теории, которые принимаются за исходные, причем вопрос об истинности решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.
Набор аксиом называется непротиворечивым, если из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание. Аксиомы являются своего рода «точками отсчета» для построения теорий в любой науке, при этом сами они не доказываются, а выводятся непосредственно из эмпирического наблюдения (опыта) или обосновываются в более глубокой теории.
Австрийский математик Курт Гедель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система) начиная с определенного уровня сложности либо внутренне противоречива, либо неполна (то есть в достаточно сложных системах найдется хотя бы одно высказывание, истинность и ложность которого не может быть доказана средствами самой этой системы ).
Следствие — утверждение, которое выводится непосредственно из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Приведем примеры следствий из аксиомы о параллельности прямых:
История
Впервые термин «аксиома» встречается у Аристотеля (384—322 до н. э.) и перешел в математику от философов Древней Греции. Евклид различает понятия «постулат» и «аксиома», не объясняя их различия. Со времен Боэция постулаты переводят как требования (petitio), аксиомы — как общие понятия. Первоначально слово «аксиома» имело значение «истина, очевидная сама по себе». В разных манускриптах Начал Евклида разбиение утверждений на аксиомы и постулаты различно, не совпадает их порядок. Вероятно переписчики придерживались разных воззрений на различие этих понятий.
Отношение к аксиомам как к неким неизменным самоочевидным истинам сохранялось долгое время. Например, в словаре Даля аксиома — это «очевидность, ясная по себе и бесспорная истина, не требующая доказательств».
Сейчас аксиомы обосновываются не сами по себе, а в качестве необходимых базовых элементов теории. Критерии формирования набора аксиом в рамках конкретной теории часто являются прагматическими: краткость формулировки, удобство манипулирования, минимизация числа исходных понятий и т. п. Такой подход не гарантирует истинность принятых аксиом. Лишь подтверждение теории является одновременно и подтверждением набора ее аксиом.
Подведем итог и сделам сравнения и выявим сходства и различия
Тесты для самопроверки
1. Правило, которое принимается без доказательств.
2. Утверждение доказано с помощью аксиом, постулатов или других теорем, которые заведомо верны это
4.Математическое утверждение, которое НЕ требует доказательства, является
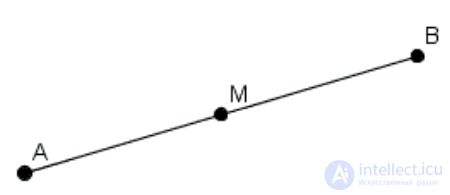
5.Если AB = 10, какое определение объясняет, почему AM = 5?
6. доказанное утверждение испольуемое для доказательства других утверждений
См. также
Статью про теорема я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое теорема,аксиома,лемма,следствия,аксиоматизация теории и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории введение в математику. основы
Лемма и теорема в чем отличие
Чем теорема отличается от аксиомы? И мне вопросик теорема вопросик аксиома
Теоре́ма (др.-греч. θεώρημα — «зрелище, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство (иначе говоря, вывод). В отличие от теорем, аксиомами называются утверждения, которые в рамках конкретной теории принимаются истинными без всяких доказательств или обоснований.
В математических текстах теоремами обычно называют только достаточно важные утверждения. При этом требуемые доказательства обычно кем-либо найдены (исключение составляют в основном работы по логике, в которых изучается само понятие доказательства, а потому в некоторых случаях теоремами называют даже неопределённые утверждения). Менее важные утверждения-теоремы обычно называют леммами, предложениями, следствиями, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называют гипотезами.
Аксио́ма (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, не доказываемое в рамках данной теории и лежащее в основе доказательства других ее положений.[1] В современной науке аксиомы — это те положения теории, которые принимаются за исходные, причём вопрос об истинности решается либо в рамках других научных теорий, либо посредством интерпретации данной теории.[1] Аксиоматиза́ция теории — явное указание конечного или счётного, рекурсивно перечислимого (как, например, в аксиоматике Пеано) набора аксиом и правил вывода. После того как даны названия изучаемым объектам и их основным отношениям, а также аксиомы, которым эти отношения должны подчиняться, всё дальнейшее изложение должно основываться исключительно лишь на этих аксиомах, не опираясь на обычное конкретное значение этих объектов и их отношений. Утверждения на основе аксиом называются теоремами. С формальной точки зрения, сами аксиомы также входят в число теорем. Примеры различных, но равносильных наборов аксиом можно встретить в математической логике и Евклидовой геометрии. Набор аксиом называется непротиворечивым, если из аксиом набора, пользуясь правилами логики, нельзя прийти к противоречию, то есть доказать одновременно и некое утверждение, и его отрицание. Аксиомы являются своего рода «точками отсчёта» для построения теорий в любой науке, при этом сами они не доказываются, а выводятся непосредственно из эмпирического наблюдения (опыта) или обосновываются в более глубокой теории. Австрийский математик Курт Гёдель доказал «теоремы о неполноте», согласно которым всякая система математических аксиом (формальная система) начиная с определённого уровня сложности либо внутренне противоречива, либо неполна (то есть в достаточно сложных системах найдётся хотя бы одно высказывание, истинность и ложность которого не может быть доказана средствами самой этой системы).[2]
Прочитайте и сами сделайте вывод
Юлия Сергеевна, я точно не помню. Там чего-то без доказательств, а к чему-то доказательство нужно. Или там где-то что-то однозначно, а что-то под сомнение ставится.
Если коротко,то. Теорема-утверждение,для которого требуется доказательство.Оксиома-не требует доказательства.
Аксиома принимается без доказательств, а теорему устанешь доказывать
Аксиома, в отличие то теоремы, не требует доказательств
Что такое аксиома, теорема, следствие
В данной публикации мы рассмотрим, что из себя представляют аксиомы, теоремы и следствия. Определения сопровождаются соответствующими примерами для лучшего понимания.
Что такое аксиома
Для того, чтобы решить многие математические задачи, очень часто требуется выполнить определенные логические действия, благодаря которым удается получить то или иное решение/доказательство.
Но есть в математике такие утверждения, которые не требуют никаких доказательств.
Например:
Эти и другие подобные утверждения, не нуждающиеся в доказательстве и принимаемые в качестве исходных в какой-либо теории, называются аксиомами (от древнегреческого “axioma”, что означает “положение”, “утверждение”). Иногда их еще называются постулатами.
Аксиомы могут использоваться для решения конкретных задач или применяться для доказательства теорем.
Примечание: не допускается искажение формулировок аксиом и большинства теорем, т.е. их нужно учить наизусть.
Что такое теорема
В отличие от аксиомы, теорема – это суждение, которе требуется доказать. Т.е. в рассматриваемой теории для нее есть определенное доказательство.
Например:
Есть отдельный вид так называемых вспомогательных теорем, которые сами по себе не полезны и используются только для доказательства других теорем. Их называются леммами (от древнегреческого “lemma”, что означает “предположение”).
Например:
Если произведение нескольких сомножителей делится на простое число p, то по крайней мере один из сомножителей делится на p (лемма Евклида).
Что такое следствие
Следствие – это утверждение, которое было выведено из аксиомы или теоремы. И оно, также, требуется доказательства.
Например:
ЛЕММА
Полезное
Смотреть что такое «ЛЕММА» в других словарях:
ЛЕММА — (греч. lemma, от lambano думаю, убеждаю). Предложение, доказанное раньше, на котором основывается последующее. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЛЕММА в логике и математике положение, доказанное… … Словарь иностранных слов русского языка
лемма — теорема Словарь русских синонимов. лемма сущ., кол во синонимов: 1 • теорема (5) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ЛЕММА — (от греческого lemma допущение), теорема, не имеющая самостоятельного значения, но используемая для доказательства других теорем … Современная энциклопедия
ЛЕММА — вспомогательное предложение, употребляемое при доказательстве одной или нескольких теорем … Большой Энциклопедический словарь
ЛЕММА — ЛЕММА, леммы, жен. (греч. lemma) (мат.). Теорема, не имеющая самостоятельного значения, нужная лишь для доказательства другой теоремы. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЛЕММА — ЛЕММА, ы, жен. В математике: вспомогательная теорема, необходимая для доказательства другой теоремы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ЛЕММА — жен., греч. математическое предложенье, выводимое следствием из предыдущего, доказанного. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
лемма
Смотреть что такое «лемма» в других словарях:
ЛЕММА — (греч. lemma, от lambano думаю, убеждаю). Предложение, доказанное раньше, на котором основывается последующее. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЛЕММА в логике и математике положение, доказанное… … Словарь иностранных слов русского языка
ЛЕММА — (от греч. lemma) – предложение, положение; в математике – вспомогательное предложение, употребляемое при доказательстве одной или нескольких теорем. Философский энциклопедический словарь. 2010. ЛЕММА … Философская энциклопедия
лемма — теорема Словарь русских синонимов. лемма сущ., кол во синонимов: 1 • теорема (5) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ЛЕММА — (от греческого lemma допущение), теорема, не имеющая самостоятельного значения, но используемая для доказательства других теорем … Современная энциклопедия
ЛЕММА — вспомогательное предложение, употребляемое при доказательстве одной или нескольких теорем … Большой Энциклопедический словарь
ЛЕММА — ЛЕММА, леммы, жен. (греч. lemma) (мат.). Теорема, не имеющая самостоятельного значения, нужная лишь для доказательства другой теоремы. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЛЕММА — ЛЕММА, ы, жен. В математике: вспомогательная теорема, необходимая для доказательства другой теоремы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ЛЕММА — жен., греч. математическое предложенье, выводимое следствием из предыдущего, доказанного. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля