кто доказал что параллельные прямые не пересекаются
Такое ощущение, что автор живёт на плоскости, раз «Начала» Евклида «прекрасно описывают пространство, в котором мы живем».
отличная статья, получил эстетическо-математическое удовольствие, спасибо!
В Чечне учения местных сил обороны, без флагов РФ
Нет работы.
Сегодня ехал в троллейбусе и подслушал разговор. Трудно было не подслушать, перешли уже на повышенные.
Кондуктор же парировала, что эти пять тысяч можно заработать всегда, неважно, есть документы или нет.
Ой, что тут началось. и на «приведите пример, возьмут ли его куда-то кондуктором?», я вмешался. Мне сейчас нужен упаковщик. Вот прям срочно! На тестовую партию. нужно упаковать три тысячи отправлений. А у меня нет такой штатной единицы. Просто взять из большой коробки и переложить в маленькие. Я предложил её супругу 20 000 за десять дней за такую работу. Женщина обрадовалась и согласилась.
Должна была сегодня позвонить)))
Как вы поняли, сижу пакую)))
С днём рождения Юра!
Мигранты
Идеальное название
Прометей дарит огонь людям
Мать солдата
В Орле арестовали человека национальности, которую нельзя называть
В Орле арестовали человека неопределённой национальности, за то, что тот силой затащил в машину 14-летнюю русскую девочку и надругался над ней.
Девочка чудом смогла убежать и сообщить обо всем родителям.
О национальности насильника не известно, кроме того что его зовут Аслаханов Ислам и он уроженец Чечни.
Может русский, может украинец, или норвежец. Тут сложно понять, нужен антрополог.
Возбуждено уголовное дело по ч. 3 ст. 132 УК РФ. Лицо неустановленной национальности помещено в СИЗО.
Избивавший русского срочника в армии, боец ММА избежал наказания
Избивавший срочника в армии, боец ММА избежал наказания. Сейчас он с компанией гоняет по улицам со скоростью 200 км в час
Новое в блогах
Пересекаются ли параллельные или Что говорил Лобачевский?
Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.
Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.
Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.
Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:
«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.
При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!
Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!
Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.
Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.
Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.
Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!
Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.
Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.
Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»
«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»
Геометрия Лобачевского
Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.
Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.
И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.
Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.
Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.
Аксиома параллельности Лобачевского выглядит следующим образом:
Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.
Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.
Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.
Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.
В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».
Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».
Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:
В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.
Кто доказал что параллельные прямые не пересекаются
Знаете, как сложно иметь небольшое представление об элементарной математике? Листаешь ленту, как вдруг видишь, что кто-то обсуждает пятый постулат Евклида и геометрию Лобачевского. Пытаешься людей образумить, а они оказываются дилетантами, начинают тебе тыкать, что, мол, Лобачевский доказал, что параллельные прямые пересекаются. И В ЭТОТ МОМЕНТ НАЧИНАЕТ ДИКО ГОРЕТЬ, ВЕДЬ ТВОЙ СОБЕСЕДНИК СЧИТАЕТ ТУПЫМ ТЕБЯ, ТАК КАК ТЫ НИЧЕГО НЕ ЗНАЕШЬ О НЕЕВКЛИДОВОМ МИРЕ. Так вот, эта статья – это жест отчаяния и надежды, это попытка привнести чего-то своего в просвещение.
Началось всё очень давно, еще когда у римлян только планировались Пунические войны, а до нашествия гуннов было больше 500 лет. Евклид задавался вопросами геометрии и создал фундаментальный труд – «Начала». Там был пятый постулат, который гласил, что через точку, не лежащую на прямой, можно провести лишь одну прямую, параллельную данной (оригинальная формулировка другая, но ее хер кто поймет с первого раза, а она тут не главная). И да простят меня незнающие, ЭТО НЕ ТО ЖЕ САМОЕ, ЧТО ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ НЕ ПЕРЕСЕКАЮТСЯ, ВЕДЬ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ НЕ ПЕРЕСЕКАЮТСЯ, ПОТОМУ ЧТО ОНИ ОПРЕДЕЛЯЮТСЯ, КАК НЕПЕРЕСЕКАЮЩИЕСЯ.
Ну так вот, этот пятый постулат пытались доказать через 4 общепринятых аксиомы многие чуваки, но у них ничего не получалось. Тогда несколько умных чуваков решили, что лучше использовать метод от противного (о любовном треугольнике Бойяи-Гаусс-Лобачевский также нужна отдельная статья, там такие страсти кипели). Так появилась первая неевклидова геометрия, которая известна, как геометрия Лобачевского или гиперболическая (что тоже не совсем верно). Затем появились и другие интересные штуки, о некоторых из них в кратце расскажу.
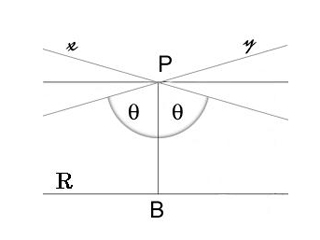
1) Геометрия Лобачевского. Если кратко – посылаем к черту пятый постулат, а именно, говорим, что через точку, не лежащую на прямой, можно провести по крайней мере две прямых, параллельных данной и мутим свою геометрию. Например, если мы возьмём асимптотическую прямую к другой прямой и проведём перпендикуляр «a» ко второй прямой, то, зная перпендикуляр «а», мы захотим найти угол α, то нам нужно будет использовать функцию α=π(а) (но более подробно об этом в будущем). Лобачевский вывел кучу крутых штук, чтобы описать свою геометрию, только вот было неясно, где это все реализовать. Сам математик умер, не получив признания, так что додумывать, на чем рисовать пришлось другим математикам, и вот появилось поверхность – псевдосфера, но только на ней геометрия Лобачевского выполняется только в некоторых случаях, так что это не особо удобно. Затем появилась модель Римана и Пуанкаре, которые удобнее.
2) Геометрия Римана на сфере. Риман, в отличие Лобачевского, вообще не парился и сказал, а давайте вообще параллельных прямых не будет, прям вообще, и замутил геометрию, в которой прямыми будут окружности на сфере. То есть мы находим проекцию построенного треугольника и вычисляем там углы, синусы, косинусы и т.д.
3) Проективная геометрия – это вообще самая интересная вещь. Если сказать, что прямые и точки на самом деле это почти одно и то же, а еще, что параллельные прямые перескаются, просто бесконечно далеко, то всё обретает смысл. И правда, когда вы смотрите на рельсы, вы видите, что они параллельны. Когда посмотрите на горизонт, увидите, что они где-то пересеклись. Пойдете в ту сторону и никогда не придете к месту их пересечения. Значит, они пересекаются бесконечно далеко. Эта идея обыгрывается в проективной геометрии (но для нее также нужна отдельная статья). Одна из моделей проективной плоскости позволяет представить ее, как круг, в котором точки, лежащие на противоположных концах одного диаметра, отождествлены. Если окружность склеить так, чтобы отождествленные точки стали одной точкой, получится компактное двумерное многообразие, правда без самопересечений оно не вкладывается в наш локально-евклидов трехмерный мирок.
Заключение: неевклидовы геометрии – это крутая и нужная вещь (спросите физиков и астрономов или прогеров).
Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite
Геометрия Лобачевского
Дата публикации: 20.12.2016 2016-12-20
Статья просмотрена: 2019 раз
Библиографическое описание:
Бокова, К. Д. Геометрия Лобачевского / К. Д. Бокова, И. Г. Майоров, Д. В. Козлова, Н. Ю. Потапова. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 13-15. — URL: https://moluch.ru/young/archive/9/626/ (дата обращения: 25.11.2021).
1. Постановка проблемы
Все мы в школе проходим курс геометрии — науки, в которой кто-то не видит смысла, а иные находят свое призвание. При этом мы изучаем Евклидову геометрию, зародившуюся более двух тысяч лет назад, но и сейчас остающуюся актуальной. Но почти все слышали и о других, так называемых неевклидовых геометриях, в частности — о геометрии Лобачевского. И самое странное, что знакомство с этой наукой заканчивалось на утверждении, что она допускает возможность пересечения параллельных прямых. Этот факт удивляет, даже поражает, но, как и все непонятное, воспринимается на веру.
А ведь на самом деле геометрия Лобачевского не так уж сильно отличается от привычной нам геометрии и тот факт, что параллельные прямые в ней пересекаются — это досужий миф, родившийся при странных обстоятельствах. Но, для того чтобы это понять, необходимо хотя бы вкратце разобрать историю появления геометрии как науки.
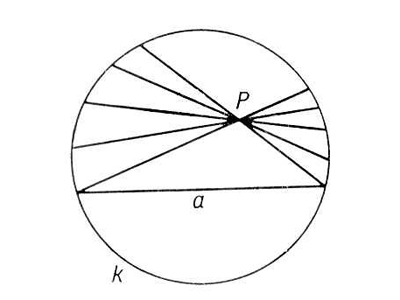
Пятый постулат геометрии Лобачевского утверждает, что если на плоскости лежат прямая иточка, то через эту точку можно провести хотя бы две прямые, не пересекающиеся спервой прямой.
Рис.1 Иллюстрация пятого постулата
А в геометрии Евклида через точку А можно провести только одну-единственную прямую. Таким образом, неевклидова геометрия допускает, что на одной плоскости может находиться сразу несколько прямых линий, не пересекающихся друг с другом.
А утверждение о возможности пересечения параллельных прямых в геометрии Лобачевского возникло из-за простого незнания аксиом этой геометрии. Ведь при ближайшем рассмотрении оказывается, что в неевклидовой геометрии не только не говорится о пересечении параллельных прямых, но и не говорится о параллельных прямых вообще — разговор здесь идет именно о непересекающихсяпрямых, находящихся на одной плоскости.
2. Лобачевский Николай Иванович
Рис.2. Лобачевский Н. И.
Лобачевский и не подозревал о своём могучем таланте математика. Будучи студентом первого курса Казанского университета, он изучал медицину. Деятельность Лобачевского неразрывно связана с историей Казанского университета, который был открыт в 1805 году. В 1827 году Николай Иванович становится ректором Казанского университета, находится он в этой должности непрерывно в течение 19 лет.
Деятельность Лобачевского вызывает изумление. Наряду с большой административной и педагогической работой он, не покладая рук, занимался и наукой. Ему было всего 34 года, когда он решил «многовековую» проблему V постулата из «Начал» Евклида и построил свою, неевклидову геометрию.
Имя Лобачевского известно всему миру. Он вошёл в историю математики как революционер в науке и «Коперник геометрии». Он решил проблему, над которой человечество бесплодно билось более двух тысяч лет. Анализируя попытки доказать V постулат, Лобачевский сделал чрезвычайно смелый вывод о его недоказуемости.
Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких аксиом (постулатов). Считалось, что эти аксиомы «очевидны», т. е. отражают свойства реального (физического) пространства.
Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова: «Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну прямую можно провести, является не аксиомой, а теоремой.
При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая — одна.
То есть, распространенное утверждение «Лобачевский доказал, что параллельные прямые могут и пересекаться» — является в корне неверным. Ведь это бы противоречило их определению.
Евклидова геометрия
Параллельнымипрямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. (В некоторых определениях совпадающие прямые не считаются параллельными). В свою очередь, существование непересекающихся в плоскости прямых является фактом абсолютной геометрии, т. е. фактом, который может быть доказан и без использования аксиомы Евклида, и без использования аксиомы Лобачевского. А именно, верно следующее утверждение: Если две прямые (в плоскости) перпендикулярны третьей, то они не пересекаются. В планиметрии Евклида любые непересекающиеся прямые — параллельны, в планиметрии Лобачевского это не так.
Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство лишь евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две).
Аксиомы Евклида
1. Аксиома принадлежности. Через любые две точки на плоскости можно провести прямую и притом только одну.
2. Аксиома порядка. Среди любых трёх точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.
3. Аксиома конгруэнтности (равенства) отрезков и углов. Если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой.
4. Аксиома непрерывности (аксиома Архимеда). Для любых двух отрезков AB и CD существует конечный набор точек A1, A2,…, An, лежащих на прямой AB, таких, что отрезки AA1, A1A2,…, An — 1An конгруэнтны (сравнимы) отрезку CD, a точка B лежит между A и An.
5. Аксиома параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
Среди пяти аксиом Евклида пятая резко выделяется своей неочевидностью. Она больше похожа на теорему: через точку, не лежащую на данной прямой, проходит ровно одна прямая, параллельная данной.
Многие учёные пытались вывести пятую аксиому из первых четырех. Среди них древнегреческие математики Птолемей и Прокл, иранский математик Омар Хайям, немецкие математики Клавиус и Ламберт, английский математик Валлис и многие другие.
Возникла мысль, что можно построить геометрию, где через точку, не лежащую на прямой, проходят по крайней мере две прямые, ей параллельные. 23 февраля 1826 года на заседании математического факультета Казанского университета российский математик Николай Иванович Лобачевский заявил, что пятый постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную и свободную от противоречий, как и евклидова.
Одновременно к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше.
Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций. В итоге Н.Лобачевский выступил как первый наиболее яркий и последовательный пропагандист новой геометрии.
Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он выбрал метод «от противного», т. е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится. (Т. е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование.)
Конечно, в первое время его выкладки не признавали. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что, основываясь на логике, теория Лобачевского ничем не хуже евклидовой.
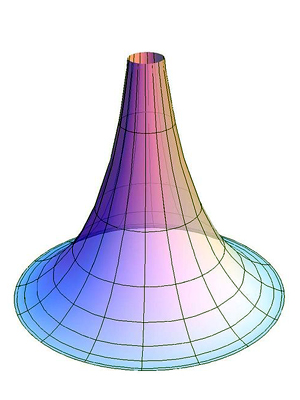
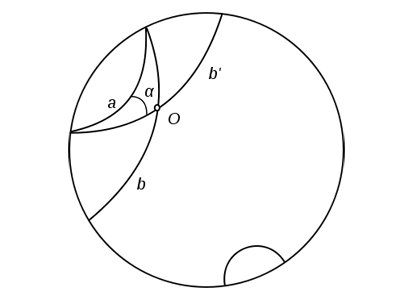
Один из простых, но хитрых способов убедиться в этом — придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один. Пожалуй, самой простой является модель Пуанкаре. Её возможно построить самим, при чем довольно легким способом.
Рис. 3. Модель Пуанкаре
Для того всего лишь потребуется: начертить на листке бумаги прямую. Взять циркуль и, ставя его иглу на эту прямую, нарисовать полуокружности, находящиеся с одной стороны от прямой. Затем стереть прямую (и с ней — концевые точки полуокружностей). Эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского.
Выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли), т. е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их — бесконечное множество.
За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий (Инверсия представляет собой более сложное преобразование геометрических фигур, при котором прямые уже могут переходить в окружности) относительно окружностей, дуги которых служат прямыми. В геометрии Лобачевского прямые на плоскости либо пересекаются, либо параллельны, либо являются расходящимися.
Рис. 4. Прямые в геометрии Лобачевского
В геометрии Лобачевского сохраняются все теоремы, которые можно доказать без использования аксиомы параллельности. В геометрии Лобачевского нет подобных треугольников. В геометрии Лобачевского имеет место четвертый признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.
Все! Перечеркнуты «Начала». Довольно мысль на них скучала.
Хоть прав почти во всем Евклид, но быть не вечно постоянству.
И плоскость свернута в пространство, и мир иной имеет вид.
Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.
Петербургский ученый А. А. Фридман в 1922 обнаружил, что Вселенная расширяется и является пространством Лобачевского. Отклонения геометрии Лобачевского от евклидовой геометрии растут с увеличением размеров. Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства, ибо в пределах солнечной системы, и даже нашей галактики, эти размеры так малы, что погрешность измерений не позволяет их обнаружить. Вот почему, живя в пространстве Лобачевского, мы пользуемся геометрией Евклида!
За год до смерти, будучи совершенно слепым, Лобачевский диктует своим ученикам новое сочинение, названное им «Пангеометрией», где показывает, что евклидова геометрия есть частный случай неевклидовой геометрии. Эту последнюю свою работу он с любовью посвящает Казанскому университету, где прошла вся его творческая жизнь.
Заключение
Таким образом, мы представили вам одну из самых на первый взгляд невероятных и противоречивых теорем. Теорема Лобачевского в начале кажется сложной и непонятной, но вызывает огромный интерес (по крайней мере, таковой она вызвала у нас). А все, что вызывает интерес должно быть изучено, что мы и сделали. При подробном её рассмотрении теорема оказывается вполне логичной, и потому простой для восприятия.
Гений Лобачевского в том, что он смог выйти за поставленные многовековыми устоями границы, смог доказать то, что практически все наши знания весьма и весьма относительны. И все может быть устроено вовсе не так, как мы привыкли это воспринимать. Его смелая идея помогает расширить кругозор, помогает по-иному взглянуть на привычный нам мир. И потому эта теорема достойна, во-первых, существования, и, во-вторых, признания её в нашем обществе.