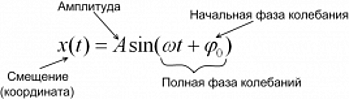круговая циклическая частота в чем измеряется

Угловая частота

Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:

Другое распространённое обозначение

Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:

См. также

Полезное

Смотреть что такое «Угловая частота» в других словарях:

угловая частота — периодических колебаний; угловая частота; отрасл. круговая частота Число периодов колебаний в 2π единиц времени. угловая частота синусоидального электрического тока; угловая частота Частота синусоидального электрического тока, умноженная на 2π … Политехнический терминологический толковый словарь

угловая частота — Скорость изменения фазы синусоидального электрического тока, равная частоте синусоидального электрического тока, умноженной на 2π. Примечание — Аналогично определяют угловые частоты синусоидальных электрического напряжения,… … Справочник технического переводчика

УГЛОВАЯ ЧАСТОТА — (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n число колебаний в 1 с., T период колебаний. Угловая частота при вращательном движении число оборотов, совершаемое вращающимся твердым телом за 1 с.,… … Современная энциклопедия

Угловая частота — (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n число колебаний в 1 с., T период колебаний. Угловая частота при вращательном движении число оборотов, совершаемое вращающимся твердым телом за 1 с.,… … Иллюстрированный энциклопедический словарь

угловая частота — 3.1.2 угловая частота w (angular frequency), рад/с: Циклическая частота, умноженная на 2π. Источник … Словарь-справочник терминов нормативно-технической документации

угловая частота — (круговая частота), число колебаний, совершаемых за 2π единиц времени. Угловая частота ω = 2πn = 2π/T, где ν число колебаний в единицу времени, Т период колебаний. Обычно используемая единица времени секунда; тогда угловая частота измеряется в … Энциклопедический словарь

угловая частота — kampinis dažnis statusas T sritis fizika atitikmenys: angl. angular frequency; cyclic frequency; radian frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f; циклическая частота, f pranc. fréquence… … Fizikos terminų žodynas

угловая частота — kampinis dažnis statusas T sritis automatika atitikmenys: angl. angular frequency; circular frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f pranc. fréquence angulaire, f; fréquence circulaire, f … Automatikos terminų žodynas

угловая частота — kampinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Virpesio fazės kitimo sparta, išreiškiama formule: ω = 2πf; čia f – dažnis. Kampinio dažnio ω matavimo vienetas yra rad/s (radianas per sekundę), o dažnio f – Hz (hercas) … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Циклическая частота колебаний

Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.

Это скалярная физическая величина.

Циклическая частота при гармонических колебаниях

Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.

Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:

Циклическую частоту колебаний можно выразить через период (T) колебаний:

Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:

Размерность циклической частоты:

Частные случаи формул для вычисления циклической частоты

Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:

Примером физического маятника является математический маятник. Круговая частота его колебаний равна:

Угловая частота затухающих колебаний находится как:

Примеры задач с решением

Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:

Максимальное значение скорости (амплитуда скорости) равна:

Ускорение точки вычислим как:

Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:

Вычислим циклическую частоту:

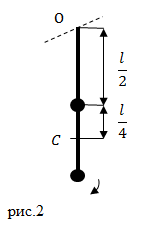
Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:

Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:

Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:

Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:

Источник

17. Механика Читать 0 мин.

17.547. Механические колебания

Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.

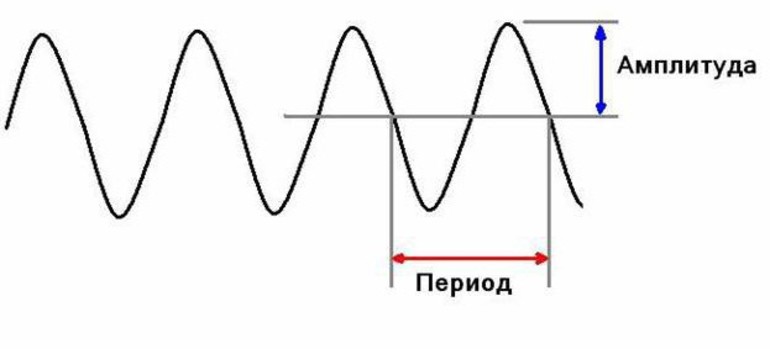
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.

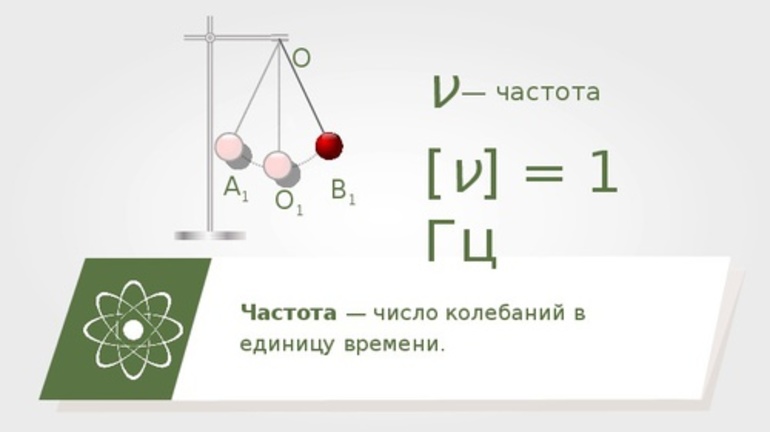
N ― количество колебаний;

ω ― циклическая частота [рад/с];

Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:

ω ― циклическая частота [рад/с];

φ0 ― начальная фаза колебаний, [рад];

Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.

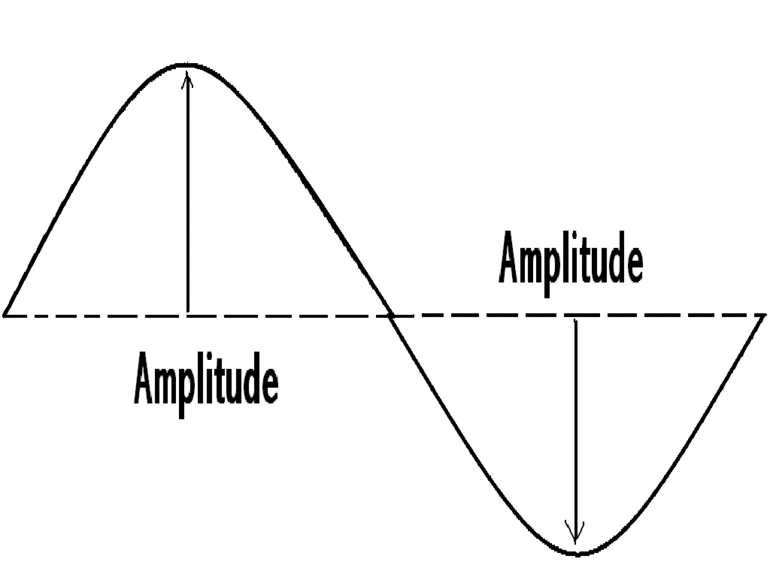
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.

Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.

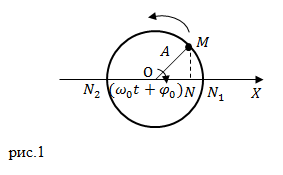
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где

φ ― полная фаза колебаний [рад];

φ0 ― начальная фаза колебаний, [рад];

ω ― циклическая частота [рад/с];

Пример анализа гармонических колебаний точки

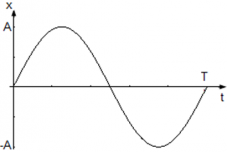
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где

ω ― циклическая частота [рад/с].

График колебания координаты точки имеет вид:

Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где

v ― скорость движения точки [м/с];

Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).

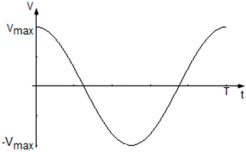
Уравнение скорости точки равно v(t) = Acos(ωt), где

v ― скорость движения точки [м/с];

ω ― циклическая частота [рад/с];

Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.

График колебания скорости точки имеет вид:

Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.

Ускорение ― это производная скорости по времени: a = vt‘, где

a ― ускорение движения точки [м/с2];

v ― скорость движения точки [м/с];

Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).

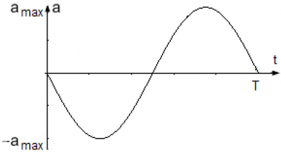
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где

a ― ускорение движения точки [м/с2];

ω ― циклическая частота [рад/с];

Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.

График колебания ускорения точки имеет вид:

Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где

E ― полная механическая энергия системы, E = const, [Дж];

EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];

EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].

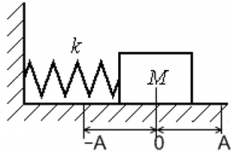
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).

EП ― потенциальная энергия деформированной пружины, [Дж];

k ― коэффициент упругости пружины [Н/м];

x ― деформация пружины (величина ее удлинения или сжатия) [м].

EП ― потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

ω ― циклическая частота [рад/с];

EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

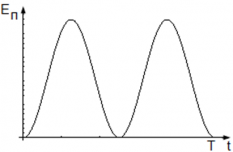
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.

График колебаний потенциальной энергии пружинного маятника:

Eк ― кинетическая энергия тела, [Дж];

v ― скорость движения тела, [м/с].

У тела, которое совершает колебательные движения, скорость ― переменная величина.

Eк ― кинетическая энергия маятника, [Дж];

ω ― циклическая частота [рад/с];

EКmax ― максимальная кинетическая энергия маятника, [Дж];

ω ― циклическая частота [рад/с].

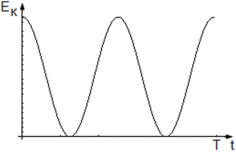
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.

График колебаний кинетической энергии маятника:

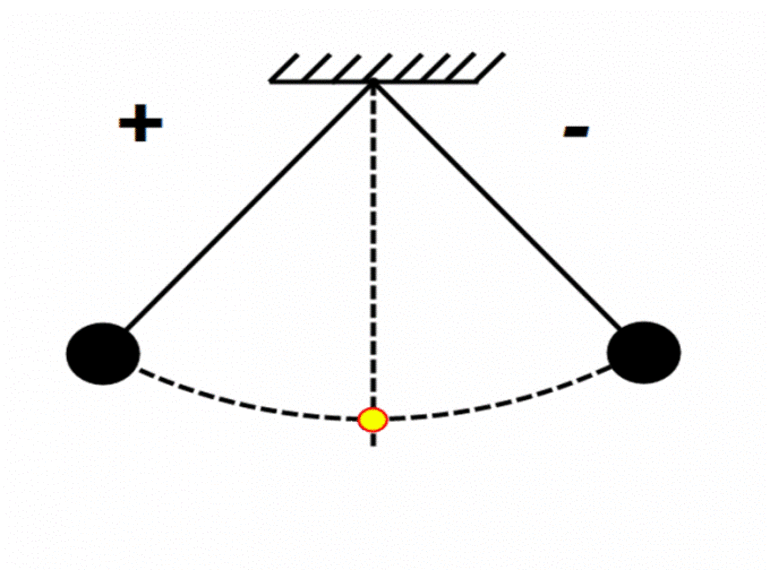
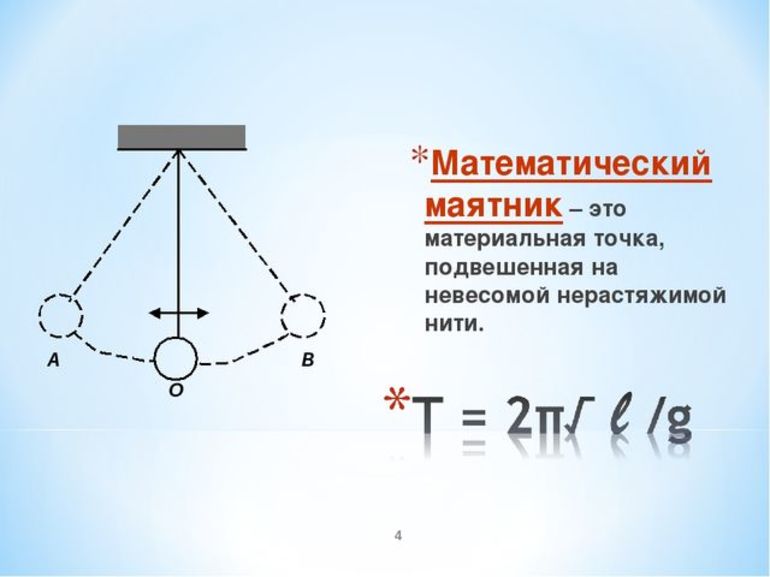
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.

l ― длина нити математического маятника [м];

g ― ускорение свободного падения [м/с2].

Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.

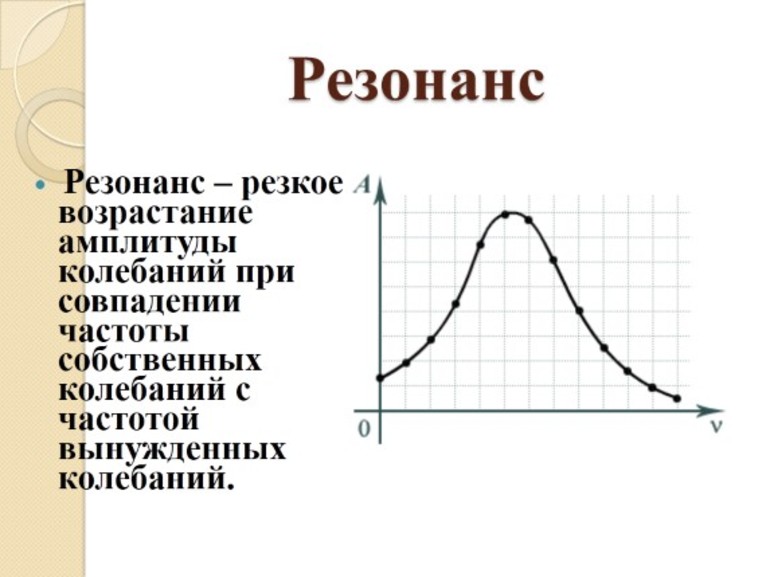
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.

На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.

Источник

Примеры движения

Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.

В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:

Амплитуда, период и частота

Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.

Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:

Выделяют понятие свободных колебаний. Когда системе, например, математическому маятнику, придают импульс, чтобы начать движение, дальнейшие его колебания (самостоятельные) будут считаться свободными.

Математический маятник

Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.

Также нить должна быть невесомой и нерастяжимой.

Груз в этом случае считается материальной точкой.

При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:

На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l

Вторая производная уравнения движения дает a=-(ω)^2x

Период: T=2π /ω T=2π*sqrt (g/l)

Это формула Галилея, которая описывает движение математического маятника.

Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.

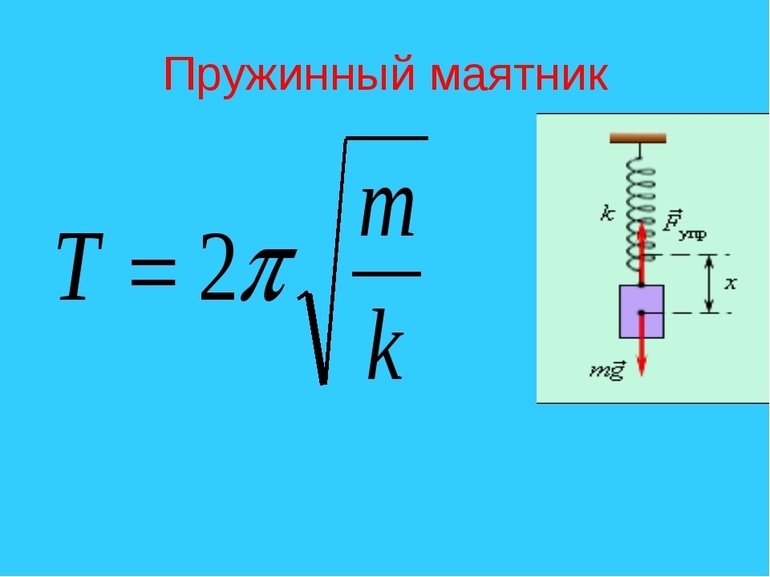
Пружинный маятник

Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.

Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.

Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:

Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.

По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.

После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.

Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.

Явление резонанса

Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.

Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.

В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.

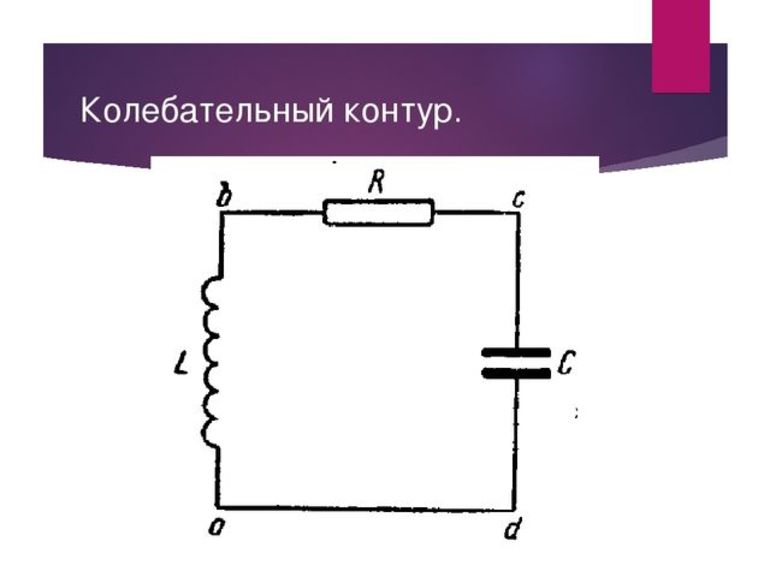
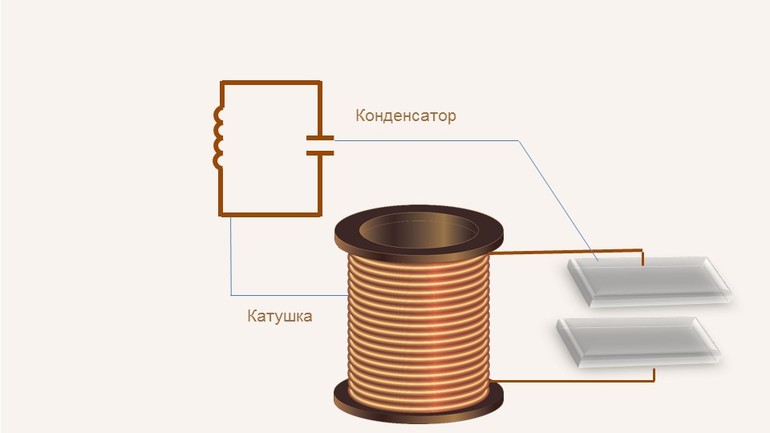
Колебательный контур

Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.

В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.

Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.

Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.

Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.

Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.

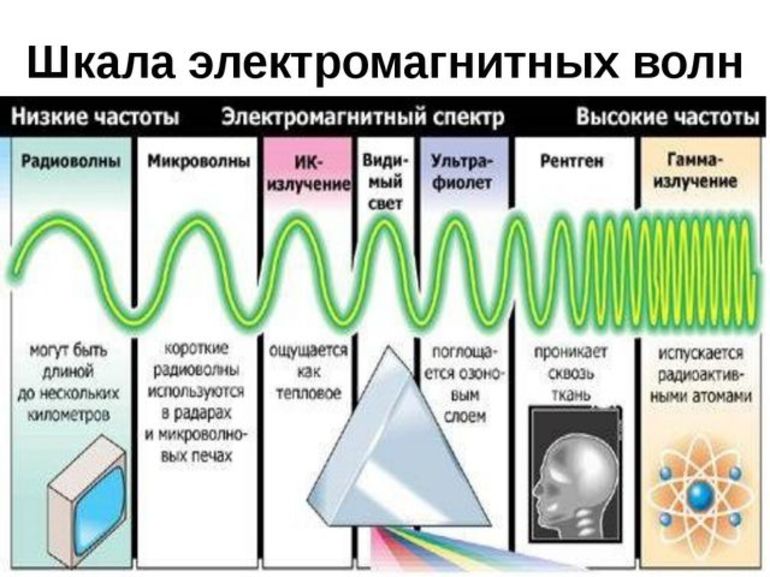
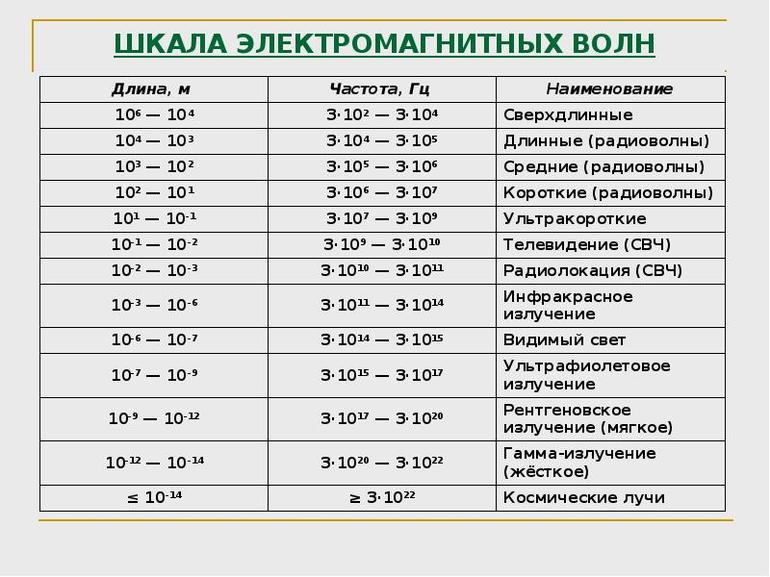
Звук и электромагнитные волны

Понятие частоты вводится и для звуковых и электромагнитных волн. Первые представляют собой колебания плотности среды. Вторые — изменение со временем напряженности магнитного и электрического полей.

От частоты звука зависит его тональность. Этим свойством пользуются для стандартизации описания музыки и создания музыкальных инструментов — каждой ноте соответствует своя частота.

До 16 Гц человеческое ухо не воспринимает, так же как и выше 20 КГЦ. Более высокие частоты используются в эхолокации, ультразвуковой диагностике.

Частота электромагнитных волн также определяет их способность взаимодействовать с человеческим организмом. Рентгеновское излучение проходит насквозь, при этом взаимодействуя с молекулами, вызывая их ионизацию. Ультразвук провоцирует процессы загара, фотосинтеза. Радиоволновое излучение практически не оказывает прямого воздействия, но хорошо подходит для передачи информации. В видимом диапазоне частота определяет цвет.

Есть также такая характеристика, как частота колебаний молекул. Она зависит от температуры тела и определяет его агрегатное состояние.

Таким образом, частота колебаний описывает большое количество процессов и оказывает воздействие на их характеристики.

Источник

Частота колебаний — определение, формулы и характеристики

Частота колебаний имеет следующее определение: это физическая характеристика, которая описывает количество повторений процессов в единицу времени. Для описания подобного движения вводятся и другие понятия: период, фаза, циклическая частота, амплитуда. Между всеми этими характеристиками имеется связь.

Примеры движения

Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.

В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:

Амплитуда, период и частота

Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.

Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:

Выделяют понятие свободных колебаний. Когда системе, например, математическому маятнику, придают импульс, чтобы начать движение, дальнейшие его колебания (самостоятельные) будут считаться свободными.

Математический маятник

Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.

Также нить должна быть невесомой и нерастяжимой.

Груз в этом случае считается материальной точкой.

При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:

На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l

Вторая производная уравнения движения дает a=-(ω)^2x

Период: T=2π /ω T=2π*sqrt (g/l)

Это формула Галилея, которая описывает движение математического маятника.

Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.

Пружинный маятник

Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.

Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.

Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:

Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.

По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.

После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.

Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.

Явление резонанса

Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.

Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.

В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.

Колебательный контур

Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.

В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.

Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.

Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.

Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.

Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.

Звук и электромагнитные волны

Понятие частоты вводится и для звуковых и электромагнитных волн. Первые представляют собой колебания плотности среды. Вторые — изменение со временем напряженности магнитного и электрического полей.

От частоты звука зависит его тональность. Этим свойством пользуются для стандартизации описания музыки и создания музыкальных инструментов — каждой ноте соответствует своя частота.

До 16 Гц человеческое ухо не воспринимает, так же как и выше 20 КГЦ. Более высокие частоты используются в эхолокации, ультразвуковой диагностике.

Частота электромагнитных волн также определяет их способность взаимодействовать с человеческим организмом. Рентгеновское излучение проходит насквозь, при этом взаимодействуя с молекулами, вызывая их ионизацию. Ультразвук провоцирует процессы загара, фотосинтеза. Радиоволновое излучение практически не оказывает прямого воздействия, но хорошо подходит для передачи информации. В видимом диапазоне частота определяет цвет.

Есть также такая характеристика, как частота колебаний молекул. Она зависит от температуры тела и определяет его агрегатное состояние.

Таким образом, частота колебаний описывает большое количество процессов и оказывает воздействие на их характеристики.

Источник