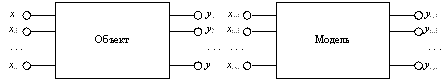косвенно измеряемые переменные характеризуются тем что

Косвенное измерение

Измерения как экспериментальные процессы весьма разнообразны. Это объясняется множеством экспериментальных величин, различным характером измерения величин, различными требованиями точности измерения и другие.

Наиболее распространена классификация видов измерений в зависимости от способа обработки экспериментальных данных. В соответствии с этой классификацией измерения делятся на прямые, косвенные, совместные и совокупные.

Содержание

Прямое измерение

Прямое измерение — это измерение, при котором искомое значение физической величины находится непосредственно из опытных данных в результате сравнения измеряемой величины с эталонами.

Косвенное измерение

Косвенное измерение — измерение, при котором искомое значение величины находится на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Совместное измерение

Совместное измерение — одновременное измерение нескольких неодноименных величин, для нахождения зависимости между ними. При этом решается система уравнений.

Совокупное измерение

Совокупное измерение — одновременное измерение нескольких одноименных величин, при котором искомые значения величин находятся решением системы уравнений, состоящих из результирующих прямых измерений различных сочетаний этих величин.

Полезное

Смотреть что такое «Косвенное измерение» в других словарях:

косвенное измерение — Определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Пример. Определение плотности D тела цилиндрической формы по результатам прямых… … Справочник технического переводчика

косвенное измерение — 3.6 косвенное измерение (indirect measurement): Измерение, посредством которого отдельные компоненты и/или группы компонентов, которые не присутствуют в рабочей эталонной газовой смеси, определяются, используя относительные коэффициенты… … Словарь-справочник терминов нормативно-технической документации

косвенное измерение — netiesioginis matavimas statusas T sritis automatika atitikmenys: angl. indirect measurement vok. indirekte Messung, f; mittelbare Messung, f rus. косвенное измерение, n pranc. mesurage indirect, m; mesure indirecte, f … Automatikos terminų žodynas

косвенное измерение — netiesioginis matavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydžio vertės radimas netiesioginiu būdu, kai ieškomoji vertė randama naudojant kitų dydžių tiesioginių matavimų rezultatus. pavyzdys( iai) Vienalytės medžiagos… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

косвенное измерение — netiesioginis matavimas statusas T sritis fizika atitikmenys: angl. indirect measurement vok. indirekte Messung, f rus. косвенное измерение, n pranc. mesure indirecte, f … Fizikos terminų žodynas

Косвенное измерение — 1. Измерение, при котором искомое значение величины определяют, исходя из результатов прямых измерений других величин, связанных с искомой величиной известной функциональной зависимостью Употребляется в документе: ОСТ 45.159 2000 Отраслевая… … Телекоммуникационный словарь

Косвенное измерение (вычисление) отдельных комплексных показателей функционирования ТОУ — Косвенное автоматическое измерение (вычисление) выполняется путем преобразования совокупности частных измеряемых величин в результирующую (комплексную) измеряемую величину с помощью функциональных преобразований и последующего прямого измерения… … Словарь-справочник терминов нормативно-технической документации

Косвенное измерение (вычисление) отдельных комплексных показателей Функционирования ТОУ — Кос во см ос автоматическое измерение (вычисление) выполняется путем преобразования совокупности частных измеряемых величии в результирукчцук» (комплексную) измеряем)» величину с помощью функциональных преобразований и последующего прямого… … Словарь-справочник терминов нормативно-технической документации

Измерение (физика) — Измерение совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением… … Википедия

Измерение — У этого термина существуют и другие значения, см. Измерение (значения). Измерение совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом… … Википедия

Источник

Полное меню

Основные ссылки

Вернуться в «Каталог СНиП»

МИ 2083-90 ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей.

ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ

ОПРЕДЕЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИИ И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ

КОМИТЕТ СТАНДАРТИЗАЦИИ И МЕТРОЛОГИИ СССР

ГСИ. ИЗМЕРЕНИЯ КОСВЕННЫЕ

Определение результатов измерений и оценивание их погрешностей

Дата введения 01.01.92

Настоящая рекомендация распространяется на нормативно-техническую документацию, содержащую методики выполнения косвенных измерений, и устанавливает основные положения определения результатов измерений и оценивание их погрешностей при условии, что аргументы, от которых зависит измеряемая величина, принимаются за постоянные физические величины; известные систематические погрешности результатов измерений аргументов исключены, а неисключенные систематические погрешности распределены равномерно внутри заданных границ ± θ.

Термины и определения, используемые в настоящей рекомендации, приведены в приложении 1.

1. ОБЩИЕ ПОЛОЖЕНИЯ

Функция f должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.

1.2. Результаты измерений аргументов и оценки их погрешностей могут быть получены из прямых, косвенных, совокупных, совместных измерений. Сведения об аргументах могут быть взяты из справочной литературы, технической документации.

1.3. При оценивании доверительных границ погрешностей результата косвенного измерения обычно принимают вероятность, равную 0,95 или 0,99. Использование других вероятностей должно быть обосновано.

1.4. Основные положения рекомендации устанавливаются для оценивания косвенно измеряемой величины и погрешностей результата измерения:

при линейной зависимости и отсутствии корреляции между погрешностями измерений аргументов (разд. 2);

при нелинейной зависимости и отсутствии корреляции между погрешностями измерений аргументов (разд. 3);

для коррелированных погрешностей измерений аргументов при наличии рядов отдельных значений измеряемых аргументов (разд. 4).

Примечание. Критерий проверки гипотезы об отсутствии корреляции между погрешностями измерений аргументов приведен в приложении 2.

2. КОСВЕННЫЕ ИЗМЕРЕНИЯ ПРИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ

Корреляция между погрешностями измерений аргументов отсутствует.

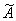
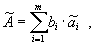
2.2. Результат косвенного измерения вычисляют по формуле

(3)

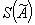
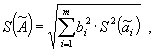
2.3. Среднее квадратическое отклонение результата косвенного измерения вычисляют по формуле

(4)

2.4. Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляют (без учета знака) по формуле

(5)

(6)

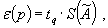
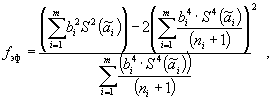
2.5. Границы неисключенной систематической погрешности результата косвенного измерения вычисляют следующим образом.

2.5.1. Если неисключенные систематические погрешности результатов измерений аргументов заданы границами θ _i ; то доверительные границы неисключенной систематической погрешности результата косвенного измерения Θ( p ) (без учета знака) при вероятности P вычисляют по формуле

(7)

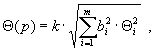
При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.

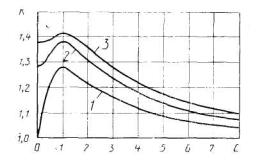
При доверительной вероятности Р = 0,99 поправочный коэффициент принимают равным 1,4, если число суммируемых составляющих m >4. Если же число составляющих m ≤4, то поправочный коэффициент k ≤1,4; более точное значение k можно найти с помощью графика зависимости

Погрешность, возникающая при использовании формулы ( 7 ) для суммирования неисключенных систематических погрешностей, не превышает 5 % (расчеты получены на основе анализа результатов композиций равномерных распределений).

(8)

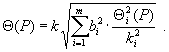
Для вероятности P = 0,95 k_i = 1,1; для Р = 0,99 значения коэффициентов k_i определяют в соответствии с п. 2.5.1.

2.6. Погрешность результата косвенного измерения оценивают на основе композиции распределений случайных и неисключенных систематических погрешностей.

2.6.1. Если 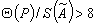, то за погрешность результата косвенного измерения принимают неисключенную систематическую составляющую погрешности измерения и ее границы вычисляют в соответствии с п. 2.5.

Значения коэффициента K в зависимости от отношения 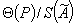для вероятности P = 0,95 и P = 0,99:

Источник

Переменные в математических моделях

Переменные величины, входящие в математическую модель, различают по нескольким признакам.

По роли, которую переменные играют по отношению к объекту моделирования. На рис. 1.4 X = (x₁, x₂,…, x_n) – вектор входных переменных, Y = (y₁, y₂,…, y_m) – вектор выходных переменных. В связи с разделением переменных на входные и выходные рассматриваются прямые и обратные задачи исследования объекта по его математической модели. В прямых задачах по данным о выходах объекта иссле-дуется его поведение в различных условиях (режимах работы), т. е.
входные переменные, структура и параметры модели относятся к исходным данным, а выходные переменные представляют результат исследования: Y =f(X) или F(X, Y) = 0, где известны характеристики X и f или F.

Рис. 1.4. Переменные в объекте и его модели

В обратных задачах считаются известными X и Y (доступны для измерения и исследования), а определению подлежат неизвестные структура и параметры модели (f или F). Такие задачи называют задачами идентификации.

Входные переменные разделяют на управляемые (управляющие воздействия) и неуправляемые (возмущения) Первые позволяют выполнять регулирование режима работы объекта, а вторые меняются самопроизвольно, например погодные условия.

По подверженности воздействию случайным факторам. Детерминированная (определенная) переменная означает, что для нее исключено влияние случайных факторов – она задается вполне определенным значением или меняется во времени по определенному закону. Некоторые переменные по своей природе или по влиянию на них случайных факторов являются случайными величинами. Процесс изменения такой величины во времени называется случайным или стохастическим процессом. К этим переменным можно отнести мощность нагрузки тяговой подстанции, которая зависит от загрузки контактной транспортной сети, или величину активного сопротивления провода ЛЭП, в большой степени подверженного влиянию температуры окружающей среды.

В основе описания случайных переменных лежат методы теории вероятностей, случайных процессов и математической статистики.

По свойствам непрерывности и дискретности. Изменения непрерывных переменных во времени описываются непрерывными функциями, которые могут принимать континуальное множество значений в некоторых практически всегда имеющихся пределах (рис. 1.5, а). Непрерывность, порожденная инерционностью материальных систем, является их неотъемлемым свойством. Однако на практике возможности разрешения близких значений функций и ее аргументов всегда ограничены; для каждого конкретного случая можно указать определенную область, в пределах которой эти значения становятся неразличимыми для наблюдателей или инструментальных средств. Очевидно, что такую область достаточно характеризовать единственным значением, что приводит к понятию дискретных переменных (рис. 1.5, б, в, г).

Дискретные переменные подразделяются на три типа:

1) дискретные относительно значений переменной (рис. 1.5, б);

2) дискретные относительно времени (рис. 1.5, в);

3) дискретные относительно значений переменной и относительно времени (рис. 1.5, г).

Множество дискретных значений, которые принимает переменная, как правило, является конечным: положение выключателя (включено, выключено), количество включенных генераторов на электростанции (0, 1, 2, … ), значения целых чисел, представленных в цифровой вычислительной машине (например, от –32 768 до +32 767). С помощью дискретных переменных относительно значений удобно представлять некоторые процессы (графики нагрузок или напряжений по часам
суток или месяцам года), распределение вероятностей (гистограмма)
и т. п.

Дискретность во времени связана с отсчетом или замером переменных в отдельные дискретные моменты времени. Так, в автоматизированных системах управления измерения переменных выполняются с заданной периодичностью, например, через каждые 5 минут.

Рис. 1.5. Виды переменных по свойствам непрерывности и дискретности

Дискретность по времени и по значению дополнительно к измерениям в отдельные моменты времени предполагает использование дискретных значений переменных.

По способу получения переменные подразделяются на наблюдаемые и ненаблюдаемые.

Главное свойство наблюдаемых переменных – доступность для наблюдения. Однако наблюдаемость сама по себе еще не обеспечивает возможности полного исследования и описания переменной. Необходимо, чтобы последняя обладала еще свойством измеримости, т. е. возможностью построения для исследуемой величины метрики. Этому требованию удовлетворяют непосредственно измеряемые переменные. Они представляют собой количественные характеристики свойств и параметров всевозможных материальных объектов и процессов (напряжение, ток, скорость, линейные размеры и пр.), которые определяются на основе прямого измерения, т. е. сравнения с мерой, обеспечены средствами измерения и охвачены существующей системой метрологического обеспечения.

Тесно связан с непосредственно измеряемыми и следующий класс переменных – косвенно измеряемые.

Косвенно измеряемая переменная x сама по себе не является объектом измерения, а часто и в принципе не может быть непосредственно измерена. Вместо нее непосредственному измерению подвергаются другие, вспомогательные переменные (α, β, γ,…), которые связаны с исследуемой переменной функциональной зависимостью x = f(α, β, γ,…). Это позволяет вычислить значение искомой переменной по результатам прямых наблюдений вспомогательных величин, например, вычислить объем тела по результатам измерения его линейных размеров. При испытаниях силовых трансформаторов в электрических сетях температуру его обмоток определяют методом измерения их сопротивлений постоянному току, т. е. температура – косвенно измеряемая переменная.

К косвенно измеряемым переменным относят такие искусственно сконструированные идеальные образования, которые вообще не наблюдаемы: математическое ожидание, дисперсия, энтропия и др.

Существует класс переменных, которые при их количественном оценивании не имеют материальной эталонной базы и находятся вне сферы метрологии. К ним относятся все виды непосредственно или косвенно измеряемых переменных, приведенных к безразмерной форме и выраженных в относительных единицах. Например, некоторые величины материальной природы (интенсивность сейсмических явлений, интенсивность облачности в метеорологии, твердость материалов по Бринеллю и некоторые другие), а также искусственные идеальные конструкции, характеризующие в количественном отношении сложные и массовые объекты и явления (рентабельность, прибыль, эффективность и др.). Такие переменные называют условно измеряемыми, так как меры или единицы измерения, используемые при их количественном оценивании, носят конвенционный характер.

Существует еще один класс наблюдаемых переменных – условно количественно оцениваемые. Они представляют сложные многофакторные явления, интенсивность которых может быть различной, но для количественного оценивания этой интенсивности не удается ввести ни объективной единицы измерения, ни способа измерения. Однако в целом ряде случаев между интенсивностями рассматриваемого явления удается установить отношение порядка (равны – не равны, больше – меньше и т. д.), а затем отобразить эти отношения, вообще говоря, произвольным образом на некоторое множество (систему) чисел. Результатом такой процедуры являются, например, численные оценки качества усвоения учащимися и студентами учебного материала, степень удовлетворения работой членов некоторого производственного коллектива, степень качества исполнения музыкального произведения или выполнения спортивного упражнения. Условное количественное оценивание основано на опыте и интуиции и по сути своей субъек-тивно.

Ненаблюдаемые переменные подразделяют на принципиально ненаблюдаемые и технически ненаблюдаемые.

Принципиально ненаблюдаемые переменные не существуют как компоненты реального мира и поэтому поддаются определению только косвенными методами, в частности на основе косвенных измерений (статистические характеристики).

Технически ненаблюдаемые переменные характеризуют такие материальные явления, которые либо не обеспечены техническими средствами, необходимыми для измерения и оценивания, либо протекают в условиях, когда инструментальный доступ к ним невозможен. Характерным примером переменной, не наблюдаемой из-за практической недоступности, является количество угля для помола в шаровой мельнице на электростанции.

Каждая переменная, связанная с материальным объектом, может изменять свои значения лишь в некоторых конечных пределах, которые обусловлены физическими свойствами объекта и характером решаемой задачи. Данные об этих пределах – ограничения на переменные – существенны при построении и использовании всех видов моделей, а в оптимизационных задачах, где необходимо найти оптимальное значение так называемой целевой функции, ограничения являются главной частью самой модели.

С математической точки зрения различают ограничения типа простых неравенств: X_min ≤ X ≤ X_max, Y_min ≤ Y ≤ Y_max – параллепипедные ограничения и функциональные ограничения, фиксирующие предельные значения некоторой величины в функции от других переменных: f_min(X) ≤ Z ≤ f_max(X) и т. п.

В практике моделирования выделяют так называемые жесткие ограничения, которые являются абсолютными (например, угол поворота лопатки турбины – «до упора»), и ограничения мягкие, допускающие кратковременные нарушения установленной границы значений переменной (например, верхнего предела рабочего напряжения на электродвигателе).

В общем случае данные об ограничениях на переменные входят в состав модели как обязательная составная часть.

1.4. Адекватность и эффективность
математических моделей

Математическое описание объекта может иметь различную степень соответствия (адекватность) объекту-оригиналу. Как правило, исследователь стремится к более полному и точному отражению в модели свойств объекта. Это естественное стремление объясняется неопределенностью, которая неизбежно присутствует при построении моделей. Нельзя заранее точно знать, какие свойства объекта важны для решаемой задачи, а какие – несущественны. Такая неопределенность тем больше, чем меньше исследователь знает исследуемый объект и меньше его опыт в решении подобных задач.

Таким образом, требование полноты соответствия модели объекту-оригиналу является одним из ее качеств. Мало того, излишняя полнота модели в большинстве случаев даже вредна, так как приводит к такому усложнению модели, что ее использование становится невозможным. Поэтому другое качество модели – это ее простота.

Нетрудно понять, что качества адекватности и простоты противоречат друг другу, т. е. с улучшением одного из них происходит ухудшение другого. Отыскание оптимального сочетания (как говорят, «золотой середины») этих двух качеств при построении модели есть
отдельная задача, решение которой лежит на исследователе. Здесь необходимы опыт, интуиция и соответствующий уровень подготовки исследователя. Идеальная квалификационная подготовка последнего не только весьма обширна, но и в значительной мере противоречива.

С одной стороны, исследователь должен досконально представлять себе задачу и глубоко изучить объект моделирования. Но, с другой стороны, исследователю, строящему модель, необходимо хорошо владеть аппаратом современной математики, представлять себе весь арсенал модельных конструкций, иметь опыт формализации знаний и использования современных вычислительных средств. Кроме того, во многих случаях от исследователя требуются знания в области планировании и проведения эксперимента на объекте-оригинале или на более сложной модели (вычислительный эксперимент).

Модель с оптимальным сочетанием качеств адекватности и простоты можно назвать эффективной (практически полезной) моделью. Математически такое сочетание соответствует максимуму так называемой «функции полезности», и, если эта функция может быть записана, отыскание ее максимума возможно известными оптимизационными методами.

Употребляя термин «точность математического моделирования», можно иметь в виду адекватность модели, например, говорят: точная или приближенная формула, линеаризованная (т. е. приближенно замененная линейной) зависимость и т. д. Но реализация математической модели, т. е. проведение «вычислителем» одного или нескольких расчетов, результатом которых будут численные значения переменной, вектора, таблицы, содержит погрешности вычислений из-за ошибок округления, прерывания итерационного процесса вычислений и ошибок в данных, которые переходят (распространяются) на результаты. Дальнейшая обработка реализаций математической модели предполагает и подсчет погрешности исследований. В связи с этим, рассматривая вопрос об эффективности математических моделей, следует иметь в виду погрешности реализаций, которые иногда являются причиной дополнительных упрощений модели, так как учет некоторых факторов может, например, сказаться на результатах в меньшей степени, чем погрешности в исходных данных.

Рассмотрим математическую модель линии электропередачи (ЛЭП) высокого напряжения. В нее входят такие параметры, как активное сопротивление, индуктивность самоиндукции и взаимоиндукции проводов, а также емкости между проводами и проводами и землей. Высота подвеса проводов и заземленных грозозащитных тросов на линии влияет на величину емкостей между проводами и землей. Следует ли в расчетах режимов ЛЭП учитывать близость земли? В некоторых случаях при достаточно длинных ЛЭП определение емкостных параметров требует уточнения в части влияния земли, а при небольших длинах линий это не обязательно.

При анализе адекватности, эффективности и точности отдельных математических моделей используются некоторые численные оценки. Получение этих оценок почти всегда связано с большими трудностями, так как требует проведения натурных (на объекте-оригинале) или вычислительных (по реализациям по более точной модели) экспериментов. Иногда такие эксперименты требуют больших материальных и временных затрат, но проводить их необходимо, поскольку это единственный способ оценить качество математических моделей.

Истинные значения параметров обычно отождествляются с экспериментально полученными. Однако погрешности натурного эксперимента во многих случаях оказываются соизмеримыми с погрешностями математических моделей, а иногда заметно их превышают.

Пусть на выходе объекта измеряются m переменных Y (рис. 1.4, а). При исследовании на математической модели получились m модельных переменных Y_м. Вектор погрешностей есть разница полученных векторов Δ = Y – Y_м. В целом погрешность математической модели можно оценить по норме вектора погрешностей Δ:

.

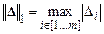
Часто используют евклидову норму и среднеквадратическую погрешность

.

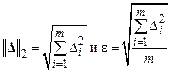
В качестве других характеристик математических моделей иногда называют экономичность (по затратам) и универсальность (применимость к группе объектов).

Источник