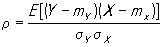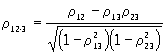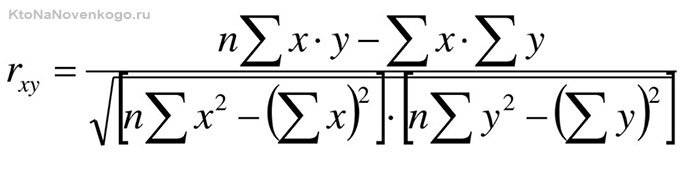корреляция что это простыми словами в медицине
Корреляция
Смотреть что такое «Корреляция» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
Корреляция
Корреля́ция (от позднелат. correlatio — соотношение)
термин, применяемый в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия, соотношения понятий, предприятий, предметов, функций. См. также Корреляция в математической статистике, Корреляция в биологии, Корреляция в лингвистике.
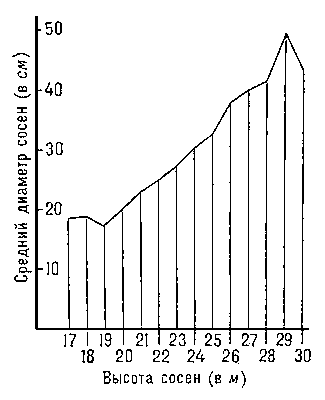
в математической статистике, вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия. Пример такого рода зависимости даёт корреляционная таблица. Из таблицы видно, что при увеличении высоты сосен в среднем растет и диаметр их стволов; однако сосны заданной высоты (например, 23 м) имеют распределение диаметров с довольно большим рассеянием. Если в среднем 23-метровые сосны толще 22-метровых, то для отдельных сосен это соотношение может заметным образом нарушаться. Статистическая К. в обследованной конечной совокупности наиболее интересна тогда, когда она указывает на существование закономерной связи между изучаемыми явлениями.
В основе теории К. лежит предположение о том, что изучаемые явления подчинены определённым вероятностным закономерностям (см. Вероятность, Вероятностей теория). Зависимость между двумя случайными событиями проявляется в том, что условная вероятность одного из них при наступлении другого отличается от безусловной вероятности. Аналогично, влияние одной случайной величины на другую характеризуется законами условных распределений первой при фиксированных значениях второй. Пусть для каждого возможного значения Х = х определено условное математическое ожидание у (х) = Е (YIX = х) величины Y (см. Математическое ожидание). Функция у (х) называется регрессией величины Y по X, а её график — линией регрессии Y по X. Зависимость Y от Х проявляется в изменении средних значений Y при изменении X, хотя при каждом Х = х величина Y остаётся случайной величиной с определенным рассеянием. Пусть mY = Е (Y) — безусловное математическое ожидание Y. Если величины независимы, то все условные математические ожидания Y не зависят от х и совпадают с безусловными:
Обратное заключение не всегда справедливо. Для выяснения вопроса, насколько хорошо регрессия передаёт изменение Y при изменении X, используется условная дисперсия Y при данном значении Х = х или её средняя величина — дисперсия Y относительно линии регрессии (мера рассеяния около линии регрессии):
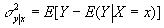
При строгой функциональной зависимости величина Y при данном Х = х принимает лишь одно определенное значение, то есть рассеяние около линии регрессии равно нулю.
Линия регрессии может быть приближённо восстановлена по достаточно обширной корреляционной таблице: за приближённое значение у (х) принимают среднее из тех наблюдённых значений Y, которым соответствует значение Х = х. На рисунке изображена приближённая линия регрессии для зависимости среднего диаметра сосен от высоты в соответствии с таблицей. В средней части эта линия, по-видимому, хорошо выражает действительная закономерность. Если число наблюдений, соответствующих некоторым значениям X, недостаточно велико, то такой метод может привести к совершенно случайным результатам. Так, точки линии, соответствующие высотам 29 и 30 м, ненадёжны ввиду малочисленности материала. См. Регрессия.
В случае К. двух количественных случайных признаков обычным показателем концентрации распределения вблизи линии регрессии служит корреляционное отношение
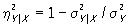
где 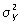
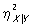
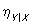
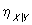
всегда —1 ≤ ρ ≤ 1. Однако практическое использование коэффициента К. в качестве меры зависимости оправдано лишь тогда, когда совместное распределение пары (X, Y) нормально или приближённо нормально (см. Нормальное распределение); употребление ρ как меры зависимости между произвольными Y и Х приводит иногда к ошибочным выводам, т. к. ρ может равняться нулю даже тогда, когда Y строго зависит от X. Если двумерное распределение Х и Y нормально, то линии регрессии Y по Х и Х по Y суть прямые у = mY+βY (x — mx) и х = mx+βx (у — mY), где 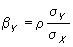
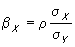
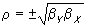
Так как в этом случае
то очевидно, что ρ (корреляционные отношения совпадают с ρ 2 полностью определяет степень концентрации распределения вблизи линий регрессии: в предельном случае ρ = ± 1 прямые регрессии сливаются в одну, что соответствует строгой линейной зависимости между Y и X, при ρ = 0 величины не коррелированы.
Корреляция между диаметрами и высотами 624 стволов северной сосны
| Диаметр, см | Высота, м | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Итого | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 14-17 | 2 | 2 | 5 | 1 | 10 | ||||||||||
| 18-21 | 1 | 3 | 3 | 12 | 15 | 9 | 4 | 47 | |||||||
| 22-25 | 1 | 1 | 1 | 3 | 18 | 24 | 29 | 14 | 7 | 98 | |||||
| 26-29 | 7 | 18 | 30 | 43 | 31 | 3 | 2 | 134 | |||||||
| 30-33 | 1 | 5 | 18 | 29 | 35 | 18 | 7 | 1 | 114 | ||||||
| 34-37 | 1 | 3 | 17 | 33 | 26 | 12 | 6 | 98 | |||||||
| 38-41 | 2 | 2 | 10 | 19 | 16 | 4 | 53 | ||||||||
| 42-45 | 4 | 13 | 6 | 8 | 1 | 32 | |||||||||
| 46-49 | 3 | 3 | 7 | 6 | 2 | 1 | 22 | ||||||||
| 50-53 | 1 | 4 | 4 | 2 | 1 | 12 | |||||||||
| 54-57 | 1 | 1 | 1 | 3 | |||||||||||
| 58 и более | 1 | 1 | |||||||||||||
| Итого | 4 | 6 | 9 | 16 | 41 | 57 | 86 | 108 | 124 | 91 | 55 | 24 | 2 | 1 | 624 |
| Средний диаметр | 18,5 | 18,6 | 17,7 | 20,0 | 22,9 | 25,0 | 27,2 | 30,1 | 32,7 | 38,3 | 40,0 | 41,8 | 49,5 | 43,5 | 31,2 |
При изучении связи между несколькими случайными величинами X1. Xn пользуются множественными и частными корреляционными отношениями и коэффициентами К. (последними по-прежнему в случае линейной связи). Основной характеристикой зависимости являются коэффициенты ρij — простые коэффициенты К. между Xi и Xj, в совокупности образующие корреляционную матрицу (ρij) (очевидно, ρij = ρji и ρkk = 1). Мерой линейной К. между X1 и совокупностью всех остальных величин X2. Xn служит множественный коэффициент К., равный при n = 3
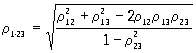
Если предполагается, что изменение величин X1 и X2 определяется в какой-то мере изменением остальных величин X3,. Xn, то показателем линейной связи между X1 и X2 при исключении влияния X3,. Xn; является частный коэффициент К. X1 и X2 относительно X3. Xn, равный в случае n= 3
Множественные и частные корреляционные отношения выражаются несколько сложнее.
В математической статистике разработаны методы оценки упомянутых выше коэффициентов и методы проверки гипотез об их значениях, использующие их выборочные аналоги (выборочные коэффициенты К., корреляционные отношения и т. п.). См. Корреляционный анализ.
Лит.: Дунин- Барковский И. В., Смирнов Н. В., Теория вероятностей и математическая статистика в технике (Общая часть), М., 1955; Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Хальд А., Математическая статистика с техническими приложениями, пер. с англ., М., 1956; Ван дер Варден Б. Л., Математическая статистика, пер. с нем., М., 1960; Митропольский А. К., Техника статистических вычислений, 2 изд., М., 1971.
Приближённая линия регрессии для зависимости среднего диаметра северной сосны от высоты.
стратиграфическая, сопоставление друг с другом одновозрастных слоев осадочных и вулканических горных пород и привязка их к подразделениям единой стратиграфической шкалы; сопоставление может охватывать как отдельные разрезы буровых скважин частных нефтеносных площадей или отдельных месторождений (углей, солей и др.), так и обширные площади и даже нескольких материков (телекорреляция и межконтинентальная К.). При К. используются всевозможные методы сопоставления — прослеживания маркирующих пластов и их пачек, данные каротажа, биостратиграфический метод, изотопные определения возраста горных пород (см. Геохронология). В результате К. составляется стратиграфическая схема, в левой части которой наносятся подразделения единой стратиграфической шкалы, а в правой — стратиграфическая схема отложений, встреченных в изучаемом районе.
в биологии, взаимозависимость строения и функций клеток, тканей, органов и систем организма, проявляющаяся в процессе его развития и жизнедеятельности. К. обусловливают развитие и существование организма как единого целого. Понятие К. было введено Ж. Кювье (1800—05), однако, не принимая эволюционного учения, он придал К. статичный характер: К. — свидетельство постоянства сосуществования органов.
Эволюционное учение придало К. динамический, исторический характер: взаимосвязь частей организма — результат как онтогенетический, так и филогенетический их развития. С эволюционных позиций проблема К. разрабатывалась А. Н. Северцовым; наиболее глубокое понимание её было дано И. И. Шмальгаузеном. Различается несколько форм К.: геномная К., обусловленная множественным действием наследственных факторов (Плейотропия), а также действием более тесно связанных между собой генов (хромосомная К.); морфогенетическая К. — взаимозависимость во внутренних факторах индивидуального развития. При этом имеет место связь между двумя или многими морфогенетическими процессами. Так, было показано, что зачаток хордомезодермы (См. Хордомезодерма) оказывается индуктором, определяющим развитие центральной нервной системы, глазной бокал индуцирует хрусталик и т. д. Морфогенетические К. определяют место и размеры развивающегося органа. Т. к. морфогенетические процессы приводят к изменению взаимоотношений органов, то возникают и новые морфогенетические К. Т. о., в процессе индивидуального развития постепенно развёртывается последовательная система морфогенетических К., которая оказывается одним из главных факторов Онтогенеза, поддерживающих в течение всего развития целостность организма. Данные, накопленные биологией развития (См. Биология развития), позволили некоторым авторам подразделить эти К. на ростовые К., зависящие от активности нервной системы, функциональные (эргонтические), гормональные и др. Филогенетические, или филетические, К. — соотносительные изменения органов в процессе эволюции организмов — А. Н. Северцов выделил как самостоятельное явление (см. Координация).
Лит.: Шмальгаузен И. И., Основы сравнительной анатомии позвоночных животных, 4 изд., М., 1947; его же, Организм, как целое в индивидуальном и историческом развитии, М.— Л., 1942; Северцов А. Н., Морфологические закономерности эволюции, М., 1949 (Собр. соч., т. 5); Balinsky В. Т., An introduction to embryology, 2 cd., Phil.— L., 1965.
в лингвистике, противопоставленность или сближение единиц языка по определённым свойствам (на всех уровнях языковой системы). Более всего развита теория фонологической К. (чередование фонем, с которым связано какое-либо морфологическое различие, или образующее соотносительные ряды, которые противополагаются по одному какому-либо различительному признаку). Различают понятия коррелятивной пары (франц. а — а, o — o, е — е, œ̃ — œ), признака (назализация во франц., лабиовеляризация в языках шона семьи банту), ряда (a, o, e,œ̃), пучка (в арчинском яз. шестичленный z — s — ts — ts’— `ts — `s ) и др.
Что такое корреляция и что означает коррелировать — простыми словами о сложном
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Когда некоторые люди слышат слово «корреляция», то зачастую просто впадают в ступор. Оно и понятно: жуткий термин из мира высшей математики и статистики.
Сразу представляются унылые графики, многоэтажные формулы, при взгляде на которые хочется забиться в угол и плакать. На самом деле все гораздо проще.
Потратив несколько минут на прочтение этой статьи, вы узнаете, что такое корреляция и как ее использовать в повседневной жизни.
Определение корелляции — что это
Простыми словами корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.
Объясним на примере: существует корреляция между температурой воздуха и потреблением мороженого. Чем жарче погода, тем больше холодного лакомства покупают люди. И наоборот.
Такие закономерности устанавливаются путем исследования больших объемов статистических данных. Собираем информацию о потреблении мороженого за несколько лет и сведения о колебаниях температуры за тот же период. А дальше сопоставляем и ищем зависимость.
Коррелировать – это значит быть взаимосвязанным с чем-то. Существует положительная и отрицательная корреляции.
При положительной чем больше один параметр, тем больше и другой. Например, чем масштабнее траты фермера на удобрения, тем обильнее урожай. При обратной корреляции рост одной величины сопровождается уменьшением другой. Чем выше здание, тем хуже оно противостоит землетрясениям.
Корреляция — это взаимосвязь без гарантий
Рассмотрим пример прямой корреляции: чем выше уровень благосостояния человека, тем больше его продолжительность жизни. Обеспеченные люди питаются качественной пищей и своевременно получают врачебную помощь. В отличие от бедняков.
Однако нельзя с уверенностью сказать, что определенный олигарх проживет дольше вот этого нищего.
Это лишь статистическая вероятность, которая может не сработать для одного конкретного случая. Этим корреляция отличается от линейной зависимости, где исход известен со 100-процентной вероятностью.
Но если мы возьмем выборку из сотни тысяч богачей и такого же числа малоимущих, сравним их продолжительность жизни, то общая тенденция будет верна.
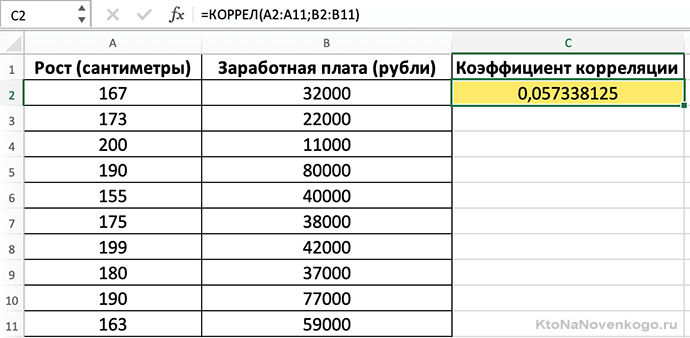
Коэффициент корреляции
Величина коэффициента корреляции рассчитывается по формуле:
Если внезапно потемнело в глазах и возникло непреодолимое желание закрыть статью (синдром гуманитария), то есть вариант попроще. Microsoft Exel все выполнит сам при помощи функции «КОРРЕЛ». Делается это так:
Судя по расчетам, рост человека практически никак не влияет на уровень зарплаты.
Реальные причины корреляции и возможные гипотезы
Курс доллара и стоимость нефти отрицательно коррелируют. Можем выдвинуть гипотезу: повышение цен на черное золото вызывает падение стоимости американской валюты. Но почему так происходит? Откуда взялась связь между этими явлениями?
Определение причины корреляции – это очень сложная задача. Переплетаются тысячи различных факторов, часть из которых скрыта.
Возможно, дело в том, что США – крупнейший потребитель нефти в мире. Каждый день они импортируют около 7,2 миллиона баррелей. Снижение цены на черное золото – хорошо для американской экономики, ведь позволяет тратить меньше денег. Следовательно, доллар растет.
Корреляция предоставляет возможность сделать вывод из статистических данных.
Например, мы выяснили, что существует отрицательная взаимосвязь между доходом персонала и его эффективностью в работе. Наша гипотеза: «Лентяи и бездельники получают больше, чем ответственные сотрудники». Тогда мы пересмотрим систему мотивации и избавимся от бесполезных людей.
Гипотеза – это лишь статистический вывод, предположение. Она вполне может оказаться ошибочной.
Согласно статистике, чем больше пожарных участвует в тушении огня, тем существенней размер ущерба. Какую гипотезу можем сделать отсюда? Пожарные приносят вред, давайте сократим их! Но если разобраться, то настоящая причина повреждения – это огонь. А увеличение числа лиц, задействованных в его тушении, – следствие масштаба пожара.
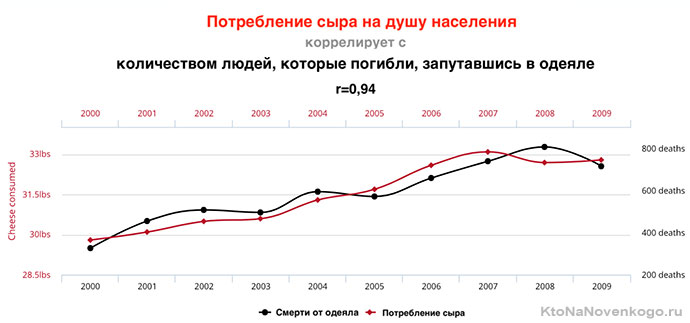
Наша вселенная бесконечна, а значит всегда можно найти несколько переменных, которые будут коррелировать между собой, несмотря на полное отсутствие причинно-следственных связей. Даже самое буйное воображение не сможет объяснить, что объединяет сыр и одеяло-убийцу:
Более подробно на эту тему смотрите в видео:
Как при помощи корреляции люди становятся богаче
Главное правило любого инвестора: не класть все яйца в одну корзину. Вложения рекомендуется диверсифицировать (что это?) – распределять. Поэтому люди покупают акции не одной компании, а десятка разных, формируя инвестиционные портфели. Если котировки какой-то фирмы упадут, то оставшиеся девять смогут отыграть падение или хотя бы уменьшить убытки.
Но это в теории, а на практике все портит корреляция. Проблема в том, что стоимости акций разных компаний внутри отрасли или даже всей страны могут сильно коррелировать. Проблемы огромной корпорации провоцируют панику на рынке, снижают стоимость иных активов, на первый взгляд не связанных между собой. В 2008 году случился крах Lehman Brothers, который вызвал цепную реакцию и обвал на мировых рынках.
Поэтому при инвестировании нужно стараться выбирать направления, которые не связаны между собой (r стремится к 0).
Территориальное приближение активов друг к другу усиливает корреляцию. Значит, нужно рассматривать варианты в разных точках мира, максимально удаленных друг от друга.
В жизни этот принцип тоже действует. Если ваши навыки и знания позволяют трудиться программистом, таксистом, сантехником и журналистом – вы хорошо защищены от риска безработицы.
Памятка
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (12)
Отличная статья! Спасибо! Все доступно к пониманию.
Скажите, пожалуйста, если некий факт N напрямую обусловлен фактом М, то есть без M не было бы N вообще, то корректно ли говорить о том, что N коррелирует с M?
Спасибо за статью. Кратко, четко, ясно.
«Корреляция — это взаимозависимость СЛУЧАЙНЫХ факторов. Она отображает ПРИБЛИЖЕННУЮ взаимосвязь и не дает точных ответов»
Выше цитата для Анны, т.е. «если некий факт N напрямую обусловлен фактом М,» то ИМХО это противоречит «взаимозависимости СЛУЧАЙНЫХ факторов» и «ПРИБЛИЖЕННОЙ взаимосвязи»
Все люди должны иметь хотя бы поверхностные знания об экономике, хотя многие ошибочно полагают, что их это не касается. В том числе важно понимать взаимосвязи между факторами, чтоб эффективно вести даже маленькое домохозяйство.
Не обязательно понимать сложные формулы корреляции, чтоб знать что безработица и стагнация сказываются на жизни всех граждан страны.
Это слово я слышала всего несколько раз за всю жизнь и каждый раз приходится гуглить. Ну почему нельзя давать определение проще? Напридумывают же сложных слов, а ты голову ломай.
Статья — супер! Спасибо большое.
Благодарю за статью. Доступно и понятно. Даже для тех у кого « синдром гуманитария»