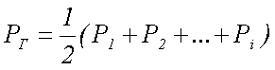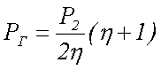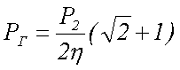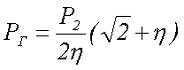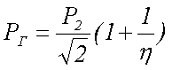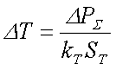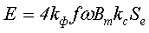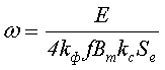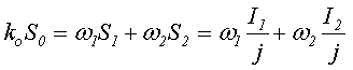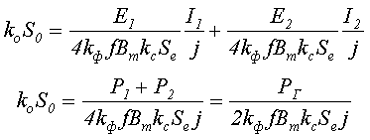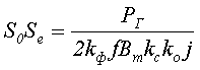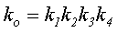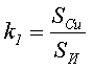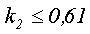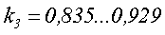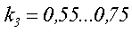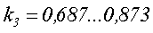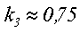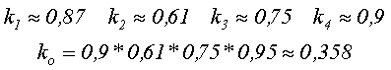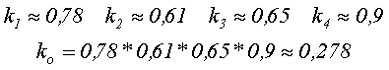коэффициент заполнения окна трансформатора что это
Коэффициент заполнения окна трансформатора что это
Трансформатор должен работать и не создавать проблем. Это его главная функция.
Исходя из этого, будем его и рассчитывать!
Прежде всего, необходимо уяснить для себя некоторую минимальную теорию.
Именно эти две неидеальности должны быть разумно-минимальными, чтобы трансформатор удовлетворял требованиям надежности.
Активное сопротивление обмоток и, как следствие, их нагрев, определяется заложенной при расчете плотностью тока в проводе. А по сему, ее значение должно быть оптимальным. На основании большого практического опыта рекомендую использовать значение плотности тока в медном проводе не более 3,2 ампера на квадратный миллиметр сечения. При использовании серебряного провода, плотность тока можно увеличить до 3,5 ампер на квадратный миллиметр. А вот, для алюминиевого провода она не должна превышать значение 2 ампера на квадратный миллиметр. Указанные значения плотности тока категорически превышать нельзя! И из этих значений мы выведем формулы для определения диаметра провода обмоток, коими будем пользоваться в расчете.
Большинство холоднокатаных электротехнических сталей сохраняют свою линейность до значения магнитной индукции 1,35 Тесла или 13500 Гаусс. Но надо не забывать, что напряжение в розетке электросети может иметь разброс от 198 до 242 вольт, что соответствует нормированному 10-и процентному отклонению от номинала как в плюс, так и в минус. То есть, если мы хотим, чтобы во всем диапазоне питающих напряжений наш трансформатор работал надежно, надо его рассчитать так, чтобы сердечник не подходил бы к нелинейности при любом допустимом напряжении питающей сети. В том числе и при 242 вольтах. А по сему, на номинальном напряжении 220 вольт, магнитная индукция должна выбираться не более 1,2 Тесла или 12000 Гаусс.
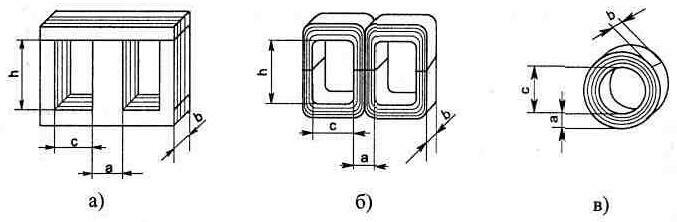
В настоящее время наиболее распространены магнитопроводы следующих конфигураций:
Дальнейший расчет трансформатора будем вести по строгим классическим формулам из учебника электротехники:
Разумеется, все это касается обычных силовых трансформаторов для ламповой или транзисторной аппаратуры, с выходными и питающими напряжениями до 1000 вольт, где не предъявляются повышенные изоляционные требования к обмоткам и к заделке их выводов.
3. Габаритная мощность трансформатора, в ваттах, на конкретно выбранном сердечнике определяется по формуле:
4. Задавшись напряжениями обмоток, количество необходимых витков можно рассчитать по такой формуле:
Если изначальные договоренности нами в точности соблюдены, и мы делаем жесткий трансформатор, то число витков как первичной, так и вторичной обмоток определяется по одной и той же формуле. Если же мы будем использовать трансформатор при предельном значении мощности для имеющегося типоразмера сердечника, рассчитанное по этой формуле, или мы проектируем маломощные трансформаторы (менее 50 Вт), с большим числом витков и тонким проводом обмоток, то число витков вторичных обмоток следует увеличить в 1/ η раз. С учетом нашей договоренности, это составит 1,05 или больше рассчетного на 5%.
Что же касается напряжений накальных обмоток, то здесь стоит вспомнить указание самой главной книги по радиолампам: «Руководство по применению приемно-усилительных ламп», выпущенное для радиоинженеров-разработчиков Государственным комитетом по электронной технике СССР в 1964 году.
Надо открыть это руководство на 13-ой странице, внимательно рассмотреть график на рисунке 1, и уяснить из него, что оптимальное напряжение накала радиоламп для сохранения их максимальной надежности и, соответственно, долговечности составляет 95% от номинала. Что для ламп с напряжением накала 6,3 вольта, составит ровно 6 вольт. Поэтому не надо увеличивать число витков накальных обмоток в 1,05 раза. Пусть будет, как есть.
5. Определяем токи обмоток:
Ток первичной обмотки: I1 = P / U1
При использовании двухполупериодного выпрямителя средний ток каждой половины обмотки будет в 1,41 раза (корень из двух) меньше, чем необходимый выпрямленный ток нагрузки. В случае использования мостового полупроводникового выпрямителя, ток обмотки будет в 1,41 раза больше, чем выпрямленный ток нагрузки. Поэтому, надо не забыть в формулы для определения диаметров проводов подставлять потребления по постоянному току, в первом случае поделенные, а во втором, умноженные на 1,41.
6. Рассчитываем диаметры проводов обмоток исходя из протекающих в них токов по следующим формулам (для меди, серебра или алюминия):
Полученные значения округляем в сторону увеличения до ближайшего стандартного диаметра провода.
Намотав трансформатор, для проведения дальнейших расчетов выпрямителя необходимо замерить некоторые его параметры.
Активное сопротивление первичной обмотки.
Активное сопротивление вторичных обмоток.
Ток холостого хода первичной обмотки (какой ток трансформатор потребляет из сети при отсутствии нагрузки на его вторичных обмотках).
На протяжении восемнадцати лет, не выключаясь, через этот трансформатор у меня питался «холостяцкий» холодильник «Саратов-II» (тот самый, при работе с которым сгорел автотрансформатор «Юг») после перевода нашего района на напряжение сети 220 вольт.
Для сравнения.
«Родная», промышленная, обмотка того самого трансформатора «Юг» на 220 вольт содержала 880 витков. Не удивительно, что он грелся как сволочь, даже будучи лишь автотрансформатором, и в конце-концов сгорел. Да, это и понятно, ведь, советская бытовая промышленность была заинтересована в увеличении покупательского спроса. Ну, вот и достигалось это не широкой номенклатурой товаров, а ограниченным сроком их работы!
ElectronicsBlog
Обучающие статьи по электронике
Как определить размеры трансформатора?
Всем доброго времени суток! Довольно часто у радиолюбителей возникают вопросы касающиеся определению размеров трансформатора. Зачастую они пользуются известными формулами связывающие сечение сердечника и мощность, которую передает трансформатор. Но зачастую данные выражения, которые можно встретить в сети, выведены под конкретную серию трансформаторов и не учитывают особенностей материала магнитопровода и обмоток. В данной статье я попробую раскрыть некоторые нюансы определения размеров сердечника.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Как определить габаритную мощность трансформатора?
В настоящее время основными критериями для разработки трансформатора является его минимальный размер и масса. Однако снижать габариты трансформатора можно лишь до некоторых пределов, которые ограничены допустимой рабочей температурой. Это связано с тем, что нагрев трансформатора зависит от потерь мощности в сердечнике и в обмотках, которые растут с уменьшением размеров трансформатора. Кроме этого перегрев связан с уменьшением площади теплоотдачи трансформатора.
В связи с этим для связи конструктивных и электромагнитных параметров трансформатора ввели понятие габаритной мощности трансформатора РГ, которая определяется как полусумма мощностей всех его обмоток
где Р1, Р2 и Рi – соответственно мощности первичной, вторичной и i-й обмотки трансформатора.
В случае наличия у трансформатора обмоток со средней точкой необходимо приводить такие трансформаторы к двухобмоточным. Выражения для определения габаритной мощности трансформатора в зависимости от типа обмоток приведены ниже.
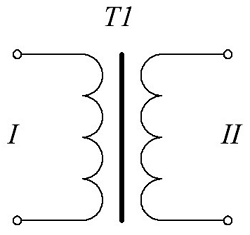
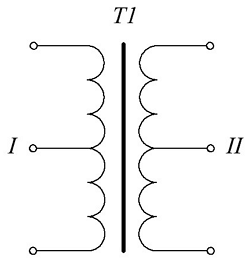
Для трансформатора с двумя обмотками без отводов
где Р1 – мощность поступающая на первичную обмотку,
Р2 – мощность снимаемая с вторичной обмотки,
η – КПД трансформатора.
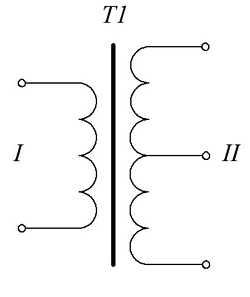
Для трансформатора с одной первичной обмоткой и одной вторичной обмоткой со средней точкой
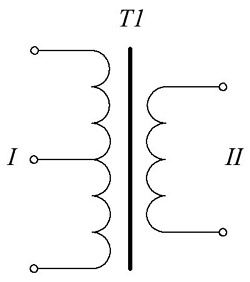
Для трансформатора с одной первичной обмоткой со средней точкой и одной вторичной обмоткой без отводов
Для трансформатора с одной первичной обмоткой со средней точкой и одной вторичной обмоткой со средней точкой
Как определить размер требуемого сердечника?
Как сказано выше, минимальные размеры трансформатора ограничены температурой перегрева трансформатора, на которую влияет потери мощности в самом трансформаторе. Определение минимальных размеров трансформатора в инженерной практике и радиолюбительстве является итерационным процессом, то есть задаются некоторые исходные данные (магнитная индукция, плотность тока и т.д.) и по ним вычисляют размер магнитопровода, после чего его проверяют на заданный перегрев.
Если полученное значение перегрева значительно отличается от требуемого, то уменьшают или увеличивают исходные данные и заново пересчитывают размеры сердечника. Такие пересчёты выполняют до тех пор, пока полученное значение перегрева не будет удовлетворять требуемому значению.
Тепловые расчёты трансформатора, в частности температуру перегрева ∆Т, выполняют аналогично как и для дросселя. Выражение для определения температуры перегрева имеет вид
где ∆Р∑ — суммарные потери мощности в трансформаторе, Вт,
Потери мощности определяются, так же как и для дросселя, но с учётом наличия нескольких обмоток трансформатора. Они зависят от размеров сердечника и свойств вещества, из которого он изготовлен.
Для определения размеров магнитопровода трансформатора используем закон электромагнитной индукции
где kф – коэффициент формы ЭДС,
f – частота изменения ЭДС,
ω – число витков обмотки трансформатора,
Bm – максимальное значение магнитной индукции в сердечнике,
Sc – площадь сечения сердечника трансформатора,
kс – коэффициент заполнения магнитопровода «сталью». Для ферритов kс = 1, для сердечников из листового материала при толщине ленты 0,35 – kс = 0,9…0,93, при толщине ленты 0,5 – kс = 0,93…0,95.
Преобразовав выражение, получим количество витков провода в обмотке трансформатора
Так как провод обмотки невозможно абсолютно плотно уложить в окно трансформатора, из-за множества факторов (использование круглого провода, наличие изоляции провода, межслоевой и межобмоточной изоляции), то необходимо ввести коэффициент заполнения окна kо, который в большинстве случаев не превышает kо = 0,3, а чаще всего составляет kо = 0,2…0,25. При этом, чем больше диаметр провода обмотки, тем меньше данный коэффициент.
Таким образом, заполнения окна магнитопровода обмоткой соответствует следующему выражению
где ko – коэффициент заполнения окна сердечника,
So – площадь окна сердечника,
w1, w2 – количество витков первичной и вторичной обмотки,
S1, S2 – площади сечения провода первичной и вторичной обмотки,
I1, I2 – действующая сила тока в первичной и вторичной обмотке,
Подставив в полученное выражение значение количества витков в обмотках получим
Таким образом, выбираемый сердечник должен иметь параметр произведения площадей больше чем расчётный.
Коэффициент использования окна сердечника
Одним из параметров, влияющих на размер сердечника, является коэффициент использования окна сердечника ko, показывающий какое количество меди появится в окне сердечника. На величину данного параметра влияет несколько факторов: толщина изоляции провода и межслоевая изоляция, тип намотки (рядовая или «внавал»), эффективная площадь окна сердечника и человеческий фактор (качество намотки). Поэтому коэффициент заполнения ko рассчитывается по следующей формуле
где k1 – коэффициент, учитывающий наличие изоляции проводника обмотки,
k2 – коэффициент, учитывающий размер слоя обмотки в окне сердечника,
k3 – коэффициент, учитывающий величину эффективной площади окна,
k4 – коэффициент, учитывающий влияние изоляции.
Данные коэффициенты различны для разных типов сердечников и обмоточного провода, рассмотрим их подробнее.
Коэффициент k1, на который влияет толщина изоляции в зависимости от диаметра провода может иметь значение k1 = 0,94…0,67.
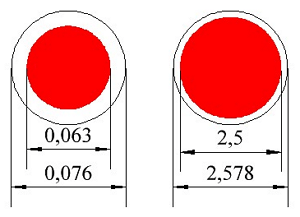
Сравнение относительной толщины изоляции проводов разного диаметра.
На рисунке показано примерное сечение обмоточных проводов различного диаметра. Видно, что чем больше диаметр провода, тем большую величину имеет коэффициент k1. Найти значение коэффициента k1 можно по следующей формуле
где SCu – площадь сечения провода «по меди»,
SИ – площадь сечения провода с изоляцией.
Коэффициент k2, называемый также коэффициентом заполнения обмоткой. Он учитывает плотность укладки витков относительно друг друга. При этом из практики известно, что реальная длина обмоточного провода оказывается на 10…15% больше расчётной длины. Размер слоя обмотки зависит от натяжения провода, его диаметра и техники укладки. Для разных типов намотки данные представлены ниже
| Диаметр провода, мм | Рядовая намотка | Намотка «внавал» |
| 0,0635…0,0863 | 0,85 | 0,75 |
| 0,096…0,109 | 0,86 | 0,8 |
| 0,124…0,0152 | 0,87 | |
| 0,17…0,267 | 0,88 | |
| 0,294…0,452 | 0,89 | |
| 0,505…2,67 | 0,9 | 0,9 |
Укладка провода может производится двумя способами: «квадратурным» и «гексагональным», сущность которых показана на рисунке ниже
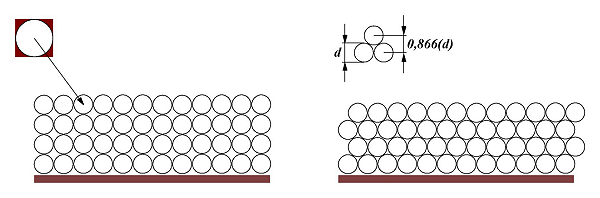
Способы укладки провода в слоях: «квадратурный» (слева) и «гексагональный» (справа).
При этом теоретические коэффициенты укладки составляют:
— для «квадратурного»: 0,785;
— для «гексагонального»: 0,907.
Данные коэффициенты практически не достижимы, а следовательно они еще меньше. Ещё одним фактором влияющим на данный коэффициент является эффект вспучивания и закругления обмотки при ее намотке на сердечник прямоугольного сечения
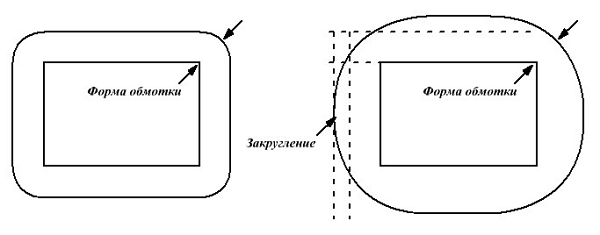
Проявление эффекта вспучивания и закругления обмотки на прямоугольном сердечнике.
На рисунке показано, как идеальная намотка на сердечник с прямоугольным сечение отличается от реального. Количественно эта величина выражается в 15…20 % увеличении толщины реальной обмотки по сравнению с идеальной.
Таким образом, коэффициент заполнения обмоткой составляет
Коэффициент k3, определяющий какая доля площади окна может быть занята обмоткой за исключением изолирующих материалов. Конструкция обмоток трансформатора предполагает наличие межслоевой и межобмоточной изоляции, а также изоляции обмоток от сердечника, называемой полями и в общем случае она имеет вид показанный ниже
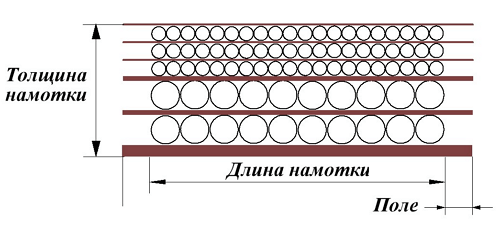
Обмотки трансформатора с изоляцией.
Размеры изоляции зависят от размера провода и имеет следующие размеры:
— для изоляционных полей от 1,57 до 6,35 мм;
— для межслойной изоляции от 0,013 до 0,254 мм.
В связи с этим значение коэффициента k3 для броневого ленточного сердечника
— для броневого ферритового сердечника
— для стержневого сердечника
— для тороидального сердечника
Коэффициент k4, характеризующий влияние изоляции, и учитывает наличие большого количества вторичных обмоток со значительным количеством изоляции. В результате каждая вторичная обмотка уменьшает значение коэффициента k4 на 5…10%.
В качестве примера вычислим значение коэффициента заполнения окна сердечника kо для некоторых видов трансформаторов.
Так для проводника диаметром d = 0,8 мм коэффициент заполнения окна в тороидальном ленточном сердечнике составит:
Для трансформатора выполненного на ферритовом Ш-образном сердечнике с обмоткой выполненной проводом диаметром d = 0,2 мм, обмотка намотана «внавал»:
Данные результаты являются расчётными, и на практике величина данного коэффициента получается несколько меньше.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
11. Методика расчета сетевого трансформатора
МЕТОДИКА РАСЧЕТА СЕТЕВОГО ТРАНСФОРМАТОРА
Целью расчета является получение заданных выходных параметров трансформатора (для сети с частотой 50 Гц) при его минимальных габаритах и массе.
Расчет трансформатора целесообразно начать с выбора магнитопровода, т. е. определения его конфигурации и геометрических размеров.
Наиболее широко распространены три вида конструкции магнитопроводов, приведенные на рис. 7.17.
Рис. 7.17. Конструкции магнитопроводов трансформаторов: а) броневого пластинчатого; б) броневого ленточного; в) кольцевого ленточного
Для малых мощностей, от единиц до десятков Вт, наиболее удобны броневые трансформаторы. Они имеют один каркас с обмотками и просты в изготовлении.
Трансформатор с кольцевым сердечником (торроидальный) может использоваться при мощностях от 30 до 1000 Вт, когда требуется минимальное рассеяние магнитного потока или когда требование минимального объема является первостепенным. Имея некоторые преимущества в объеме и массе перед другими типами конструкций трансформаторов, торроидальные являются вместе с тем и наименее технологичными (удобными) в изготовлении.
Исходными начальными данными для упрощенного расчета являются:
— напряжение первичной обмотки Ui;
— напряжение вторичной обмотки Uz;
— ток вторичной обмотки l2;
— мощность вторичной обмотки Р2 =I2 * U2 = Рвых
Если обмоток много, то мощность, отдаваемая трансформатором, определяется суммой всех мощностей вторичных обмоток (Рвых).
Размеры магнитопровода выбранной конструкции, необходимые для получения от трансформаторов заданной мощности, могут быть найдены на основании выражения:
Sст— сечение стали магнитопровода в месте расположения катушки;
Sок — площадь окна в магнитопроводе;
Вмах— магнитная индукция, см. табл. 7.5;
J — плотность тока, см. табл. 7.6;
Кок — коэффициент заполнения окна, см. табл. 7.7;
Кст — коэффициент заполнения магнитопровода сталью, см. табл. 7.8;
Величины электромагнитных нагрузок Вмах и J зависят от мощности, снимаемой со вторичной обмотки цепи трансформатора, и берутся для расчетов из таблиц 7.5 и 7.6.
Магнитная индукция Вмах, [Тл] при Рвых, [Вт]
Коэффициент заполнения стержня сталью формула
ElectronicsBlog
Обучающие статьи по электронике
Как определить размеры трансформатора?
Всем доброго времени суток! Довольно часто у радиолюбителей возникают вопросы касающиеся определению размеров трансформатора. Зачастую они пользуются известными формулами связывающие сечение сердечника и мощность, которую передает трансформатор. Но зачастую данные выражения, которые можно встретить в сети, выведены под конкретную серию трансформаторов и не учитывают особенностей материала магнитопровода и обмоток. В данной статье я попробую раскрыть некоторые нюансы определения размеров сердечника.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Как определить габаритную мощность трансформатора?
В настоящее время основными критериями для разработки трансформатора является его минимальный размер и масса. Однако снижать габариты трансформатора можно лишь до некоторых пределов, которые ограничены допустимой рабочей температурой. Это связано с тем, что нагрев трансформатора зависит от потерь мощности в сердечнике и в обмотках, которые растут с уменьшением размеров трансформатора. Кроме этого перегрев связан с уменьшением площади теплоотдачи трансформатора.
В связи с этим для связи конструктивных и электромагнитных параметров трансформатора ввели понятие габаритной мощности трансформатора РГ, которая определяется как полусумма мощностей всех его обмоток
где Р1, Р2 и Рi – соответственно мощности первичной, вторичной и i-й обмотки трансформатора.
В случае наличия у трансформатора обмоток со средней точкой необходимо приводить такие трансформаторы к двухобмоточным. Выражения для определения габаритной мощности трансформатора в зависимости от типа обмоток приведены ниже.
Для трансформатора с двумя обмотками без отводов
где Р1 – мощность поступающая на первичную обмотку,
Р2 – мощность снимаемая с вторичной обмотки,
Для трансформатора с одной первичной обмоткой и одной вторичной обмоткой со средней точкой
Для трансформатора с одной первичной обмоткой со средней точкой и одной вторичной обмоткой без отводов
Для трансформатора с одной первичной обмоткой со средней точкой и одной вторичной обмоткой со средней точкой
Как определить размер требуемого сердечника?
Как сказано выше, минимальные размеры трансформатора ограничены температурой перегрева трансформатора, на которую влияет потери мощности в самом трансформаторе. Определение минимальных размеров трансформатора в инженерной практике и радиолюбительстве является итерационным процессом, то есть задаются некоторые исходные данные (магнитная индукция, плотность тока и т.д.) и по ним вычисляют размер магнитопровода, после чего его проверяют на заданный перегрев.
Если полученное значение перегрева значительно отличается от требуемого, то уменьшают или увеличивают исходные данные и заново пересчитывают размеры сердечника. Такие пересчёты выполняют до тех пор, пока полученное значение перегрева не будет удовлетворять требуемому значению.
Тепловые расчёты трансформатора, в частности температуру перегрева ∆Т, выполняют аналогично как и для дросселя. Выражение для определения температуры перегрева имеет вид
где ∆Р∑ — суммарные потери мощности в трансформаторе, Вт,
Потери мощности определяются, так же как и для дросселя, но с учётом наличия нескольких обмоток трансформатора. Они зависят от размеров сердечника и свойств вещества, из которого он изготовлен.
Для определения размеров магнитопровода трансформатора используем закон электромагнитной индукции
где kф – коэффициент формы ЭДС,
ω – число витков обмотки трансформатора,
Bm – максимальное значение магнитной индукции в сердечнике,
Sc – площадь сечения сердечника трансформатора,
kс – коэффициент заполнения магнитопровода «сталью». Для ферритов kс = 1, для сердечников из листового материала при толщине ленты 0,35 – kс = 0,9…0,93, при толщине ленты 0,5 – kс = 0,93…0,95.
Преобразовав выражение, получим количество витков провода в обмотке трансформатора
Так как провод обмотки невозможно абсолютно плотно уложить в окно трансформатора, из-за множества факторов (использование круглого провода, наличие изоляции провода, межслоевой и межобмоточной изоляции), то необходимо ввести коэффициент заполнения окна kо, который в большинстве случаев не превышает kо = 0,3, а чаще всего составляет kо = 0,2…0,25. При этом, чем больше диаметр провода обмотки, тем меньше данный коэффициент.
Таким образом, заполнения окна магнитопровода обмоткой соответствует следующему выражению
где ko – коэффициент заполнения окна сердечника,
So – площадь окна сердечника,
w1, w2 – количество витков первичной и вторичной обмотки,
S1, S2 – площади сечения провода первичной и вторичной обмотки,
I1, I2 – действующая сила тока в первичной и вторичной обмотке,
Подставив в полученное выражение значение количества витков в обмотках получим
Таким образом, выбираемый сердечник должен иметь параметр произведения площадей больше чем расчётный.
Коэффициент использования окна сердечника
Одним из параметров, влияющих на размер сердечника, является коэффициент использования окна сердечника ko, показывающий какое количество меди появится в окне сердечника. На величину данного параметра влияет несколько факторов: толщина изоляции провода и межслоевая изоляция, тип намотки (рядовая или «внавал»), эффективная площадь окна сердечника и человеческий фактор (качество намотки). Поэтому коэффициент заполнения ko рассчитывается по следующей формуле
где k1 – коэффициент, учитывающий наличие изоляции проводника обмотки,
k2 – коэффициент, учитывающий размер слоя обмотки в окне сердечника,
k3 – коэффициент, учитывающий величину эффективной площади окна,
k4 – коэффициент, учитывающий влияние изоляции.
Данные коэффициенты различны для разных типов сердечников и обмоточного провода, рассмотрим их подробнее.
Коэффициент k1, на который влияет толщина изоляции в зависимости от диаметра провода может иметь значение k1 = 0,94…0,67.
Сравнение относительной толщины изоляции проводов разного диаметра.
На рисунке показано примерное сечение обмоточных проводов различного диаметра. Видно, что чем больше диаметр провода, тем большую величину имеет коэффициент k1. Найти значение коэффициента k1 можно по следующей формуле
где SCu – площадь сечения провода «по меди»,
SИ – площадь сечения провода с изоляцией.
Коэффициент k2, называемый также коэффициентом заполнения обмоткой. Он учитывает плотность укладки витков относительно друг друга. При этом из практики известно, что реальная длина обмоточного провода оказывается на 10…15% больше расчётной длины. Размер слоя обмотки зависит от натяжения провода, его диаметра и техники укладки. Для разных типов намотки данные представлены ниже
| Диаметр провода, мм | Рядовая намотка | Намотка «внавал» |
| 0,0635…0,0863 | 0,85 | 0,75 |
| 0,096…0,109 | 0,86 | 0,8 |
| 0,124…0,0152 | 0,87 | |
| 0,17…0,267 | 0,88 | |
| 0,294…0,452 | 0,89 | |
| 0,505…2,67 | 0,9 | 0,9 |
Укладка провода может производится двумя способами: «квадратурным» и «гексагональным», сущность которых показана на рисунке ниже
Способы укладки провода в слоях: «квадратурный» (слева) и «гексагональный» (справа).
При этом теоретические коэффициенты укладки составляют:
Данные коэффициенты практически не достижимы, а следовательно они еще меньше. Ещё одним фактором влияющим на данный коэффициент является эффект вспучивания и закругления обмотки при ее намотке на сердечник прямоугольного сечения
Проявление эффекта вспучивания и закругления обмотки на прямоугольном сердечнике.
На рисунке показано, как идеальная намотка на сердечник с прямоугольным сечение отличается от реального. Количественно эта величина выражается в 15…20 % увеличении толщины реальной обмотки по сравнению с идеальной.
Таким образом, коэффициент заполнения обмоткой составляет
Коэффициент k3, определяющий какая доля площади окна может быть занята обмоткой за исключением изолирующих материалов. Конструкция обмоток трансформатора предполагает наличие межслоевой и межобмоточной изоляции, а также изоляции обмоток от сердечника, называемой полями и в общем случае она имеет вид показанный ниже
Обмотки трансформатора с изоляцией.
Размеры изоляции зависят от размера провода и имеет следующие размеры:
— для изоляционных полей от 1,57 до 6,35 мм;
— для межслойной изоляции от 0,013 до 0,254 мм.
В связи с этим значение коэффициента k3 для броневого ленточного сердечника
— для броневого ферритового сердечника
— для стержневого сердечника
— для тороидального сердечника
Коэффициент k4, характеризующий влияние изоляции, и учитывает наличие большого количества вторичных обмоток со значительным количеством изоляции. В результате каждая вторичная обмотка уменьшает значение коэффициента k4 на 5…10%.
В качестве примера вычислим значение коэффициента заполнения окна сердечника kо для некоторых видов трансформаторов.
Так для проводника диаметром d = 0,8 мм коэффициент заполнения окна в тороидальном ленточном сердечнике составит:
Для трансформатора выполненного на ферритовом Ш-образном сердечнике с обмоткой выполненной проводом диаметром d = 0,2 мм, обмотка намотана «внавал»:
Данные результаты являются расчётными, и на практике величина данного коэффициента получается несколько меньше.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.