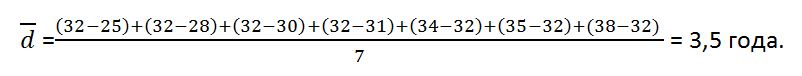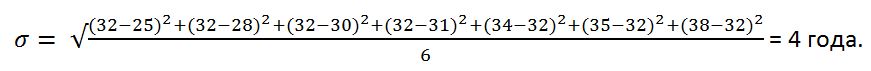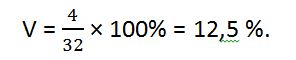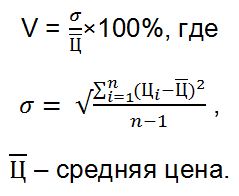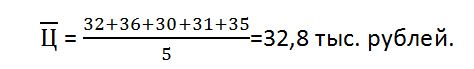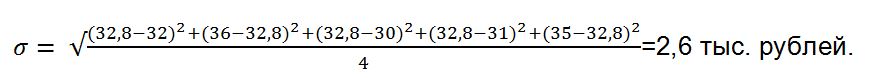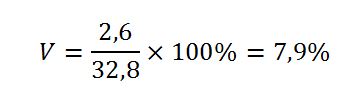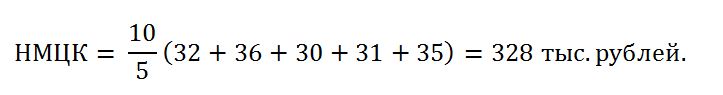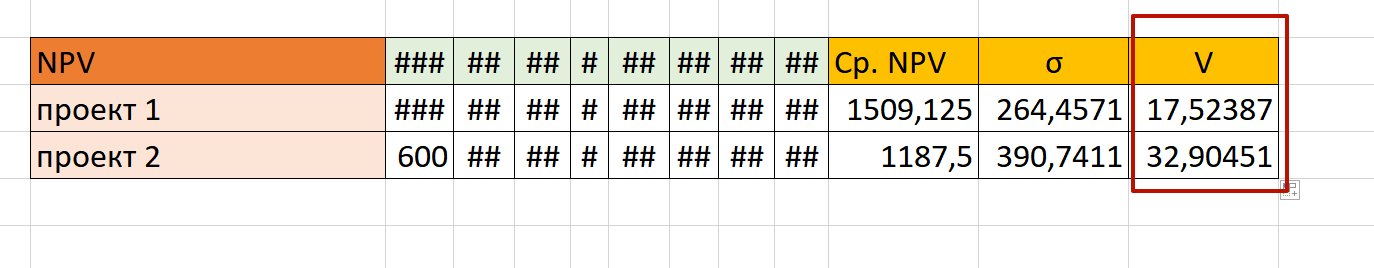коэффициент вариации признака равен 29 это означает что
Экспресс-подготовка к онлайн-тестированию:
для студентов дистанционного обучения, при устройстве на работу, прохождении аттестаций
Сдаешь тесты самостоятельно?
Закажи скайп-консультацию и узнай все секреты успешной сдачи экзаменов онлайн!
Статистика Тесты с ответами Тема 6-7-8
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 6. Средние величины
Какими способами возможно определить среднюю арифметическую взвешенную
методом наименьших квадратов
+прямым методом: как отношение суммы произведений значений признаков на их частоты к сумме частот
Что представляет собой распределительная средняя – мода
это средняя, занимающая среднее место в ряду и делящая его на две равные части
+это средняя, характеризующая центр распределения ряда
это средняя, показывающая распространение явления в среде
это средняя, характеризующая центр изменения явления в ряду
это средняя, характеризующая изменение явления в ряду
Что представляет собой распределительная средняя – медиана
это средняя, характеризующая центр изменения явления в ряду
это средняя, характеризующая центр распределения ряда
это средняя, показывающая распространение явления в среде
+это средняя, занимающая среднее место в ряду и делящая его на две равные части
это средняя, характеризующая изменение явления в ряду
Для каких целей определяется средняя антигармоническая
когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны
когда определяются суммарные значения признака
+когда необходимо рассчитать распределение явления в среде
когда рассматриваются «обратные» значения признака
когда требуется получить новые значения признака
Для каких целей определяется среднегармоническая
для выявления абсолютного значения явления
для выбора середины ряда
для выявления относительной величины ряда
для расчета темпов роста явления
+для определения среднего значения ряда динамики
В каких случаях рассчитывается среднегармоническая
когда требуется получить новые значения признака
когда определяются суммарные значения признака
когда необходимо рассчитать распределение явления в среде
+когда известны значения признака и произведение значений признаков ни их частоты, а сами частоты не известны
+когда рассматриваются «обратные» значения признака
В каких случаях рассчитывается степенная средняя
когда рассчитывается сумма произведений значений признаков на их частоты
когда определяется среднее значение нелинейного вида
+когда определяется среднее значение, выраженное функцией n-ого порядка
когда определяется среднее значение линейного вида
когда рассчитывается сумма произведений значений признаков n-ого порядка на их частоты
Тема 7. Показатели и анализ вариации
Что характеризует «размах вариации»
коэффициенты вариации ряда
+это разность между максимальным и минимальным значениями признака
Размах вариации (R) – это разность между …..и … значениями признака:
однородным и взвешенным
взвешенным и наименьшим
наибольшим и средним
средним и однородным
+наибольшим и наименьшим
Как определяется дисперсия альтернативного признака
как корень квадратный из произведения вероятностей признака, положенного в основу группировки на вероятность внешнего признака
как произведение вероятностей признака, положенного в основу группировки на вероятность внешнего признака
+как произведение вероятностей наличия признака и его отсутствия
как произведение межгрупповой и средней из внутригрупповых дисперсий
как отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий
Как определяется «среднеквадратическое отклонение»
как разность между максимальным и минимальным значениями признака
как средний квадрат отклонений индивидуальных значений признака от их средней величины
как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней
+как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
как средний коэффициент вариации ряда
Среднелинейное отклонение может быть:
Вариация признака изучается при помощи следующих показателей:
максимальный квадрат отклонений
+среднее линейное отклонение
произведение межгрупповой и средней из внутригрупповых дисперсий
отношение межгрупповой дисперсии к средней из внутригрупповых дисперсий
разность межгрупповой и средней из внутригрупповых дисперсий
+сумма межгрупповой и средней из внутригрупповых дисперсий
корень квадратный из произведения межгрупповой и средней из внутригрупповых дисперсий
Что характеризует межгрупповая дисперсия
случайную вариацию, полученную в результате действия случайных факторов
вариацию, полученную в результате действия внутренних факторов
вариацию, полученную в результате действия внешних факторов
вариацию, полученную в результате действия систематических и случайных факторов
+постоянную вариацию, полученную в результате действия систематических факторов
Как определяется «дисперсия»
как разность между максимальным и минимальным значениями признака
как средний коэффициент вариации ряда
+как средний квадрат отклонений индивидуальных значений признака от их средней величины
как корень квадратный из среднего квадрата отклонений индивидуальных значений признака от их средней величины
как среднеарифметическая из абсолютных значений отклонений отдельных вариантов от их средней
С какой целью рассчитывается «корреляционное отношение»
для выявления влияния группировки на исходный результат
для расчета дисперсии
+для выявления влияния признака, положенного в основу группировки на конечный результат
для выявления влияния группировки на показатели вариации
для обоснования необходимости представленной группировки
Как определяются коэффициенты вариации ряда
как разность между любым значением ряда и средней ряда
как разность между максимальным значением ряда и средней ряда
+как отношение показателя вариации к средней ряда
+как отношение любого показателя вариации к любой средней ряда
как отношение средней к показателю вариации ряда
Что означает «правило 3-сигм»
что при нормальном распределении значение признака не входит в зону 3-сигм
что при биномиальном распределении значения признака включается в зону 3-сигм
что при распределении Пуассона распределении значения признака не включается в зону 3-сигм
что при гипергеометрическом распределении значения признака включается в зону 3-сигм
+что вариация значений признака при нормальном распределении находится в пределах трех среднеквадратических отклонений
Тема 8. Измерение связи
Какая связь между явлениями называется функциональной
связь между явлениями отсутствует
связь между явлениями чисто внешняя, то есть с внешними явлениями
связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах
+связь между явлениями, в которых проявляются динамические закономерности (точная и полная)
В каких пределах изменяется индекс корреляции
в пределах от –1 до +1
в пределах от –2 до +2
+в пределах от 0 до +1
в пределах от –1 до 0
в пределах от 0 до –1
В каких пределах изменяется линейный коэффициент корреляции
в пределах от 0 до +1
в пределах от 0 до –1
+в пределах от –1 до +1
в пределах от –1 до 0
в пределах от –2 до +2
Как рассчитывается коэффициент Фехнера
как отношение разности числа пар с положительным отклонением от среднего уровня к сумме числа пар с отрицательным отклонением от среднего уровня
как отношение разности числа пар с различными знаками отклонений от средних уровней к сумме числа пар с одинаковыми различными знаками отклонений от средних уровней
как отношение суммы числа пар с отрицательным отклонением от среднего уровня к сумме числа пар с положительным отклонением от среднего уровня
как отношение разности числа пар с отрицательным отклонением от среднего уровня к сумме числа пар с положительным отклонением от среднего уровня
+как отношение разности числа пар с одинаковыми знаками отклонений от средних уровней к сумме числа пар с различными знаками отклонений от средних уровней
Какая связь между явлениями называется корреляционной
связь между явлениями чисто внешняя, то есть с внешними явлениями
связь между явлениями отсутствует
связь между явлениями, в которых проявляются динамические закономерности (точная и полная)
+связь между явлениями, в которых прослеживается статистическая закономерность в средних величинах
Коэффициент вариации признака равен 29 это означает что
— применение схемы простых процентов
— применение схемы сложных процентов
— обе схемы дают одинаковый результат
— нет верного ответа
— применение схемы простых процентов
— применение схемы сложных процентов
— обе схемы дают одинаковый результат
— нет верного ответа
— чем больше риск, тем меньше доходность
— чем больше риск, тем больше доходность
— независимо от риска доходность остается постоянной
— обыкновенные проценты с приблизительным числом дней предоставления ссуды
— точные проценты с приблизительным числом дней предоставления ссуды
— точные проценты с точным числом дней предоставления ссуды
— обыкновенные проценты с точным числом дней предоставления ссуды
— любых из упомянутых ставок;
— номинальных ставок, если речь идет о краткосрочных операциях.
— точного числа дней в году
— точного числа дней предоставления ссуды
— точного числа дней в году и приблизительного числа дней предоставления ссуды
— точного числа дней предоставления ссуды и приблизительного числа дней в году
— приблизительного числа дней предоставления ссуды
— приблизительного числа дней в году
— приблизительного числа дней в году и точного числа дней предоставления ссуды
— приблизительного числа дней предоставления ссуды и точного числа дней в году
— приведенную стоимость аннуитета и его срок;
— будущую стоимость аннуитета, его срок и ставку;
— приведенную и будущую стоимости аннуитета;
— срок аннуитета и ставку.
— сложных процентов для целого числа базисных периодов и простых процентов для дробной части базисного периода;
— сложных процентов для дробной части базисного периода и простых процентов для целого числа базисных периодов;
— сложных процентов для всей операции;
— простых процентов для всей операции.
— схема сложных процентов;
— схема простых процентов;
— схема простых процентов для целого числа кварталов и схема сложных процентов для
— дробной части квартала;
— любой предложенный вариант
— аннуитет с денежными поступлениями р раз в году;
— аннуитет сроком р лет;
— аннуитет, при оценке которого используется сложная процентная ставка с начислением процентов p раз за год;
— аннуитет, при оценке которого используется сила роста.
21. Средняя арифметическая простая величина равна:
— сумме произведений вариантов признака и частот, деленной на сумму частот;
— сумме всех значений признака, деленной на их число;
— корню степени n из произведения n вариантов признака.
22. Средняя арифметическая взвешенная величина равна:
— сумме произведений вариантов признака и частот, деленной на сумму частот;
— сумме всех значений признака, деленной на их число;
— корню степени n из произведения n вариантов признака.
23. Средняя геометрическая величина равна:
— сумме произведений вариантов признака и частот, деленной на сумму частот;
— сумме всех значений признака, деленной на их число;
— корню степени n из произведения n вариантов признака.
24. Формулу средней арифметической простой величины целесообразно применять, если:
— значения вариантов повторяются;
— необходимо рассчитать средний темп роста;
— информация задана в виде произведений вариантов и частот (объемов явлений);
— значения вариантов не повторяются.
25. Формулу средней гармонической величины целесообразно применять, если:
— значения вариантов повторяются;
— необходимо рассчитать средний темп роста;
— информация задана в виде произведений вариантов и частот (объемов явлений);
— значения вариантов не повторяются.
26. Формулу средней арифметической взвешенной величины целесообразно применять, если:
значения вариантов повторяются;
— необходимо рассчитать средний темп роста;
— информация задана в виде произведений вариантов и частот (объемов явлений);
— значения вариантов не повторяются.
27. Формулу средней геометрической величины целесообразно применять, если:
— информация задана в виде произведений вариантов и частот (объемов явлений);
— значения вариантов повторяются;
— необходимо рассчитать средний темп роста;
— значения вариантов не повторяются.
28. Среднее линейное отклонение характеризует:
— среднее значение квадрата отклонений вариантов признака от средней величины;
— среднее отклонение вариантов признака от средней величины;
— квадратный корень из среднего квадрата отклонений.
29. Дисперсия характеризует:
— среднее значение квадрата отклонений вариантов признака от средней величины;
— среднее отклонение вариантов признака от средней величины;
— квадратный корень из среднего квадрата отклонений.
30. Среднее квадратическое отклонение характеризует:
— среднее значение квадрата отклонений вариантов признака от средней величины;
— среднее отклонение вариантов признака от средней величины;
— квадратный корень из среднего квадрата отклонений.
31. Дисперсия признака равна 3600, коэффициент вариации равен 50%. Чему равна средняя величина признака?
32. Если коэффициент вариации составляет 25%, то совокупность
33. Значение признака, делящее данную совокупность на две равные части, в статистике называют
34. Колеблемость, многообразие, изменчивость значения признака у отдельных единиц совокупности называется:
35. Коэффициент вариации является ___________ показателем вариации
36. Определите дисперсию признака, если средняя величина признака равна 2600, а коэффициент вариации равен 30%
37. Размахом вариации называется: ________ максимального и минимального значений признака
— частное от деления
38. Средний квадрат отклонений индивидуальных значений признака от средней величины называется:
— средним квадратическим отклонением
— средним линейным отклонением
39. Уровень однородности статистической совокупности определяется значением
— среднего квадратического отклонения
40. Абсолютные показатели вариации:
— среднее квадратическое отклонение
41. Для значений признака: 3, 5, 6, 9, 11, 12, 13 мода равна
42. Для следующих значений признака: 3, 3, 3, 4, 4, 6, 7, 9, 9 мода равна
43. Имеется ряд распределения: Тарифный разряд рабочих: 2 3 4 5 6. Число рабочих: 8 16 17 12 7. Вид данного ряда:
44. К относительным показателям вариации относятся:
45. Медианой называется:
— наиболее часто встречающееся значение признака в данном ряду
— значение признака, делящее совокупность на две равные части
— различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени
— средняя взвешенная из варьирующих обратных значений признака
— Самое встречающееся значение признака в данном ряду
— значение признака, разделяющее совокупность на 2 равные части
— различие в значениях определенного признака у различных единиц данной совокупности в один и тот же период
— средняя взвешенная из варьирующих обратных значений признака
Что такое коэффициент вариации и для чего он нужен
Коэффициент вариации – это статистический показатель, какой широко используется в финансовых расчетах. Он показывает степень разброса значений в числовой последовательности. А именно, насколько любая из величин отклоняется от средней. Если вариация слишком высока, то оценивать среднее значение некорректно. В этой ситуации обыкновенно исключают минимальное и максимальное число.
Показатель чаще всего применяется при формировании начальной минимальной цены контракта по 44-ФЗ. Она должна опираться на выборке рыночных цен, а в их оценке как раз и используется вариация. Кроме того, применяется при анализе рисков инвестиционных проектов и доходности ценных бумаг. В цельном, показатели вариации применимы в любой сфере, где требуется оценить совокупность данных и их разнообразие: статистика, математика, экономический разбор, социология, маркетинг и т.д.
Формулы расчета в статистике
Для оценки совокупности значений и их однородности применяют следующие инструменты:
Рассмотрим применение указанных формул на примере оценки среднего возраста трудящихся в отделе кадров. В указанном подразделении трудятся 7 сотрудников, которым 25, 28, 30, 31, 34, 35 и 38 лет. Размах вариации покажет нам разницу в году между самым младшим и самым старшим из них:
Рассчитаем среднее линейное отклонение. Для этого для начала найдем посредственный возраст в отделе: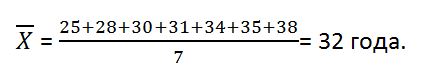
Соответственно, мы можем сказать, что средний возраст сотрудников составляет 32 ± 3,5 года.
Среднеквадратичное отклонение покажет то же самое, но немало точно:
Коэффициент вариации покажет, на сколько процентов возраст каждого работника отличается от среднего по отделу:
Оценка коэффициента вариации
Если со посредственными значениями и отклонениями от них все понятно, то зачем же рассчитывается коэффициент вариации? С его помощью можно судить, насколько показательно усредненное смысл и можно ли по нему судить о выборке в целом. В нашем примере он позволит ответить на вопрос, можно ли утверждать то, что посредственный возраст по отделу кадров составляет 32 года. Либо реальные показатели будут слишком сильно выделяться от полученного значения?
В статистике определены следующие критерии оценки:
Если показатель вариации превышает 33%, то выборка почитается неоднородной и судить о ней по средним значениям никак нельзя. При незначительном разбросе достоверность средних будет максимальной. В нашем образце вариативность средняя и в целом оценивать возраст по средним значениям с учетом отклонений вполне можно.
Если посмотреть на числовой ряд, то видать, что только 2 сотрудника существенно отклоняются от среднего возраста. На практике при слишком высокой вариативности из анализа исключают максимальное и минимальное смыслы, после чего проводят повторную проверку. Также часто по коэффициенту вариации сравнивают разные выборки. В нашем образце это слабо применимо, но, например, при анализе цен конкурентов будет вполне эффективно для выбора наиболее подходящей для анализа совокупности смыслов.
Читайте также! Выплата дивидендов учредителям ООО и АО в 2019 году
Применение при закупках по 44-ФЗ
Федеральный закон 44-ФЗ регулирует распорядок проведения государственных закупок. Его цель – не допустить злоупотреблений должностных лиц и передачу контрактов «своим» фирмам по завышенным/заниженным стоимостям. Именно для этого в законе определен порядок того, как устанавливается начальная минимальная цена контракта (НМЦК) – та, с какой и будут начинаться торги.
Методика определения начальной минимальной цены
Законом предусмотрено 5 методов определения НМЦК:
При этом наиболее предпочтительным и рекомендуемым является именно первоначальный. Его суть в том, что анализируются цены точно таких же товаров или услуг (идентичных) либо при их отсутствии схожих (однородных). Оба понятия четко установлены:
Данный порядок определен статьей 22 вышеуказанного закона. В 2019 году в нее было привнесено несколько изменений:
Как рассчитать НМЦК
Для расчета начальной цены заказчику необходимо составить выборку рыночных цен. Это можно сделать вытекающими способами:
Обычно используется первый способ. Нескольким поставщикам отправляются запросы введённой формы, а на основании полученных ответов и осуществляются расчеты по следующей формуле:
Коэффициент вариации в данном случае предзнаменований вид:
Пример расчета
Рассмотрим, как рассчитать НМЦК и коэффициент вариации на примере закупки 10 холодильников для больницы. От 5 поставщиков бывальщины получены коммерческие предложения со следующими ценами: 32, 36, 30, 31 и 35 тыс. рублей за штуку.
Оценим однородность ценовых предложений линией расчета коэффициента вариации. Для начала рассчитаем среднюю цену:
Теперь необходимо найти среднеквадратичное отклонение:
И, наконец, рассчитываем коэффициент вариации:
V меньше 10%, таким манером, делаем вывод о том, что выборка однородна и ее можно использовать для установки закупочных цен для торгов.
Посчитаем минимальную цену контракта:
Использование в оценке рисков
В финансовом разборе степень отклонения показателя от среднего значения показывает уровень риска. Например, если прибыль в разные годы существования компании то существенно всходит, то падает в убыток, инвестировать в нее опасно. То же самое касается ценных бумаг и любых других биржевых инструментов. Самыми привлекательными будут стабильные бумаги с минимальными колебаниями котировок при неплохом росте. Таким образом, есть еще два направления, где активно используется коэффициент вариации: оценка рисков проекта и рисков по доходности ценных бумаг.
Декламируйте также! Организация и внедрение бережливого производства на предприятии
Инвестиционные проекты
Как правило, при оценке рисков инвестиционных проектов используются:
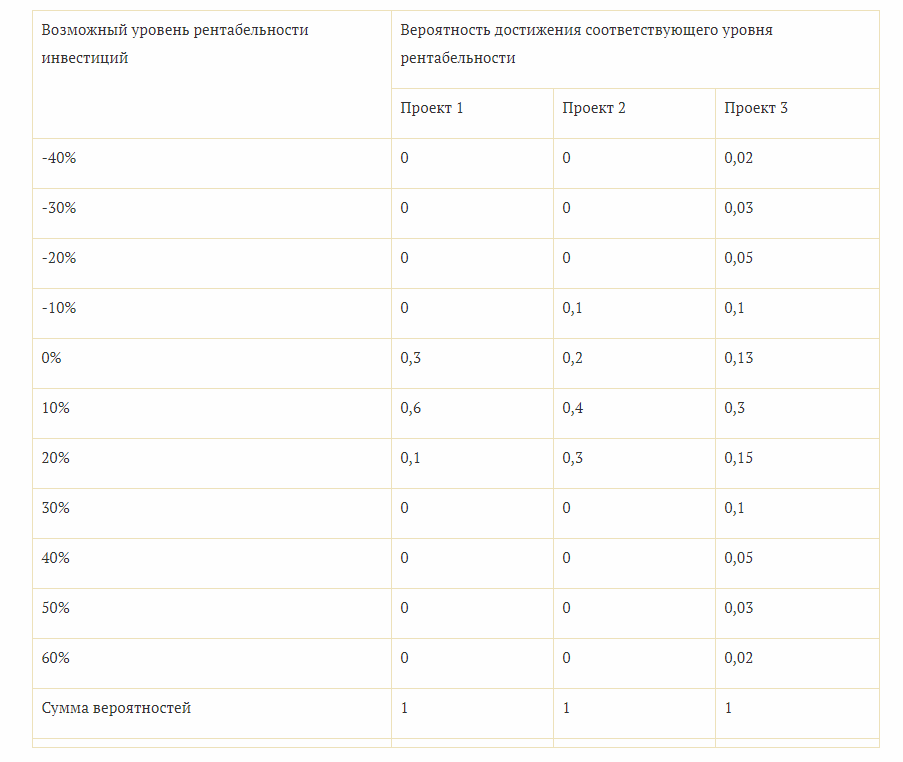
Обычно сравниваются несколько проектов по всем критериям. Также есть вариант рассмотреть возможность достижения того или другого уровня рентабельности:
В данном случае все проекты будут рискованными, поскольку коэффициент вариации составит 65%, 95% и 198% соответственно. Но риск по первому немало чем в 2 раза ниже, чем по третьему, поэтому из представленных вариантов лучше выбрать его.
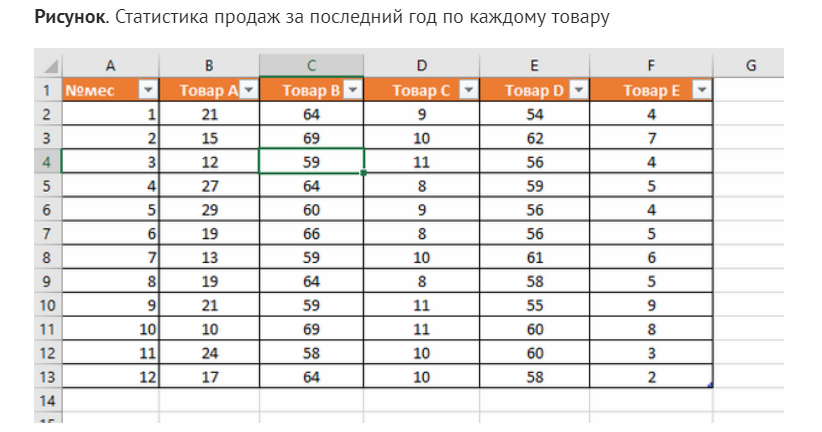
Нередко используют коэффициент при анализе спроса и принятии решении о закупках. Так, анализируется статистика продаж товара, после чего определяется, что закупать в первую очередь, а что только при наличии предзаказа:
В этом примере коэффициенты вариации по товарам А, B, C, D и E будут равны 30%, 6%, 12%, 4%, 38% соответственно. Очевидно, что спрос на продукцию E нестабилен и мощно колеблется в разные месяцы, поэтому заказывать целую партию рискованно.
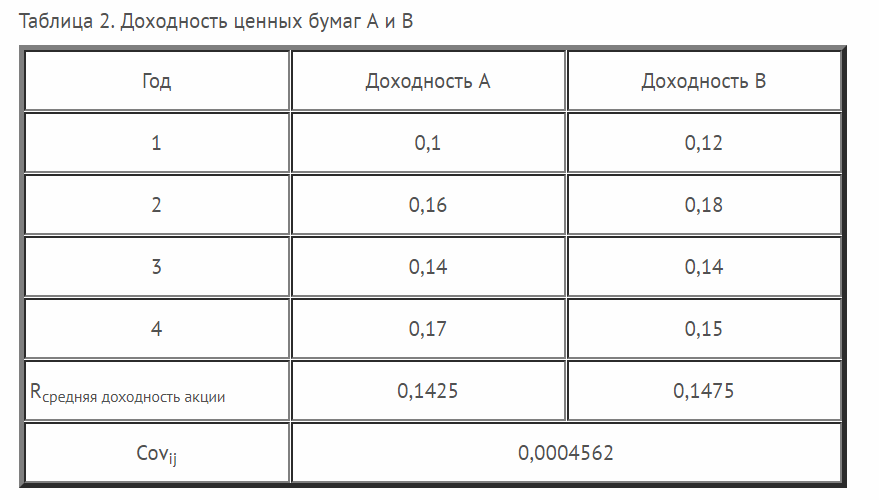
Ценные бумаги
Что касается торговли на бирже, то тут можно оценивать в двух вариантах:
В первом случае, имея эти о колебаниях котировок в прошлом, мы сможем оценить риск вложения именно в данный инструмент. Во втором варианте можно оценить риск портфеля инвестиций на основании совокупности доходности любой его составляющей. Также риск портфеля можно проанализировать на основании совокупности вариаций каждой его составляющей во временном интервале. Все эти методики используются в комплексном анализе рисков инвестиционного портфеля.
Расчет в MS Excel
Как при расчете цены контракта, так и при оценке инвестиционных проектов выполнять громоздкие вычисления квадратичного отклонения и коэффициента вариации вручную весьма трудоемко. Поэтому рассмотрим, как быстро и просто выполнить это при помощи электронной таблицы Excel.
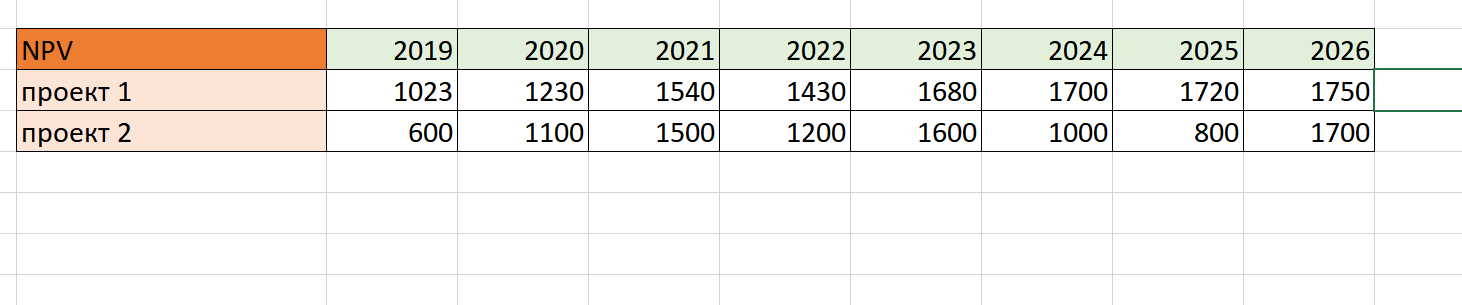
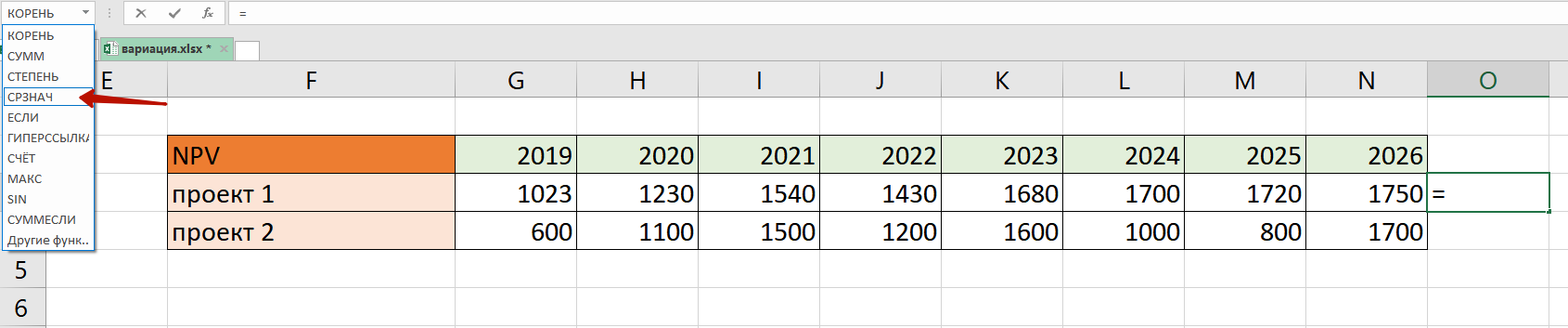
Для начала открываем редактор и создаем таблицу с отправными данными. Для примера возьмем два инвестиционных проекта с показателями NPV за 8 лет.
Далее находим среднее значение прибыли при помощи функции СРЗНАЧ:
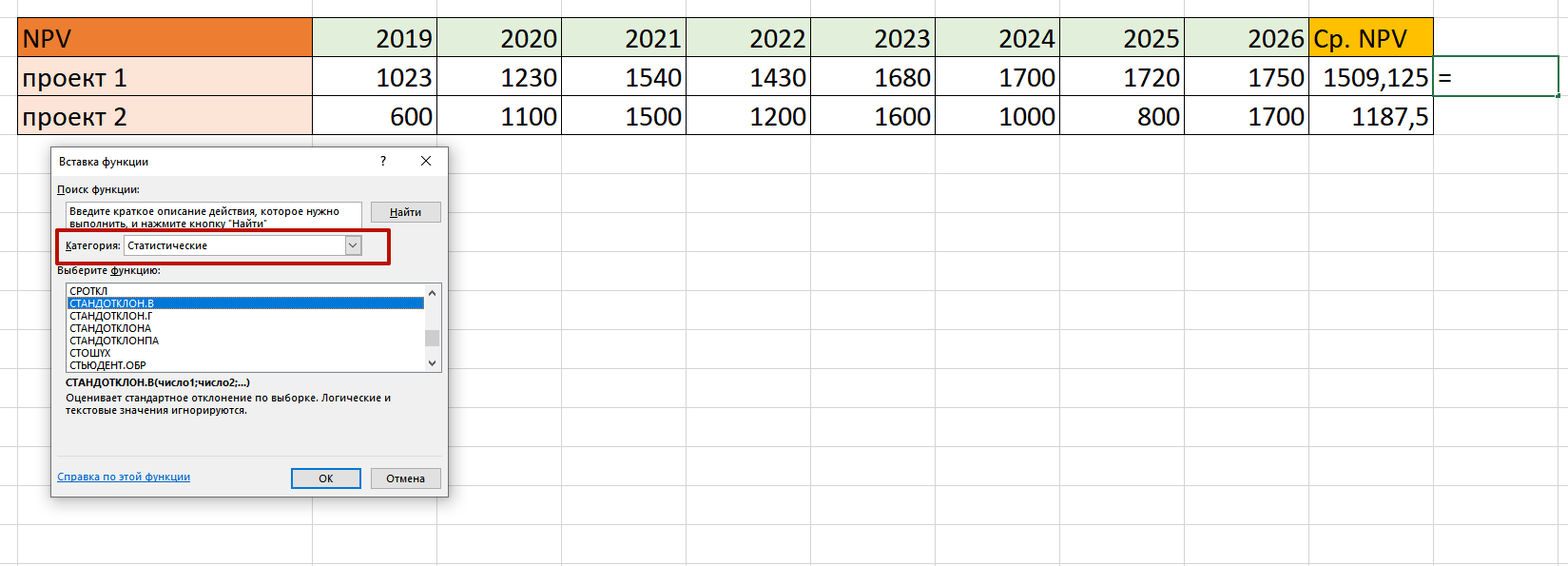
Вышли вот такие значения:
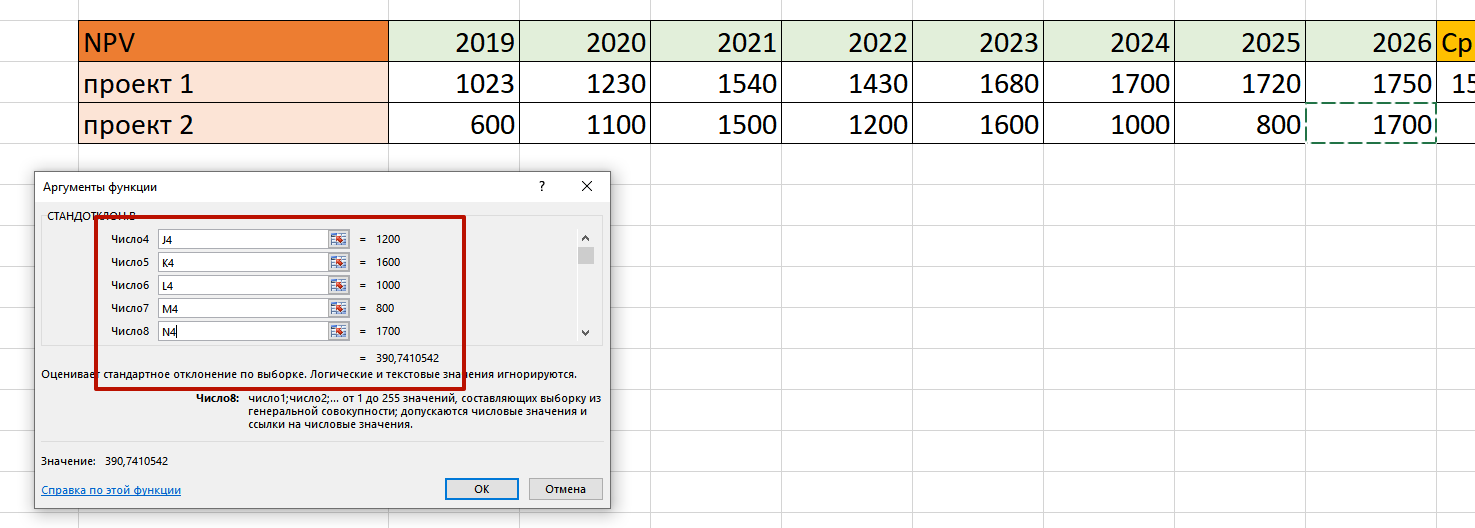
Теперь необходимо вычислить среднеквадратичное отклонение. Для этого предназначена функция СТАНДОТКЛОН.В
Обратите внимание, что в любую строку необходимо вбить одну ячейку, а не выбирать весь диапазон:
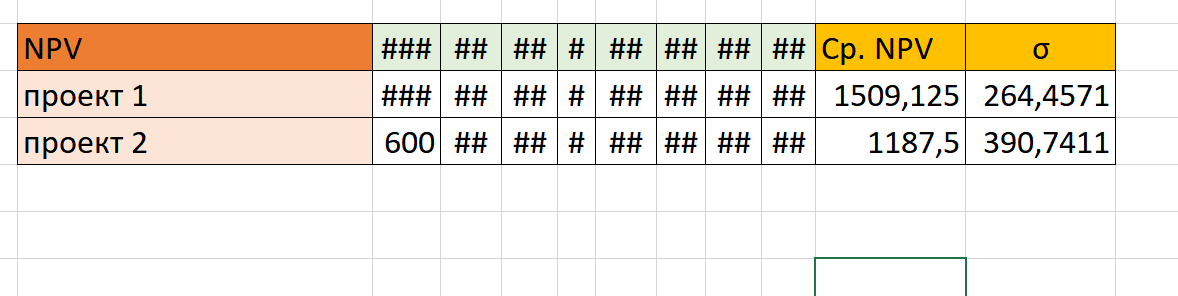
Таким образом, у нас есть рассчитанные посредственные значения доходности и среднеквадратичного отклонения по двум проектам:
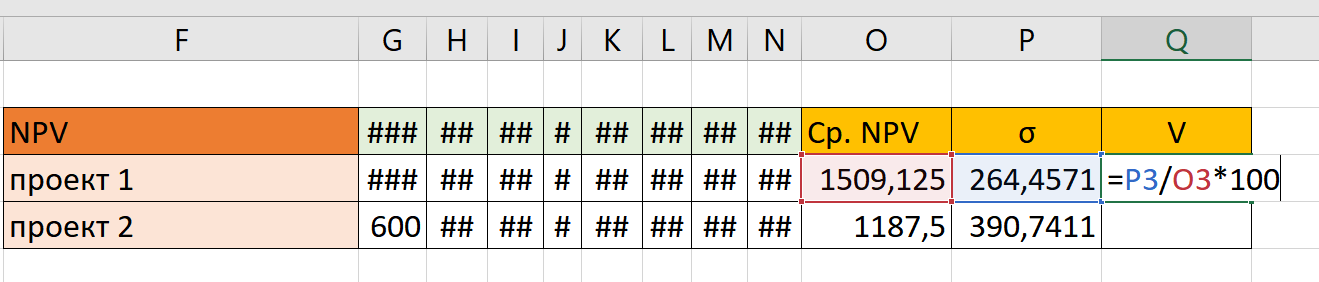
Теперь нам нужно найти коэффициент вариации. Для этого мы попросту вписываем вручную формулу: ячейку σ делим на среднюю доходность и умножаем на 100:
Таким образом, получаем следующие смыслы коэффициента вариации:
Можно сделать вывод о том, что первый проект менее рисковый, чем второй.