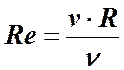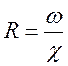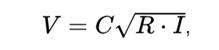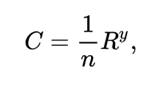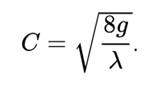коэффициент шези в чем измеряется

Для определения режима движения жидкости расчетным путем.

3. Как определить режим движения воды в напорном трубопроводе по числу Рейнольдса?

4. Поясните формулы 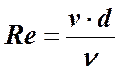и

v – средняя скорость потока,

ν – кинематический коэффициент вязкости жидкости, м2/с.

для определения режима движения жидкости в круглых напорных трубах используется число Рейнольдса в виде

,где гидравлический радиус заменен внутренним диаметром трубы d.

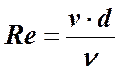
5. Поясните смысл выражения

— гидравлический радиус живого сечения потока где ω-площадь живого сечения потока χ-смоченный периметр

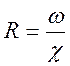
6. Что такое гидравлический радиус?

7. Что такое смоченный периметр?

— гидравлический радиус живого сечения потока где ω-площадь живого сечения потока χ-смоченный периметр

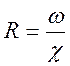
Длиной смоченного периметра (сокращенно смоченным периметром) называется та часть периметра живого сечения, в пределах которой жидкость соприкасается с ограждающими ее стенками.

8. Какие гидравлические факторы учитываются с помощью гидравлического радиуса?

Гидравлический радиус позволяет косвенно учесть влияние формы и размеров живого сечения

9. Назовите единицу измерения кинематического коэффициента вязкости.

ν – кинематический коэффициент вязкости жидкости, м2/с.

10. Для чего измеряется температура жидкости при проведении лабораторной работы №5?

11. От чего зависит коэффициент вязкости жидкости?

12. Как изменяется вязкость жидкости при повышении температуры?

С возрастанием температуры вязкость уменьшается

13. Как изменяется число Рейнольдса при понижении температуры?

С понижением температуры коэффициент уменьшается.

VI. Блок 6. Гидравлические сопротивления и потери напора. Лабораторные работы № 6 и 7

1. Каковы физические причины возникновения гидравлических сопротивлений?

Поток жидкости в трубопроводе затрачивает энергию на преодоление сил трения, которые возникают как в самой жид­кости, так и между жидкостью и стенками трубопровода. Силы трения, преодолеваемые потоком, называются гидрав­лическими сопротивлениями.

2. Какова физическая сущность понятия «потери напора»?

Поскольку удельная энергия жидкости, отнесенная к единице веса, именуется в гидравлике напором, затраты энергии на преодоление сил трения получили название потерь напора.

Полная потеря напора определяется суммированием по­терь на отдельных участках и местных сопротивлениях

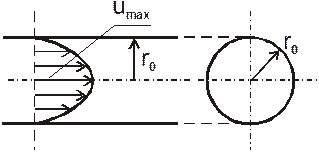
4. Нарисуйте эпюры распределения скоростей в живом сечении потока жидкости в напорной круглой трубе при ламинарном и турбулентном режимах

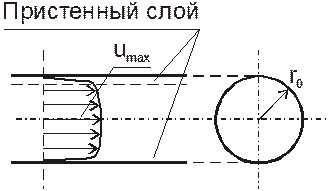
Турбулентный режим ламинарный режим

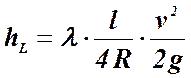
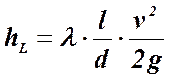
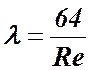
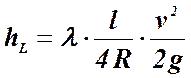
5. Для чего употребляются формулы . Поясните смысл величин, входящих в формулы

при ламинарном режиме

(4.5)

при гидр.режиме (4.6)

Присутствие в этой формуле гидравлического радиуса живого сечения потока () говорит о том, что потери напора зависят не только от размеров, но и от формы живого сечения потока.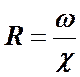

6. Нарисуйте и поясните схему строения пристенного слоя жидкости при турбулентном режиме

7. Как зависит толщина пристенного слоя от числа Рейнольдса?

Толщина пристенного слоя и градиенты скоростей в живом сечении зависят от числа Рейнольдса. Например, с увеличением числа Рейнольдса увеличивается турбулентность потока. Поэтому часть жидкости пристенного слоя вовлекается в перемешивание, и толщина пристенного слоя уменьшается с увеличением числа Рейнольдса. Соответственно, градиент скорости в пристенном слое увеличивается, а в турбулентном ядре потока уменьшается с увеличением числа Рейнольдса.

8. Что такое шероховатость?

Шероховатость это средняя высота неровностей на рассматриваемой поверхности.

9. Поясните понятия гидравлически гладкой и гидравлически шероховатой стенки

Если толщина ламинарного слоя больше шероховатости (δ > Δ), соответствующая поверхность называется гидравлически гладкой.

Если толщина ламинарного слоя меньше шероховатости (δ 3 4

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Коэффициент шези в чем измеряется

1. Методы применения законов гидравлики

1. Аналитический. Цель применения этого метода – устанавливать зависимость между кинематическими и динамическими характеристиками жидкости. С этой целью пользуются уравнениями механики; в итоге получают уравнения движения и равновесия жидкости.

Для упрощенного применения уравнений механики пользуются модельными жидкостями: например, сплошная жидкость.

По определению, ни один параметр этого континуума (сплошной жидкости) не может быть прерывным, в том числе его производное, причем в каждой точке, если нет особых условий.

Такая гипотеза позволяет установить картину механического движения и равновесия жидкости в каждой точке континуума пространства. Еще одним приемом, применяемом для облегчения решения теоретических задач, является решение задачи для одномерного случая со следующим обобщением для трехмерного. Дело в том, что для таких случаев не так трудно установить среднее значение исследуемого параметра. После этого можно получить другие уравнения гидравлики, наиболее часто применяемые.

Однако этот метод, как и теоретическая гидромеханика, суть которой составляет строго математический подход, не всегда приводит к необходимому теоретическому механизму решения проблемы, хотя и неплохо раскрывает ее общую природу проблемы.

2. Экспериментальный. Основным приемом, по этому методу, является использование моделей, согласно теории подобий: при этом полученные данные применяются в практических условиях и становится возможным уточнение аналитических результатов.

Наилучшим вариантом является сочетание двух вышеназванных методов.

Современную гидравлику трудно себе представить без применения современных средств проектирования: это высокоскоростные локальные сети, автоматизированное рабочее место конструктора и прочее.

Поэтому современную гидравлику нередко называют вычислительной гидравликой.

Поскольку газ – следующее агрегатное состояние вещества, то у этих форм вещества существует свойство, общее для обоих агрегатных состояний. Это свойство текучести.

Исходя из свойств текучести, рассмотрев жидкое и газообразное агрегатное состояние вещества, увидим, что жидкость – то состояние вещества, в котором его уже невозможно сжимать (или можно сжать бесконечно мало). Газ – такое состояние того же вещества, в котором его можно сжать, то есть газ можно назвать сжимаемой жидкостью, точно так же, как и жидкость – несжимаемым газом.

Другими словами, особых принципиальных различий, кроме сжимаемости, между газом и жидкостью не наблюдается.

Несжимаемую жидкость, равновесие и движение которой изучает гидравлика, называют также капельной жидкостью.

2. Основные свойства жидкости

Если рассмотреть произвольный объем жидкости W, то он имеет массу M.

Если жидкость однородна, то есть если во всех направлениях ее свойства одинаковы, то плотность будет равна

где M – масса жидкости.

Если требуется узнать r в каждой точке А объема W, то

где D – элементарность рассматриваемых характеристик в точке А.

Характеризуется коэффициентом объемного сжатия.

Из формулы видно, что речь идет о способности жидкостей уменьшать объем при единичном изменении давления: из-за уменьшения присутствует знак минус.

Суть явления втом, что слой с меньшей скоростью «тормозит» соседний. В итоге появляется особое состояние жидкости, из-за межмолекулярных связей у соседних слоев. Такое состояние называют вязкостью.

Отношение динамической вязкости к плотности жидкости называется кинематической вязкостью.

Поверхностное натяжение: из-за этого свойства жидкость стремится занимать наименьший объем, например, капли в шарообразных формах.

В заключение приведем краткий список свойств жидкостей, которые рассмотрены выше.

6. Температурное расширение.

7. Сопротивление растяжению.

8. Свойство растворять газы.

9. Поверхностное натяжение.

3. Силы, действующие в жидкости

Жидкости делятся на покоящиеся и движущиеся.

Здесь же рассмотрим силы, которые действуют на жидкость и вне ее в общем случае.

Сами эти силы можно разделить на две группы.

1. Силы массовые. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой ΔM = ρW действует сила ΔF, в зависимости от ее массы.

Пусть объем ΔW содержит в себе точку А. Тогда в точке А:

где FА – плотность силы в элементарном объеме.

Плотность массовой силы – векторная величина, отнесена к единичному объему ΔW; ее можно проецировать по осям координат и получить: Fx, Fy, Fz. То есть плотность массовой силы ведет себя, как массовая сила.

Примерами этих сил можно назвать силы тяжести, инерции (кориолисова и переносная силы инерции), электромагнитные силы.

Однако в гидравлике, кроме особых случаев, электромагнитные силы не рассматривают.

2. Поверхностные силы. Таковыми называют силы, которые действуют на элементарную поверхность Δw, которая может находиться как на поверхности, так и внутри жидкости; на поверхности, произвольно проведенной внутри жидкости.

Таковыми считают силы: силы давления которые составляют нормаль к поверхности; силы трения которые являются касательными к поверхности.

Если по аналогии (1) определить плотность этих сил, то:

нормальное напряжение в точке А:

касательное напряжение в точке А:

И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.

Источник

Формула Шези — формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока.

где V — средняя скорость потока, м/с;

C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления;

R — гидравлический радиус, м;

I — гидравлический уклон м/м.

где n — коэффициент шероховатости,характеризующий состояние поверхности русла, для случая канализационных труб принимается в диапазоне (0,012…0,015); для других случаев информация приведена в литературе [1]

C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления;

Формула Шези имеет то же предназначение, что и формула Дарси-Вейсбаха. Коэффициент потерь на трение <\displaystyle \lambda > связан с коэффициентом сопротивления C следующей зависимостью:

Наносы, — твёрдые частицы, переносимые водным или воздушным потоком

Влекомые наносы – это наносы, перемещающиеся речным потоком в природном слое и движущиеся скольжением, перекатыванием или сальтацией. Путем влечения по дну перемещаются наиболее крупные частицы наносов (песок, гравий, галька, валуны).

Чтобы оценить влияние различных факторов на движение влекомых наносов, в специальных разделах гидрологии рассматривают условия равновесия лежащей на дне реки частицы диаметром D. В направлении, параллельном дну, на частицу действуют две силы: сила лобового давления текущей воды, стремящаяся сдвинуть частицу и пропорциональная квадрату природной скорости течения и площади сечения частицы, и противоположно направленная сила трения, удерживающая частицу на дне.

Грядовый режим движения наносов наблюдается в условиях интенсивных вдольбереговых течений. Под их действием на береговых отмелях, сложенных песками, возникают гряды, близкие

по форме к обычным русловым. Чаще всего они располагаются между зоной разбивания волн и урезом. На узких отмелях 15-20m Кайраккумского водохранилища при скорости вдольберегового течения около 0,7-0,9 м/с в период исследований часто наблюдались трехмерные гряды руслового типа длиной 1,5-2,0 м и высотой 0,10-0,12 м На поверхности этих крупных гряд обычно перемещались более мелкие гряды с размерами примерно на порядок меньшими, чем у крупных гряд. Гряды больших и малых размеров обычно полностью исчезали по мере затухания шторма и вдольберегового течения.

Дата добавления: 2018-06-27 ; просмотров: 3607 ; Мы поможем в написании вашей работы!

Источник

Формулы для определения коэффициента Шези

Большинство формул для определения коэффициента Шези представляет собой эмпирические зависимости, действительные лишь для движения воды в определенном диапазоне скоростей и гидравлических радиусов.

1. Формула Н. Н.Павловского

(6.2)

где п — коэффициент шероховатости;

(6.3)

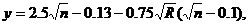
т. е. показатель у является функцией коэффициента шероховатости и гидравлического радиуса:

По указанию Н. Н. Павловского, приближенно можно принимать:

R 1m y=1.3 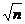. (6.5)

В приложении 10 приведены значения коэффициента Шези, подсчитанные но формуле Павловского.

2. При ориентировочных расчетах удобно пользоваться постоянным значением у. Обычно принимают у= =1/6, в результате чего получают формулу Маннинга:

(6.6)

Числовые значения коэффициента шероховатости n в формулах Павловского и Маннинга приведены в приложении 11.

3. В последние годы появились формулы для определения коэффициента Шези, действительные для всех однородных ньютоновских жидкостей и во всей области турбулентного движения.

Приводятся наиболее вероятные значения ε для средних условий, а в скобках указываются возможные пределы колебания.

Кним относятся формула А.Д.Альтшуля

(6.7)

v – кинематическая вязкость жидкости ;

g – ускорение свободного падения.

(6.8)

Значеня приведенной линейной шероховатости έ в формуле (6.8) даны в таблице 6.1

При значении критерия зоны турбулентности

(6.9)

вместо формулы (6.8) можно пользоваться более простой зависимостью:

(6.10)

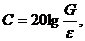
справедливой для вполне шероховатых русел. Формула (6.10) для большинства практически важных случаев дает результаты, близкие к тем, которые следуют из формулы Павловского.

при соблюдении условия

(6.11)

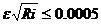
вместо формулы (6.8) можно пользоваться зависимостью

С=20 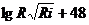, (6.12)

действительной для гидравлически гладких русел.

Формулу (6.8) можно приближенно представить в виде

(6.13)

где k и R- в мм; С— в м 1/2 /с.

Значение к_э и коэффициента n для различных поверхностей Таблица 6.3

Приводятся наиболее вероятные значения *. а в скобках — возможные пределы колебаний. для п приводятся возможные пределы колебаний.

Значения k (а также коэффициента n) для некоторых поверхностей приведены в табл. 6.3.

При отсутствии данных о величине k, для рассматриваемой поверхности можно пользоваться приближенной зависимостью

(6.14)

Для рек, формирующих русло в песчано-гравелистом ложе, коэффициент Шези можно находить и по формулам, не включающим коэффициентов шероховатости, например

С = 14,8/i 1/6 — 26. (6.15)

Эта формула действительна также для каналов, проходящих в естественных грунтах и несущих наносы.

Источник

Формула Шези

Формула Шези — формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером-гидравликом А. Шези (Antoine de Chézy, 1718–1798) в 1769 году. Применяется для расчётов потоков в речных руслах и канализационых системах.

,

де V — средняя скорость потока, м/с;

C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления; R — гидравлический радиус, м; I — гидравлический уклон м/м.

Формула Шези имеет то же предназначение, что и формула Дарси-Вейсбаха. Коэффициент потерь на трение связан с коэффициентом сопротивления C следующей зависимостью:

.

Коэффициент сопротивления C может быть определён по формуле Н. Н. Павловского:

где n — коэффициент шероховатости, характеризующий состояние поверхности русла, для случая канализационных труб принимается в диапазоне (0,012. 0,015); для других случаев nbsp;— информация приведена в литературе [1]

у — показатель степени, зависящий от величины коэффициента шероховатости и гидравлического радиуса:

Эта формула рекомендуется для значений R [2]

Источник