Хэш таблица что это
Хеш-таблица
| Определение: |
| Хеш-табли́ца (англ. hash-table) — структура данных, реализующая интерфейс ассоциативного массива. В отличие от деревьев поиска, реализующих тот же интерфейс, обеспечивают меньшее время отклика в среднем. Представляет собой эффективную структуру данных для реализации словарей, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу. |
Содержание
Введение [ править ]
Количество коллизий зависит от хеш-функции; чем лучше используемая хеш-функция, тем меньше вероятность их возникновения.
что в общем случае [math] \gt \dfrac<1><2>[/math]
Способ разрешения коллизий — важная составляющая любой хеш-таблицы.
Если мы поделим число хранимых элементов на размер массива [math]H[/math] (число возможных значений хеш-функции), то узнаем коэффициент заполнения хеш-таблицы (англ. load factor). От этого параметра зависит среднее время выполнения операций.
Хеширование [ править ]
Хеширование (англ. hashing) — класс методов поиска, идея которого состоит в вычислении хеш-кода, однозначно определяемого элементом с помощью хеш-функции, и использовании его, как основы для поиска (индексирование в памяти по хеш-коду выполняется за [math]O(1)[/math] ). В общем случае, однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов исходных данных, поэтому существуют элементы, имеющие одинаковые хеш-коды — так называемые коллизии, но если два элемента имеют разный хеш-код, то они гарантированно различаются. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций. Для того чтобы коллизии не замедляли работу с таблицей существуют методы для борьбы с ними.
Виды хеширования [ править ]
Статическое — фиксированное количество элементов. Один раз заполняем хеш-таблицу и осуществляем только проверку на наличие в ней нужных элементов,
Динамическое — добавляем, удаляем и смотрим на наличие нужных элементов.
Свойства хеш-таблицы [ править ]
Хеширование в современных языках программирования [ править ]
Почти во всех современных языках присутствуют классы, реализующие хеширование. Рассмотрим некоторые из них.
Хэш-таблицы
В этой статье вы познакомитесь с хэш-таблицами и увидите примеры их реализации в Cи, C++, Java и Python.
Хэш-таблица — это структура данных, в которой все элементы хранятся в виде пары ключ-значение, где:
Хэширование (хэш-функция)
В хэш-таблице обработка новых индексов производится при помощи ключей. А элементы, связанные с этим ключом, сохраняются в индексе. Этот процесс называется хэшированием.
Пусть k — ключ, а h(x) — хэш-функция.
Коллизии
Когда хэш-функция генерирует один индекс для нескольких ключей, возникает конфликт (неизвестно, какое значение нужно сохранить в этом индексе). Это называется коллизией хэш-таблицы.
Есть несколько методов борьбы с коллизиями:
1. Метод цепочек
Суть этого метода проста: если хэш-функция выделяет один индекс сразу двум элементам, то храниться они будут в одном и том же индексе, но уже с помощью двусвязного списка.
Псевдокод операций
2. Открытая адресация
Существует несколько видов открытой адресации:
a) Линейное зондирование
Линейное зондирование решает проблему коллизий с помощью проверки следующей ячейки.
Проблема линейного зондирования заключается в том, что заполняется кластер соседних ячеек. Это приводит к тому, что при вставке нового элемента в хэш-таблицу необходимо проводить полный обход кластера. В результате время выполнения операций с хэш-таблицами увеличивается.
b) Квадратичное зондирование
Работает оно так же, как и линейное — но есть отличие. Оно заключается в том, что расстояние между соседними ячейками больше (больше одного). Это возможно благодаря следующему отношению:
c) Двойное хэширование
h(k, i) = (h1(k) + ih2(k)) mod m
«Хорошие» хэш-функции
«Хорошие» хэш-функции не уберегут вас от коллизий, но, по крайней мере, сократят их количество.
Ниже мы рассмотрим различные методы определения «качества» хэш-функций.
1. Метод деления
Если k — ключ, а m — размер хэш-таблицы, то хэш-функция h() вычисляется следующим образом:
2. Метод умножения
3. Универсальное хеширование
В универсальном хешировании хеш-функция выбирается случайным образом и не зависит от ключей.
Что такое хеш-таблицы, и как они работают


Хеш-таблица (hash table) — это специальная структура данных для хранения пар ключей и их значений. По сути это ассоциативный массив, в котором ключ представлен в виде хеш-функции.
Пожалуй, главное свойство hash-таблиц — все три операции: вставка, поиск и удаление — в среднем выполняются за время O(1), среднее время поиска по ней также равно O(1) и O(n) в худшем случае.
Простое представление хеш-таблиц
Чтобы разобраться, что такое хеш-таблицы, представьте, что вас попросили создать библиотеку и заполнить ее книгами. Но вы не хотите заполнять шкафы в произвольном порядке.
Первое, что приходит в голову — разместить все книги в алфавитном порядке и записать все в некий справочник. В этом случае не придется искать нужную книгу по всей библиотеке, а только по справочнику.
А можно сделать еще удобнее. Если изначально отталкиваться от названия книги или имени автора, то лучше использовать некий алгоритм хеширования, который обрабатывает входящее значение и выдает номер шкафа и полки для нужной книги.
Зная этот алгоритм хэширования, вы быстро найдете нужную книгу по ее названию.
Учтите, что хеш-функция должна иметь следующие свойства:
Борьба с коллизиями (они же столкновения)
В идеальном случае, когда заранее известны все пары ключ-значение, достаточно легко реализовать идеальную хеш-таблицу, в которой время поиска будет постоянным (используется идеальная хеш-функция, которая определяет положения в таблице по целым значениям и без столкновений).
Но в большинстве случаев приходится бороться с коллизиями. Обычно применяются методы цепочек и открытой индексации.
Метод цепочек
Этот метод часто называют открытым хешированием. Его суть проста — элементы с одинаковым хешем попадают в одну ячейку в виде [https://ru.wikipedia.org/wiki/%D0%A1%D0%B2%D1%8F%D0%B7%D0%BD%D1%8B%D0%B9_%D1%81%D0%BF%D0%B8%D1%81%D0%BE%D0%BA связного списка].
То есть, если ячейка с хешем уже занята, но новый ключ отличается от уже имеющегося, то новый элемент вставляется в список в виде пары ключ-значение.
В C++ метод цепочек реализуется так:
Проверка ячейки и создание списка
Открытая индексация (или закрытое хеширование)
Второй распространенный метод — открытая индексация. Это значит, что пары ключ-значение хранятся непосредственно в хеш-таблице. А алгоритм вставки проверяет ячейки в некотором порядке, пока не будет найдена пустая ячейка. Порядок вычисляется на лету.
Самая простая в реализации последовательность проб — линейное пробирование (или линейное исследование). Здесь все просто — в случае коллизии, следующие ячейки проверяются линейно, пока не будет найдена пустая ячейка.
А алгоритм поиска ищет ячейки в том же порядке, что и при вставке, пока не найдет нужный элемент или пустую ячейку, которая говорит о том, что ключ отсутствует. В случае, если таблица будет заполнена, ее придется динамически расширять.
Метод линейного пробирования для открытой индексации на C++:
Проверка ячеек и вставка значения
Самое главное
Хеширование и хеш-таблицы применяются для более удобного хранения пар ключ-значение. Если нужна максимальная эффективность, то используйте хеш-таблицы со списками будет намного быстрее, чем обычная таблица.
Этот текст был написан несколько лет назад. С тех пор упомянутые здесь инструменты и софт могли получить обновления. Пожалуйста, проверяйте их актуальность.
Хеш-таблицы
Предисловие
Я много раз заглядывал на просторы интернета, нашел много интересных статей о хеш-таблицах, но вразумительного и полного описания того, как они реализованы, так и не нашел. В связи с этим мне просто нетерпелось написать пост на данную, столь интересную, тему.
Возможно, она не столь полезна для опытных программистов, но будет интересна для студентов технических ВУЗов и начинающих программистов-самоучек.
Мотивация использовать хеш-таблицы
Для наглядности рассмотрим стандартные контейнеры и асимптотику их наиболее часто используемых методов.
| Контейнер \ операция | insert | remove | find |
|---|---|---|---|
| Array | O(N) | O(N) | O(N) |
| List | O(1) | O(1) | O(N) |
| Sorted array | O(N) | O(N) | O(logN) |
| Бинарное дерево поиска | O(logN) | O(logN) | O(logN) |
| Хеш-таблица | O(1) | O(1) | O(1) |
Все данные при условии хорошо выполненных контейнерах, хорошо подобранных хеш-функциях
Из этой таблицы очень хорошо понятно, почему же стоит использовать хеш-таблицы. Но тогда возникает противоположный вопрос: почему же тогда ими не пользуются постоянно?
Ответ очень прост: как и всегда, невозможно получить все сразу, а именно: и скорость, и память. Хеш-таблицы тяжеловесные, и, хоть они и быстро отвечают на вопросы основных операций, пользоваться ими все время очень затратно.
Понятие хеш-таблицы
Хеш-таблица — это контейнер, который используют, если хотят быстро выполнять операции вставки/удаления/нахождения. В языке C++ хеш-таблицы скрываются под флагом unoredered_set и unordered_map. В Python вы можете использовать стандартную коллекцию set — это тоже хеш-таблица.
Реализация у нее, возможно, и не очевидная, но довольно простая, а главное — как же круто использовать хеш-таблицы, а для этого лучше научиться, как они устроены.
Для начала объяснение в нескольких словах. Мы определяем функцию хеширования, которая по каждому входящему элементу будет определять натуральное число. А уже дальше по этому натуральному числу мы будем класть элемент в (допустим) массив. Тогда имея такую функцию мы можем за O(1) обработать элемент.
Теперь стало понятно, почему же это именно хеш-таблица.
Проблема коллизии
Естественно, возникает вопрос, почему невозможно такое, что мы попадем дважды в одну ячейку массива, ведь представить функцию, которая ставит в сравнение каждому элементу совершенно различные натуральные числа просто невозможно. Именно так возникает проблема коллизии, или проблемы, когда хеш-функция выдает одинаковое натуральное число для разных элементов.
Существует несколько решений данной проблемы: метод цепочек и метод двойного хеширования. В данной статье я постараюсь рассказать о втором методе, как о более красивом и, возможно, более сложном.
Решения проблемы коллизии методом двойного хеширования
Мы будем (как несложно догадаться из названия) использовать две хеш-функции, возвращающие взаимопростые натуральные числа.
Одна хеш-функция (при входе g) будет возвращать натуральное число s, которое будет для нас начальным. То есть первое, что мы сделаем, попробуем поставить элемент g на позицию s в нашем массиве. Но что, если это место уже занято? Именно здесь нам пригодится вторая хеш-функция, которая будет возвращать t — шаг, с которым мы будем в дальнейшем искать место, куда бы поставить элемент g.
Мы будем рассматривать сначала элемент s, потом s + t, затем s + 2*t и т.д. Естественно, чтобы не выйти за границы массива, мы обязаны смотреть на номер элемента по модулю (остатку от деления на размер массива).
Наконец мы объяснили все самые важные моменты, можно перейти к непосредственному написанию кода, где уже можно будет рассмотреть все оставшиеся нюансы. Ну а строгое математическое доказательство корректности использования двойного хеширования можно найти тут.
Реализация хеш-таблицы
Для наглядности будем реализовывать хеш-таблицу, хранящую строки.
Начнем с определения самих хеш-функций, реализуем их методом Горнера. Важным параметром корректности хеш-функции является то, что возвращаемое значение должно быть взаимопросто с размером таблицы. Для уменьшения дублирования кода, будем использовать две структуры, ссылающиеся на реализацию самой хеш-функции.
Чтобы идти дальше, нам необходимо разобраться с проблемой: что же будет, если мы удалим элемент из таблицы? Так вот, его нужно пометить флагом deleted, но просто удалять его безвозвратно нельзя. Ведь если мы так сделаем, то при попытке найти элемент (значение хеш-функции которого совпадет с ее значением у нашего удаленного элемента) мы сразу наткнемся на пустую ячейку. А это значит, что такого элемента и не было никогда, хотя, он лежит, просто где-то дальше в массиве. Это основная сложность использования данного метода решения коллизий.
Помня о данной проблеме построим наш класс.
На данном этапе мы уже более-менее поняли, что у нас будет храниться в таблице. Переходим к реализации служебных методов.
Из необходимых методов осталось еще реализовать динамическое увеличение, расширение массива — метод Resize.
Увеличиваем размер мы стандартно вдвое.
Немаловажным является поддержание асимптотики O(1) стандартных операций. Но что же может повлиять на скорость работы? Наши удаленные элементы (deleted). Ведь, как мы помним, мы ничего не можем с ними сделать, но и окончательно обнулить их не можем. Так что они тянутся за нами огромным балластом. Для ускорения работы нашей хеш-таблицы воспользуемся рехешом (как мы помним, мы уже выделяли под это очень странные переменные).
Теперь воспользуемся ими, если процент реальных элементов массива стал меньше 50, мы производим Rehash, а именно делаем то же самое, что и при увеличении таблицы (resize), но не увеличиваем. Возможно, это звучит глуповато, но попробую сейчас объяснить. Мы вызовем наши хеш-функции от всех элементов, переместим их в новых массив. Но с deleted-элементами это не произойдет, мы не будем их перемещать, и они удалятся вместе со старой таблицей.
Но к чему слова, код все разъяснит:
Ну теперь мы уже точно на финальной, хоть и длинной, и полной колючих кустарников, прямой. Нам необходимо реализовать вставку (Add), удаление (Remove) и поиск (Find) элемента.
Начнем с самого простого — метод Find элемент по значению.
Далее мы реализуем удаление элемента — Remove. Как мы это делаем? Находим элемент (как в методе Find), а затем удаляем, то есть просто меняем значение state на false, но сам Node мы не удаляем.
Ну и последним мы реализуем метод Add. В нем есть несколько очень важных нюансов. Именно здесь мы будем проверять на необходимость рехеша.
Помимо этого в данном методе есть еще одна часть, поддерживающая правильную асимптотику. Это запоминание первого подходящего для вставки элемента (даже если он deleted). Именно туда мы вставим элемент, если в нашей хеш-таблицы нет такого же. Если ни одного deleted-элемента на нашем пути нет, мы создаем новый Node с нашим вставляемым значением.
Хеш-таблица.
Хеш-таблицей называется структура данных, предназначенная для реализации ассоциативного массива, такого в котором адресация реализуется посредством хеш-функции. Хеш-функция – это функция, преобразующая ключ key в некоторый индекс i равный h(key), где h(key) – хеш-код (хеш-сумма, хеш) key. Весь процесс получения индексов хеш-таблицы называется хешированием.
В общем случае хеш-таблица позволяет организовать массив, специфика которого проявляется в связанности индексов по отношению к хеш-функции; индексы могут быть не только целого типа данных (как это было в простых массивах), но и любого другого, для которого вычислимы хеш-коды. Данные, хранящиеся в виде такой структуры, удобны в обработке: хеш-таблица позволяет за минимальное время (O(1)) выполнять операции поиска, вставки и удаления элементов.
Предположим, имеется товарная накладная с информацией о датах и городах (когда и куда отправляются товары). Определенному товару соответствует его числовой код в диапазоне от 000000000 до 999999999:
Здесь ключами являются коды товаров, и как видно они, несмотря на отсутствие некоторых единиц продукции, заполняют весь диапазон. Такая организация данных не оптимальна, поскольку памяти для хранения списка выделяется больше чем нужно. Решением проблемы будет хеширование ключей списка.
И хорошо если известно у скольких элементов значения отсутствуют, тогда в качестве ключей можно использовать все те же коды, но когда это не так, то лучше в качестве них взять другие данные, например (в накладной) ими могут быть даты. У девятизначных кодов ключи имеют целочисленный тип данных, а у дат – символьные (строковые). Для хеширования понадобиться хеш-функция.
В качестве последней можно взять, например следующую:
Формальный параметр key это строка, состоящая из 10 символов, т. е. дата. Функция erase() удаляет из строки key 5 символов, после чего результат вида «месяц-число» присваивается переменной h, которая и будет индексом нового списка. Например, из ключа 2026-09-01, путем хеширования, получился хеш-код 09-01. Таким образом, размер накладной заметно сокращается, исчезают все пустые элементы.
Но в некоторых местах возможно возникновения проблем следующего типа: пусть имеется два ключа: 2017-06-06 и 2025-06-06, тогда результат работы функции в двух случаях будет 06-06, следовательно, разные значения в хеш-таблицы попадут под один и тот же индекс. Такая ситуация называется коллизией. Коллизий следует избегать, выбирая «хорошую» хеш-функцию, и используя один из методов разрешения конфликтов: открытое (метод цепочек) или закрытое (открытая адресация) хеширование.
Открытое хеширование.
Принцип организации хеш-таблицы методом открытого хеширования заключается в реализации логически связанных цепочек, начинающихся в ячейках хеш-таблицы. Под цепочками подразумеваются связанные списки, указатели на которые хранятся в ячейках хеш-таблицы. Каждый элемент связанного списка – блок данных, и если с некоторым указателем, хранящимся по адресу i, связаны n таких блоков (n>1), то это свидетельствует о том, что n ключей получили один и тот же хеш-код i, т. е. имеет место коллизия. Но метод открытого хеширования устраняет конфликт, поскольку данные хранятся не в самой таблице, а в связных списках, которые увеличиваются при возникновении конфликта.
Если в исходном массиве было всего N элементов (столько же будут содержать в совокупности и все списки), то средняя длина списков будет равна α=N/M, где M – число элементов хеш-таблицы, α – коэффициент заполнения хеш-таблицы. Предположив, например, что в списке на рисунке выше M=5 (заклеив 4-ую по счету строку), получим среднее число списков α=2.
Чтобы увеличить скорость работы операций поиска, вставки и удаления нужно, зная N, подобрать M примерно равное ему, т. к. тогда α будет равняться 1-ому или ≈1-ому, следовательно, можно рассчитывать на оптимальное время, в лучшем случае равное O(1). В худшем случае все N элементов окажутся в одном списке, и тогда, например, операция нахождения элемента (в худшем случае) потребует O(N) времени.
Закрытое хеширование.
Первый метод назывался открытым, потому что он позволял хранить сколь угодно много элементов, а при закрытом хешировании их количество ограниченно размером хеш-таблицы. В отличие от открытого хеширования закрытое не требует каких-либо дополнительных структур данных. В ячейках таблицы хранятся не указатели, а элементы исходного массива, доступ к каждому из которых осуществляется по хеш-коду ключа, при этом одна ячейка может содержать только один элемент.
Сам процесс заполнения хеш-таблицы с использованием алгоритма закрытого хеширования осуществляется следующим образом:
a) если h(keyi) – номер свободной ячейки таблицы T, то в последнюю записывается xi;
b) если h(keyi) – номер уже занятой ячейки таблицы T, то на занятость проверяется другая ячейка, если она свободна то xi заноситься в нее, иначе вновь проверяется другая ячейка, и так до тех пор, пока не найдется свободная или окажется, что все M ячеек таблицы заполнены.
Последовательность, в которой просматриваются ячейки хеш-таблицы, называется последовательностью проб. Последовательность проб задается специальной функцией, например интервал между просматриваемыми ячейками может вычисляться линейно, или увеличиваться на некоторое изменяющееся значение.
Рассмотрим метод закрытого хеширования на примере построения хеш-таблицы. Положим, имеется целочисленный массив A, состоящий из 9 элементов:
A[13]=8, A[56]=4, A[79]=1, A[37]=5, A[41]=2, A[76]=9, A[51]=3, A[93]=9, A[30]=1
Также есть хеш-таблица размера M=10, и хеш-функция h(key)=key % M (% – операция «остаток от деления»). Заполним хеш-таблицу элементами массив A: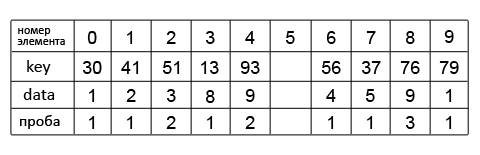
Используя формулу линейного пробирования (тип последовательности проб) hi(key)=(h(key) + i) % M (i – число проверок, после первой проверки i=0), продолжим поиск свободной ячейки. Применим функцию при i=1: h1(76)=7; убедившись, что ячейка 7 занята, продолжаем поиск, увеличив i на 1: h2(76)=8. Ячейка 8 свободна, помещаем в нее элемент. Этот же метод используем и для всех остальных элементов.


