что такое звенья ломаной 1 класс линии в математике
Ломаная линия
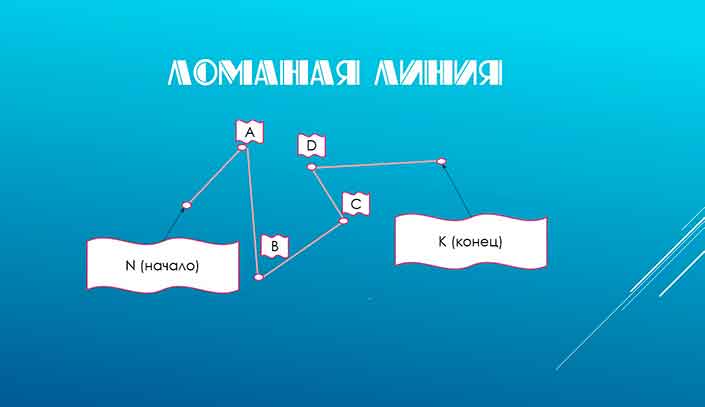
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
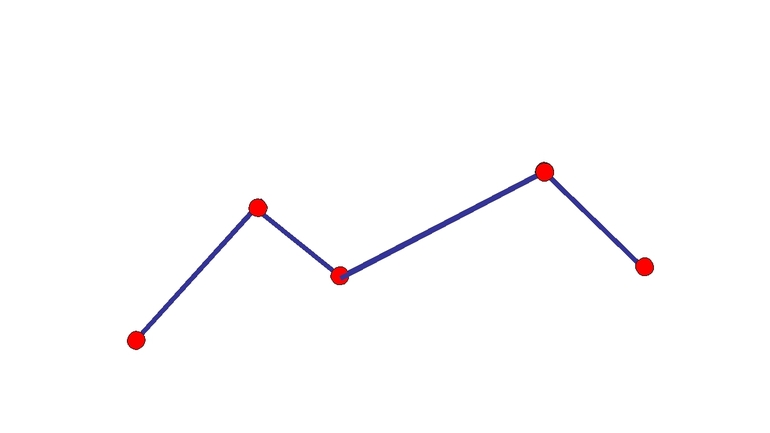
Построим ломаную из четырёх отрезков:
Замкнутая и незамкнутая ломаная
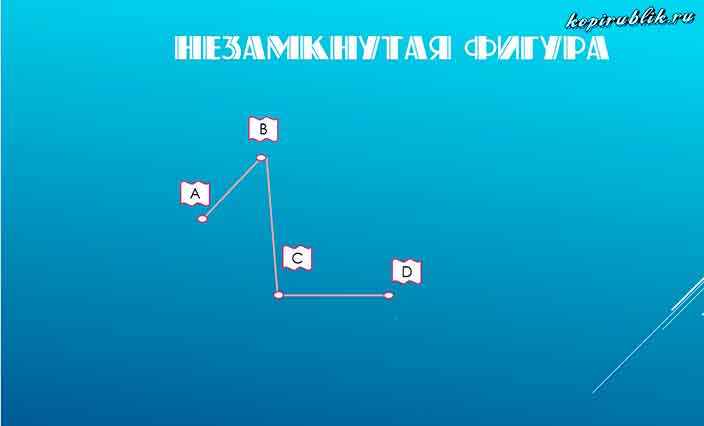
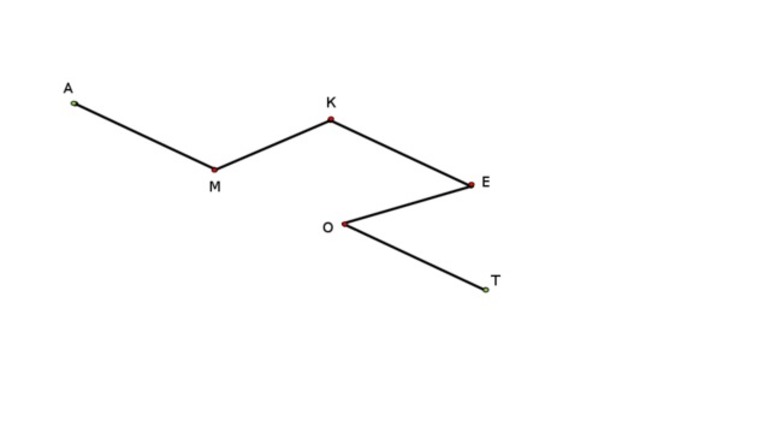
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
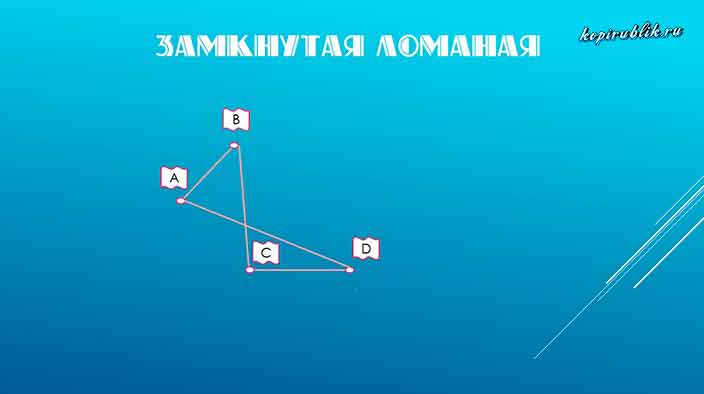
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
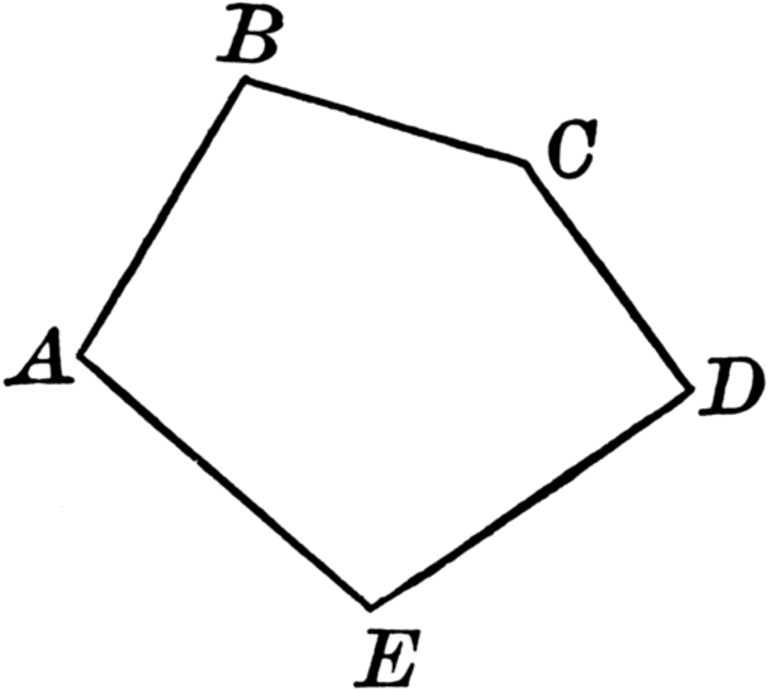
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Урок математики в 1-м классе. Тема: «Ломаная линия»
Продолжительность урока: 35 минут
Тип урока: Изучение и первичное закрепление нового материала.
Цель: Познакомить с ломаной линией и ее компонентами.
Задачи урока:
Ведущий вид деятельности: продуктивный, творческий, проблемный
Методы работы: объяснительно-иллюстративные, частично-поисковые, словесные, наглядные, практические.
Функция учителя: организатор сотрудничества; консультант, управляющий поисковой работой.
Педагогические технологии:
— педагогика сотрудничества (учебный диалог);
Список использованной литературы.
2. Истомина Н.Б. Рабочая тетрадь к учебнику «Математика» для 1 класса
3. Методические рекомендации к учебнику «Математика» 1 класс, под ред. Н.Б.Истоминой.- Смоленск: «Ассоциация ХХI век». 2006 год.
Ход урока
1. Оргмомент
Слайд 1. Звучит голос И.Левитана с сообщением о первом полёте человека в космос.
Учитель: Дети, 2011 год объявлен в нашей стране годом Российской космонавтики. А кто из вас интересуется космосом? Кто хочет полететь в космос? Сегодня представляется такая возможность для всего класса. Мы совершим учебный полёт. Чтобы не совершать ошибок во время полёта, нужно подготовиться, восстановить некоторые знания. Как вы думаете, что нам необходимо вспомнить?
Дети: Повторить числа, сложение и вычитание.
Учитель: Я соглашусь с вами, дети. Добавлю: нужно знать пройденные геометрические фигуры.
2. Актуализация прежних знаний
Учитель: На ваших столах лежат «Учебные маршрутные листы». Все результаты работы на уроке будем заносить на эти листы.
Итак, первое задание: «математический диктант». Прослушайте условие, высчитайте в уме, запишите только ответ.
Из 9 планет солнечной системы только две имеют женские имена. А сколько мужских имён в названиях планет солнечной системы? (7)
У созвездии «Большая медведица» 7 ярких звёзд. А в созвездии «Кассиопея» 5 ярких звёзд. На сколько больше ярких звёзд в созвездии Большая медведица? (2)
На мой вопрос в начале урока: «Кто мечтает полететь в космос?» ответили «да» 3 девочки и 7 мальчиков. Сколько всего ребят нашего класса хотят слетать в космос? (10)
Почему вторая фигура называется треугольником? (имеет три вершины и три стороны)
Учитель: В «Учебном маршрутном листе» найдите красную точку и постройте луч. Какой инструмент необходим? (Линейка)
Соедините две синие точки. Какая фигура у вас получилась? (Отрезок)
Через жёлтую точку проведите прямую линию. Можете провести ещё одну? А ещё? (Да!)
Верно, через одну единственную точку можно провести бесчисленное количество прямых линий.
3. Физкультминутка (Ребята выполняют упражнения, стоя у парт)
Раз, два!
Скорость света!
Три, четыре!
Мы летим!
На далёкие планеты
Поскорей попасть хотим!
Чтоб водить корабли,
Чтобы в небо взлететь,
Надо многое знать.
Надо много уметь!
И при этом, и при этом
Вы заметьте-ка,
Очень важная наука
Ма-те-ма-ти-ка!
4. Введение нового материала
Сегодня мы продолжаем путешествие в страну Геометрию.
Посмотрите, что у меня в руках? (Вермишель спагетти)
Какую геометрическую фигуру она вам напоминает? (Прямую линию)
Возьмите в руки спагетти, которые раздал вам дежурный. Переломите в середине, а затем каждую часть ещё раз переломите пополам.
Какие геометрические фигуры вам напоминают? (Отрезки, их получилось 4)
Соедините их кусочками пластилина между собой. Можно ли теперь назвать полученную фигуру прямой линией? (Нет)
Как бы вы назвали такую геометрическую фигуру? (Поломанная линия)
Я должна немного поправить вас, она называется «ломаная» линия.
Посмотрите, из чего состоит ломаная линия? (Из отрезков)
Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого. Место, где соединяются два звена, называется вершиной.
Сколько вершин у данной ломаной линии? (Три)
Кроме того, у ломаной линии есть 2 конца.
6. Первичное закрепление
Учитель: Дети, давайте вспомним ещё раз, какими бывают кривые линии? (Замкнутыми и незамкнутыми)
А как вы думаете, ломаные линии могут быть замкнутыми и незамкнутыми?
Учитель открывает на доске таблицу № 1:
— Какие фигуры изображены в таблице? (ломаные линии)
— У какой ломаной больше всего звеньев? (№ 4)
— У какой ломаной меньше всего звеньев? (№ 1)
— Какая ломаная имеет три вершины? (№ 2)
— Какая ломаная имеет пять вершин? (№ 4)
Учитель открывает на доске таблицу №2:
Учитель: Это тоже ломаные линии. Чем они отличаются от ломаных линий на первой таблице? (Все звенья соединены между собой)
— Назовите замкнутую ломаную линию, которая имеет меньше всего звеньев. (№1)
Верно, а может ли быть замкнутая линия из двух звеньев, подумайте. Давайте построим такую ломаную линию. (Нет, чтобы «замкнуть» линию нужно третье звено)
Учитель: Найдите и назовите на карте звёздного неба созвездия: незамкнутые ломаные линии и замкнутые.
Учитель: Если вашу «ломаную линию из спагетти» лежащую на парте, перевернуть, то будет напоминать созвездие «Кассиопею». Она была названа в честь царицы, которую заколдовала коварная колдунья.
7. Физкультминутка.
Для глаз. Дети следят за движением Колобка на Слайде№4
Задание на внимание
На несколько секунд я покажу вам одну фигуру. Вы должны запомнить её и выложить из счётных палочек точно такую.
Теперь поработайте в парах. Проверьте внимание своего одноклассника.
Какая фигура у вас получилась?
Что вы ещё скажете о ней? Можно ли её назвать ломаной линией?
Можно ли назвать её замкнутой? (незамкнутой?) Почему?
8. Подведение итога урока
С какой геометрической фигурой познакомились? (Ломаной линией)
Из каких элементов состоит ломаная линия? (Из звеньев и вершин)
Какие бывают ломаные линии? (Замкнутые и незамкнутые)
Переверните «Учебный маршрутный лист». Обведите цветным карандашом только ломаные линии, замкнутые и незамкнутые:
Какую линию описал корабль Ю.Гагарина за 108 минут вокруг Земли? (незамкнутую кривую линию)
В правом нижнем уголке «Учебного маршрутного листа» вам «улыбается» звёздочка. Какую геометрическую фигуру она напоминает? (Замкнутую ломаную линию) Определите количество вершин? Звеньев? Есть ли концы?
Самооценка работы учащихся на уроке:
Ломаная линия — что это такое простыми словами
Ломаная линия — определение
Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.
Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.
Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.
Таким образом, фигура в обязательном порядке отвечает нескольким признакам:
Обозначение ломаной линии
Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.
Из чего состоит ломаная линия
Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.
Признак замкнутости ломаной линии
Классификация ломаных линий прежде всего осуществляется по свойству замыкания.
Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.
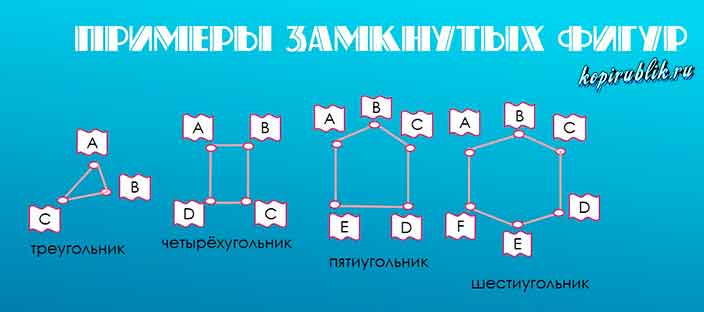
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:
Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.
Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».
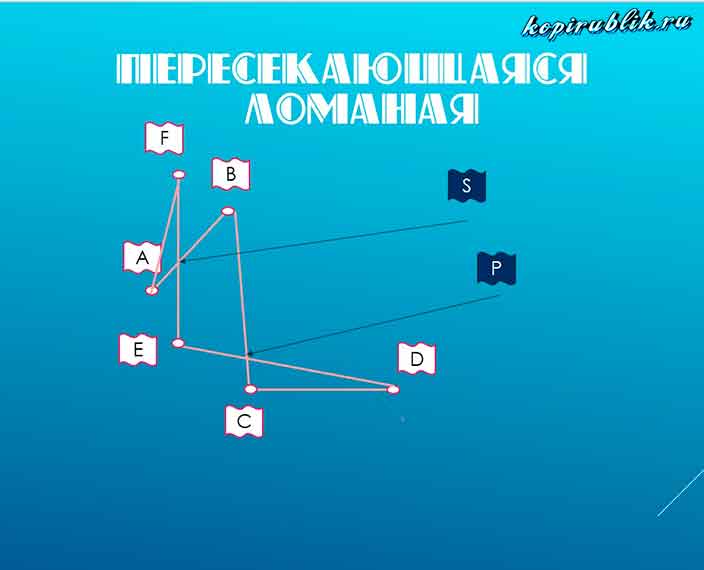
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.
На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.
Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:
Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.
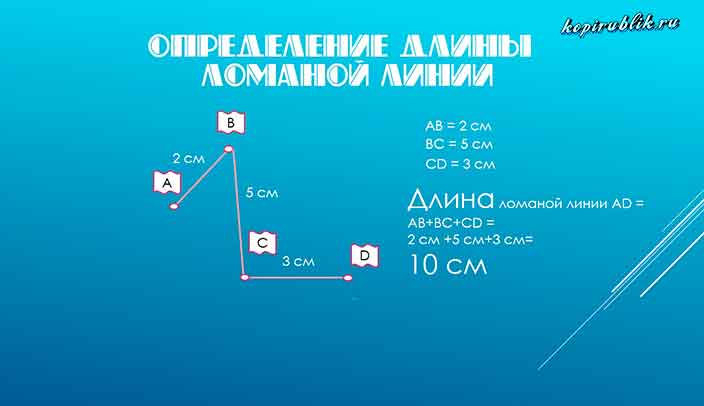
Как измерить длину ломаной линии
Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.
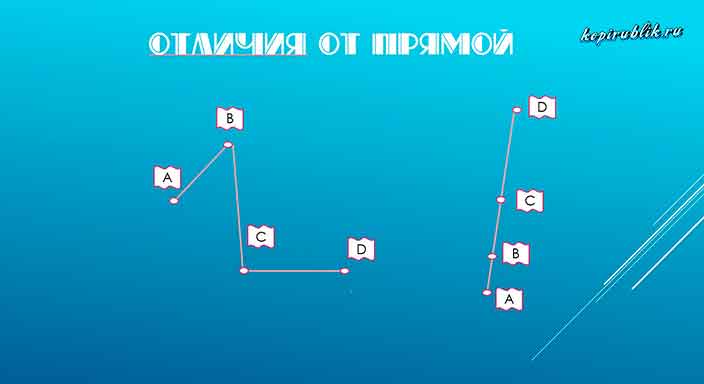
Чем ломаная линия отличается от прямой
При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.
Примеры ломаных линий в быту
В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.
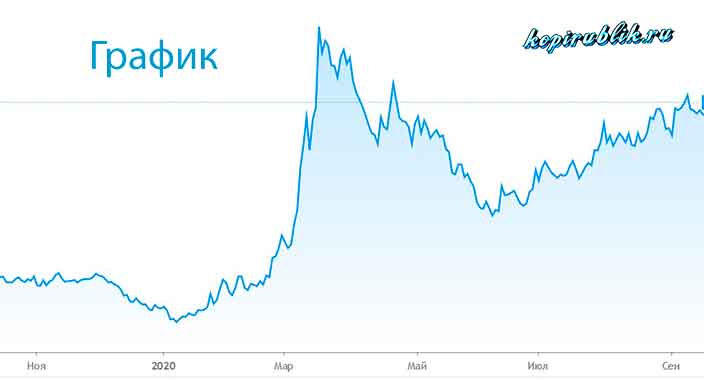
Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.
Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.
Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.
Урок математики по теме «Понятия «ломаная линия», «звено ломаной». Построение ломаных линий». 1-й класс
Класс: 1
Цель: путём наблюдения, сравнения познакомить детей с понятиями: ломаная линия, звенья и вершины ломаной линии.
Ведущий вид деятельности: продуктивный, творческий, проблемный
Методы работы: объяснительно – иллюстративные, частично – поисковые, словесные, наглядные, практические.
Функция учителя: организатор сотрудничества, консультант управляющий поисковой работой.
Вот звонок нам дал сигнал:
Поработать час настал.
Так что время не теряем,
И работать начинаем.
– Улыбнитесь друг другу, садитесь!
– Руки? – На месте!
– Ноги? – На месте!
– Локти? – У края!
– Спина? – Прямая!
II. Актуализация знаний учащихся.
— Сегодня мы с вами вновь отправляемся в удивительную страну, название этой страны узнаете, выполнив задания:
1. Счет от 1 до 10 в прямом и обратном порядке( хором, цепочкой)
2. Математический диктант
— Какое число следует за числом 8? ( 9 )
— Число 4 увеличить на 1.( 5 )
— Сколько хвостов у четырех щенят? ( 4 )
— Какое число стоит между числами 5 и 7? ( 6 )
— Какое число меньше 4 на 1? ( 3 )
— Какое число следует перед числом 2? ( 1 )
— Эта цифра из стихотворения С.Маршака похожа на кочергу. ( 7 )
— Число 3 уменьшить на 1. ( 2 )
— Это число соответствует количеству моих хлопков в ладоши. ( 8 )
Самопроверка по аналогу. Слайд №1
3. Расставление чисел в порядке возрастания, расшифровка названия страны :
9 5 4 6 3 1 7 2 8
я е м т о Г р е и
— Сегодня мы отправляемся в страну Геометрию. Что Вы знаете об этой стране?
— Чтобы запомнить все, что мы увидим в стране Геометрии, надо быть очень внимательным и наблюдательным. Поэтому сначала потренируем внимание и зрительную память. Запомните, что увидите.
Слайд № 3 ( геометрические фигуры)
— Что объединяет все рисунки? (Это геометрические фигуры)
— Какая фигура отличается от других? (шестиугольник)
— Каким по счету был 5-угольник? (второй )
— Назовите первую фигуру, третью фигуру (Треугольник, круг)
— Что вы знаете о луче?( Часть прямой линии, ограниченная с одной стороны).
III. Постановка цели урока.
На столе лежат конверты с заданием, на каждом листочке одна линия (ломаная, кривая, прямая, отрезок, луч, замкнутая кривая ).
— Какие варианты получились?
— Назовите известные вам линии. ( Кривая, прямая, отрезок, луч, замкнутая кривая.)
— Все линии назвали? ( Нет.)
— Почему? ( Не известно название одной линии.)
— А что бы вы хотели узнать про эту линию?
— Сегодня на уроке мы будем наблюдать за такими линиями, займёмся исследованием, совершим маленькие “открытия” и ответим на многие ваши вопросы.
IV. Открытие новых знаний
1. Знакомство с ломаной линией
— Посмотрите, что у меня в руках? (Вермишель спагетти)
— Какую геометрическую фигуру она вам напоминает? (Прямую линию)
— Возьмите в руки спагетти, которые раздал вам дежурный. Переломите в середине, а затем каждую часть ещё раз переломите пополам.
— Какие геометрические фигуры вам напоминают? (Отрезки, их получилось 4)
— Соедините их кусочками пластилина между собой. Можно ли теперь назвать полученную фигуру прямой линией? (Нет)
— Как бы вы назвали такую геометрическую фигуру? (Поломанная линия)
— Где можно узнать точное название линии и ее частей? ( в учебнике, в интернете)
2. Работа с учебником ( с. 4) Поиск новой информации.
Прочитайте правило, найдите ответы на вопросы:
— Как называется новая линия?
— Как называются части новой линии?
— Какое новое слово вы встретили?
Работа в паре. Ответы на вопросы.
3. Первичное закрепление.
— Посмотрите, из чего состоит ломаная линия?
— Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого.
— Что напоминает вам место, где соединяются два звена? (вершину горы)
Место, где соединяются два звена, называется вершиной.
Сколько вершин у данной ломаной линии? (Три)
Кроме того, у ломаной линии есть 2 конца.
4. Исследование ломаной линии путём практической работы.
— Попробуйте сконструировать ломаную линию
— Сколько звеньев у вашей ломаной? Покажите их.
— Сколько вершин получилось? Покажите их.
— Постройте свою ломаную линию.
— Проверьте работу в парах друг у друга и помогите, если у кого-то не получилось.
Вновь у нас физкультминутка, (Рывки руками перед грудью.) Наклонились, ну-ка, ну-ка! Голова устала тоже. (Наклоны вперед и назад.) Распрямились, потянулись, Так давайте ей поможем! А теперь назад прогнулись. Вправо-влево, раз и два. (Наклоны вправо и влево.) Думай, думай, голова. (Вращение головой.)
V. Упражнение в применении знаний.
(Отрезки можно начертить только по линейке. Ломаную линию так же).
— Как будем соединять точки? (Последовательно. Друг за другом. Работаем аккуратно и точно.
— Из чего состоит ломаная? (Ломаная линия состоит из отрезков.)
— Как называются эти отрезки?
— Сколько звеньев в нашей ломаной? ( 5 )
— Предположите, какое наименьшее количество звеньев может быть?
Вывод: наименьшее количество звеньев ломаной – 2.
— А 1 звено? (Это отрезок.)
— На что похожи места соединений? (Вершины гор. )
Вывод :Данные точки называются вершинами ломаной.
VI. Самостоятельная работа
— У каждого на столе лежат карточки. Прочитайте самостоятельно задание и выполните его. Если возникнут трудности- подайте сигнал. Кто выполнит –тоже зажигайте зелёный огонёк. (карточки разноуровневые)
Формирование умений соотносить цель и результат.
— На какие вопросы сегодня на уроке мы пытались ответить?
— Как называется новая линия?
— Как начертить ломаную линию?
— Как сконструировать ломаную линию?
— Где можно увидеть ломаную линию?
— Ответили на вопросы? Справились с работой?
— Выберите начало предложения и постарайтесь закончить его:
Прозвенел и смолк звонок,
Вот и кончился урок!
Краткое описание
Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.
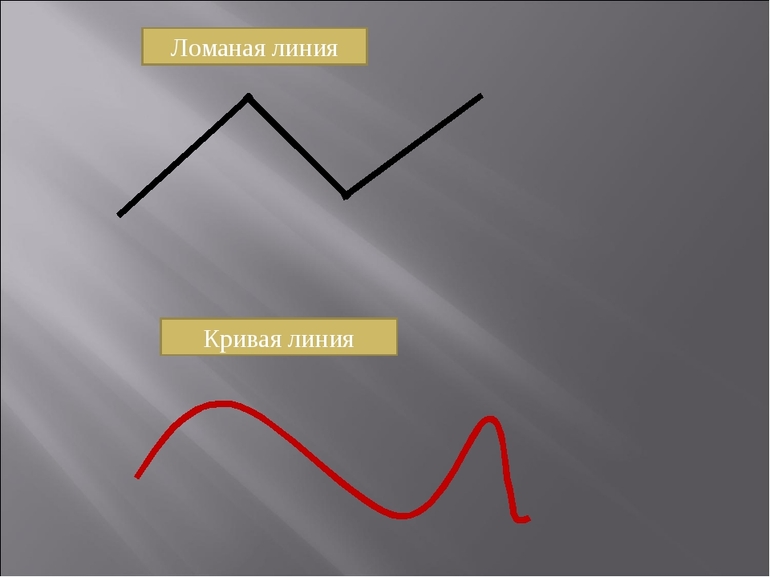
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.
В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.
Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.
Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.
Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.
Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.
Математическое определение
Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула <1, 2, n — 2>, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.
Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).
Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.
Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:
Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.
Основные разновидности ломаных
Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.
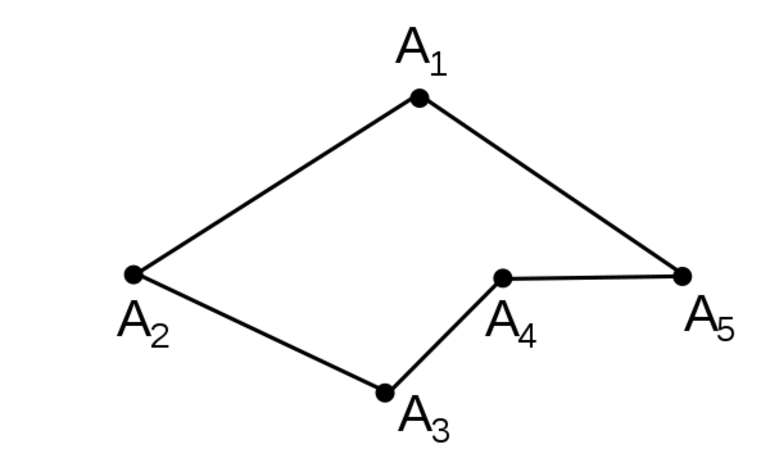
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.
Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.
Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:
Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).
Базовые понятия
Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.
Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.
Особенности построения многоугольников
В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.
Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.
Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.
Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:
Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.
Ключевые нюансы
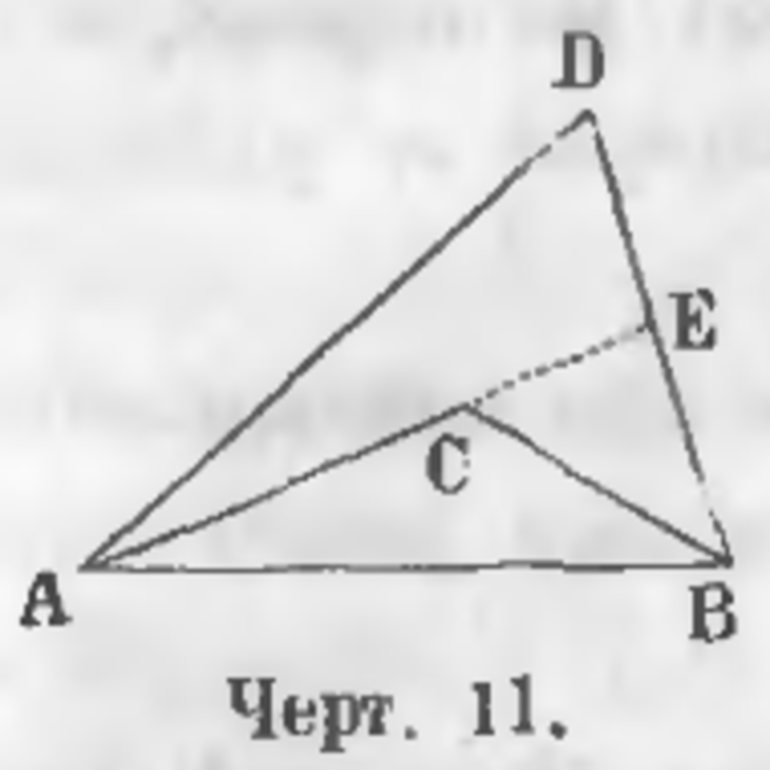
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.
Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:
Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.
Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.
Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.