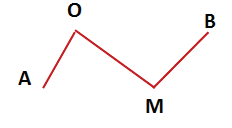
что такое звено в ломаной линии
Ломаная линия
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
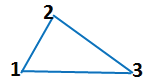
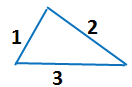
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
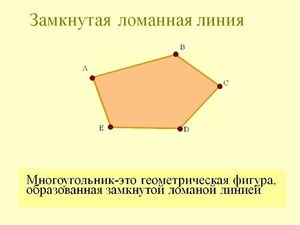
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
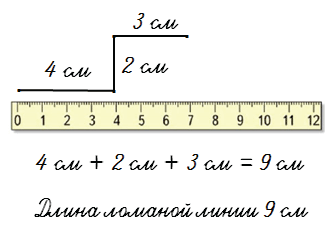
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Поделись с друзьями в социальных сетях:
Как выглядит замкнутая ломаная линия
Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.
Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:
Типы ломаных линий
Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.
Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.
Всего существует 4 типа подобных линий по своей структуре:
Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.
Особенности замкнутых линий
Рассмотрим подробнее составляющие части этой геометрической фигуры.
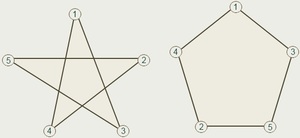
Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.
Многоугольник как разновидность замкнутой ломаной
Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.
Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.
Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.
Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.
У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.
Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.
Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.
Многоугольники
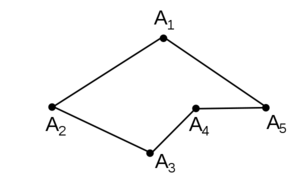
Ломаная — это геометрическая фигура, которая состоит из точек,
соединенных отрезками. Отрезки называются звеньями ломаной,
а точки называются вершинами ломаной. Сумма длин всех
звеньев называется длиной ломаной.
Замкнутая ломаная — это ломаная, у которой конец последнего
звена совпадает с началом первого звена.
Простая ломаная — это ломаная, у которой нет пересечений.
Многоугольник — это геометрическая фигура с множеством
углов и сторон, или по другому это простая замкнутая ломаная,
у которой соседние звенья не лежат на одной прямой.
Как и у любой другой геометрической фигуры, у многоугольника
есть стороны и углы. Звенья ломаной называют сторонами
многоугольника, а вершины ломаной называют углами
многоугольника. Периметр многоугольника равен сумме
длин всех сторон многоугольника, или по другому длине ломаной.
Соседние вершины многоугольника — это два угла
многоугольника,принадлежащие одной стороне.
Диагональ многоугольника — это отрезок, соединяющий
две любые не соседних угла.
Произвольный многоугольник разделяет плоскость на две части.
Одна из частей называется внутренней областью, а другая внешней
областью многоугольника. Углы, которые находятся во внутренней
области называются внутренними, соответственно углы, которые
находятся во внешней области называются внешними.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Урок математики по теме «Понятия «ломаная линия», «звено ломаной». Построение ломаных линий». 1-й класс
Класс: 1
Цель: путём наблюдения, сравнения познакомить детей с понятиями: ломаная линия, звенья и вершины ломаной линии.
Ведущий вид деятельности: продуктивный, творческий, проблемный
Методы работы: объяснительно – иллюстративные, частично – поисковые, словесные, наглядные, практические.
Функция учителя: организатор сотрудничества, консультант управляющий поисковой работой.
Вот звонок нам дал сигнал:
Поработать час настал.
Так что время не теряем,
И работать начинаем.
– Улыбнитесь друг другу, садитесь!
– Руки? – На месте!
– Ноги? – На месте!
– Локти? – У края!
– Спина? – Прямая!
II. Актуализация знаний учащихся.
— Сегодня мы с вами вновь отправляемся в удивительную страну, название этой страны узнаете, выполнив задания:
1. Счет от 1 до 10 в прямом и обратном порядке( хором, цепочкой)
2. Математический диктант
— Какое число следует за числом 8? ( 9 )
— Число 4 увеличить на 1.( 5 )
— Сколько хвостов у четырех щенят? ( 4 )
— Какое число стоит между числами 5 и 7? ( 6 )
— Какое число меньше 4 на 1? ( 3 )
— Какое число следует перед числом 2? ( 1 )
— Эта цифра из стихотворения С.Маршака похожа на кочергу. ( 7 )
— Число 3 уменьшить на 1. ( 2 )
— Это число соответствует количеству моих хлопков в ладоши. ( 8 )
Самопроверка по аналогу. Слайд №1
3. Расставление чисел в порядке возрастания, расшифровка названия страны :
9 5 4 6 3 1 7 2 8
я е м т о Г р е и
— Сегодня мы отправляемся в страну Геометрию. Что Вы знаете об этой стране?
— Чтобы запомнить все, что мы увидим в стране Геометрии, надо быть очень внимательным и наблюдательным. Поэтому сначала потренируем внимание и зрительную память. Запомните, что увидите.
Слайд № 3 ( геометрические фигуры)
— Что объединяет все рисунки? (Это геометрические фигуры)
— Какая фигура отличается от других? (шестиугольник)
— Каким по счету был 5-угольник? (второй )
— Назовите первую фигуру, третью фигуру (Треугольник, круг)
— Что вы знаете о луче?( Часть прямой линии, ограниченная с одной стороны).
III. Постановка цели урока.
На столе лежат конверты с заданием, на каждом листочке одна линия (ломаная, кривая, прямая, отрезок, луч, замкнутая кривая ).
— Какие варианты получились?
— Назовите известные вам линии. ( Кривая, прямая, отрезок, луч, замкнутая кривая.)
— Все линии назвали? ( Нет.)
— Почему? ( Не известно название одной линии.)
— А что бы вы хотели узнать про эту линию?
— Сегодня на уроке мы будем наблюдать за такими линиями, займёмся исследованием, совершим маленькие “открытия” и ответим на многие ваши вопросы.
IV. Открытие новых знаний
1. Знакомство с ломаной линией
— Посмотрите, что у меня в руках? (Вермишель спагетти)
— Какую геометрическую фигуру она вам напоминает? (Прямую линию)
— Возьмите в руки спагетти, которые раздал вам дежурный. Переломите в середине, а затем каждую часть ещё раз переломите пополам.
— Какие геометрические фигуры вам напоминают? (Отрезки, их получилось 4)
— Соедините их кусочками пластилина между собой. Можно ли теперь назвать полученную фигуру прямой линией? (Нет)
— Как бы вы назвали такую геометрическую фигуру? (Поломанная линия)
— Где можно узнать точное название линии и ее частей? ( в учебнике, в интернете)
2. Работа с учебником ( с. 4) Поиск новой информации.
Прочитайте правило, найдите ответы на вопросы:
— Как называется новая линия?
— Как называются части новой линии?
— Какое новое слово вы встретили?
Работа в паре. Ответы на вопросы.
3. Первичное закрепление.
— Посмотрите, из чего состоит ломаная линия?
— Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого.
— Что напоминает вам место, где соединяются два звена? (вершину горы)
Место, где соединяются два звена, называется вершиной.
Сколько вершин у данной ломаной линии? (Три)
Кроме того, у ломаной линии есть 2 конца.
4. Исследование ломаной линии путём практической работы.
— Попробуйте сконструировать ломаную линию
— Сколько звеньев у вашей ломаной? Покажите их.
— Сколько вершин получилось? Покажите их.
— Постройте свою ломаную линию.
— Проверьте работу в парах друг у друга и помогите, если у кого-то не получилось.
Вновь у нас физкультминутка, (Рывки руками перед грудью.) Наклонились, ну-ка, ну-ка! Голова устала тоже. (Наклоны вперед и назад.) Распрямились, потянулись, Так давайте ей поможем! А теперь назад прогнулись. Вправо-влево, раз и два. (Наклоны вправо и влево.) Думай, думай, голова. (Вращение головой.)
V. Упражнение в применении знаний.
(Отрезки можно начертить только по линейке. Ломаную линию так же).
— Как будем соединять точки? (Последовательно. Друг за другом. Работаем аккуратно и точно.
— Из чего состоит ломаная? (Ломаная линия состоит из отрезков.)
— Как называются эти отрезки?
— Сколько звеньев в нашей ломаной? ( 5 )
— Предположите, какое наименьшее количество звеньев может быть?
Вывод: наименьшее количество звеньев ломаной – 2.
— А 1 звено? (Это отрезок.)
— На что похожи места соединений? (Вершины гор. )
Вывод :Данные точки называются вершинами ломаной.
VI. Самостоятельная работа
— У каждого на столе лежат карточки. Прочитайте самостоятельно задание и выполните его. Если возникнут трудности- подайте сигнал. Кто выполнит –тоже зажигайте зелёный огонёк. (карточки разноуровневые)
Формирование умений соотносить цель и результат.
— На какие вопросы сегодня на уроке мы пытались ответить?
— Как называется новая линия?
— Как начертить ломаную линию?
— Как сконструировать ломаную линию?
— Где можно увидеть ломаную линию?
— Ответили на вопросы? Справились с работой?
— Выберите начало предложения и постарайтесь закончить его:
Прозвенел и смолк звонок,
Вот и кончился урок!