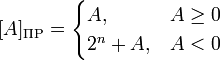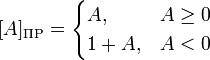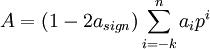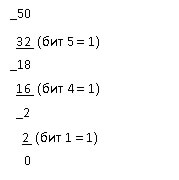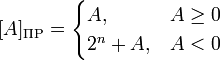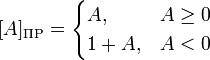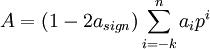что такое знаковый бит
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Знаковый бит
Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел.
Содержание
Представление числа в прямом коде
При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное. В остальных разрядах (которые называются цифровыми разрядами) записывается двоичное представление модуля числа.
Функция кодирования двоичных чисел (в том числе целых чисел и смешанных дробей) в прямом коде имеет вид:
где n — номер знакового разряда. В частности, при кодировании правильных двоичных дробей (то есть чисел − 1 ), n = 0 и функция кодирования принимает вид:
Величина числа A в прямом коде определяется по следующей формуле:
Как видно из последней формулы, знаковый разряд в прямом коде не имеет разрядного веса. При выполнении арифметических операций это приводит к необходимости отдельной обработки знакового разряда в прямом коде.
Примеры
Применение прямого кода
В информатике прямой код используется главным образом для записи неотрицательных целых чисел. Его легко получить из представления целого числа в любой другой системе счисления. Для этого достаточно перевести число в двоичную систему счисления, а затем заполнить нулями свободные слева разряды разрядной сетки машины.
Однако, у прямого кода есть два недостатка:
Выполнение арифметических операций над числами в прямом коде затруднено: например, даже для сложения чисел с разными знаками требуется кроме сумматора иметь специальный блок-«вычитатель», эффективно реализовать который, скорее всего, не представляется возможным. Кроме того, при выполнении арифметических операций требуется особо обрабатывать значащий разряд, так как он не имеет веса. Также требуется обработка «отрицательного нуля». Таким образом, выполнение арифметических операций над числами в прямом коде потребует сложной архитектуры центрального процессора и в общем является неэффективным.
Гораздо более удобным для выполнения арифметических операций является дополнительный код.
Диапазон
См. также
Полезное
Смотреть что такое «Знаковый бит» в других словарях:
знаковый бит — Бит, который показывает знак числа: положительное число (нуль) или отрицательное число (единица) (МСЭ Т T.800). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN sign bit … Справочник технического переводчика
A-закон — А закон алгоритм сжатия с потерей информации, применяется для сжатия звуковых данных. Реализации для 16 битных знаковых целых Принцип кодирования схож с кодированием чисел с плавающей запятой. Каждый семпл кодируется в 8 битное поле.… … Википедия
А-закон — А закон алгоритм сжатия с потерей информации, применяется для сжатия звуковых данных. Содержание 1 Описание реализации алгоритма для 16 битных знаковых целых 1.1 Шаг 1 1.2 Шаг 2 … Википедия
Битовое поле — Битовое поле в программировании число, занимающее некоторый набор битов, напрямую не адресуемый процессором. Например: при 8 битном байте первые два поля протокола IP версия и IHL будут битовыми полями. На машинах с 32 битным… … Википедия
Битовые поля — Битовое поле в программировании число, занимающее некоторый набор битов, напрямую не адресуемый процессором. Например: при 8 битном байте первые два поля протокола Обращение к битовым полям требует дополнительных команд процессора для… … Википедия
Запятая плавающая — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Машинный эпсилон — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление… … Википедия
Плавающая точка — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Что такое знаковый бит
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
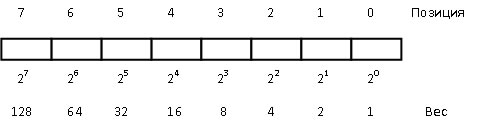
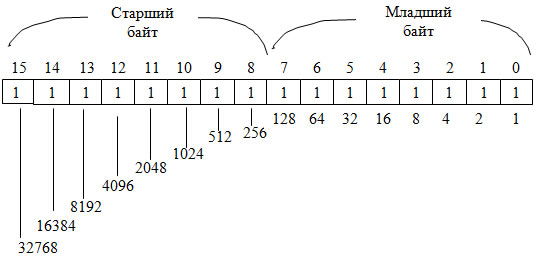
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.
Прямой код (представление числа)
Прямой код (представление числа)
Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи положительных чисел.
Содержание
Представление числа в прямом коде
При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное. В остальных разрядах (которые называются цифровыми разрядами) записывается двоичное представление модуля числа.
Функция кодирования двоичных чисел (в том числе целых чисел и смешанных дробей) в прямом коде имеет вид:
где n — номер знакового разряда. В частности, при кодировании правильных двоичных дробей (то есть чисел − 1 ), n = 0 и функция кодирования принимает вид:
Величина числа A в прямом коде определяется по следующей формуле:
Как видно из последней формулы, знаковый разряд в прямом коде не имеет разрядного веса. При выполнении арифметических операций это приводит к необходимости отдельной обработки знакового разряда в прямом коде.
Примеры
Применение прямого кода
В информатике прямой код используется главным образом для записи неотрицательных целых чисел. Его легко получить из представления целого числа в любой другой системе счисления. Для этого достаточно перевести число в двоичную систему счисления, а затем заполнить нулями свободные слева разряды разрядной сетки машины.
Однако, у прямого кода есть два недостатка:
Выполнение арифметических операций над числами в прямом коде затруднено: например, даже для сложения чисел с разными знаками требуется кроме сумматора иметь специальный блок-«вычитатель», сложность реализации которого, такая же, как и обычного сумматора. Кроме того, при выполнении арифметических операций требуется особо обрабатывать значащий разряд, так как он не имеет веса. Также требуется обработка «отрицательного нуля». Таким образом, выполнение арифметических операций над числами в прямом коде потребует сложной архитектуры центрального процессора и в общем является неэффективным.
Гораздо более удобным для выполнения арифметических операций является дополнительный код.
Диапазон
Материал из Википедии — свободной энциклопедии
В схемах обработки чисел с плавающей запятой, в отличие от схем с фиксированной запятой, во время представления чисел нужны два знаковых разряда: один — для представления знака мантиссы, другой — для представления знака порядке. Если используется модифицированный обратный и дополняющий код знак числа также изображается как двухразрядный код «00», в случае неотрицательных чисел, и как код «11» — в случае отрицательных чисел. Это даёт возможность легко определять ситуацию, при которой произошло переполнение разрядной сетки машины (признаком переполнения является наличие кода «01» или кода «10» в знаковом разряде).
Во время выполнения операций сложения (вычитания) знак результата получается автоматически, поскольку в операции участвуют не сами числа, а их коды (включая код знака). Во время выполнения операций умножения (деления) знак результата определяется суммированием кодов знакового разряда множимого и множителя (делимого и делителя) по mod 2.
Диапазон представления чисел со знаком
Изменение знака числа в разных кодах
В прямом коде знаковый бит обозначает знак числа, а цифровые биты содержат двоичные цифры числа. Для изменения знака числа в прямом коде достаточно изменить только знаковый бит.
В обратном коде знаковый бит обозначает знак числа, а цифровые биты содержат цифры числа для положительных чисел и инверсию цифр для отрицательных чисел. Для изменения знака числа нужно инвертировать все биты числа.
Расширение знака
Если необходимо привести число в дополнительном коде к более широкому формату, не меняя его числового значения (например, с одного до двух байтов), то дополнительные старшие биты должны быть заполнены копией знакового бита, этот процесс называется расширением знака [3] или размножением знака. Например, однобайтовое положительное двоичное число 00111010, расширенное до двух байтов, записывается в дополнительном коде как 00000000.00111010, а отрицательное число 11000110 как 11111111.11000110.
Процессоры семейства x86 имеют специальные команды расширения знака CBW (Convert Byte to Word), CWD и CWDE (Convert Word to Doubleword), CDQ (Convert Doubleword to Quadword)) и универсальную команду MOVSX (Move with Sign-Extension), предназначенные для автоматического увеличения формата числа.