что такое значимость результата
Статистическая значимость
Статистическая значимость часто применяется в маркетинге. С ее помощью определяют правильность выдвинутых предположений и вероятность их результатов. Она позволяет сделать выбор среди представленных теорий, что приводит к получению отличных результатов на практике.
Что такое статистическая значимость
Суть статистической значимости состоит в определении того, существует ли реальное основание в разнице между выбранными для исследования показателями, или это случайность? С данным понятием тесно связаны «нулевая» и «альтернативная» гипотезы.
Для лучшего понимания термина «статистическая значимость» необходимо понять, что такое «проверка гипотез». Эти два термина тесно взаимосвязаны.
Гипотеза иначе называется теорией. После окончания ее разработки требуется установить порядок по сбору достаточного количества доказательств этой теории и собрать их. Существует два типа гипотез: нулевая и альтернативная.
Нулевая гипотеза представляет собой теорию, которая гласит, что внесение коррективов ничего не поменяет, то есть сравниваемые объекты равнозначны в своих свойствах и нет смысла что-либо менять. Суть исследования заключается в опровержении гипотезы.
Альтернативная (исследовательская) гипотеза подразумевает сравнение, в результате которого один объект показывает себя эффективнее, чем другой.
Статистическая значимость как количественный показатель требует оценки. Оценка проходит поэтапно.
Постановка эксперимента
Все начинается с формулировки гипотезы. При этом должно быть выдвижение и нулевой, и альтернативной гипотезы. Придется сравнивать два набора данных для выяснения схожести и отличий. Эти утверждения требуют подтверждения с помощью экспериментальных данных.
Данный уровень представляет собой порог статистической значимости, который каждый устанавливает сам. Этот уровень носит название displaystyle \alpha >\alpha – уровня. Чаще всего, устанавливают значение в 0,05. Вероятность найти разницу составляет 5%. Чем выше уровень, тем достовернее результаты.
Когда нужна максимальная достоверность, стоит снизить значение с 0,05 до 0,01. Чаще всего, такие показатели применяют в производстве для выявления брака. Однако для большинства экспериментов достаточно значения в 0,05.
Решение об используемом критерии
После установки уровня требуется определить, какой критерий использовать: одно- или двусторонний. Здесь стоит опираться на t-критерии Стьюдента. Они показывают, насколько нормально распределены данные. Графически они представлены в виде колоколообразной кривой. Большее количество результатов расположено в середине.
Критерий Стьюдента позволяет математически проверить расположены ли данные в установленных пределах или же выпадают из нормального распределения.
Двусторонний критерий нужен, когда нет уверенности в том, что показатели находятся выше или ниже установленной нормы распределения.
Когда есть точная уверенность, в каком направлении может наблюдаться выход за пределы нормы, нужно использовать односторонний критерий.
Определение объема выборки
Здесь потребуется статистическая мощность. Она представляет собой вероятность, что при выбранном объеме будет получен ожидаемый результат. Распространенный порог — 80%. Для анализа можно использовать специальные онлайн-калькуляторы. Это позволит определить оптимальный объем выборки.
Часто проводят пробное исследование, которое позволяет получить данные для анализа и установить объем выборки. Когда такой возможности нет, стоит поискать в тематической литературе усредненные значения.
Вычисление стандартного отклонения
Стандартное отклонение показывает величину разброса данных. Оно позволяет сделать выбор о близости или отдаленности данных. Их вычисляют по следующей формуле: s = √∑((xi – µ)2/(N – 1)).
s — стандартное отклонение;
∑ указывает на необходимость суммировать полученные данные по выборке;
xi соответствует значению i, то есть отдельному полученному результату;
µ — это среднее значение для данной группы;
N — общее число данных в выборке.
Теперь потребуется отыскать среднее значение для каждой группы. Для этого суммируют средние значения каждой группы и делят на объем выборки.
Далее необходимо определить разницу (xi – µ). Для этого следует вычесть из найденной средней величины каждое полученное значение.
Теперь каждую полученную величину умножают на саму себя или возводят во вторую степень и суммируют величины. После этой операции не должно остаться отрицательных значений.
Следующий шаг — деление объема минус один. Делят полученную в предыдущем шаге сумму на величину, полученную от вычитания единицы. После этого извлекают квадратный корень из величины. Это и будет нужная величина стандартного отклонения.
Определение значимости
Для определения значимости потребуется взять две группы данных. Для последней вычисляют стандартное отклонение, после чего вычисляют дисперсию между обеими группами по формуле:
sd — дисперсия между двумя группами;
s1 — стандартное отклонение в группе 1, N1 — объем выборки в группе 1;
s2 — стандартное отклонение в группе 2, N2 — объем выборки в группе 2.
Необходимо определить t-оценку показателей для перевода полученных данных в стандартизированную форму, которая позволить провести сравнение с другими данными. Эта оценка делает возможным проверку t-критерия, а также выяснение величины отличия одной группы от другой. Для определения t-оценки применяют формулу: t = (µ1 – µ2)/sd:
µ1 — среднее значение для первой группы;
µ2 — среднее значение для второй группы;
sd — дисперсия между двумя выборками.
Совет: первым используют большее среднее значение, чтобы итоговая величина не была отрицательной.
Далее требуется определить степень свободы выборки. Для этого вычисляют объем: суммируют объемы двух выборок и вычитают 2. Полученная величина станет окончательной. Ее оценивают по таблице значений критерия Стьюдента (t-критерия). Таблица представлена ниже.
Пользоваться представленной таблицей просто: находите строку в соответствии с полученной степенью свободы и определяете соответствующее t-оценке Р-значение.
Например, при степени свободы 8 и t-оценке 2,61 Р-значение для одностороннего критерия попадает между 0,01 и 0,025. При выбранном показателе в 0,05 эти данные попадают в категорию «статистически значимые». Это помогает сделать выбор в пользу альтернативной гипотезы и отказаться от нулевой.
Заключение
Определение статистической значимости помогает решать маркетинговые задачи и минимизировать риски. Такие расчеты часто проводятся при A/B тестированиях и помогают узнать, как будет вести себя клиент в будущем, окупится ли товар и т.д.
Как посчитать статистическую значимость на пальцах
Бывает, нужно понять значима ли разница в аб эксперименте, но посчитать ее на специальном калькуляторе несподручно. Я разобрался и нашел способ считать статзначимость в прямом смысле на пальцах.
Подписывайтесь на канал, чтобы не пропустить клевые лайфхаки и истории про пет-проекты.
Итак, есть данные эксперимента по дням или по часам для контрольной и экспериментальной групп.
Ключевой вопрос: экспериментальная группа действительно идет выше, или это случайность?
Чтобы понять это, делаем следующее:
Выкидываем дни, когда данные в эксперименте и контроле совпали. Остается 12 дней, потому что на четвертый день количество продаж совпало.
Считаем сколько дней экспериментальная группа отклонялась в нетипичную сторону. В нашем случае было 2 дня — восьмой и девятый — когда эксперимент показал себя хуже контроля. В остальные дни он шел лучше.
Приятная особенность этого критерия — его можно применять к любым метрикам: и к конверсиям, и к уникам, и к просто абсолютным величинам, например деньгам. Вместо дней можно брать часы или недели.
Если критерий говорит, что результат значим — этому можно доверять. Если говорит, что не значим, но субъективно кажется, что должен быть значим, то воспользуйтесь другими более мощными критериями.
У критерия есть ограничение: если эксперимент длился 5 дней или меньше, то критерий всегда скажет, что результат не значим. Но стоит ли оценивать эксперименты по пяти дням — большой вопрос.
Я использовал симметричный критерий знаков — он универсальный и прост в расчете. Для него есть таблица значений: при каком количестве данных сколько можно допустить нетипичных отклонений. Я приблизил эту таблицу формулой (n-6)/3. На графике видно, что формула достаточно точно повторяет данные из таблицы. Формула иногда разрешает чуть меньшее количество отклонений — это значит, что мы получили чуть более осторожный критерий.
Практическая значимость результатов исследования
Практическая значимость – критерий, показывающий реальную пользу от применения результатов исследования в практической деятельности, их прикладную ценность. Обоснование практической значимости исследования дается в вводной части и подтверждается в заключении (или разделе обсуждения при его наличии).
Особенно важен данный пункт для статей, которые публикуются в изданиях, индексируемых в библиографических и реферативных базах данных. Научные исследования, имеющие конкретную практическую значимость, как правило, имеют больше шансов быть опубликованными в рейтинговых журналах.
Издательство СибАК представляет серию научных журналов для публикаций студентов, аспирантов, докторантов и научных сотрудников.
Правила и основы формулирования
Грамотная формулировка значимости проведенного исследования основывается на следующих принципах:
Авторам статей рекомендуется при подготовке формулировок точно придерживаться выбранной темы и поставленной цели исследования.
Ключевые постулаты
Практическая значимость подчеркивает прикладной характер полученных результатов, а также то, какие трансформации существующих процессов и явлений могут возникнуть в зонах их применимости. Для оценки практической ценности проведенного исследования важно проверить такие параметры, как:
При подведении итогов экспериментов необходимо различать научную новизну и научную значимость. Новизна подтверждается фактом представления публике ранее неизвестных открытий. Значимость подтверждает реальные сдвиги, которые произойдут при внедрении новых решений в ту или иную отрасль.
Пример формулировки
Примеры для дипломных работ или диссертационных исследований
«Практическая, подтвержденная в ходе апробации значимость данного исследования заключается в подготовке перечня разрешенных пищевых добавок, которые снижают риск асфиксии у предрасположенных к аллергии».
«Значение проведенного исследования на практике состоит в предложении опросного листа нового формата для кадровых агентств, который позволит повысить эффективность подбора персонала».
Примеры для курсовой
«Практическая значимость настоящего изыскания предполагает поэтапное внедрение бизнес-планов для парикмахерских».
«Использование предложенного варианта инновационных тренажеров детской моторики будет внедряться в детских дошкольных учреждениях».
«Разработанный алгоритм послужил основой технической схемы дизельного двигателя для трактора модельного ряда МТЗ».
«На практике доказано, что именно этот элемент системы тушения пожаров наилучшим образом отвечает за ее функциональность и безопасность применения».
Теоретические доводы служат базой любого изыскания, но без их применения в реальной жизни теряют значение. Правильно сформулированный итог проведенных экспериментов позволяет развиваться научным отраслям и внедрять разработки в повседневную жизнь. Аргументированное разъяснение практического подхода дает толчок к появлению инновационных методик.
Статистическая значимость в экспериментах и анализе данных
Что именно имеют в виду ученые и исследователи, когда заявляют, что что-то является или не является статистически значимым? Как установить статистическую значимость и как ее интерпретировать?
Добро пожаловать в 11-ю часть серии статей о статистике в электротехнике. До сих пор мы рассматривали как высокоуровневые определения, так и конкретные примеры статистических концепций, полезных для инженера-практика. Чтобы узнать больше о том, что мы рассмотрели, ознакомьтесь со статьями, перечисленными в меню с оглавлением выше, над статьей.
Статистическая значимость: туманная концепция?
Любой, кто обычно читает исследовательские статьи, часто сталкивается со «статистической значимостью», часто сопровождаемой загадочной ссылкой на p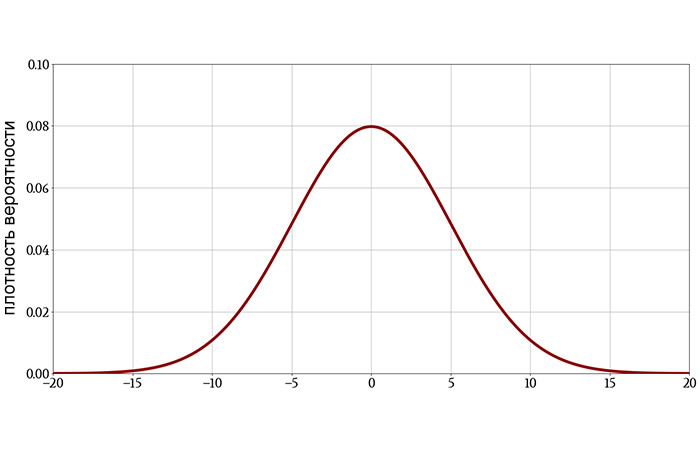 
Рисунок 1 – Если мы предполагаем, что нулевая гипотеза верна, мы часто будем использовать гауссову кривую в качестве функции плотности вероятности, с помощью которой мы решаем, является ли результат статистически значимым.
Порог вероятности
Статистическая значимость основана на вероятности получения результата при предположении, что нулевая гипотеза верна. Предположим, что в ходе нашего эксперимента мы получили число x (это может быть что угодно: артериальное давление, доход от продаж, средний балл теста).
Обращаясь к функции плотности вероятности, связанной с нулевой гипотезой, мы можем определить, будет ли вероятность получения x или какого-либо другого числа, которое более маловероятно, чем x, менее 5% (p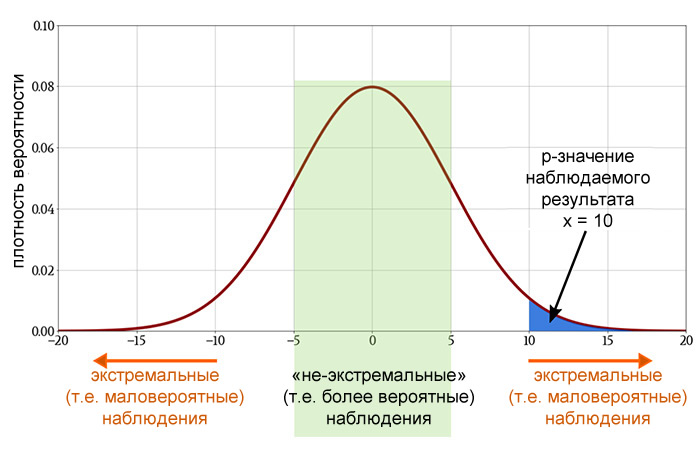 
Рисунок 2 – Гауссова кривая – это функция плотности вероятности, которая соответствует распределению значений, когда нулевая гипотеза верна. Мы вычисляем p-значение наблюдаемого результата путем интегрирования части этой функции плотности вероятности.
Если p-значение достаточно низкое, нет смысла продолжать предполагать, что между двумя переменными нет никакой связи. Таким образом, мы отвергаем нулевую гипотезу и утверждаем, что связь существует.
Интерпретация статистической значимости
Предыдущее объяснение описывает статистическую значимость способом, который я считаю наиболее простым и математически последовательным: если p-значение наблюдаемого результата меньше заранее определенного порога, который мы называем уровнем значимости, наблюдаемый результат очень маловероятен, если нулевая гипотеза верна. Поэтому, когда мы отвергаем нулевую гипотезу, это равносильно подтверждению того, что эксперимент обнаружил связь между интересующими переменными.
Это же общее сообщение можно передать другими способами, которые могут оказаться полезными:
Толкование слова «значимость»
Большая путаница в отношении статистической значимости возникает из-за использования слова «значимость», которое в данном контексте ограничивается конкретным статистическим использованием и не совпадает со словом «значимость» в обычном языке.
Статистически значимые результаты не обязательно являются важными или значимыми результатами. Статистическая значимость не означает практической значимости, а также отсутствие статистической значимости не означает, что экспериментальные результаты не имеют практической ценности.
Уровень значимости
Чтобы установить статистическую значимость, мы должны сравнить p-значение с уровнем значимости, обозначенным как ⍺. Уровни значимости в некоторой степени произвольны и выбираются в соответствии с условиями заданной области. Как было указано выше, часто используются ⍺ = 0,05 и ⍺ = 0,01, хотя в некоторых случаях выбирается более высокое или гораздо более низкое значение.
Заключение
Несмотря на возможное неправильное использование статистической значимости и доказательства широко распространенной неверной интерпретации, она остается важным методом в исследованиях и экспериментах. Мы продолжим изучение этой темы в следующей статье.
значимый результат
Как правило, некоторый
статистический показатель называют значимым, когда гипотеза о том, что он равен
нулю, не принимается. Так, говорят о значимом коэффициенте корреляции, значимом
коэффициенте регрессии и т.п.
Когда гипотезу о том, что значение
коэффициента равно некоторому значению, не принимают, также говорят о значимом
отличии коэффициента от этого значения.
Во всех этих случаях, говоря о
статистической значимости, имеют в виду, что результат выходит за тот диапазон
значений, в который укладываются случайные эффекты, когда нулевая гипотеза
верна. Поэтому иногда смысл термина расширяют и говорят о значимости, получив
результат статистической проверки, при котором нулевой
принимается. Если же нулевая гипотеза не отвергнута, то говорят, что результат
Пример. При проверке нулевой гипотезы H0() о среднем нормального распределения с известным
стандартным отклонением при альтернативе H1(
Смотреть что такое «значимый результат» в других словарях:
значимый результат — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN significance [significant] figure … Справочник технического переводчика
значимый результат (на выбранном уровне значимости a) — 2.84. значимый результат (на выбранном уровне значимости a) Результат статистической проверки, который приводит к отбрасыванию нулевой гипотезы, в противном случае результат незначим. Примечания 1. Когда результат проверки называют статистически… … Словарь-справочник терминов нормативно-технической документации
результат — 1. Итог какой либо деятельности, работы, занятия. О положительном, результате. Благонадежный (устар.), благоприятный, блестящий, блистательный, богатый, важный, верный, весомый, видимый, выдающийся, высокий, громадный, действительный, желанный,… … Словарь эпитетов
Значимый другой — человек, являющийся авторитетом для конкретного субъекта О. или деятельности. Впервые понятие З. д. ввел американский психолог Г. Салливен. В отеч. психологии наибольший вклад в изучение этого феномена сделан в работах В. А. Петровского,… … Психология общения. Энциклопедический словарь
ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения — Терминология ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа: 2.3. (генеральная) совокупность Множество всех рассматриваемых единиц. Примечание Для случайной величины… … Словарь-справочник терминов нормативно-технической документации
Клинические исследования — Клиническое исследование научное исследование с участием людей, которое проводится с целью оценки эффективности и безопасности нового лекарственного препарата или расширения показаний к применению уже известного лекарственного препарата.… … Википедия
Статистический вывод (statistical inference) — Процесс получения выводов о некой совокупности на основе случайно извлекаемых из нее выборок (в сущности, по ее частям или подмножествам) называется С. в. С. в. широко используется в психологии, поскольку редко удается обследовать полную… … Психологическая энциклопедия
Статистика в психологии (statistics in psychology) — Первое применение С. в психологии часто связывают с именем сэра Фрэнсиса Гальтона. В психологии под «статистикой» понимается применение количественных мер и методов для описания и анализа результатов психол. исслед. Психологии как науке С.… … Психологическая энциклопедия
Кластерный анализ — Для улучшения этой статьи по математике желательно?: Проставив сноски, внести более точные указания на источники. Исправить статью согласно стилистическим правилам Википедии. Переработать офо … Википедия
История «Новой хронологии» — Основная статья: Новая хронология (Фоменко) Содержание 1 Ранние попытки ревизии хронологии 2 В России 3 Идеи Н. А. Морозова … Википедия