что такое замыкание множества

Замкнутое множество

За́мкнутое мно́жество — подмножество пространства дополнение к которому открыто.

Содержание

Определение

Пусть дано топологическое пространство . Множество называется замкнутым относительно топологии , если существует открытое множество такое что .

Замыкание

Замыканием множества топологического пространства называют минимальное по включению замкнутое множество содержащее .

Замыкание множества обычно обозначается , или ; последнее обозначение используется если надо подчеркнуть что рассматривается как множество в пространстве .

Свойства

Примеры

См. также

Литература

Полезное

Смотреть что такое «Замкнутое множество» в других словарях:

замкнутое множество — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN closed set … Справочник технического переводчика

ЗАМКНУТОЕ МНОЖЕСТВО — в топологическом пространстве множество, содержащее все свои предельные точки. Таким образом, все точки дополнения к 3. м. внутренние, и потому 3. м. можно определить как дополнение к открытому. Понятие 3. м. лежит в основе определения топологич … Математическая энциклопедия

ОТНОСИТЕЛЬНО ОТКРЫТОЕ (ЗАМКНУТОЕ) МНОЖЕСТВО — множество, открытое (замкнутое) относительно нек рого множества Е, множество Мтопологич. пространства Xтакое, что (черта сверху означает операцию замыкания). Для того чтобы нек рое множество было открытым (замкнутым) относительно Е, необходимо и… … Математическая энциклопедия

ОТКРЫТО-ЗАМКНУТОЕ МНОЖЕСТВО — подмножество топологич. пространства, одновременно открытое и замкнутое в нем. Топологич. пространство Xнесвязно тогда и только тогда, когда в нем имеется отличное от Xи от О. з. м. Если семейство всех О. з. м. топологич. пространства является… … Математическая энциклопедия

Замкнутое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Замкнутое подмножество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия

Замкнутое пространство — Для одноимённого математического понятия, смотрите Замкнутое множество и Пространство (математика) Ливневая канализация … Википедия

Источник

Замкнутые и открытые множества

Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.

Приведем примеры замкнутых и открытых множеств. Всякий отрезок есть замкнутое множество, а всякий интервал — открытое множество. Несобственные полуинтервалы и замкнуты, а несобственные интервалы и открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек

Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.

1. Пересечение любого числа замкнутых множеств замкнуто.

2. Сумма любого числа открытых множеств есть открытое множество.

3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.

4. Если множество замкнуто, то его дополнение открыто и обратно.

Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.

В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).

Как видно из нижеследующего примера, замкнутые множества могут иметь весьма сложное строение.

Канторово совершенное множество

Рассмотрим некоторые свойства этого множества. Множество замкнуто, так как оно образуется путем удаления из прямой некоторого, множества непересекающихся интервалов. Множество не пусто; во всяком случае в нем содержатся концы всех выброшенных интервалов.

Можно показать, что множество имеет мощность континуума. В частности, отсюда следует, что канторово совершенное множество содержит, кроме концов смежных интервалов, еще и другие точки. Действительно, концы смежных интервалов образуют лишь счетное множество.

Разнообразные типы точечных множеств постоянно встречаются в самых различных разделах математики, и знание их свойств совершенно необходимо при исследовании многих математических проблем. Особенно большое значение имеет теория точечных множеств для математического анализа и топологии.

Исследования Н.Н. Лузина и его учеников показали, что имеется глубокая связь между дескриптивной теорией множеств и математической логикой. Трудности, возникающие при рассмотрении ряда задач дескриптивной теории множеств (в частности, задач об определении мощности тех или иных множеств), являются трудностями логической природы. Напротив, методы математической логики позволяют более глубоко проникнуть в некоторые вопросы дескриптивной теории множеств.

Источник

Теория функций действительного переменного/Множества в метрическом пространстве

В формулировках многих теорем анализа встречается понятие «окрестность точки». Наличие метрики позволяет ввести понятие окрестности в произвольном пространстве. Кроме того, в метрическом пространстве можно выделить подмножества, аналогичные шару в элементарной геометрии.

Содержание

Справедлива следующая теорема.

то есть диаметр ограниченного множества конечен. Необходимость доказана.

то есть является ограниченным. Теорема доказана.

Множество называется открытым, если любая точка этого множества принадлежит множеству вместе с некоторой своей окрестностью (то есть с открытым шаром c центром в этой точке).

Преобразование, ставящее в соответствие множеству его замыкание, называется операцией замыкания. Рассмотрим некоторые свойства операции замыкания.

Свойство 1. Множество целиком содержится в своём замыкании:

Данное свойство следует из того факта, что любая точка множества является его точкой прикосновения.

Свойство 2. Повторное применение операции замыкания не меняет результат:

а по аксиоме треугольника

Свойство 3. Замыкание подмножества есть подмножество замыкания содержащего его множества:

Свойство 4. Замыкание объединения множеств совпадает с объединением их замыканий:

Доказательство. По определению объединения множеств

следовательно, по свойству 3:

Докажем теперь обратное включение.

то есть для любой точки x ∈ M

Замечание. Иногда эту теорему берут за определение замкнутого множества, а тот факт, что замкнутое множество является дополнением открытого доказывают как теорему.

Из данной теоремы и свойств операции замыкания следует, что замыкание множества — это наименьшее замкнутое множество, содержащее данное.

Теорема 3. Пересечение любого числа и объединение любого конечного числа замкнутых множеств есть замкнутое множество.

Рассмотрим счётную систему множеств

В силу принципа двойственности справедлива следующая теорема.

Теорема 3а. Объединение любого числа и пересечение любого конечного числа открытых множеств суть открытые множества.

Отметим, что существуют множества не открытые и не замкнутые. Существуют и множества, являющиеся и открытыми, и замкнутыми: пустое множество и всё пространство.

Теорема 4. Всякая точка прикосновения множества есть либо предельная, либо изолированная точка этого множества.

Из этой теоремы следует, что замыкание множества M состоит, в общем случае, из точек трёх типов:

Таким образом, замыкание множества получается присоединением к нему всех его предельных точек.

Если в метрическом пространстве имеется счётное всюду плотное множество, то такое пространство называется сепарабельным.

Например, рациональные числа образуют счётное всюду плотное множество на числовой прямой, так как всякой вещественное число — это предел последовательности рациональных чисел.

Пространство изолированных точек является сепарабельным только если оно само счётно, так как в дискретной метрике замыкание любого множества совпадает с ним самим.

Упражнение 1. Доказать, что все точки открытого множества являются внутренними.

Источник

Замыкания множеств. Замкнутые и открытые множества.

Замечания. 1. Предельная точка может, как принадлежать, так и не принадлежать множеству. Например, 0 и 1 являются предельными точками множества (0,2), но первая ему не принадлежит, а вторая принадлежит.

Точка множества М может не являться его предельной точкой. В этом случае она называется изолированной точкой М. Например, 1  изолированная точка множества (1,0)<1>.

Если предельная точка а не принадлежит множеству М, то найдется последовательность точек х_n M, сходящаяся к а в этом метрическом пространстве. Для доказательства достаточно взять открытые шары в этой точке радиусов 1/n и выбрать из каждого шара точку, принадлежащую М. Верно и обратное, если для а есть такая последовательность, то точка является предельной.

ОПРЕДЕЛЕНИЕ 4. Замыканием множества М называется объединение М с множеством его предельных точек. Обозначение .

Отметим, что замыкание шара не обязано совпадать с замкнутым шаром того же радиуса. Например, в дискретном пространстве замыкание шара B(a,1) равно самому шару (состоит из одной точки a) в то время как замкнутый шар (a,1) совпадает со всем пространством.

Опишем некоторые свойства замыкания множеств.

М. Это следует непосредственно из определения замыкания.

Если М  N, то . Действительно, еслиa ,a М, то в любой окрестности a есть точки множества М. Они же являются точками N. Поэтому a. Для точек изМ это ясно по определению.

3. .

.

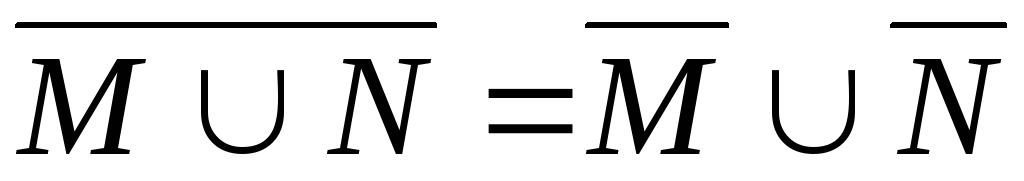
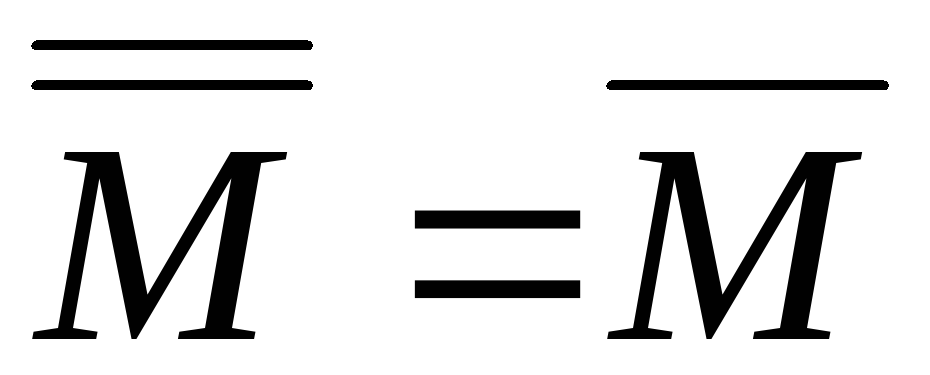
Замыкание пустого множества пустое. Это соглашение не следует из общего определения, но является естественным.

Множество M  X называется открытым, если замкнуто множество X\M.

Множество M  X называется всюду плотным в X, если ₌ X.

ОПРЕДЕЛЕНИЕ 6. Точка а называется внутренней точкой множества M, если B(a,r)M при некотором положительном r, т. е. внутренняя точка входит во множество вместе с некоторой окрестностью. Точка а называется внешней точкой множества M, если шар B(a,r)Х/M при некотором положительном r, т. е. внутренняя точка не входит во множество вместе с некоторой окрестностью. Точки, которые не являются ни внутренними, ни внешними точками множества M, называются граничными.

Таким образом, граничные точки характеризуются тем, что в каждой их окрестности есть точки как входящие, так и не входящие в M.

ПРЕДЛОЖЕНИЕ 4. Для того, чтобы множество являлось открытым, необходимо и достаточно, чтобы все его точки были внутренними.

Примерами замкнутых множеств на прямой являются [a,b], [a,). Открытых – (a,b), (a,). Множество [a,b) не открытое и не замкнутое (оно не содержит предельную точку b, а дополнительное множество не содержит предельную точку a). Все метрическое пространство Х и пустое множество  в силу соглашения 5 являются одновременно открытыми и замкнутыми. В дискретных метрических пространствах все подмножества одновременно открытые и замкнутые.

Из свойства 3 замыканий следует, что объединение двух (а тогда и любого конечного семейства) замкнутых множеств замкнуто. В то же время, объединение бесконечного семейства замкнутых множеств может и не быть замкнутым, например, 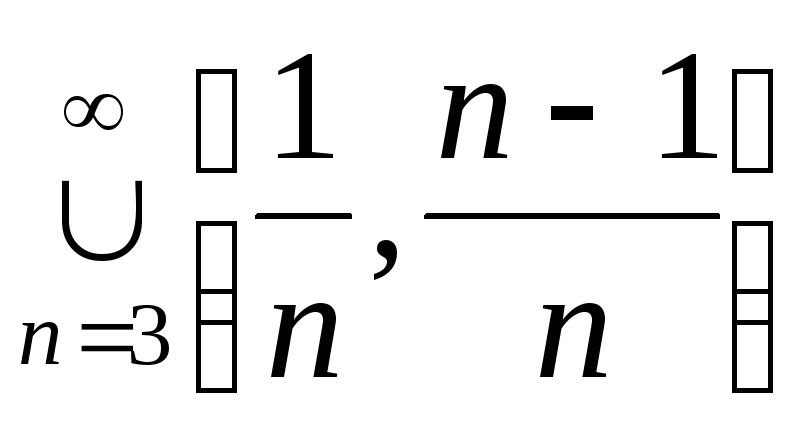= (0, 1).

Источник

Замыкание множества

Смотреть что такое «Замыкание множества» в других словарях:

ЗАМЫКАНИЕ МНОЖЕСТВА — в топологическом пространстве пересечение всех замкнутых множеств, содержащих данное множество. А. А. Мальцев … Математическая энциклопедия

Замыкание (геометрия) — У этого термина существуют и другие значения, см. Замыкание. Замыкание конструкция, дающая наименьшее замкнутое множество, содержащее данное множество топологического пространства. Замыкание множества обычно обозначается Содержание 1… … Википедия

Замыкание Клини — Звезда Клини (или замыкание Клини) в математической логике и информатике унарная операция над множеством строк либо символов. Замыкание Клини множества V обозначается V*. Широко применяется в регулярных выражениях, на примере которых было введено … Википедия

Замыкание (алгебра) — У этого термина существуют и другие значения, см. Замыкание. Замыкание в алгебре это замыкание относительно алгебраических операций. Определение Пусть подмножество некоторой алгебраической структуры (например, группы или кольца).… … Википедия

ЗАМЫКАНИЕ ВЫЧИСЛИТЕЛЬНОГО АЛГОРИТМА — система уравнений предельная при для системы частично разрешенных уравнений описывающих последовательные этапы вычислительного алгоритма решения уравнения (напр., сеточного уравнения, тогда h шаг сетки), аппроксимирующего при h >0 уравнение… … Математическая энциклопедия

РЕГУЛЯРНАЯ ФУНКЦИЯ МНОЖЕСТВА — аддитивная функция m, определенная на системе множеств топологич. пространства, полная вариация к рой удовлетворяет условию где внутренность множества замыкание множества F(E, G, F из области определения m). Ограниченная аддитивная Р. ф. м.,… … Математическая энциклопедия

Секвенциальное замыкание — Секвенциальная замкнутость более слабое свойство, чем топологическая замкнутость. Если множество топологически замкнуто, то оно и секвенциально замкнуто, но не наоборот. Содержание 1 Сходимость по топологии 2 Секвенциаль … Википедия

ЯДРО — множества, открытое ядро множества М совокупность всех внутренних точек М. Если А 1 В взаимно дополнительные множества топологич. пространства X, т. е. то где [А] замыкание множества А. М. И. Войцеховский … Математическая энциклопедия

Функциональная зависимость (программирование) — Функциональная зависимость концепция, лежащая в основе многих вопросов, связанных с реляционными базами данных, включая, в частности, их проектирование. Математически представляет бинарное отношение между множествами атрибутов данного… … Википедия

Источник