что такое замкнутая ломаная линия
Ломаная линия
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
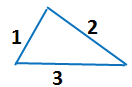
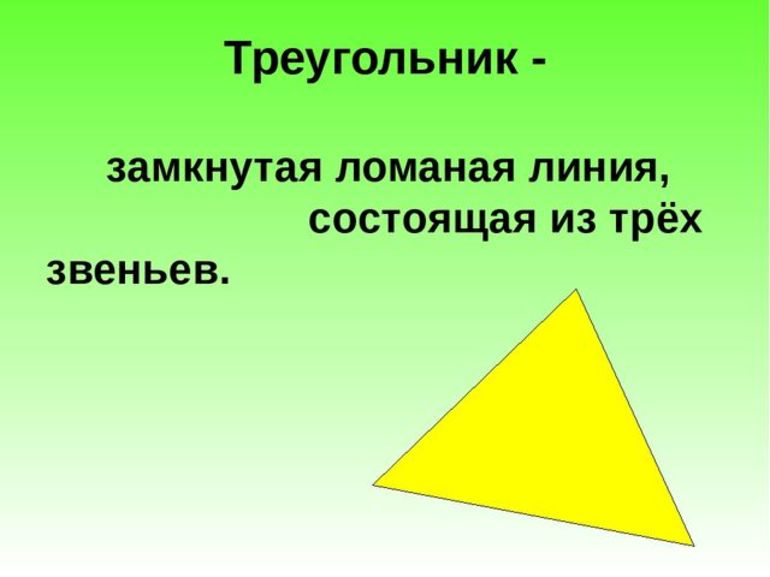
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
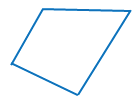
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
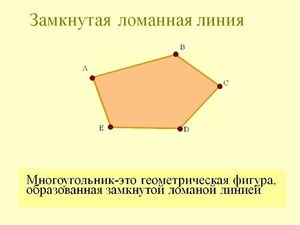
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Поделись с друзьями в социальных сетях:
Как выглядит замкнутая ломаная линия
Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.
Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:
Типы ломаных линий
Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.
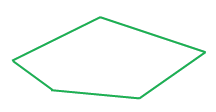
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.
Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.
Всего существует 4 типа подобных линий по своей структуре:
Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.
Особенности замкнутых линий
Рассмотрим подробнее составляющие части этой геометрической фигуры.
Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.
Многоугольник как разновидность замкнутой ломаной
Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.
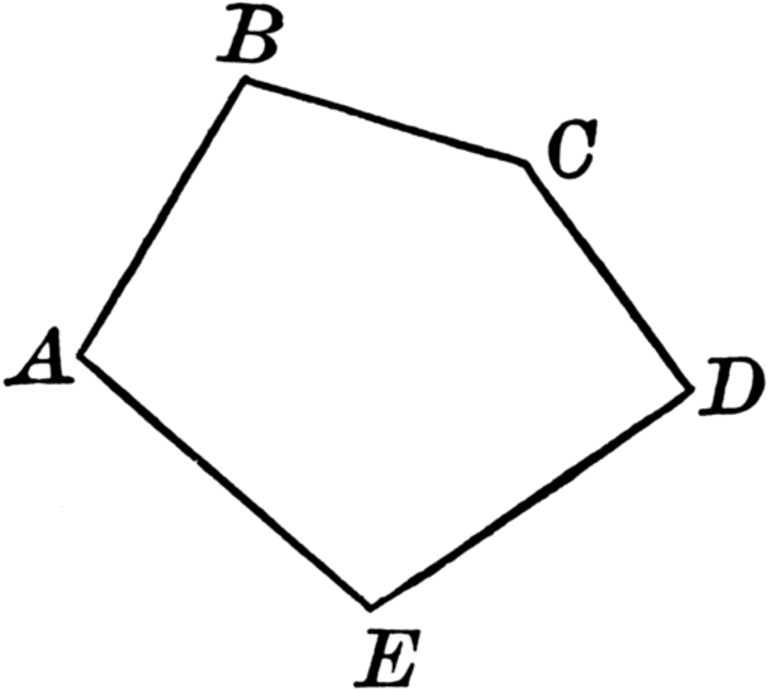
Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.
Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.
Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.
У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.
Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.
Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.
Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Замкнутая и незамкнутая ломаная
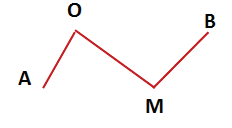
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
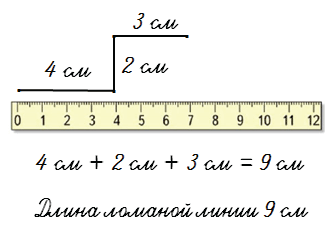
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Замкнутые самопересекающиеся ломаные
Александр Блинков, Александр Грибалко
«Квантик» №11, 2019
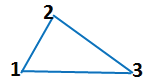
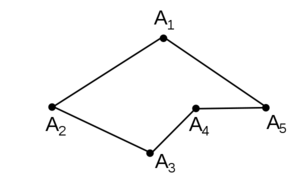
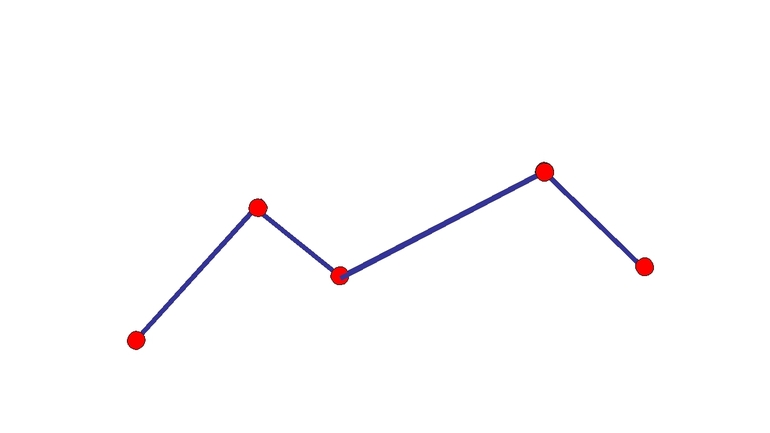
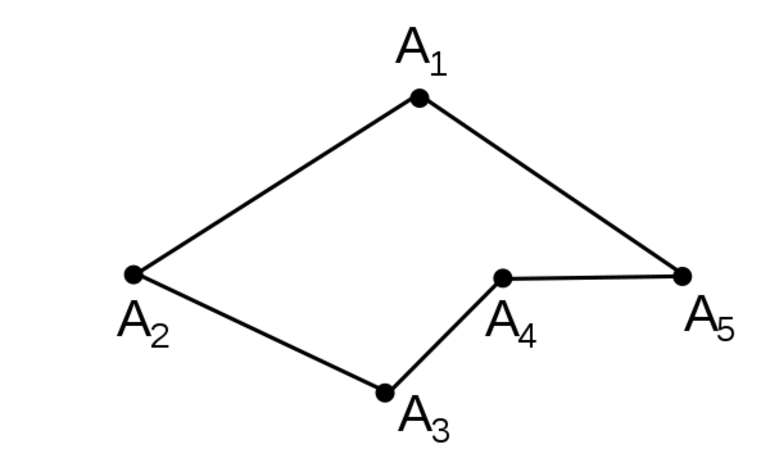
В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).
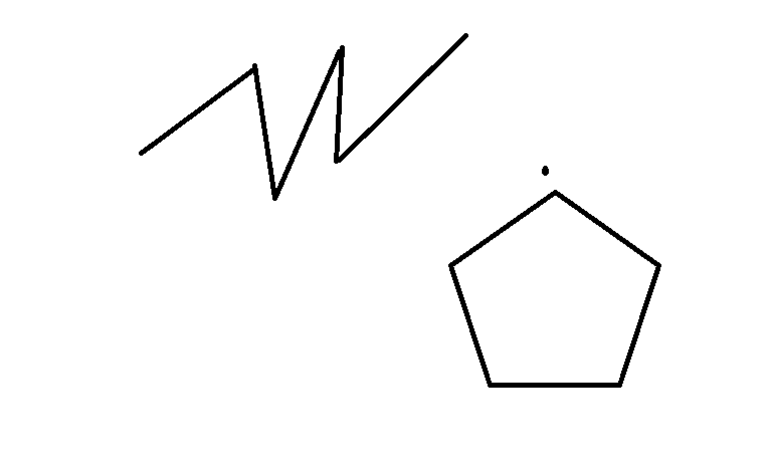
Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).
И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).
Нас будут интересовать замкнутые самопересекающиеся ломаные.
Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).
Задача 1
Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно два раза?
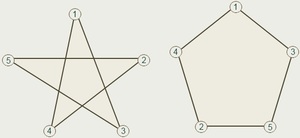
Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее. Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.
Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4, б — искомая ломаная с девятью звеньями.
Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.
Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.
Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.
Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.
Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).
Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.
Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?
Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.
Задача 2
Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно один раз?
Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.
Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).
Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.
Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение». Построим две ломаные из рис. 7, б с общей вершиной и «раздвоим» её (рис. 9, результат раздвоения — вершины с номерами 6 и 12). Понятно, что идея «раздвоения» вершин более универсальна. В том числе и потому, что позволяет комбинировать ломаные с разным количеством звеньев.
Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.
Упражнения и задачи для самостоятельного решения
1. Может ли прямая, не содержащая вершин замкнутой девятизвенной ломаной, пересечь каждое её звено?
2. (В. Произволов) Замкнутая ломаная такова, что каждые два её не соседних звена пересекаются. Докажите, что у этой ломаной нечётное количество звеньев.
3. Существует ли пятнадцатизвенная ломаная, пересекающая каждое своё звено ровно три раза?
4. Постройте восьмизвенную замкнутую ломаную, которая каждое своё звено пересекает один раз.
5. (Д. Калинин, вариация фольклора) Маша нарисовала замкнутую семизвенную ломаную. Для каждого звена она записала, со сколькими звеньями оно пересекается во внутренних точках. Могла ли она записать в каком-то порядке числа 1, 2, 3, 4, 3, 2, 1?
6. Какое наибольшее количество точек самопересечения может иметь замкнутая семизвенная ломаная?
7. (Н. Васильев) Рассматриваются всевозможные шестизвенные замкнутые ломаные, все вершины которых лежат на окружности.
Краткое описание
Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.
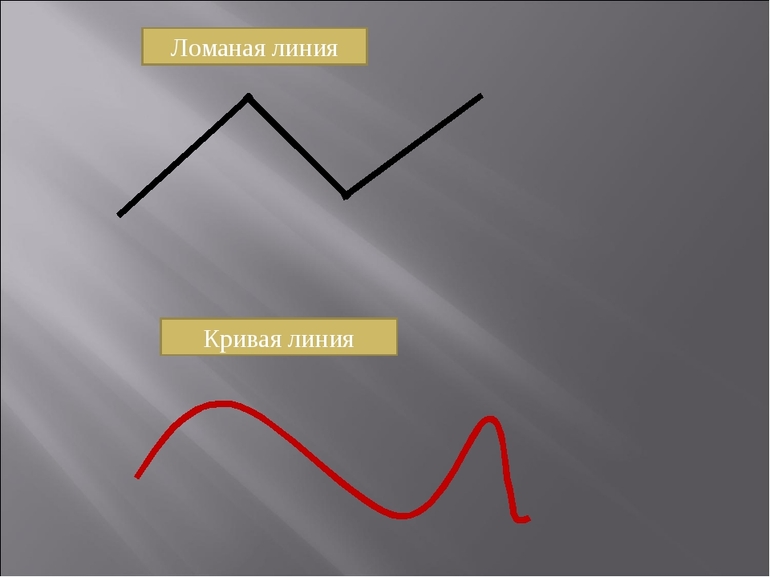
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.
В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.
Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.
Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.
Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.
Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.
Математическое определение
Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула <1, 2, n — 2>, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.
Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).
Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.
Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:
Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.
Основные разновидности ломаных
Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.
Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.
Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:
Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).
Базовые понятия
Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.
Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.
Особенности построения многоугольников
В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.
Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.
Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.
Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:
Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.
Ключевые нюансы
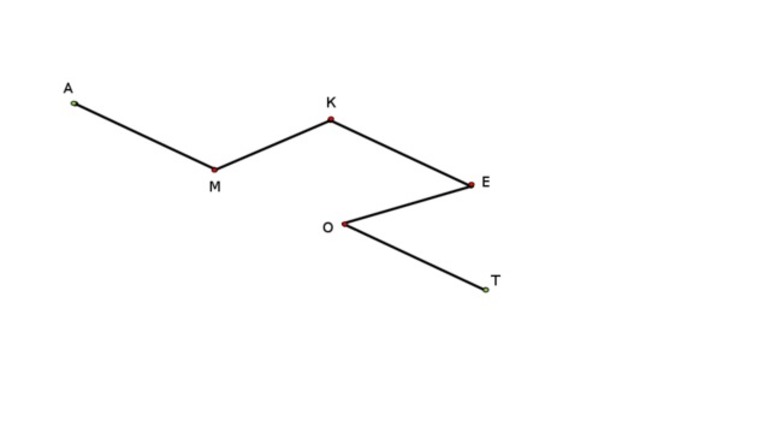
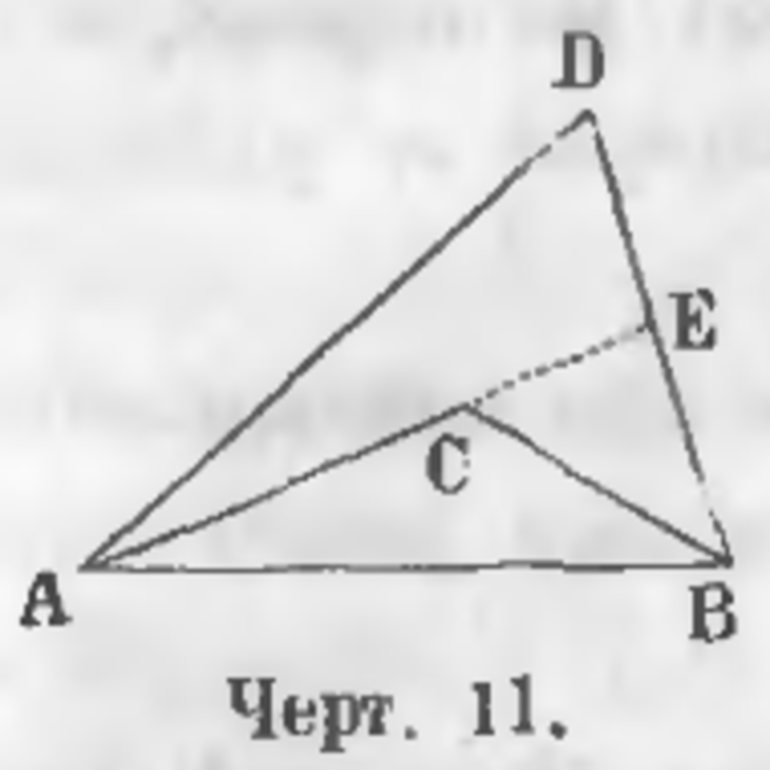
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.
Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:
Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.
Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.
Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.