что такое закон архимеда
Что такое закон архимеда
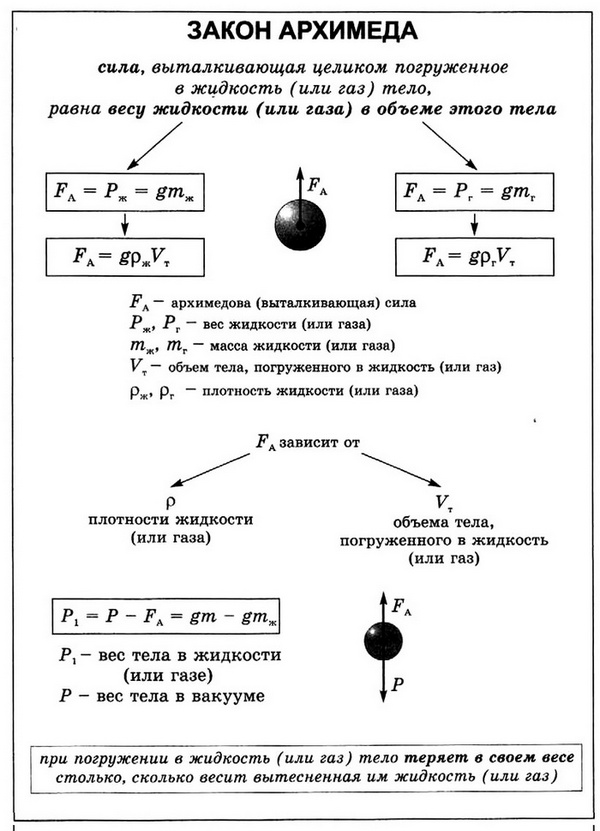
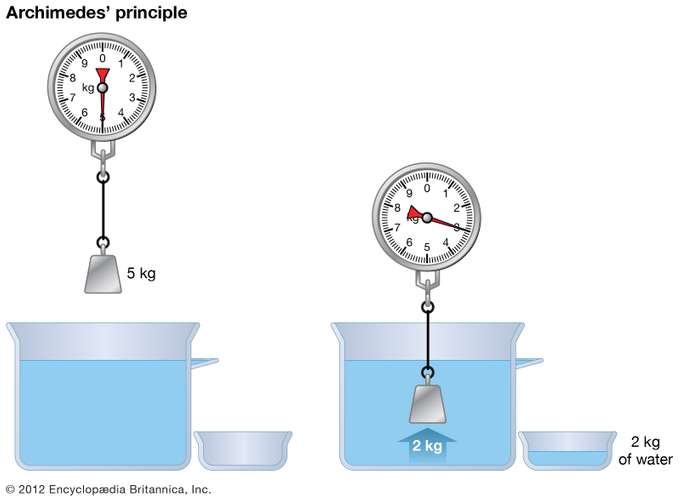
Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.
FА = pж • g • V ж = m ж • g = P ж
где: FА — Архимедова сила, pж — плотность жидкости, g — ускорение свободного падения, Vж — объем жидкости, mж — масса жидкости, Pж — вес жидкости.
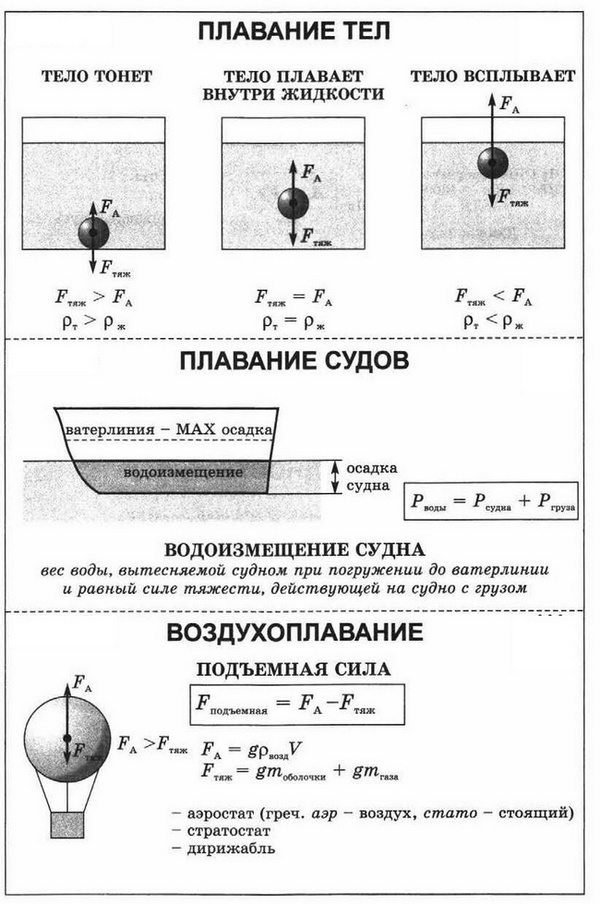
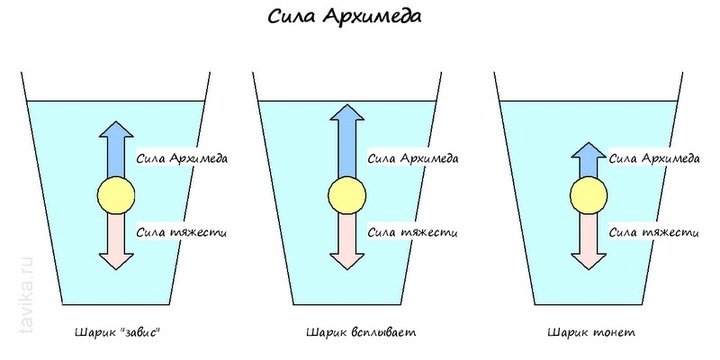
Плавание — это способность тела удерживаться на поверхности жидкости или на определённом уровне внутри жидкости. Н а любое тело, находящееся в жидкости, действуют две силы, направленные в противоположные стороны: сила тяжести и архимедова сила. Сила тяжести равна весу тела и направлена вниз, архимедова же сила зависит от плотности жидкости и направлена вверх.
Условие плавания тела на поверхности жидкости: для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой: Fв = М • g
Конспект урока «Архимедова сила».
1 Комментарий
Выталкивающей силы Архимеда в природе нет. Смотрите книгу «Новая Физика»
Добавить комментарий Отменить ответ
Конспекты по физике:
7 класс
8 класс
9 класс
10-11 классы
Найти конспект:
О проекте
Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!
Закон Архимеда для чайников
Обновлено: 09 Февраля 2021
Рассказываем историю открытия и объясняем, почему он важен.
Кто такой Архимед?
Древнегреческий ученый и изобретатель из Сиракуз. Жил в 3-м веке до нашей эры и сделал много открытий в геометрии, заложил основы механики и гидро- и аэростатики. К последним двум относится закон Архимеда.
Как был открыт закон Архимеда?
По распространенной версии, Архимед получил задание от царя Гиерона определить, из чистого ли золота сделана корона. Ученые того времени уже понимали связь между объемом и удельным весом вещества, но корона была неправильной формы. Архимед размышлял над тем, как измерить ее объем.
Решение пришло, когда он принимал ванну (точнее, тазик с водой). Ученый заметил, что когда тело погружается в воду, ее уровень становится выше. Это навело на мысль, что тело вытесняет объем воды, равный собственному объему.
Впоследствии оказалось, что этот закон применим и для предметов, помещенных в газовую среду.
Почему так происходит?
На погружаемое тело действует выталкивающая или подъемная сила (сила Архимеда), равная весу объема вытесненного вещества — жидкости или газа. Это и есть закон Архимеда.
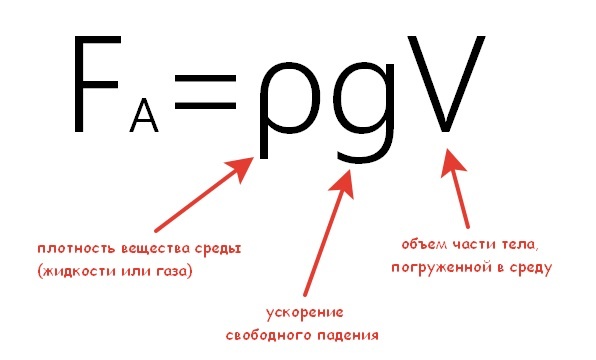
Сама формула силы Архимеда выглядит так:
Чтобы понять, погрузится тело или нет, нужно высчитать его силу тяжести:
Но можно обойтись знанием плотности вещества, из которого состоит объект, и вещества среды, в которое он может погрузиться. Тогда получаем:
Как это работает в жизни?
С явлением, описанным законом Архимеда, мы сталкиваемся постоянно. Благодаря этому знанию можете рассчитать конструкцию огромного корабля, который не утонет, и воздушного шара, который поднимется вверх.
Хотя для таких расчетов, конечно, знания основного закона статики недостаточно. Помочь разобраться в теме и сделать точные вычисления могут специалисты ФениксХелп.
Аксиома трёх шаров, или Все законы Архимеда
В трудах нескольких известных представителей античной науки имеются ссылки на утерянный трактат Архимеда «О плавающих телах». Оказывается, в нём было не четыре, а семь «теорем» и говорилось не об одном, а о двух законах: одному закону подчинялись микроскопические погружённые частицы, а другому – макроскопические тела. Со вторым законом мы знакомы, но сам Архимед начинал свой трактат с первого.
Вот первая «теорема» Архимеда: все жидкости на Земле находятся под давлением веса собственных и вышерасположенных слоёв; любая жидкость состоит из слоёв одинаковых, неподвижных и равноудалённых частиц, находящихся в состоянии взаимного отталкивания и относительного равновесия.
Эта «теорема» сейчас доказывается простым опытом: в стеклянную банку бросаем зажжённую спичку и накрываем банку крышкой; когда движение потоков неравномерно задымлённого воздуха в банке прекращается, плавно поворачиваем банку вокруг вертикальной оси симметрии и видим, что воздух в банке поворачивается вместе с ней, оставаясь неподвижным относительно её стенок. Это наблюдение и говорит нам о статическом взаимодействии неподвижным молекул воздуха с неподвижными молекулами стекла. С водой этот опыт проделывается ещё проще, только количество и вес воды в банке должно быть небольшим. Ответ на вопрос «Почему мало воды?» даёт сам Архимед.
Вот вторая «теорема»: между неподвижными частицами «идеальной сдавленной жидкости» нет механического взаимодействия и нет силы трения; давление в жидкости образуется не только за счёт веса всех вышерасположенных слоёв частиц, но и «стремлением жидкостей к округлостям». И в этом нет противоречия, ведь о способности статических атомов и молекул к движению взаимного отталкивания и к взаимодействиям на расстояниях, во много раз превышающих линейные размеры самих атомов и молекул, нам давно известно, но первым об этом догадался, пожалуй, именно Архимед. А вот «стремление жидкостей к округлостям» Архимед объяснял стремлением их частиц друг к другу, очевидно, не догадываясь о том, что круглые капли дождя, к примеру, формируются симметричным атмосферным давлением на них, а не стремлением частиц воды друг к другу.
Сам Архимед объясняет эту закономерность опять же «стремлением жидкостей к округлостям»: дескать, сдавливание частиц происходит не по прямой линии, а так, что два крайних шара давят на средний чуть-чуть снизу вверх или чуть-чуть сверху вниз. Пусть такой «механистический» подход нам и кажется наивным, но испарение жидкостей путём «самовыдавливания» частиц и принудительную диффузию частиц жидкостей в межмолекулярное пространство других веществ Архимед объяснил просто блестяще.
Для ясности тут остаётся только добавить, что частицы жидкостей не являются строго неподвижными, а колеблются или вибрируют («дрожат»), что и облегчает их выдавливание или «вдавливание». Кроме того, способность атомов и молекул к движению взаимного отталкивания прямо пропорциональна их температуре, определяемой интенсивностью внутриатомных движений компонентов атомов и колебательных движений самих атомных ядер. Поэтому все вещества при нагревании расширяются.
Получается так, что первые три «теоремы» из трактата «О плавающих телах» были «безвозвратно утеряны» только сторонниками молекулярно-кинетической теории. Зато, четыре последующих дошли до нас, можно сказать, в первозданном виде:
«Тела, равнотяжёлые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая их часть не выступает над поверхностью жидкости и не будут двигаться вниз (Однако «равнотяжёлых с жидкостью» тел в природе не существует, если только это не сама эта жидкость и не рыбы с плавательным пузырём или подводные аппараты, созданные человеком; Архимед мог употребить эту «теорему» лишь для доказательства всех последующих – прим. авт.);
тело, более лёгкое, чем жидкость, будучи опущено в эту жидкость, погружается настолько, чтобы объём жидкости, соответствующий погружённой части тела, имел вес, равный весу всего тела;
тела, более лёгкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх силой, равной тому весу, на который жидкость, имеющая равный объём с телом, будет тяжелее этого тела;
тела, более тяжёлые, чем жидкость, опущенные в жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объёме, равном объёму погружённого тела».
Вот и всё. Таким образом, весь трактат «О плавающих телах» мог представлять собой лист исписанной бумаги. Но мы говорим ещё проще и короче: дескать, погружению тела всегда препятствует вес вытесненной жидкости (газа) или вес жидкости (газа) в объёме тела. И это «просто» работает… Однако наука – чтобы не стоять на месте – считает, что вес вытесненной жидкости тут уже ни при чём, и само появление выталкивающей силы происходит по причине положительной разницы разновекторных давлений среды, действующих на погружённое тело.
Согласно этих представлений, вытесняющую силу в законе Архимеда предлагается вычислять через дифференцирование давления по высоте столба той же воды и путём интегрирования давлений воды по всем точкам поверхности погружённого тела. Что ж, логично. Правда, на всей Земле-матушке вы не сыщете чудака, который бы эти вычисления когда-либо применил на практике и высчитал бы эту «сумму-разницу» давлений для конкретного погружённого тела. Но, видимо, на то она и наука, чтобы не иметь ничего общего с понятной для всех простотой и предлагать нам только то, что невозможно использовать и, порой, даже себе представить.
Сам Архимед с таким научным объяснением своего закона не смог бы согласиться в принципе. А почему? А потому, что у него уже был трактат «О равновесии плоских фигур» и была своя логика. Вот и мы сейчас тоже возьмём для погружений максимально плоский кружок неизвестного вещества и простую логику Архимеда.
Итак, при погружении любого тела возможны только два последствия: либо тело всплывает на поверхность, либо же оно опускается на самое дно – пусть даже Марианской впадины. Наука объясняет это так: если давление воды под плоским кругом всегда больше, чем давление воды над кругом, то на него и действует всегда архимедова сила, равная разнице этих давлений; если разница этих давлений большая и она больше веса самого тела, то погружённое тело всплывает; если разница между давлением снизу и давлением сверху относительно небольшая и она меньше веса погружённого тела, то оно тонет. Но Архимед бы тут сказал, что в действительности всё может происходить и с точностью до наоборот: если давление воды под кругом намного больше, чем давление воды над ним, то круг не всплывает, а быстро-быстро тонет…
Давление в воде или давление воды на воду равно весу выше расположенного столба воды и весу столба атмосферы (последнее учитывать не будем). Если давление на воду столба воды, включающем наш круг в виде основания, больше, чем давление на воду соседнего аналогичного по высоте и объёму столба воды, но без круга, то тело тонет; если давление на воду столба воды с кругом меньше, чем давление на воду соседнего столба воды без круга, то тело всплывает. Прав Архимед.
Большая разница давлений над и под кругом может быть обусловлена двумя причинами – большой плотностью вещества круга (тело тонет). и малой плотностью вещества круга (тело всплывает). Выходит, что математический подход к вычислению вытесняющей силы или к определению плотности погружённого тела через геометрию тела и разницу давлений на погружённое тело никакого смысла не имеет. Вывод: вытесняющая сила по-прежнему везде и всюду равна только весу вытесненной среды и не зависит от плотности погружённого тела.
Однако в природе действует ещё один закон, о существовании которого сам Архимед уже знал, когда формулировал свои первые «теоремы» в трактате «О плавающих телах». Этот закон всегда действует в средах из подвижных твёрдых частиц, между которыми существует механическое взаимодействие и силы трения. То есть это «антизакон Архимеда», который действует в сыпучих или в зыбких средах. Архимед и формулирует свои первые «теоремы» совершенно так, чтобы жидкость по своим свойствам максимально отличалась, скажем, от речного песка.
Опыт: на дно стеклянной банки помещаем свинцовую пулю или гайку и заполняем банку сухим речным или сахарным песком; ставим банку на вибростенд… и видим, что массивное тело «всплывает» на поверхность вибрирующего и подвижного песка.
Подобные опыты ставит и сама Природа. К примеру, в черте города Екатеринбурга есть Шарташские каменные палатки. Горожане считали их скалами-останцами и вершиной древней каменной горы. В тридцатых годах городские власти решили «разжиться» камнем для нужд города, но гранита под скалами и рядом с ними не нашли. Оказывается, эти скалы покоятся на многометровой толще осадочных пород из песка и глины. Люди не знали о существовании «антизакона Архимеда» и сделали вывод: мол, эти скалы притащил на себе гигантский ледник, сползавший с Северного («верхнего») полюса земного шара под действием своей тяжести… Скалы огромных размеров «всплыли» по всему земному шару по причине частых землетрясений, подчиняясь третьему закону Архимеда.
Третий закон Архимеда тоже можно свести к «аксиоме трёх шаров», только средний шар или мяч нужно взять гораздо большего размера и веса, чем два крайних. Тогда при попытке удержать массивный шар давлением на него двух крайних шаров эти два шара обязательно будут смещаться вниз. Впрочем, это тоже шутка, ибо в никаких теоретических доказательствах законы Архимеда не нуждаются – они самодостаточны сами по себе, их нужно просто однажды прочитать.
Однако существует и четвёртый закон Архимеда. Этот закон гласит: на тела, герметично прикреплённые ко дну или стенкам сосуда, действие архимедовых сил становится асимметричным и они из выталкивающих превращаются в силы прижатия тел к этим поверхностям. К примеру, ложки, вилки, утюги и другие тела с гладкой поверхностью «прилипают» к гладкой и потной коже человека по причине атмосферного прижатия этих тел, а не по причине «биомагнетизма» или «посылов» Кашпировского. Подчиняясь четвёртому закону Архимеда, «работают» все, так называемые, присоски и кессоны. Но об этом в теме «Закон Архимеда», как правило, даже не упоминается.
Таким образом, в природе существуют и действуют сразу четыре закона Архимеда, из которых люди по-настоящему не знают и не понимают ни одного. И виновата в том только наука.
P. S. Архимеда сейчас считают чуть ли не основоположником математической физики. Это ещё одно заблуждение. Да, действительно, для объяснения рычага, равновесия плоских фигур и вычисления размеров Солнца им привлекались элементарные познания в геометрии, основанные на теореме Пифагора. Кроме того, он разделил длину окружности на её диаметр, измеренные с помощью нитки и линейки, и вычислил число Пи с точностью до четвёртого знака; ещё Архимед зачем-то вычислял отношения площадей шара, вписанного в цилиндр, и этого цилиндра…
Зато, с другой стороны, Архимед не стал высчитывать объём золотой короны, как это попытался бы сделать каждый «придворный» математик, а просто сунул её в воду и придал всей вытесненной при этом воде форму прямоугольного параллелепипеда. Архимедовым способом определения объёма сложных фигур, в котором нет даже намёка на математическую науку, сейчас при необходимости может воспользоваться каждый.
Главная заслуга Архимеда перед реальной физической наукой в том, что он математическим и теоретическим способам познания впервые противопоставил экспериментальные и сделал вес силой, заложив тем самым фундамент и гравитационной физики. И в этом он опередил Ньютона примерно на 1800 лет.
Парадокс закона Архимеда
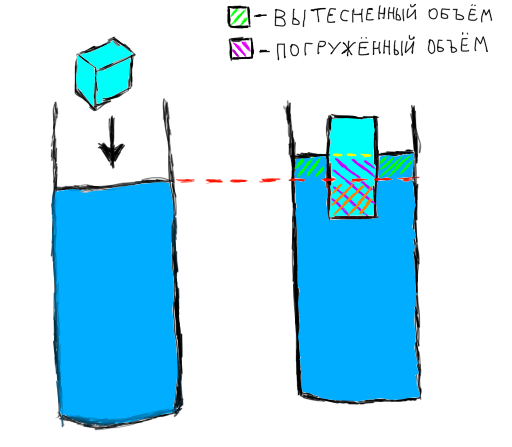
Существуют две разные формулировки закона Архимеда: «выталкивающая сила равна весу жидкости в объёме погружённой части тела» и «выталкивающая сила равна весу вытесненной телом жидкости». На первый взгляд кажется, что эти формулировки эквивалентны, ведь объём вытесненной жидкости равен погружённому объёму. Но на самом деле это абсолютно неверно. Чтобы понять почему, взглянем на рисунок.
В стакан с водой мы опускаем кубик льда. Красной пунктирной линией обозначен старый уровень воды, жёлтой — новый. Зелёным заштрихован вытесненный объём, фиолетовым — погружённый, а оранжевым — тот объём льда, который погружён ниже красной линии. Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому. Но как видно из рисунка, оранжевый объём является частью фиолетового. Фиолетовый объём намного больше оранжевого. А поскольку оранжевый равен зелёному, фиолетовый больше зелёного. Это означает, что погружённый объём больше вытесненного.
Нетрудно понять, что объём погружённой части всегда будет больше или равен вытесненному. Ведь вытесненный объём равен тому объёму тела, который погружён ниже старого уровня жидкости, а он, в свою очередь, является частью общего погружённого объёма. Значит, вытесненный объём будет равен погружённому только в том случае, когда вся погружённая часть тела находится ниже старого уровня жидкости.
Но если погружённый и вытесненный объёмы не равны, возникает вопрос: какая же формулировка закона Архимеда верна? Чтобы ответить на него, вспомним, как выводится закон Архимеда.
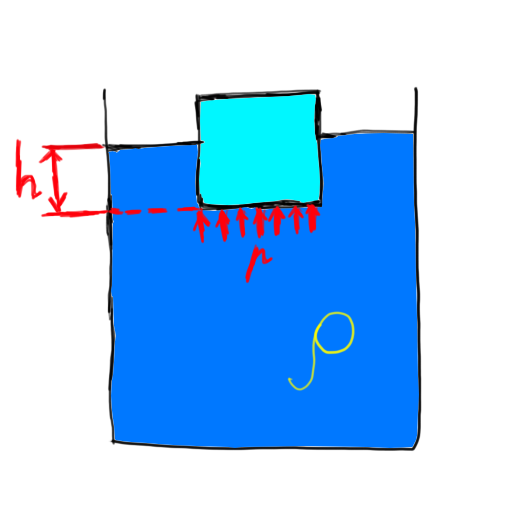
Вернёмся ко льду в воде. Пусть он погружён на глубину h. В любой точке на этой глубине давление равно ρgh, где ρ — плотность жидкости, g — ускорение свободного падения, h — глубина. По закону Паскаля давление передаётся без изменений во всех направлениях. Таким образом, это давление жидкость оказывает на нижнюю грань кубика. Пусть её площадь равна S. Тогда сила давления на нижнюю грань кубика равна ρghS = ρgV, где V — объём погружённой части кубика (V = hS). Эта сила и есть выталкивающая. Таким образом, получается, что выталкивающая сила равна весу жидкости в объёме погружённой части тела, а вовсе не весу вытесненной жидкости.
Из всего вышесказанного также следует, что водоизмещение корабля совсем не обязательно будет равно его массе (если под водоизмещением мы подразумеваем массу вытесненной воды). Поскольку корабль не тонет, сила тяжести, действующая на него, равна силе архимеда:
mg = ρgV (m — масса корабля, g — ускорение свободного падения, ρ — плотность воды, V — погружённый объём).
Разделив это уравнение на g, получим
Обозначим объём вытесненной воды как Vвыт. Поскольку
ρVвыт ≤ ρV ⇔ ρVвыт ≤ m.
Но ρVвыт — это масса вытесненной воды, то есть, водоизмещение. Следовательно, водоизмещение меньше или равно массе корабля.
Ситуацию, когда водоизмещение меньше массы корабля, проще всего наблюдать, когда корабль плавает в тесном доке. Даже если масса воды в доке меньше массы корабля, он всё равно не будет касаться дна, несмотря на то, что не будет вытеснять воду с массой, равной своей.
заполни изначально стакан до краев, чтобы жидкость выливалась, и не еби мозг
Но если погружённый и вытесненный объёмы не равны,
Кто тебе сказал, что они не равны?
«Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому. Но как видно из рисунка, оранжевый объём является частью фиолетового. Фиолетовый объём намного больше оранжевого. А поскольку оранжевый равен зелёному, фиолетовый больше зелёного. Это означает, что погружённый объём больше вытесненного.»
Зачем ты написал эту хуйню?
Или ты правда в нее веришь?
Даже если масса воды в доке меньше массы корабля, он всё равно не будет касаться дна
«На первый взгляд кажется, что эти формулировки эквивалентны, ведь объём вытесненной жидкости равен погружённому объёму. Но на самом деле это абсолютно неверно. Чтобы понять почему, взглянем на рисунок.»
Если я нарисую автора с тремя руками, это будет доказательством наличия у него трех рук?
Неправильно уже первое утверждение «Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому». Дальше эту куету не читал.
Тело, впихнутое в воду, выпирает на свободу с силой выпертой воды телом, впихнутым туды.)
Иначе получится неприятный казус. Вода должна подняться, но при поднятии ещё больший объём погружается воду, значит вода должна ещё чуть подняться; и так до того момента, пока весь предмет не будет погружён в воду! Приходим к выводу, что ни один предмет не может всплыть из воды, что неверно!
Вот ещё более интересная задачка про погружаемое тело и высоту столба жидкости вокруг него, Вам однозначно погравится https://zen.yandex.ru/media/id/5e4f1d8670d2aa13e1bf7948/oche.
Проблема Больцмановского мозга и как она появилась
Текстовая версия видео:
Допустим, что время движется именно в сторону максимальной энтропии. Что это значит для нашей Вселенной? Опять же, многое указывает на то, что в будущем наступит состояние с максимальной энтропией, термодинамическое равновесие, когда все частицы барионной материи будут двигаться почти с одинаковой скоростью. А Вселенная мало того, что и так огромная, так еще и расширяется, в общем скорость этих самых частиц будет практически нулевая, будет колебаться возле абсолютного нуля. Такое состояние еще называют «Тепловой смертью Вселенной». Существуют аргументы против того, что это произойдет, но опять же, не буду начинать все перечислять.
Итак, в чем же проблема с энтропией и вечной Вселенной. Если бы Вселенная была вечной, то мы бы не наблюдали таких объектов как, например, звезды, туманности и тем более жизнь, ведь все температуры уравнялись бы, было бы состояние термодинамического равновесия, то есть максимальной энтропии.
Так вот, в конце 19 века стоял вопрос. Если Вселенная вечна, то почему она не находится в состоянии с максимальной энтропией, почему не все имеет одинаковую температуру, ведь неизбежно температуры должны были уравняться за бесконечный промежуток времени, что следовало из законов термодинамики.
Получается такой вот парадокс. Подумайте, как бы вы его разрешили.
Некий физик, Людвиг Больцман, предложил аж два решения и надо отдать ему должное – додуматься до такого в те времена (19 век) было необычайно умно.
Что же он предложил? Одно из решений заключалось в том, что Вселенная начала свое существование с состояния с низкой энтропией. Другими словами, она была очень горячей в недалеком прошлом и понемногу постепенно охлаждается.
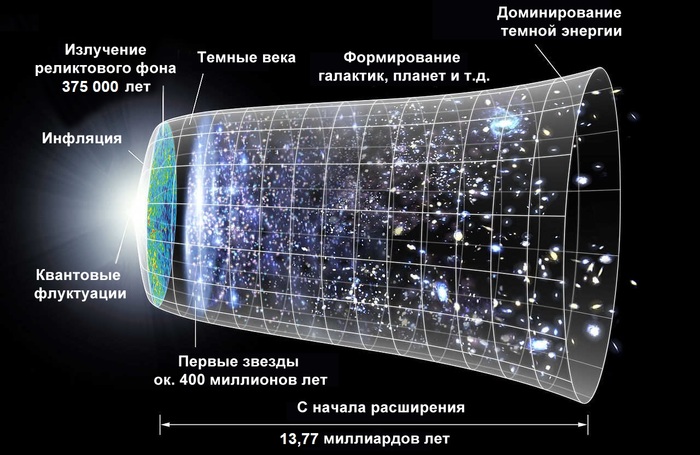
Сейчас мы знаем, что именно так и было – Вселенная начала свое существования с очень низкой энтропией относительно недавно по сравнению с вечностью – примерно 13.8 миллиардов лет назад (это один из нетривиальных способов доказать Большой Взрыв). У нас даже есть фотографии той горячей эпохи.
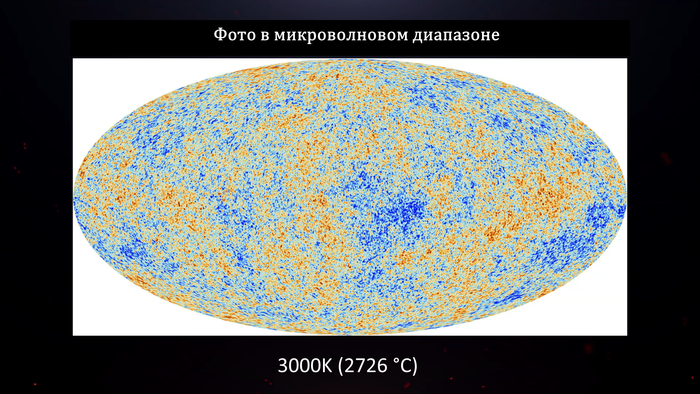
Вот, например, фотография Вселенной примерно 400 тысяч лет после Большого Взрыва, когда она имела температуру около 3000 кельвинов (2726 °C). Казалось бы, что тогда наоборот термодинамическое равновесие было больше и соответственно энтропия больше, чем сейчас, но это не так. Второе объяснение Больцмана более необычное. Он предположил, что да, Вселенная существовала вечно и в ней вечно было термодинамическое равновесие, максимальная энтропия, в общем практически везде одинаковая, холодная Вселенная. Но Больцман пошел дальше и высказал гипотезу, что атомы, наполняющие эту Вселенную, в ходе хаотических флуктуаций случайно собрались таким невероятным образом, что в итоге в одной части Вселенной случайно появилось все то, что мы наблюдаем: планеты, звезды, туманности и так далее.
Казалось бы, что это полнейший бред, такого произойти не может. Но на самом деле нет. В вечной Вселенной такое событие произойдет бесконечное количество раз – из хаоса появятся структуры любой сложности, но чем более сложная структура, тем меньшая вероятность ее случайного появления. Просто бесконечность, да и вообще очень большие или очень маленькие числа для нас неинтуитивны.
Существует очень известная «теорема о бесконечных обезьянах», которая утверждает, что абстрактная обезьяна, ударяя случайным образом по клавишам пишущей машинки в течение неограниченно долгого времени, рано или поздно напечатает любой наперёд заданный текст.
В общем, если событие имеет сколь угодно малую вероятность, то за бесконечное количество времени это событие произойдет с вероятностью 100%. Приведу еще примеры. Если на бильярдном столе шары будут двигаться вечно, то за бесконечное количество времени они случайно хотя бы на момент создадут любой возможный узор из шаров, хотя понятно, что такие события маловероятны, большинство времени они будут просто хаотически двигаться.
Представим, что мы заключили газ в какой-то коробке, можете представить, что ваша комната и воздух в ней являются такой коробкой с газом и что эта система (система из газа в коробке), является изолированной – то есть не может обмениваться энергией с внешним миром.
Газ в коробке будет стремиться к максимальной энтропии, к термодинамическому равновесию, что выглядит как хаотическое равномерное движение всех частиц, но существует шанс, мизерный, что газ случайно соберется на одной стороне коробки. Энтропия такой системы уменьшится, но ненадолго, газ опять быстро достигнет термодинамического равновесия.
За бесконечное количество времени произойдет бесконечное количество таких событий – газ соберется в одной стороне коробки бесконечное количество раз. Вообще, любая конфигурация, не нарушающая закон сохранения импульса и энергии произойдет в этой коробке, газ соберется в одну точку, сформирует различные фигуры, даже случайно напишет слово «энтропия» и случайно создаст микромодель, например, Солнечной Системы.
Парадокс действительно можно было решить этим объяснением, но позже физики пришли к следующим выводам: вероятность появления видимой Вселенной в результате случайных тепловых флуктуаций чрезвычайно мала, речь идет о вероятностях порядка 1 до Числа Грэма. Чем менее сложная структура и с чем меньшего количества частиц она состоит, тем большая вероятность появления такой структуры в вечной Вселенной. Звезда в результате хаотического движения частиц появится с большей вероятностью, чем галактика. Планета появится с большей вероятностью, чем звезда.
Человек появится с большей вероятностью, чем планета. Мозг, осознающий себя появится с большей вероятностью, чем человек. Согласно такой логике, с большей вероятностью ты, осознающий себя, на самом деле являешься просто случайно собравшимся мозгом из частиц во Вселенной с термодинамическим равновесием, причем все твои воспоминания — это иллюзия, они тоже появились случайно. Все, что ты видишь, знаешь и наблюдаешь – тоже иллюзия, на самом деле ты лишь мозг случайно появившийся посреди хаоса.
Сейчас в научных кругах проблему Больцмановских мозгов часто называют, в переводе на русский, «ложный наблюдатель» (freak observer), обычно это касается работ посвященных Мультивселенной. Если существует бесконечное число Вселенных, ну или очень большое число Вселенных с различными физическими законами, то математически большая вероятность, что во всем мультуме Вселенных больше мозгов Больцмана, а не обычных живых существ, и осознающий себя ты, опять же, с большей вероятностью это Больцмановский мозг, а не тот, кем себя представляешь.
Так в конце концов, все-таки я – Больцмановский мозг и все мои воспоминания поддельны, или нет?
Это нельзя проверить, это не наука, в это можно верить, либо не верить, а это уже решать вам. Добавлю еще, что некоторые ученые называют проблему Больцмановского мозга глупостями, а некоторые постоянно придумывают способы как-то ее опровергнуть и привести аргументы против, да и вообще проблема Больцмановского мозга возникает только при некоторых допущениях. Не вижу смысла более глубоко раскрывать эту тему, все основное я рассказала. Моей целью было предоставить пищу для размышлений. Приятного аппетита =)
Гидростатистический парадокс)
Это глобальное потепление во всем виновато
Что такое «парадокс убитого дедушки» и как его решить
Путешествия во времени — одна из самых интригующих фантастических концепций. Но она вызывает много вопросов — как у физиков, так и у философов, — а также может привести к разным парадоксам. «Парадокс убитого дедушки» — один из них.
Концепция путешествий во времени вовсю используется в литературе и кино, вне зависимости от жанров. Зачастую в центре всех таких историй — изменения, внесенные путешественником в события прошлого, которые приводят к настоящим катастрофам в будущем. Стоит вспомнить хотя бы рассказ Рэя Брэдбери «И грянул гром».
Эта дилемма, также известная как «парадокс убитого дедушки», представляет собой главное возражение физиков и философов против путешествий во времени: возможное нарушение причинности. И хотя путешествия во времени пока лишь спекуляция, вероятные результаты нарушения принципа причинности и того, как природа может их предотвратить, — предметы горячих споров среди таких ученых, как Стивен Хокинг и Кип Торн.
Что такое «парадокс убитого дедушки»
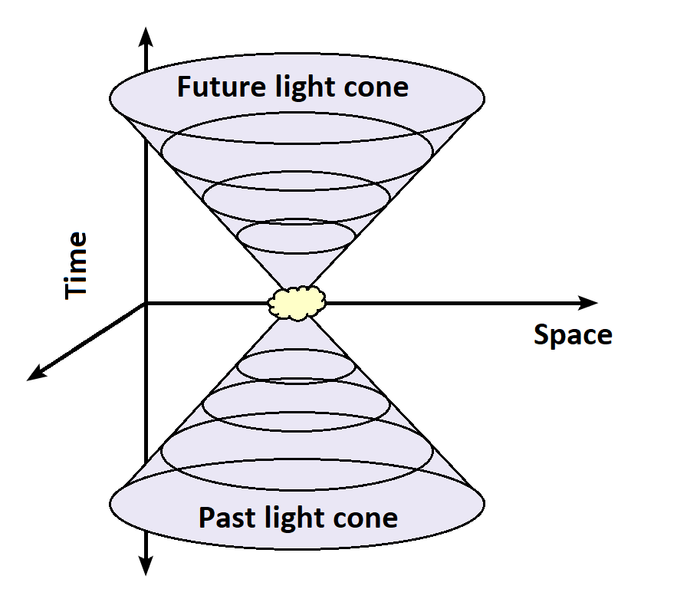
Согласно Специальной теории относительности, прошлое (причина) всегда предшествует будущему (следствию) / © Helen Klus
Давайте представим себе сценарий, в котором молодой талантливый изобретатель — назовем его Евгением — создает в 2018 году машину времени. Так как Евгений никогда не знал своего дедушку, он решает отправиться в прошлое, чтобы встретиться с ним. После тщательного исследования он выясняет, где именно находился его дедушка — все еще молодой и холостой — в 15:43, 22 ноября 1960 года. Он садится в машину времени и начинает свой путь.
К сожалению, Женя все воспринимает буквально, и, когда он выяснил, где будет его дедушка, он отправился именно в то самое место. Он «приземляется» прямо туда, где в этот момент должен находиться его дедушка… с весьма предсказуемым результатом. Проведя быстрый ДНК-тест, он понимает, что это действительно был отец его отца, садится обратно в машину и ждет своего исчезновения.
Игорь Дмитриевич Новиков / © Фотоархив ГАИШ МГУ
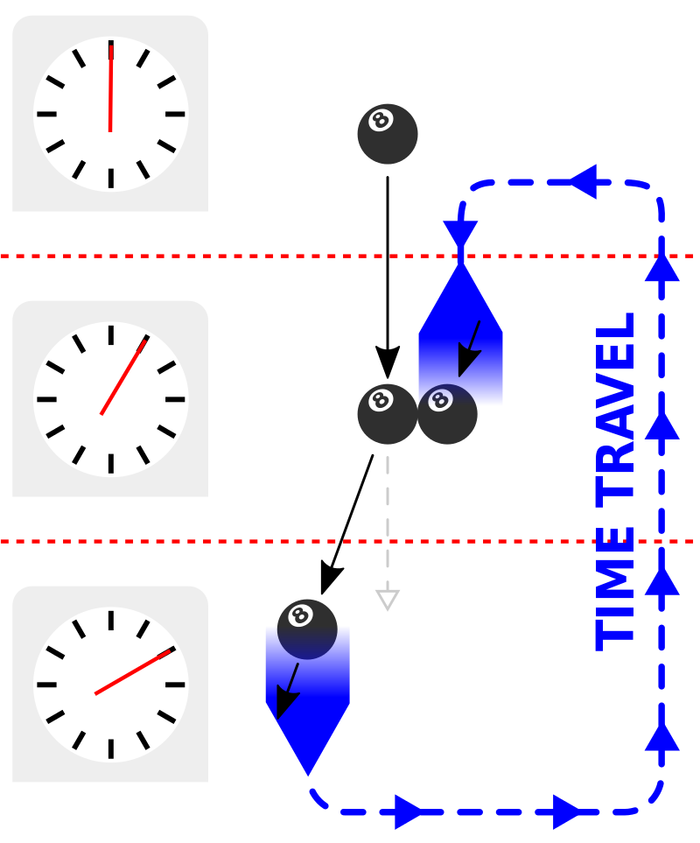
Эта идея позднее была расширена студентами Калтеха Фернандо Эшеверриа и Гуннаром Клинхаммером совместно с Кипом Торном. В своей статье они представили бильярдный шар, брошенный в прошлое через червоточину по траектории, которая в итоге помешала бы ему попасть в нее. Они утверждали, что физические свойства червоточины изменили бы траекторию шара таким образом, что он бы не смог помешать сам себе, или что шар не может попасть в червоточину по причине фактического вмешательства со стороны.
Таким образом, если следовать теории Новикова, любые действия, предпринятые путешественником во времени, становятся уже свершившейся историей, а наблюдателям эти события не дает увидеть горизонт Коши.
По возвращении в 2018 год наш Евгений обнаруживает, что дом его семьи пропал, как и другие следы его существования. Прочитав о теории Новикова и бильярдных шарах ученых из Калтеха, он проклинает Вселенную за бездействие. И в этот момент понимает, что, может, Вселенная не вмешалась, так как для этого требовалось некоторое корректирующее действие. Он бежит обратно к машине времени, чтобы изменить собственные действия и спасти свое будущее.
Решение Эшеверриа и Клинкхаммера / © Wikipedia
Решение Новикова может выглядеть несколько надуманным, так как для него определенно требуется множество механизмов, пока неизвестных физике. Именно по этой причине это решение «парадокса убитого дедушки» научное сообщество отвергает.
Может ли быть более экономное решение парадокса, построенное на уже существующих аспектах физики, введенных другими теориями? Оказывается, такая гипотеза, как многомировая интерпретация квантовой механики, может его предоставить. Многомировая интерпретация квантовой механики спешит на помощь!
Многомировую интерпретацию квантовой механики предложил Хью Эверетт III в 1950-х в качестве решения проблемы коллапса волновой функции, наблюдаемой в известном эксперименте Юнга с двумя щелями.
По мере прохождения через щель электрон может быть описан волновой функцией с конечной вероятностью прохождения либо через щель № 1, либо через щель № 2. Когда электрон появляется на экране, он выглядит размазанным, словно волна. А в других случаях проявляет себя как частица. Это называется коллапсом волновой функции. Другими словами, волна будто исчезает, а на ее месте остается частица. Это, в свою очередь, ключевой фактор Копенгагенской интерпретации квантовой механики. Но ученые не понимали, почему коллапсирует волновая функция.
Эверетт задал другой вопрос: а коллапсирует ли волновая функция вообще?
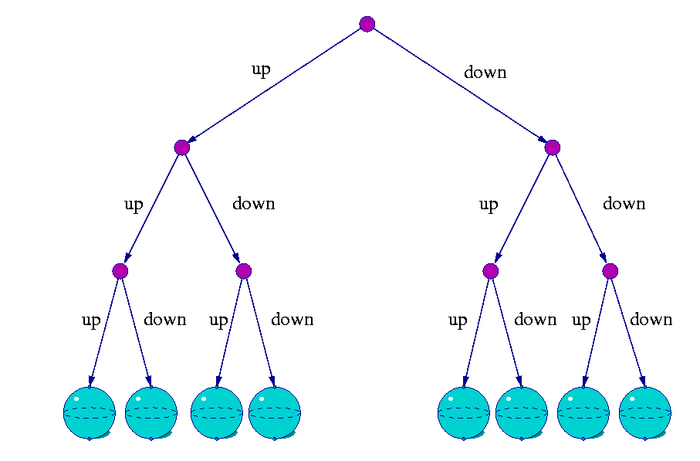
Он представил ситуацию, при которой волновая функция продолжает расти по экспоненте, не коллапсируя. В итоге вся Вселенная обретает одно из двух возможных состояний: «мир», в котором частица прошла через щель № 1, и «мир», в котором частица прошла через щель № 2. Эверетт утверждал, что такое же «деление» состояний происходит во всех квантовых событиях, многочисленные исходы которых существуют в разных мирах в состоянии суперпозиции. Волновая функция для нас выглядит так, будто она коллапсирует, поскольку мы живем в одном из таких миров, не способных взаимодействовать друг с другом.
Диаграмма разделения миров согласно многомировой интерпретации квантовой механики / © Wikipedia
Следовательно, когда Евгений прибывает в 1960 год, Вселенная разделяется. Он уже находится не в том мире, из которого прибыл (пусть это будет Мир № 1). Вместо этого он создал и занял новый мир. Когда он путешествует в будущее, то движется вместе с хронологией этого мира. Он никогда не существовал в нем и, по сути, никогда не убивал своего дедушку. Его дедушка продолжает существовать в добром здравии в Мире № 1.
Конечно, ни одно из предложенных решений и гипотез не делает путешествия во времени реальностью. Специальная теория относительности Эйнштейна и ограничения на скорость объекта с массой ставят серьезные преграды для этого. Тем не менее они предоставляют интересные решения головоломке. По иронии судьбы самое правдоподобное решение «парадокса убитого дедушки» исходит из единственной физической гипотезы, породившей еще больше фантастических историй, чем многие другие идеи и гипотезы, высказанные учеными за последнее столетие.
Любопытно, что многомировая интерпретация также может ответить на еще одну головоломку, связанную с путешествиями во времени. Если такая технология когда-то и станет чем-то большим, чем фантастика, где все путешественники во времени? Почему они до сих пор не прибыли к нам, чтобы рассказать о своем открытии?
Вероятный ответ — мы живем в первичном мире, в котором машинам времени суждено быть созданными. А изобретатели и их попутчики просто попадают в другие миры, которые сами и порождают. Если это действительно так, то изобретение машины времени приведет наш мир к тому, что из него пропадет множество физиков и изобретателей.
Аниме Закон Архимеда
Демон Максвелла | [Невозможные изобретения]
В древние времена самым простым, а иногда и единственным способом для достижения чего-либо невозможного человек считал обращение к помощи потусторонних сил.
Позже, вместе с бурным развитием наук появилась надежда, что технологический прогресс поможет устранить необходимость привлечения сверхъестественного для решения насущных проблем.
Но ведь потребности человека фактически не удовлетворимы, а границы желаемого расширяются намного быстрее, пределов достижимого.
Поэтому даже ученые иногда прибегают к помощи демонов, особенно когда им необходимо бросить вызов какому-нибудь фундаментальному научному закону. Например, второму началу термодинамики, неумолимая суровость которого, теоретически когда-нибудь приведет к концу своего существования всю нашу Вселенную.
Кстати, Томсон в 1851 году и сформулировал одно из определений второго закона термодинамики, который в его интерпретации звучит следующим образом: невозможен процесс, единственным результатом которого является получение системой теплоты от одного источника (теплового резервуара) и выполнение ею эквивалентного количества работы.
При этом Томсон опирался на исследования Сади Карно, который в 1824 году в своей работе «Размышления о движущей силе огня и о машинах, способных развивать эту силу», посвящённой паровым машинам, первым сформулировал идею, заложившую основу для понимания второго начала термодинамики:
при отсутствии разности температур теплота не может быть преобразована в работу; для постоянного производства работы тепловой машине необходимо иметь по крайней мере два тепловых резервуара с различными температурами — нагреватель и холодильник.
Но и здесь, если говорить о названиях, не все просто и однозначно. На самом деле, исторически первая формулировка закона и его определение «вторым началом термодинамики» принадлежат Рудольфу Клаузиусу.
Более того, понятие энтропии, её обозначение и название тоже были введены Клаузиусом в 1865 году.
Хотя, когда речь заходит об энтропии, большинство в первую очередь вспоминает Людвига Больцмана.
И раз речь, наконец, дошла до энтропии, то самое время вернуться к нашему демону.
Итак, «демон» впервые появился в письме, которое Максвелл написал Питеру Гатри Тейту 11 декабря 1867 года в виде описания мысленного эксперимента, гипотетически позволяющего нарушать второй закон термодинамики. Позже он снова появился в письме Джону Уильяму Стратту в 1871 году, и только потом он был окончательно представлен публике в книге Максвелла 1872 года по термодинамике под названием «Теория тепла».
В своих письмах и книгах Максвелл описывал агента, открывающего дверь между комнатами, как «определенное существо» («finite being»). Как уже упоминалось, Уильям Томсон, он же лорд Кельвин, первым использовавший слово «демон» для концепции Максвелла в журнале Nature в 1874 году, на самом деле имел в виду посредническую, а не злобную коннотацию этого слова.
Согласно описанию Максвелла суть его мысленного эксперимента состоит в следующем:
Но это было бы слишком здорово, практически прямой путь к созданию вечного двигателя.
Все надежды на привлечение «демона Максвелла» к такому нужному делу были развеяны в 1929 году Лео Сцилардом. Сцилард обратил внимание на то, что реальный демон Максвелла должен иметь какие-то средства измерения молекулярной скорости и что получение информации тоже потребует затрат энергии. Поскольку демон и газ взаимодействуют, следует учитывать общую энтропию газа и демона вместе взятых. Расход энергии демоном вызовет увеличение энтропии демона, которое будет больше, чем понижение энтропии газа.
Звучит исчерпывающе! Казалось бы, вопрос закрыт? Снова «невозможное изобретение»!
Поскольку нарушение законов физики, в отличие от прочих законов, не грозит перспективой наказания, а вот на премию типа Нобелевской нарушитель вполне может рассчитывать, то желающих представить миру свою версию демона Максвелла превеликое множество.
Только за последнее десятилетие было предпринято несколько эффектных попыток.
В 2010 году мысленный эксперимент в реальности удалось воплотить физикам из университетов Тюо и Токийского университета.
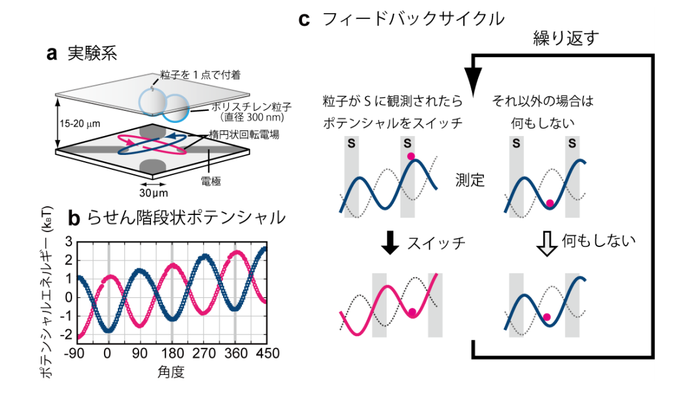
Японцы создали два связанных шарика полистирола диаметром 0,3 микрометра каждый. Один был прикреплен на поверхности стекла, а второй шарик-ротор мог вращаться вокруг первого.
Установку при этом заполняла жидкость. Её молекулы хаотично подталкивали шарики, создавая эффект броуновского движения. Поэтому, ротор мог вращаться с равной вероятностью, как по направлению часовой стрелки, так и против.
Авторы добавили слабое электрическое поле, которое создавало крутящий момент. Это был аналог лестницы, по которой шарик мог «взбираться», увеличивая потенциальную энергию. Иногда молекулы толкали ротор против действия поля (на подъём), а иногда в сторону поля (прыжок по ступенькам вниз). Но в целом ротор вращался туда, куда его толкало внешнее поле.
Но вот физики добавили «демона» — высокоскоростную камеру, наблюдающую за шариком, и компьютер, управляющий полем. Каждый раз, когда ротор в броуновском движении делал шаг против поля, компьютер сдвигал последнее так, что шарик мог повернуться, но когда ротор пытался вращаться обратно, поле блокировало его.
Так был создан аналог открываемой и закрываемой демоном Максвелла дверцы: ротор увеличивал свою энергию за счёт теплового движения молекул.
Законов природы, впрочем, установка не нарушает, поскольку для работы «демона» (то есть камеры, системы коррекции напряжения) необходима энергия. Но японцы подчёркивают, что данный опыт впервые на практике доказал реальность так называемого теплового насоса – варианта «демона Максвелла», теоретически обоснованного Лео Сцилардом в 1929 году. Такая машина извлекает энергию из изотермической окружающей среды и преобразует её в работу.
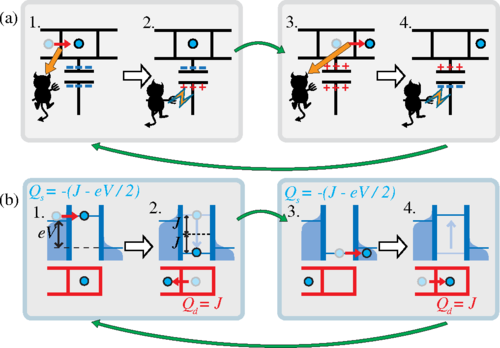
В 2016 году Физики из Финляндии, России и США создали электронную версию замкнутого (автономного) демона Максвелла. «Система» представляет собой одноэлектронный ящик, подключенный к внешнему потенциалу. Демон следит за зарядом на коробке. (Слева) Если электрон (синий) входит в ящик, демон немедленно захватывает его, прикладывая положительный заряд. (Справа) Если электрон покидает ящик, демон отталкивает его, прикладывая отрицательный заряд. Это электронный эквивалент того, как демон открывает или закрывает дверь для быстрых и медленных частиц в оригинальном мысленном эксперименте Максвелла.
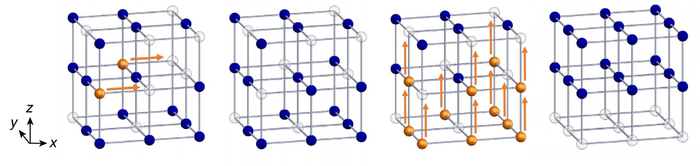
В 2018 году физики в США упорядочили систему из 50 помещенных в трехмерную оптическую ловушку атомов цезия с помощью реального аналога демона Максвелла, уменьшив при этом энтропию системы почти в 2,5 раза.
В оптической ловушке атомы захватываются с помощью двух поляризованных лазеров, которые создают периодический удерживающий потенциал.
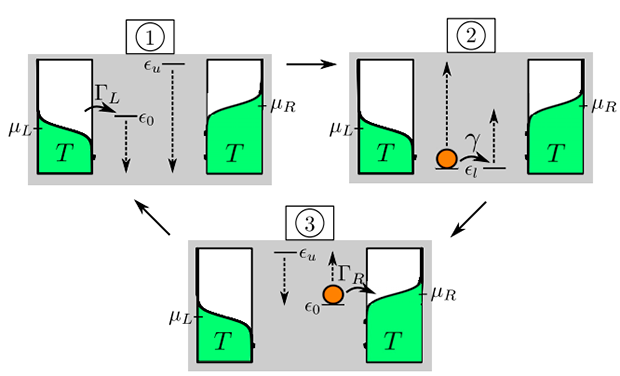
6 апреля 2020 года в журнале Physical Review B была опубликовано исследование, описывающее созданную учеными систему из двух квантовых точек с одноэлектронными переходами для оценки термодинамических характеристик демона Максвелла с учетом информации и возвратного действия измерений.
Они продемонстрировали возможность преобразования тепла в работу за счет информации и получили кривые зависимостей тепла и мощности от запирающего напряжения и степени туннелирования.
Это только самые удачные и поэтому самые нашумевшие эксперименты последних лет по созданию демона Максвелла.
Не стоит сомневаться, что попытки обмануть природу при содействии ловкого демона будут продолжаться и дальше до тех пор, пока они либо увенчаются успехом, либо вся Вселенная достигнет термодинамического равновесия…