что такое высота треугольника в геометрии 7 класс определение

Определение и свойства высоты треугольника

В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.

Определение высоты треугольника

Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.

Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).

Обычно высота обозначается буквой h (иногда как h_a – это означает, что она проведена к стороне a).

Высота в разных видах треугольников

В зависимости от вида фигуры высота может:

Свойства высоты треугольника

Свойство 1

Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).

Свойство 2

При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:

Свойство 3

Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.

Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.

Свойство 4

Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.

Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.

Источник

Способы нахождения высоты треугольника: теорема и формула

Определение высоты треугольника

Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.

Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.

Треугольники могут быть:

Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.

Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.

В геометрии высота треугольника обозначается буквой h.

В зависимости от типа треугольника высота может:

Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.

Для того чтобы определить графическое начертание высоты треугольника, необходимо:

Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.

Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:

A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B

Выглядеть графически это будет так:

Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.

Через площадь и длину стороны, к которой опущена высота:

где S — уже известная площадь треугольника,

Через длины всех сторон:

h = 2 p p × a p × b p × c a

где a, b и c — стороны треугольника,

p — его полупериметр.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длину прилежащей стороны и синус угла:

s i n a — синус угла прилежащей стороны.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через стороны и радиус описанной окружности.

Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:

где b, c — стороны разностороннего треугольника, к которым не опущена высота,

R — радиус описанной окружности.

Данная формула подходит только для нахождения высоты разностороннего треугольника.

Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:

где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.

Данная формула подходит только для нахождения высоты прямоугольного треугольника.

Нахождение высоты равнобедренного треугольника через основание и боковые стороны

Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.

Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.

Формула для нахождения высоты в этом случае:

b — равные боковые стороны.

Свойства высоты в равностороннем треугольнике

Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.

Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.

Высоту в таком треугольнике можно найти с помощью следующей формулы:

где а — сторона равностороннего треугольника.

Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:

а — сторона правильного равностороннего треугольника.

Нахождение высоты прямоугольного треугольника через его катеты

Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.

Важно отметить, что две другие высоты будут совпадать с катетами треугольника.

Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).

Причем гипотенуза также легко находится через катеты по теореме Пифагора:

Расчет высоты идет следующим образом:

где a, b и c — вышеупомянутые стороны треугольника.

Источник

Треугольник. Высота треугольника.

Высота треугольника – перпендикуляр, прочерченный из выбранной вершины треугольника на противолежащею его сторону. Для обозначения высоты треугольника используют букву h, к ней добавляется название той стороны, к которой она прочерчена: h_a, h_b, h_c,

Сторону треугольника, к которой прочерчена высота, называют основанием треугольника.

Высота треугольника может быть прочерчена к любой из трех сторон треугольника. Случается высота треугольника пересекает не само основание треугольника, а его продолжение. Так, высоты AD и ЕМ пересекают продолжения оснований ВС и FK.

Характерные особенности высоты.

В прямоугольном треугольнике высота, прочерченная из вершины прямого угла, разделит его на два треугольника, подобные первоначальному.

В остроугольном треугольнике две его высоты отделяют от него подобные треугольники.

Если треугольник остроугольный, то все основания высот принадлежат его сторонам, а у тупоугольного треугольника две высоты принадлежат продолжению сторон.

Три высоты в остроугольном треугольнике перекрещиваются в одной точке и эту точку обозначают как ортоцентр треугольника.

Источник

Высота треугольника

Всего получено оценок: 75.

Всего получено оценок: 75.

Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.

Определение

Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.

Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.

Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.

Как найти высоту треугольника?

Существует три стандартных способа нахождения высоты треугольника:

Через теорему Пифагора

Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.

Дано: равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.

Рис. 2. Рисунок к задаче.

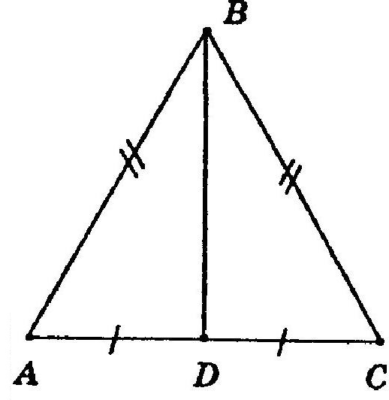
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.

Свойства высоты равнобедренного треугольника, проведенной к основанию:

Высоту обозначим, как ВD. DС найдем как половину от основания, так как высота точкой D делит основание пополам. DС=4

Высота – это перпендикуляр, значит ВDС – прямоугольный треугольник, а высота ВD является катетом этого треугольника.

Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.

Через площадь треугольника

Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.

Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.

Через тригонометрическую функцию

Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.

Рис. 3. Рисунок к задаче.

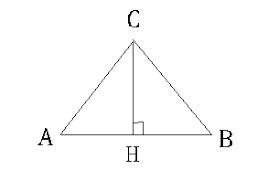
Угол известен, как и сторона. Выразим высоту треугольника:

Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.

Что мы узнали?

Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.

Источник

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные. На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник