что такое высота ромба в геометрии
Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Если у ромба – прямые углы, то он называется квадратом.
Свойства ромба
1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Помимо этого:
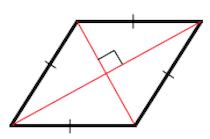
2. Диагонали ромба перпендикулярны.
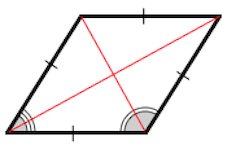
3. Диагонали ромба являются биссектрисами его углов.
4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Признаки ромба
Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:
1. Все стороны параллелограмма равны между собой ().
2. Диагонали пересекаются под прямым углом ().
3. Диагонали параллелограмма являются биссектрисами его углов.
Площадь ромба
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Ромб. Формулы, признаки и свойства ромба
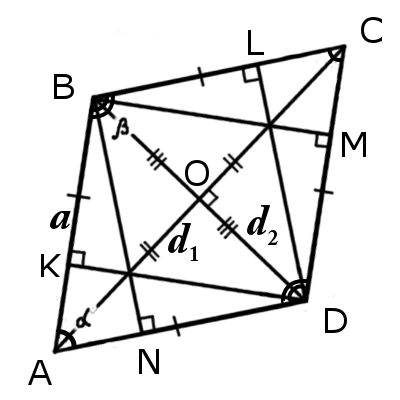 | 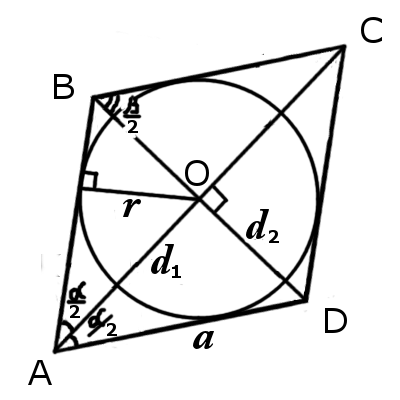 |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
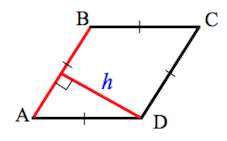
Сторона и высота ромба
Свойства
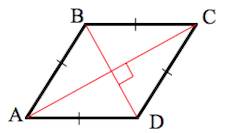
Ромб – это геометрическая фигура, у которой все стороны равны, поэтому ее периметр, как и периметр квадрата равен стороне, умноженной на 4. Площадь ромба зависит не только от его стороны, но и высоты, так как ромб является параллелограммом, эта формула заимствована от него. Чтобы вычислить площадь ромба необходимо умножить высоту на его сторону. P=4a S=ah
Углы ромба также связаны с высотой, так как она образует внутри ромба прямоугольный треугольник. Синус угла α в ромбе равен отношению высоты, как катета, к стороне ромба, как гипотенузе. Угол β можно найти через разность 180 градусов и угла α. (рис.115.1) sinα=h/a β=180°-α
Зная любой угол ромба, можно найти его диагонали. Поскольку диагонали ромба пересекаются под прямым углом, они делят ромб на четыре конгруэнтных прямоугольных треугольника, катетами которых являются половины диагоналей и гипотенузой – сторона ромба. Соответственно в каждом таком треугольнике, углы равны половинам углов ромба. Вычислить диагонали через угол α можно, приравняв их к стороне ромба умноженной на синус или косинус α соответственно. (рис.115.2) d_1=a sin〖α/2〗 d_1=a cos〖α/2〗
Так как ромб является равносторонним многоугольником, следовательно, в него можно вписать окружность. Радиус вписанной окружности соединяет ее центр в точке пересечения диагоналей и сторону ромба перпендикулярным ей отрезком. Поскольку единственным перпендикуляром в ромбе является высота, то в совокупности с вышеописанным свойствами можно сделать вывод, что радиус равен половине высоты ромба. (рис.115.3) r=h/2
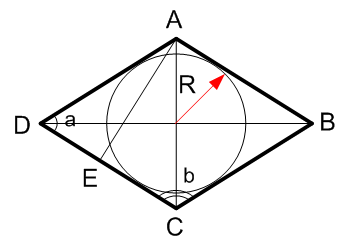
Что такое ромб: определение, свойства, признаки
В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
Определение ромба
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
Примечание: квадрат является частным случаем ромба.
Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
Свойство 2
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.
Формулы ромба
Для расчёта всех основных параметров ромба воспользуйтесь калькулятором.
Свойства ромба
Признаки ромба
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
Длина стороны ромба через площадь (S) и синус угла
Длина стороны ромба через диагонали
Длина стороны ромба через диагональ и угол
Длина стороны ромба через периметр
Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина диагонали ромба через сторону и другую диагональ
Длина диагонали ромба через площадь и другую диагональ
Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
Площадь ромба через сторону и синус любого угла
Площадь ромба через две диагонали
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
Радиус вписанного круга в ромб через площадь и сторону ромба
Радиус вписанного круга в ромб через сторону и синус любого угла
Радиус вписанного круга в ромб через диагональ и синус угла
Радиус вписанного круга в ромб через две диагонали