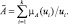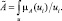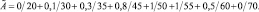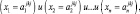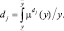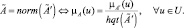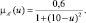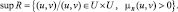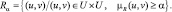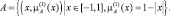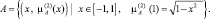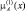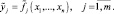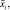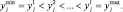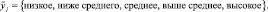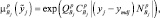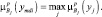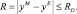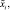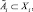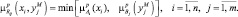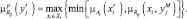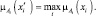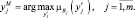что такое высота нечеткого множества

2.1. Определение и основные характеристики нечетких множеств

Нечеткое множество(fuzzyset) представляет собой совокупность элементов произвольной природы, относительно которых нельзя точно утверждать – обладают ли эти элементы некоторым характеристическим свойством, которое используется для задания нечеткого множества.

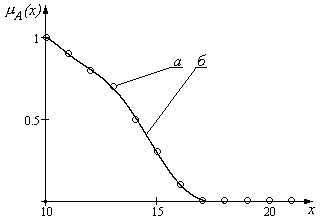
где знак суммирования обозначает не операцию арифметического сложения, а объединения элементов в одно множество. Носителем нечеткого множества A будет конечное подмножество (дискретный носитель):

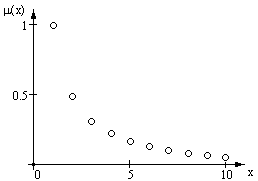
Рис.2.1. Функции принадлежности нечетких множеств с (а)-дискретным и (б)-непрерывным носителями

Рис.2.2. Графическое представление нечеткого множества малый

Пример. Нечеткое понятие «очень маленькое количество деталей» может быть представлено в виде конечного нечеткого множества который является конечным четким множеством. Нечеткое понятие «очень большое количество деталей» может быть представлено в виде нечеткого множества с бесконечным счетным носителем S A ≡ N (множество натуральных чисел), который имеет счетную мощность в обычном смысле.

Величина sup x ∈ X μ A x называется высотой нечеткого множества.

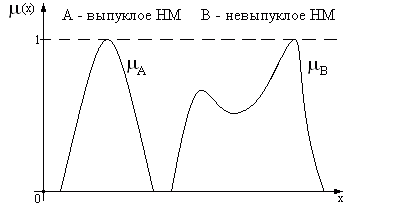
Рис.2.3. Функции принадлежности выпуклого и невыпуклого нечетких множеств

Источник

Нечеткие множества

где μ_А(х) —характеристическая функция, принимающая значе­ние 1, если х удовлетворяет свойству R, и 0 – в противном случае.

Нечеткое подмножество отличается от обычного тем, что для элементов х из Е нет однозначного ответа «да-нет» относительно свойства R. В связи с этим нечеткое подмножество А универсаль­ного множества Е определяется как множество упорядоченных пар

где μ_А(х) — характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве М (например, М = [0, 1]).

Функция принадлежности указывает степень (или уровень) принадлежности элемента х подмножеству А. Множество М назы­вают множеством принадлежностей. Если М = <0, 1>, то нечеткое подмножество А может рассматриваться как обычное или четкое множество.

Примеры записи нечеткого множества

Тогда А можно представить в виде

Замечание. Здесь знак «+» не является обозначением операции сложения, а имеет смысл объединения.

Основные характеристики нечетких множеств

Пусть М = [0, 1] и А — нечеткое множество с элементами из универсаль­ного множества Е и множеством принадлежностей М.

• Величина называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота рав­на 1,т.е. верхняя граница его функции принадлежности равна 1 ( = 1). При

• Нечеткое множество пусто, если ∀x ϵ E μ_A(x) = 0. Непу­стое субнормальное множество можно нормализовать по формуле

• Нечеткое множество унимодально, если μ_A(x) = 1 только на одном х из Е.

• Носителемнечеткого множества А является обычное под­множество со свойством μ_A(x)>0, т.е. носитель А = <x/x ϵ E, μ_A(x)>0>.

Примеры нечетких множеств

«Несколько» = 0,5/3 + 0,8/4 + 1/5 + 1/6 + 0,8/7 + 0,5/8; его характеристики: высота = 1, носитель = <3, 4, 5, 6, 7, 8>, точки перехода — <3, 8>.

2. Пусть Е = <0, 1, 2, 3,…, n,…>. Нечеткое множество «Малый» можно определить:

где х — возраст СИДОРОВА.

4. Пусть Е = <ЗАПОРОЖЕЦ, ЖИГУЛИ, МЕРСЕДЕС,… >– множе­ство марок автомобилей, а Е’ = [0, ∞] — универсальное множество «Сто­имость», тогда на Е’ мы можем определить нечеткие множества типа:

Рис. 1.1. Примеры функций принадлежности

«Для бедных», «Для среднего класса», «Престижные», с функциями при­надлежности вида рис. 1.1.

Имея эти функции и зная стоимости автомобилей из Е в данный момент времени, мы тем самым определим на Е’ нечеткие множества с этими же названиями.

Так, например, нечеткое множество «Для бедных», заданное на уни­версальном множестве Е = < ЗАПОРОЖЕЦ, ЖИГУЛИ, МЕРСЕДЕС. >, выглядит так, как показано на рис. 1.2.

Рис. 1.2. Пример задания нечеткого множества

Аналогично можно определить нечеткое множество «Скоростные», «Средние», «Тихоходные» и т. д.

5. Пусть Е — множество целых чисел:

Тогда нечеткое подмножество чисел, по абсолютной величине близких к нулю, можно определить, например, так:

О методах построения функций принадлежности нечет­ких множеств

В приведенных выше примерах использованы пря­мые методы, когда эксперт либо просто задает для каждого х ϵ Е значение μ_А(х), либо определяет функцию совместимости. Как правило, прямые методы задания функции принадлежности ис­пользуются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения.

Во многих задачах при характеристике объекта можно выде­лить набор признаков и для каждого из них определить полярные значения, соответствующие значениям функции принадлежности, 0 или 1.

Например, в задаче распознавания лиц можно выделить шкалы, приведенные в табл. 1.1.

Таблица 1.1. Шкалы в задаче распознавания лиц

При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкрет­ное лицо и каждый должен дать один из двух ответов: «этот че­ловек лысый» или «этот человек не лысый», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение μ_лысый (данного лица). (В этом примере можно действо­вать через функцию совместимости, но тогда придется считать число волосинок на голове у каждого из предъявленных эксперту лиц.)

На практике эксперт сам формирует матрицу А, при этом пред­полагается, что диагональные элементы равны 1, а для элемен­тов симметричных относительно диагонали a_ij= 1/a_ij, т.е. если один элемент оценивается в α раз сильнее, чем другой, то этот по­следний должен быть в 1/α раз сильнее, чем первый. В общем случае задача сводится к поиску вектора ω, удовлетворяющего уравнению вида Aw= λ_maxw, где λ_max— наибольшее собствен­ное значение матрицы А. Поскольку матрица А положительна по построению, решение данной задачи существует и является поло­жительным.

Можно отметить еще два подхода:

Источник

Научная электронная библиотека

Оразбаев Б. Б., Курмангазиева Л. Т., Коданова Ш. К.,

4.2. Моделирования в нечеткой среде на основе методов теории нечетких множеств

1. Основы теории нечетких множеств.

2. Методы построения нечетких моделей и нечеткое моделирование.

1. Основы теории нечетких множеств

Понятие нечеткого множества – эта попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать к данному множеству с различной степенью. При таком подходе высказывания типа «такой-то элемент принадлежит данному множеству» теряют смысл, поскольку необходимо указать «насколько сильно» или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.

Определение 1. Нечетким множеством (fuzzy set) на универсальном множестве U называется совокупность пар (μA(u), u), где μA(u) – степень принадлежности элемента u ∈ U к нечеткому множеству . Степень принадлежности – это число из диапазона [0,1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.

Определение 2. Функцией принадлежности (membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.

В случае непрерывного множества U используют такое обозначение

Примечание: знаки Σ и ∫ в этих формулах означают совокупность пар μA(u) и u.

Пример. Представить в виде нечеткого множества понятие «мужчина среднего роста».

Определение 3. Лингвистической переменной (linguistic variable) называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.

Определение 4. Терм-множеством (term set) называется множество всех возможных значений лингвистической переменной.

Определение 5. Термом (term) называется любой элемент терм–множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.

Пример. Рассмотрим переменную «скорость автомобиля», которая оценивается по шкале «низкая», «средняя», «высокая» и «очень высокая». В этом примере лингвистической переменной является «скорость автомобиля», термами – лингвистические оценки «низкая», «средняя», «высокая» и «очень высокая», которые и составляют терм–множество.

Определение 6. Дефаззификацией (defuzzification) называется процедура преобразования нечеткого множества в четкое число.

В теории нечетких множеств процедура дефаззификации аналогична нахождения характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности.

Для многоэкстремальных функций принадлежности в Fuzzy Logic Toolbox запрограммированы такие методы дефаззификации: Centroid – центр тяжести; Bisector – медиана; LOM (Largest Of Maximums) – наибольший из максимумов; SOM (Smallest Of Maximums) – наименьший из максимумов; Mom (Mean Of Maximums) – центр максимумов.

Определение 7. Нечеткой базой знаний (fuzzy knowledge base) о влиянии факторов Х = <х1, х2, …, хn>на значение параметра y называется совокупность логических высказываний типа:

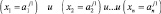
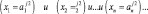
ЕСЛИ ИЛИ

ИЛИ

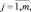
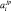
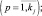
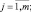
для всех где – нечеткий терм, которым оценивается переменная xi в строчке с номером jp kj – количество строчек-конъюнкций, в которых выход y оценивается нечетким термом dj, m – количество термов, используемых для лингвистической оценки выходного параметра y.

С помощью операций ∪ (ИЛИ) и ∩ (И) нечеткую базу знаний из определения 7 перепишем в более компактном виде:

(4.21)

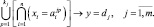
Определение 8. Нечетким логическим выводом (fuzzy logic inference) называется апроксимация зависимости y = f(x1, x2, …, xn) с помощью нечеткой базы знаний и операций над нечеткими множествами.

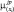
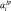
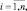
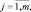
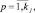
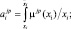
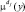
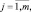
Пусть – функция принадлежности входа xi нечеткому терму ,
т.е. – функция принадлежности выхода y нечеткому терму dj, т.е.

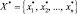
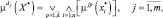
Тогда степень принадлежности конкретного входного вектора нечетким термам dj из базы знаний (4.21) определяется следующей системой нечетких логических уравнений:

(4.22)

где ∨(∧) – операция максимума (минимума).

Нечеткое множество , соответствующее входному вектору x*, определяется следующим образом:

(4.23)

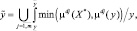
где U – операция объединения нечетких множеств.

Четкое значение выхода y, соответствующее входному вектору x* определяется в результате деффаззификации нечеткого .

Свойства нечетких множеств

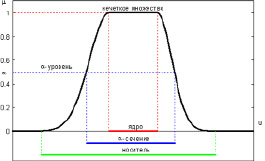
Определение 9. Высотой нечеткого множества называется верхняя граница его функции принадлежности: Для дискретного универсального множества U супремум становится максимумом, а значит высотой нечеткого множества будет максимум степеней принадлежности его элементов

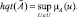
Определение 10. Нечеткое множество называется нормальным, если его высота равна единице. Нечеткие множества, не являющиеся нормальными, называются субнормальными. Нормализация – преобразование субнормального нечеткого множества в нормальное определяется так:

В качестве примера на рис. 4.2 показана нормализация нечеткого множества с функцией принадлежности

Рис. 4.2. Нормализация нечеткого множества

Рис. 4.2 иллюстрирует определения носителя, ядра, α-сечения и α-уровня нечеткого множества.

Определение 11. Носителем нечеткого множества называется четкое подмножество универсального множества U, элементы которого имеют ненулевые степени принадлежности: (рис. 4.3).

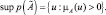
Определение 12. Нечеткое множество называется пустым, если его носитель является пустым множеством.

Определение 13. Ядром нечеткого множества называется четкое подмножество универсального множества U, элементы которого имеют степени принадлежности равные единице: (рис. 4.3). Ядро субнормального нечеткого множества пустое.

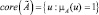
Определение 14. α-сечением (или множеством α-уровня) нечеткого множества называется четкое подмножество универсального множества U, элементы которого имеют степени принадлежности большие или равные α: α ∈ [0, 1] (рис. 4.3). Значение α называют α-уровнем. Носитель (ядро) можно рассматривать как сечение нечеткого множества на нулевом (единичном) α-уровне.

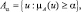
Определение 15. Нечеткое множество называется выпуклым если: u1, u2 ∈ U, λ ∈ [0, 1]. Альтернативное определение: нечеткое множество будет выпуклым, если все его α-сечения – выпуклые множества. На рис. 4.4 приведены примеры выпуклого и невыпуклого нечетких множеств.

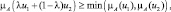
Рис. 4.3. Ядро, носитель и α-сечение нечеткого множества

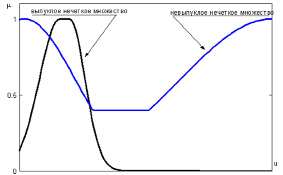
Определение 16. Нечеткие множества и равны если μA(u) = μB(u), ∀u ∈ U.

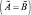
Универсальное множество U можно описать функцией принадлежности вида μU (u) = 1, ∀u ∈ U.

Рис. 4.4. К определению выпуклого нечеткого множества

Нечетким отношением R на множестве U называют нечеткое подмножество декартова произведения U×U, которое характеризуется функцией принадлежности μR:U×U → [0, 1] (μR:U×U → L). Значение μR(u, u) этой функции понимается как некоторая субъективная мера выполнения отношения uRu (L – некоторая произвольная решетка).

Очевидно, что, как в случае нечетких множеств, обычное отношение можно рассматривать как частный случай нечеткого отношения, функция принадлежности которого понимает значения 0 или 1.

Дадим некоторые определения, характеризующие нечеткие отношения.

Носителем нечеткого отношения R на множестве U называют подмножество декартова произведения U×U вида

Носитель нечеткого отношения следует понимать как отношение на множестве U, связывающие все пары (u, v), для которых степень выполнения данного нечеткого отношения не равна нулю.

По аналогии с нечеткими множествами определяется и множество уровня α нечеткого отношения, т.е.

Пример. Определим нечеткое множество чисел, «близких к нулю» на интервале [–1,1]. Это можно сделать различным образом в зависимости от выбора вида функции принадлежности. Очевидно, чем меньше расстояние от произвольной точки х до точки нуль, тем «больше шансов» у него быть элементом такого нечеткого множества. Такое нечеткое множество можно определить, например, так:

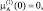
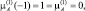
В этом случае при х = 0 имеем наибольшую функцию принадлежности а граничные точки хуже остальных удовлетворяют поставленному условию, так как что соответствует смыслу, который вкладывается в понятие таких чисел в математике.

Нечеткое множество А может быть определено с помощью функции принадлежности другого вида:

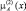
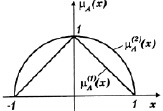
Функция тоже описывает н.м. чисел, «близких нулю». Наибольшее значение функции принадлежности достигается, как и в предыдущем случае, при x = 0. По мере отдаления от точки 0 значение функции принадлежности уменьшаются, а наименьшее ее значение (равные нулю) имеют граничные точки интервала [–1, 1].

На рис. 4.5 показаны графики функций принадлежности
и .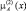

2. Методы построения нечетких моделей и нечеткое моделирование

2.1. Методы моделирования производственных объектов в нечеткой среде

Для качественного анализа реальных объектов и систем нужны подходы, для которых высокая точность и строгость математического формализма не является чем-то абсолютно необходимым и в которых используется методологическая схема, допускающая нечёткости и частичные истины. Существуют следующие подходы и методы моделирования объектов, удовлетворяющие этим требованиям, которые основаны на методах теории нечётких множеств.

1. Методы, основанные на построении статистических моделей объектов с нечёткими коэффициентами на основе методов регрессионного анализа. Модели, полученные на основе такого подхода, успешно используются при моделировании и управлении рядом технологических объектов нефтеперерабатывающей промышленности.

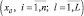
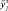
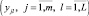
Предположим, что в результате наблюдения объекта или проведённого эксперимента получено L x1 , а соответствующие нечёткие значения выходных параметров оценены экспертами.

Для построения математической модели этого объекта необходимо решить следующие два этапа задачи идентификации:

а) Выбрать структуру функции (структурная идентификация)

(4.24)

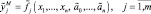
На этом этапе определяющее значение имеет качественный анализ объекта, в результате которого выявляются основные параметры, влияющие на функционирование, их взаимосвязи и выбирается метод для идентификации структуры модели.

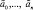
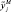
б) Определить оценки параметров выбранной функции (4.24) (параметрическая идентификация), например значений нечётких коэффициентов . Для подобной оценки можно воспользоваться критерием минимизации отклонения нечётких значений выходного параметра ,
полученных по модели (4.24), от его выборочных нечётких значений, полученных на основе экспертной оценки :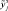

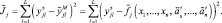
(4.25)

На втором этапе основным вопросом является выбор способа оценивания неизвестных параметров, обеспечивающего необходимые свойства исследуемого объекта.

В общем случае нечёткие модели, получаемые на основе этого подхода, имеют вид нечёткого уравнения множественной регрессии.

(4.26)

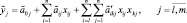
Использование понятия множество уровня α позволяет свести нечёткие уравнения регрессии к системе обычных уравнений регрессии. Такой подход даёт возможность применения классических методов регрессии для решения рассмотренных выше задач.

2. Методы, основанные на использовании логических правил условного вывода, например, в следующем виде:

(4.27)

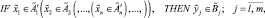
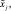
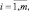
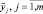
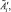
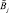
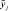
где – соответственно, входные и выходные, лингвистические переменные объекта, – нечёткие подмножества, характеризующие .

Преимуществом такого подхода является возможность его использования при моделировании объектов, для которых сбор статистической информации стоит очень дорого, затруднён или невозможен. В этом случае полученные нечёткие модели являются результатом обработки экспертного опроса специалистов-экспертов, оперирующих, как правило, информацией качественного характера (знания, опыт специалистов-экспертов, ЛПР). Такая информация, при условии достаточной компетенции специалистов-экспертов, позволяет в полученных моделях учесть всю гамму сложных внутренних взаимосвязей параметров объекта.

К достоинствам методов построения нечётких моделей можно отнести: они позволяют получить эффективные модели объекта в условиях неопределённости, когда традиционные подходы не дают существенных результатов. В моделях полученных на основе этих подходов учитываются внутренние связи основных параметров системы, которые не подлежат формализации. Однако, при построении нечётких моделей возникают свои специфические проблемы, например, связанные с проведением экспертного опроса, построением функции принадлежности нечётких параметров, определением структуры условного логического вывода и т.д.

2.2. Алгоритмы синтеза моделей в нечеткой среде

Алгоритм синтеза моделей в нечеткой среде при количественно измеримых входных параметрах и нечетких (качественных) выходных параметрах.

Перейдем к рассмотрению вопросов алгоритмизации методов нечеткого моделирования сложных комплексов технологических агрегатов, химико-технологических систем.

Предлагаем следующий алгоритм синтеза нечетких моделей, реализующий идея 1-го подхода к моделированию количественно трудноописываемых объектов, когда входные параметры четкие (измеримые), а выходные параметры – нечеткие, оцениваются специалистами-экспертами.

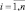
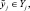
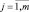
1. Выбрать необходимые для построения модели входные xi ∈ Xi, и выходные параметры технологического объекта.

2. Провести сбор информации и на основе экспертной процедуры, определить терм-множество нечетких параметров, описывающее состояние объекта.

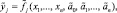
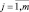
3. Определить структуру нечетких уравнений множественной регрессии (решение задачи структурной идентификации).

4. Построить функцию принадлежности нечетких параметров объекта и коэффициентов модели.

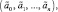
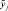
5. Оценить нечеткие коэффициенты выбранных функций (решение задачи параметрической идентификации)

6. Проверить соответствие модели реальным данным (адекватность модели). В случае неадекватности модели выяснить причину и вернуться к соответствующему пункту.

Этот алгоритм соответствует первому подходу моделирования нечетких объектов. Дадим пояснения к некоторым пунктам приведенного алгоритма.

В первом пункте в зависимости от требуемой точности выбираются наиболее информативные переменные, которые характеризует качество работы объекта. Для удобства диапазоны изменения нечетко описываемых параметров задаются в виде отрезков, с указанием минимального (ymin) и максимального значения (ymax). Эти отрезки в зависимости обсуждения специалистов-экспертов, разбиваются на несколько интервалов дискретизации (кванты), например:

Для построения терм-множества состояний (пункт 2) каждый квант выбранных параметров словесно характеризуется соответствующими нечеткими терминами. Например, если 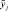– качество вырабатываемых продуктов на технологическом объекте, то их можно описать через термы:

Принятое терм-множество является совокупностью значений лингвистических переменных, описывающих работу исследуемого объекта. Каждый интервал дискретизации, получаемый в пункте 1, характеризуется определенным термом, этому терму соответствует нечеткое множество, которое описывается функцией принадлежности на соответствующем ей уровне градации.

Определение структуры нечетких уравнений множественной регрессии (пункт 3) и идентификация их нечетких коэффициентов (пункт 5) проводится в соответствии с этапами 1 и 2 приведенных выше в описании методов первой группы. Задача структурной идентификации решается по результатам системного анализа и исследования объекта, используя, например идею метода последовательного включения регрессоров, суть которого заключается в последовательном включении очередных регрессоров до выполнения условий адекватности модели к реальным данным. При параметрической идентификации можно использовать нечеткий аналог метода наименьших квадратов.

Построение функции принадлежности нечетких множеств (параметров) (пункт 4) является одним из основных этапов при моделировании сложных объектов с применением методов теории нечетких множеств. Основным способом восстановления этой функции является графическое построение кривой степени принадлежности того или иного параметра соответствующему нечеткому множеству. На основе полученного графика подбирается такой вид функции, который наилучшим образом аппроксимирует его. После этого идентифицируются параметры выбранной функции.

Предлагается следующая структура функции принадлежности:

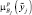
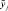
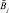
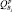
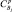
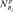
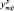
где – функция (степень) принадлежности параметров нечеткому множеству , характеризующая значения выходных параметров; p – номер градации (квота); – параметр, который находится при идентификации функции принадлежности и определяющий уровень нечеткости; ; – коэффициенты для изменения области определения термов и формы графика функции принадлежности нечетких параметров; – нечеткая переменная, наиболее соответствующая данному терму (в кванте p), для которой

Задачей заключительного этапа алгоритма (пункт 6) является проверка соответствия модели объекту (оригиналу). Модель считается адекватной (идентичной) моделируемому объекту, если найденные с ее помощью на компьютере характеристики объекта совпадают с заданной степенью точности с реальными данными, полученными экспериментально на самом объекте.

Как правило, в качестве критерия адекватности, являющегося мерой соответствия модели объекту, используется величина рассогласования расчетных (модельных) yM и реальных (экспериментальных) – yE данных; 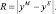Кроме того выбирается величина допустимого уровня рассогласования – RD. Модель считается адекватной, если

В случае неадекватности математическая модель дорабатывается, определяются источники неопределенности. Это может быть недооценка значимости какой-нибудь существенной переменной и недоучет ее в модели, неправильная или неполная структура нечетких уравнений, ошибка при параметрической идентификации и т.д. После этого осуществляется возврат к соответствующему пункту алгоритма для доработки модели.

Алгоритм моделирования производственных объектов при лингвистических входных и выходных параметрах

Следующий алгоритм реализует идею второго подхода, использующего логические правила условного вывода.

Некоторые пункты этого алгоритма (1, 2, 6) аналогичны соответствующим пунктам алгоритма НМ1, но учитывают нечеткость входных параметров – .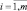

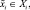
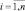
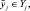
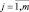
1. Выбрать необходимые для построения модели входные и выходные параметры объекта, которые являются лингвистическими переменными (Xi, Yj – универсальные множества);

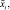
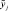
2. На основе экспертных оценок произвести оценку значений параметров и построить терм-множество T(Xi, Yj).

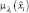
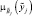
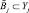
3. Построить функции принадлежности нечетких параметров – , ( – нечеткие подмножества ).

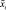
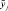
4. Построить лингвистическую модель объекта и формализовать нечеткие отображения Rij, определяющие связь между и .

5. Определить нечеткие значения выходных параметров объекта и выбрать их числовые значения из нечеткого множества решений.

6. Проверить условия адекватности модели. Если условие выполняется, модель рекомендуется для исследования и управления объектом, в противном случае вернуться к предыдущим пунктам для уточнения модели.

Рассмотрим некоторые детали описанного алгоритма.

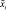
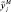
Лингвистическая (качественная) модель технологического объекта строится по результатам обработки экспертной информации (пункт 4). Для удобства ее можно оформить в виде таблицы, где словесно указаны различные значения входных параметров и соответствующие этим вариантам значения . Таблица должна заполняться с использованием выбранного в пункте 2 терм-множества. На основе модели, полученной таким образом, формализуются нечеткие отображения Rij, определяющие связь между входными и выходными факторами. Формализацию такого нечеткого отображения удобно осуществлять методом логической оценки. В этом случае на основе экспертной информации, используя экспертную информацию, используя терм-множества T(Xi, Yj) лингвистических переменных входа и выхода, дается полное описание всех возможных ситуаций. Это описание, которое называется лингвистической моделью, состоит из набора вложенных логических правил вида (4.27).

Нечеткие отображения для кванта p определяются как: .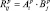
Для удобства применения нечеткого отображения Rij в расчетах нужно построить матрицы нечетких отношений – 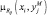, например, в общем случае для выделенных квантов:

Пятый пункт алгоритма синтеза нечетких моделей заключается в применении композиционного правила вывода:

где Ai ⊂ Xi, Bj ⊂ Yj, Xi, Yj – универсальные множества. С помощью этого правила можно осуществлять расчет выходных переменных, например, по следующему выражению (максиминное произведение):

Пусть 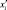– измеренные (оцененные экспертами) значения входных переменных, тогда искомое множество, которому принадлежат текущие измеряемые значения входных переменных, определяется как множество для которого измеряемые значения имеют наивысшую степень принадлежности:

Конкретные числовые значения выходных параметров 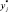из нечеткого множества решений определяются из следующего соотношения:

Заключение. В данном подразделе изложены основы теории нечетких множеств, даны основные определения и понятия теории нечетких множеств. Рассмотрены нечеткие и лингвистические переменные, нечеткая база знаний, нечеткий логический вывод, свойства нечетких множеств. Описаны методы моделирования производственных объектов в нечеткой среде. Предложены алгоритмы синтеза моделей в нечеткой среде; алгоритм синтеза моделей в нечеткой среде при количественно измеримых входных параметрах и нечетких (качественных) выходных параметрах и алгоритм моделирования производственных объектов при лингвистических входных и выходных параметрах.

1. Основы теории нечетких множеств.

2. Нечеткое множество, функция принадлежности.

3. Нечеткие и лингвистические переменные.

4. Нечеткая база знаний. Нечеткий логический вывод.

5. Нечеткое отношение.

6. Свойства нечетких множеств.

7. Методы моделирования производственных объектов в нечеткой среде.

8. Алгоритмы синтеза моделей в нечеткой среде.

9. Алгоритм синтеза моделей в нечеткой среде при количественно измеримых входных параметрах и нечетких (качественных) выходных параметрах.

10. Алгоритм моделирования производственных объектов при лингвистических входных и выходных параметрах.

Источник