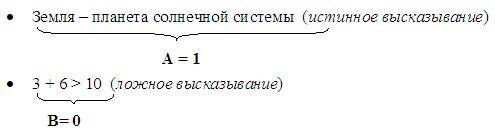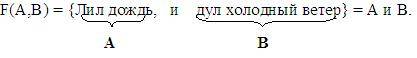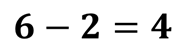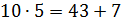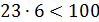что такое высказывание в алгебре логики

Алгебра высказываний

Алгебра высказываний

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)

Логическая переменная – это простое высказывание.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.

Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,

Многие люди не любят сырую погоду.

Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).

Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

Пример:
Рассмотрим составное высказывание «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.

2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
• в языках программирования — Or.
• Обозначение: \/, +, или, or.
• В алгебре множеств дизъюнкции соответствует операция объединения множеств.

Пример:
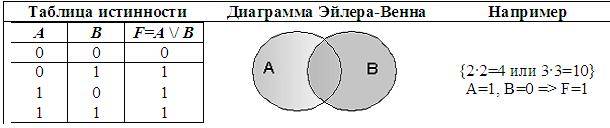
Рассмотрим составное высказывание «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.

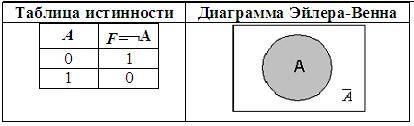
3. Отрицание (инверсия), от лат. InVersion – переворачиваю:

• Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
• в языках программирования — Not;
• Обозначение: не А, ¬А, not
• В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.

Источник

Основы алгебры логики

Основные понятия и аксиомы алгебры логики. Простые и сложные высказывания.

Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами.

Примерами высказываний на естественном языке являются предложения: « Сегодня светит солнце » или « На Красной площади зимой 2007–2008 гг. заливали каток ». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта. Каждое высказывание несет значение « истина » или « ложь ».

Определение. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.

Это определение не является математически точным.

Более того, только на первый взгляд оно кажется удовлетворительным. Это определение породило много логических парадоксов.

Причина этого парадокса лежит в структуре построения указанного предложения : оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя, и, следовательно, устранены возникающие отсюда парадоксы.

Интересную задачу, содержащую парадокс, придумал знаменитый математик « Известно, что в некотором городе брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея? »

Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.

Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание: « Крокодилы летают » – является истинным, и с этим значением высказывания будем работать.

Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.

Употребляемые в русском языке связки « и », « или », « не », « если…, то… », « тогда и только тогда, когда … » позволяют из уже заданных высказываний строить новые, более « сложные » высказывания.

Определение. Сложное высказывание – это высказывание, которое состоит из двух или более простых высказываний, объединенных логическими связками.

В алгебре логики логическая операция полностью задается таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний, входящих в сложное высказывание.

Логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 11.

Тема — Алгебра логики. Таблицы истинности

Перечень вопросов, рассматриваемых в теме: высказывание, логическая переменная, логические операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция), логические выражения, предикаты и их множества истинности, таблицы истинности и их анализ.

Глоссарий по теме: импликация, эквиваленция, предикат, примеры законов алгебры логики.

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.174—197)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения:

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.

Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем. Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Например, предложение «Джордж Буль — основоположник алгебры логики» истинно, а «Солнце — спутник Земли» ложно.

Употребляемые в обычной речи логические связки «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным. Например, из двух простых высказываний (каких?) можно получить следующее составное высказывание: «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач». Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С).

Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». Для логических значений «истина» — «ложь» могут использоваться следующие обозначения: И — Л, true — false, да — нет, 1 — 0.

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

В алгебре логики имеется шесть логических операций. Из курса информатики 8—9 классов вам знакомы три из них:

— отрицание (инверсия, логическое НЕ)

Высказыванию ставится в соответствие новое высказывание, значение которого противоположно исходному.

— конъюнкция (логическое умножение, логическое И)

Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.

— дизъюнкция (логическое сложение, логическое ИЛИ)

Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.

Рассмотрим новые логические операции.

— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией (от лат. implicatio — сплетение, тесная связь) или логическим следованием.

Операция импликации обозначается символом и задается следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если…, то». Как правило, эту связку мы используем, когда хотим показать зависимость одного события от другого.

Импликацию можно заменить на выражение, использующее ранее изученные операции НЕ и ИЛИ:

— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.

Строгая дизъюнкция обозначается символоми задается следующей таблицей истинности:

В русском языке строгой дизъюнкции соответствует связка «либо». Например, в пословице «Либо пан, либо пропал», выполнение обоих условий одновременно невозможно. В отличие от обычной дизъюнкции в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдет только одно событие.

Строгую дизъюнкцию можно представить через базовые операции следующим образом:

Чтобы доказать это равенство, достаточно для всех возможных комбинаций и вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения для тех же исходных данных.

— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.

В логике эквиваленция обозначается символом и задается следующей таблицей истинности:

В разговорной речи эквивалентности соответствует связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».

Если посмотреть внимательно на таблицы истинности для двух последних логических операций, то можно заметить, что эквивалентность — это обратная операция для операции «исключающее ИЛИ», т. е.

Можно заменить эквивалентность выражением, которое включает только базовые логические операции:

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Для логического выражения справедливо:

При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:

Операции одного приоритета выполняются в порядке их следования, слева направо. Как в математике, скобки меняют порядок выполнения операций.

Дан фрагмент таблицы истинности выражения F.

Источник

Что такое высказывание в алгебре логики

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

1. Логические выражения и логические операции

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.

Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.

Существуют разные варианты обозначения истинности и ложности логических переменных:

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Введем перечисленные логические операции.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Источник

Элементы алгебры логики. Высказывание

Урок 5. Информатика 8 класс (ФГОС)

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Элементы алгебры логики. Высказывание»

Сегодня мы с вами познакомимся с таким разделом математики как алгебра логики. Также узнаем, что такое логические переменные и логические значения.

Для начала узнаем, что же такое алгебра. Алгебра – это раздел математики, который изучает уравнения, содержащие цифры и буквенные обозначения, представляющие величины, подлежащие определению.

Например, x + y = 6.. Это алгебраическое уравнение, которое содержит переменные x и y. Если одна из переменных будет известна, можно будет найти вторую. Само же слово «алгебра» происходит от арабского Al—jabr, что означает «найти неизвестное». Многое из того, что изучает алгебра, вы проходите в школе на уроках математики. Например, натуральные, целые и рациональные числа, многочлены, множества и многое другое.

То есть вы знакомитесь с такими разделами математики, как алгебра чисел, алгебра множеств и так далее.

Существует ещё и такой раздел математики как алгебра логики. Для информатики это очень важный раздел. Алгебра логики – это раздел математической логики, который изучает высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. То есть в этом разделе математики подразумевается только два значения – истинно или ложно.

Высказывание – это предложение на любом языке, содержание которого можно однозначно определить, как истинное или ложное.

Давайте разберёмся на примере некоторых предложений.

«Москва – столица России».

«Шесть минус два равно четыре».

По поводу этих предложений можно сказать с уверенностью, что они истинны.

А вот, например, предложение «Зайцы зимой впадают в спячку.» – ложно.

Все вышеперечисленные предложения являются высказываниями, так как можно однозначно сказать истинны они или ложны.

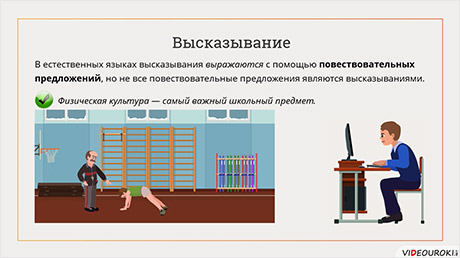
В естественных языках высказывания выражаются с помощью повествовательных предложений, но стоит помнить, что не все повествовательные предложения являются высказываниями. Например, предложение «Если попасть камнем в окно, то оно разобьётся.» не является высказыванием, так как нельзя однозначно сказать истинно оно или ложно.

Ведь в нём не уточняется какой камнем будет бросаться, маленький или большой, и с какой силой.

Или ещё одно предложение «Физическая культура – самый важный школьный предмет.» так же не относится к высказываниям, потому что для кого-то это важный предмет, так как ученик собирается дальше идти учится, например, на тренера, и соответственно для него это высказывание будет истинным. А вот для ученика, который планирует учиться на программиста, это высказывание будет ложным.

Но в тоже время предложение «Физкультура является очень полезным уроком.» будет являться истинным высказыванием, так как действительно, развитие интеллекта без физического здоровья будет неполноценный – так же, как и в обратном случае

Также стоит запомнить, что высказываниями не являются побудительные и вопросительные предложения. Например, «Сколько времени?», «Чей телефон звонит на уроке?», «Сколько тебя можно ждать!».

Для построения высказываний могут использоваться знаки различных формальных языков: математики, физики, химии и других.

Например, предложение «Гипотенуза прямоугольного треугольника находится по следующей формуле 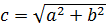.» является высказыванием, так как оно истинно.

Или же ещё одно «Формула воды в химии записывается так: H₂O.» также является высказыванием.

«Путь при равномерном прямолинейном движении находится по формуле ».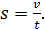

Это предложение является высказыванием, но высказыванием ложным, так как формула для нахождения пути при равномерном прямолинейном движении выглядит следующим образом: .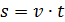

Числовые выражения не являются высказываниями. Но, в то же время, если из двух выражений составить одно и соединить их знаком равенства или неравенства, то новое выражение будет высказыванием. К примерам можно отнести следующие выражения:

Первое выражение истинно, так как 10 умноженное на 5 равно 50 и 43 плюс 7 также равно 50, соответственно они равны.

А вот второе ложно, так как 23, умноженное на 6, равно 138. Число 138 в свою очередь больше 100, а у нас стоит знак меньше.

Равенства или неравенства, которые содержат в себе переменные, также не относятся к высказываниям. Примерам будет являться неравенство x + y Оцените видеоурок

Источник