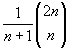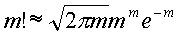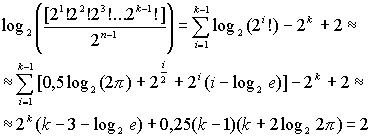что такое вырожденное дерево
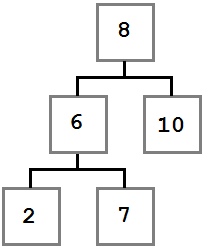
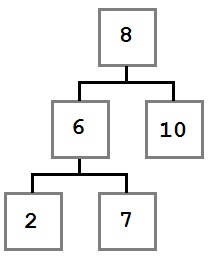
Что такое вырожденное дерево
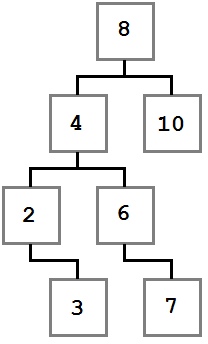
Рис.1. Примеры вырожденных деревьев
Идеальные деревья
Анализ ситуации основан на анализе последовательностей значений и на том, какие деревья порождаются последовательностями. Как известно, имеется n! различных последовательностей (перестановок) из n чисел. Это значительно больше, чем количество:
деревьев с n вершинами. Следовательно, некоторые перестановки порождают одинаковые деревья. В связи с единственностью идеального дерева вопрос должен быть сформулирован так: сколько различных последовательностей чисел при помещении этих чисел в бинарное дерево порождают идеальное дерево? Именно отношение числа таких последовательностей к общему числу различных последовательностей ( n! ) и характеризуют частоту появления идеальных деревьев.
Рис.2. Идеальное четырехуровневое дерево
Таким образом, общее количество вариантов построения последовательностей чисел, приводящих к идеальному графу при поуровневом заполнении, равно:
Два последних примера показывают, что идеальные деревья могут встречаться гораздо чаще, чем вырожденные. Чтобы показать, что для достаточно больших n это всегда так, оценим отношение частот их появления; причем частоту появления идеальных деревьев оценим снизу, используя количество последовательностей, строящих дерево по уровням. Чуть менее громоздко формула будет выглядеть, если взять логарифм отношения частот. Факториалы, встречающиеся в формулах, заменим приближенными выражениями по формуле Стирлинга:
Тогда логарифм отношения частот равен:
В выводе последней формулы для упрощения выражения некоторые конечные суммы (геометрической прогрессии и др.) заменены бесконечными, что, учитывая быструю сходимость соответствующих рядов, дает относительно небольшую ошибку.
Из этой формулы видно, что при k > 4 значение логарифма отношения частот положительно и, следовательно, идеальные деревья встречаются чаще вырожденных. Более того, значение логарифма быстро растет, увеличивая разрыв частот.
Из приведенных выше результатов можно с достаточной степенью уверенности сделать следующий вывод: хорошие деревья получаются в результате включения случайных элементов существенно чаще, чем плохие; поэтому, средние оценки сложности операций поиска и включения вероятнее всего будут логарифмическими.
B-tree
Введение
Деревья представляют собой структуры данных, в которых реализованы операции над динамическими множествами. Из таких операций хотелось бы выделить — поиск элемента, поиск минимального (максимального) элемента, вставка, удаление, переход к родителю, переход к ребенку. Таким образом, дерево может использоваться и как обыкновенный словарь, и как очередь с приоритетами.
Основные операции в деревьях выполняются за время пропорциональное его высоте. Сбалансированные деревья минимизируют свою высоту (к примеру, высота бинарного сбалансированного дерева с n узлами равна log n). Большинство знакомо с такими сбалансированными деревьями, как «красно-черное дерево», «AVL-дерево», «Декартово дерево», поэтому не будем углубляться.
В чем же проблема этих стандартных деревьев поиска? Рассмотрим огромную базу данных, представленную в виде одного из упомянутых деревьев. Очевидно, что мы не можем хранить всё это дерево в оперативной памяти => в ней храним лишь часть информации, остальное же хранится на стороннем носителе (допустим, на жестком диске, скорость доступа к которому гораздо медленнее). Такие деревья как красно-черное или Декартово будут требовать от нас log n обращений к стороннему носителю. При больших n это очень много. Как раз эту проблему и призваны решить B-деревья!
B-деревья также представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Но, в отличие от остальных деревьев, они созданы специально для эффективной работы с дисковой памятью (в предыдущем примере – сторонним носителем), а точнее — они минимизируют обращения типа ввода-вывода.
Структура
При построении B-дерева применяется фактор t, который называется минимальной степенью. Каждый узел, кроме корневого, должен иметь, как минимум t – 1, и не более 2t – 1 ключей. Обозначается n[x] – количество ключей в узле x.
Все листья B-дерева должны быть расположены на одной высоте, которая и является высотой дерева. Высота B-дерева с n ≥ 1 узлами и минимальной степенью t ≥ 2 не превышает logt(n+1). Это очень важное утверждение (почему – мы поймем чуть позже)!
h ≤ logt((n+1)/2) — логарифм по основанию t.
Операции, выполнимые с B-деревом
Как упоминалось выше, в B-дереве выполняются все стандартные операции по поиску, вставке, удалению и т.д.
Поиск
Операция поиска выполняется за время O(t logt n), где t – минимальная степень. Важно здесь, что дисковых операций мы совершаем всего лишь O(logt n)!
Добавление
В отличие от поиска, операция добавления существенно сложнее, чем в бинарном дереве, так как просто создать новый лист и вставить туда ключ нельзя, поскольку будут нарушаться свойства B-дерева. Также вставить ключ в уже заполненный лист невозможно => необходима операция разбиения узла на 2. Если лист был заполнен, то в нем находилось 2t-1 ключей => разбиваем на 2 по t-1, а средний элемент (для которого t-1 первых ключей меньше его, а t-1 последних больше) перемещается в родительский узел. Соответственно, если родительский узел также был заполнен – то нам опять приходится разбивать. И так далее до корня (если разбивается корень – то появляется новый корень и глубина дерева увеличивается). Как и в случае обычных бинарных деревьев, вставка осуществляется за один проход от корня к листу. На каждой итерации (в поисках позиции для нового ключа – от корня к листу) мы разбиваем все заполненные узлы, через которые проходим (в том числе лист). Таким образом, если в результате для вставки потребуется разбить какой-то узел – мы уверены в том, что его родитель не заполнен!
На рисунке ниже проиллюстрировано то же дерево, что и в поиске (t=3). Только теперь добавляем ключ «15». В поисках позиции для нового ключа мы натыкаемся на заполненный узел (7, 9, 11, 13, 16). Следуя алгоритму, разбиваем его – при этом «11» переходит в родительский узел, а исходный разбивается на 2. Далее ключ «15» вставляется во второй «отколовшийся» узел. Все свойства B-дерева сохраняются!
Операция добавления происходит также за время O(t logt n). Важно опять же, что дисковых операций мы выполняем всего лишь O(h), где h – высота дерева.
Удаление
Удаление ключа из B-дерева еще более громоздкий и сложный процесс, чем вставка. Это связано с тем, что удаление из внутреннего узла требует перестройки дерева в целом. Аналогично вставке необходимо проверять, что мы сохраняем свойства B-дерева, только в данном случае нужно отслеживать, когда ключей t-1 (то есть, если из этого узла удалить ключ – то узел не сможет существовать). Рассмотрим алгоритм удаления:
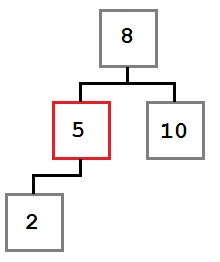
1)Если удаление происходит из листа, то необходимо проверить, сколько ключей находится в нем. Если больше t-1, то просто удаляем и больше ничего делать не нужно. Иначе, если существует соседний лист (находящийся рядом с ним и имеющий такого же родителя), который содержит больше t-1 ключа, то выберем ключ из этого соседа, который является разделителем между оставшимися ключами узла-соседа и исходного узла (то есть не больше всех из одной группы и не меньше всех из другой). Пусть это ключ k1. Выберем ключ k2 из узла-родителя, который является разделителем исходного узла и его соседа, который мы выбрали ранее. Удалим из исходного узла нужный ключ (который необходимо было удалить), спустим k2 в этот узел, а вместо k2 в узле-родителе поставим k1. Чтобы было понятнее ниже представлен рисунок (рис.1), где удаляется ключ «9». Если же все соседи нашего узла имеют по t-1 ключу. То мы объединяем его с каким-либо соседом, удаляем нужный ключ. И тот ключ из узла-родителя, который был разделителем для этих двух «бывших» соседей, переместим в наш новообразовавшийся узел (очевидно, он будет в нем медианой).
Рис. 1.
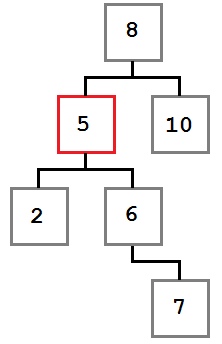
2)Теперь рассмотрим удаление из внутреннего узла x ключа k. Если дочерний узел, предшествующий ключу k содержит больше t-1 ключа, то находим k1 – предшественника k в поддереве этого узла. Удаляем его (рекурсивно запускаем наш алгоритм). Заменяем k в исходном узле на k1. Проделываем аналогичную работу, если дочерний узел, следующий за ключом k, имеет больше t-1 ключа. Если оба (следующий и предшествующий дочерние узлы) имеют по t-1 ключу, то объединяем этих детей, переносим в них k, а далее удаляем k из нового узла (рекурсивно запускаем наш алгоритм). Если сливаются 2 последних потомка корня – то они становятся корнем, а предыдущий корень освобождается. Ниже представлен рисунок (рис.2), где из корня удаляется «11» (случай, когда у следующего узла больше t-1 ребенка).
Рис.2.
Операция удаления происходит за такое же время, что и вставка O(t logt n). Да и дисковых операций требуется всего лишь O(h), где h – высота дерева.
Итак, мы убедились в том, что B-дерево является быстрой структурой данных (наряду с такими, как красно-черное, АВЛ). И еще одно важное свойство, которое мы получили, рассмотрев стандартные операции, – автоматическое поддержание свойства сбалансированности – заметим, что мы нигде не балансируем его специально.
Базы Данных
Проанализировав, вместе со скоростью выполнения, количество проведенных операций с дисковой памятью, мы можем сказать, что B-дерево несомненно является более выгодной структурой данных для случаев, когда мы имеем большой объем информации.
Очевидно, увеличивая t (минимальную степень), мы увеличиваем ветвление нашего дерева, а следовательно уменьшаем высоту! Какое же t выбрать? — Выбираем согласно размеру оперативной памяти, доступной нам (т.е. сколько ключей мы можем единовременно просматривать). Обычно это число находится в пределах от 50 до 2000. Разберёмся, что же дает нам ветвистость дерева на стандартном примере, который используется во всех статьях про B-tree. Пусть у нас есть миллиард ключей, и t=1001. Тогда нам потребуется всего лишь 3 дисковые операции для поиска любого ключа! При этом учитываем, что корень мы можем хранить постоянно. Теперь видно, на сколько это мало!
Также, мы читаем не отдельные данные с разных мест, а целыми блоками. Перемещая узел дерева в оперативную память, мы перемещаем выделенный блок последовательной памяти, поэтому эта операция достаточно быстро работает.
Соответственно, мы имеем минимальную нагрузку на сервер, и при этом малое время ожидания. Эти и другие описанные преимущества позволили B-деревьям стать основой для индексов, базирующихся на деревьях в СУБД.
Бинарные деревья поиска и рекурсия – это просто
Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.

Рис. 1 Бинарное дерево
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.

Рис. 2 Бинарное дерево поиска
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.

Рис. 3 Сбалансированное бинарное дерево поиска
Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.

Рис. 4 Экстремально несбалансированное бинарное дерево поиска
Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).
Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.
Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).
Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.
С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.
Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.
DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).
Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.
Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.

Рис. 5 Вспомогательный рисунок для обходов
Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.
Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение банкета статьи.
Алгоритмы и структуры данных для начинающих: двоичное дерево поиска
Авторизуйтесь
Алгоритмы и структуры данных для начинающих: двоичное дерево поиска
До сих пор мы рассматривали структуры данных, данные в которых располагаются линейно. В связном списке — от первого узла к единственному последнему. В динамическом массиве — в виде непрерывного блока.
В этой части мы рассмотрим совершенно новую структуру данных — дерево. А точнее, двоичное (бинарное) дерево поиска (binary search tree). Бинарное дерево поиска имеет структуру дерева, но элементы в нем расположены по определенным правилам.
3–5 декабря, Онлайн, Беcплатно
Для начала мы рассмотрим обычное дерево.
Деревья
Дерево — это структура, в которой у каждого узла может быть ноль или более подузлов — «детей». Например, дерево может выглядеть так:
Это дерево показывает структуру компании. Узлы представляют людей или подразделения, линии — связи и отношения. Дерево — это самый эффективный способ представления и хранения такой информации.
Дерево на картинке выше очень простое. Оно отражает только отношение родства категорий, но не накладывает никаких ограничений на свою структуру. У генерального директора может быть как один непосредственный подчиненный, так и несколько или ни одного. На рисунке отдел продаж находится левее отдела маркетинга, но порядок на самом деле не имеет значения. Единственное ограничение дерева — каждый узел может иметь не более одного родителя. Самый верхний узел (совет директоров, в нашем случае) родителя не имеет. Этот узел называется «корневым», или «корнем».
Вопросы о деревьях задают даже на собеседовании в Apple.
Двоичное дерево поиска
Двоичное дерево поиска похоже на дерево из примера выше, но строится по определенным правилам:
Давайте посмотрим на дерево, построенное по этим правилам:
Двоичное дерево поиска
Обратите внимание, как указанные ограничения влияют на структуру дерева. Каждое значение слева от корня (8) меньше восьми, каждое значение справа — больше либо равно корню. Это правило применимо к любому узлу дерева.
Учитывая это, давайте представим, как можно построить такое дерево. Поскольку вначале дерево было пустым, первое добавленное значение — восьмерка — стало его корнем.
Рассмотрим подробнее первые шаги.
В первую очередь добавляется 8. Это значение становится корнем дерева. Затем мы добавляем 4. Поскольку 4 меньше 8, мы кладем ее в левого ребенка, согласно правилу 2. Поскольку у узла с восьмеркой нет детей слева, 4 становится единственным левым ребенком.
После этого мы добавляем 2. 2 меньше 8, поэтому идем налево. Так как слева уже есть значение, сравниваем его со вставляемым. 2 меньше 4, а у четверки нет детей слева, поэтому 2 становится левым ребенком 4.
Затем мы добавляем тройку. Она идет левее 8 и 4. Но так как 3 больше, чем 2, она становится правым ребенком 2, согласно третьему правилу.
Последовательное сравнение вставляемого значения с потенциальным родителем продолжается до тех пор, пока не будет найдено место для вставки, и повторяется для каждого вставляемого значения до тех пор, пока не будет построено все дерево целиком.
Класс BinaryTreeNode
Класс BinaryTreeNode представляет один узел двоичного дерева. Он содержит ссылки на левое и правое поддеревья (если поддерева нет, ссылка имеет значение null ), данные узла и метод IComparable.CompareTo для сравнения узлов. Он пригодится для определения, в какое поддерево должен идти данный узел. Как видите, класс BinaryTreeNode очень простой:
Класс BinaryTree
Кроме того, в классе есть ссылка на корневой узел дерева и поле с общим количеством узлов.
Метод Add
Добавление узла не представляет особой сложности. Оно становится еще проще, если решать эту задачу рекурсивно. Есть всего два случая, которые надо учесть:
Если дерево пустое, мы просто создаем новый узел и добавляем его в дерево. Во втором случае мы сравниваем переданное значение со значением в узле, начиная от корня. Если добавляемое значение меньше значения рассматриваемого узла, повторяем ту же процедуру для левого поддерева. В противном случае — для правого.
Метод Remove
Удаление узла из дерева — одна из тех операций, которые кажутся простыми, но на самом деле таят в себе немало подводных камней.
В целом, алгоритм удаления элемента выглядит так:
Первый шаг достаточно простой. Мы рассмотрим поиск узла в методе Contains ниже. После того, как мы нашли узел, который необходимо удалить, у нас возможны три случая.
Случай 1: У удаляемого узла нет правого ребенка.
В этом случае мы просто перемещаем левого ребенка (при его наличии) на место удаляемого узла. В результате дерево будет выглядеть так:
Случай 2: У удаляемого узла есть только правый ребенок, у которого, в свою очередь нет левого ребенка.
В этом случае нам надо переместить правого ребенка удаляемого узла (6) на его место. После удаления дерево будет выглядеть так:
Случай 3: У удаляемого узла есть первый ребенок, у которого есть левый ребенок.
В этом случае место удаляемого узла занимает крайний левый ребенок правого ребенка удаляемого узла.
Давайте посмотрим, почему это так. Мы знаем о поддереве, начинающемся с удаляемого узла следующее:
Мы дожны поместить на место удаляемого узел со значением, меньшим или равным любому узлу справа от него. Для этого нам необходимо найти наименьшее значение в правом поддереве. Поэтому мы берем крайний левый узел правого поддерева.
После удаления узла дерево будет выглядеть так:
Теперь, когда мы знаем, как удалять узлы, посмотрим на код, который реализует этот алгоритм.
Отметим, что метод FindWithParent (см. метод Contains ) возвращает найденный узел и его родителя, поскольку мы должны заменить левого или правого ребенка родителя удаляемого узла.
Мы, конечно, можем избежать этого, если будем хранить ссылку на родителя в каждом узле, но это увеличит расход памяти и сложность всех алгоритмов, несмотря на то, что ссылка на родительский узел используется только в одном.
Метод Contains
Метод Count
Метод Clear
Обход деревьев
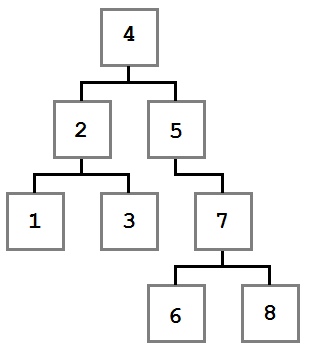
Обходы дерева — это семейство алгоритмов, которые позволяют обработать каждый узел в определенном порядке. Для всех алгоритмов обхода ниже в качестве примера будет использоваться следующее дерево:
Пример дерева для обхода
Также, кроме описания поведения и алгоритмической сложности метода будет указываться порядок значений, полученный при обходе.
Метод Preorder (или префиксный обход)
При префиксном обходе алгоритм получает значение текущего узла перед тем, как перейти сначала в левое поддерево, а затем в правое. Начиная от корня, сначала мы получим значение 4. Затем таким же образом обходятся левый ребенок и его дети, затем правый ребенок и все его дети.
Префиксный обход обычно применяется для копирования дерева с сохранением его структуры.
Метод Postorder (или постфиксный обход)
При постфиксном обходе мы посещаем левое поддерево, правое поддерево, а потом, после обхода всех детей, переходим к самому узлу.
Постфиксный обход часто используется для полного удаления дерева, так как в некоторых языках программирования необходимо убирать из памяти все узлы явно, или для удаления поддерева. Поскольку корень в данном случае обрабатывается последним, мы, таким образом, уменьшаем работу, необходимую для удаления узлов.
Метод Inorder (или инфиксный обход)
Инфиксный обход используется тогда, когда нам надо обойти дерево в порядке, соответствующем значениям узлов. В примере выше в дереве находятся числовые значения, поэтому мы обходим их от самого маленького до самого большого. То есть от левых поддеревьев к правым через корень.
В примере ниже показаны два способа инфиксного обхода. Первый — рекурсивный. Он выполняет указанное действие с каждым узлом. Второй использует стек и возвращает итератор для непосредственного перебора.
Метод GetEnumerator
Продолжение следует
На этом мы заканчивает пятую часть руководства по алгоритмам и структурам данных. В следующей статье мы рассмотрим множества (Set).