что такое выпуклый многоугольник простыми словами
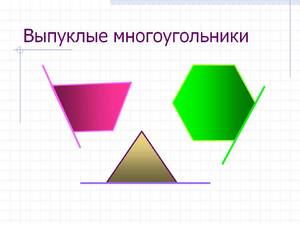
Выпуклый многоугольник
Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.
То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.
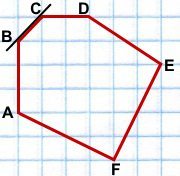
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.
2) MNKFEL — не выпуклый шестиугольник,
Он не лежит в одной полуплоскости относительно прямых KF и FE.
Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.
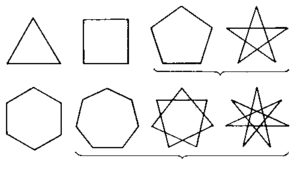
Важнейшие виды выпуклых многоугольников
Выпуклый многоугольник
Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Содержание
Определения
Существует множество эквивалентных определений:
Примеры
Вариации и обобщения
См. также
Полезное
Смотреть что такое «Выпуклый многоугольник» в других словарях:
выпуклый многоугольник — ▲ многоугольник ↑ выпуклый выпуклый многоугольник каждый внутренний угол меньше двух прямых; расположен в одной полуплоскости относительно любой прямой, содержащей его сторону. равносторонний. равноугольный многоугольник. изогон … Идеографический словарь русского языка
ВЫПУКЛЫЙ МНОГОУГОЛЬНИК — плоское выпуклое множество, граница к рого ломаная линия, состоящая из конечного числа прямолинейных отрезков. Иногда В. м. наз. только его границу. В. м. есть пересечение конечного числа (замкнутых) полуплоскостей. М … Математическая энциклопедия
Многоугольник — У этого термина существуют и другие значения, см. Многоугольник (значения). Примеры многоугольников Многоугольник это геометрическая фигура, обычно оп … Википедия
МНОГОУГОЛЬНИК — 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
Правильный многоугольник — выпуклый Многоугольник с равными сторонами и углами … Большая советская энциклопедия
Звёздчатый многоугольник — Звёздчатый многоугольник многоугольник, вершины которого расположены как у некоторого правильного многоугольника и стороны которого пересекаются между собой. Существует множество правильных звёздчатых многоугольников (или просто звёзд),… … Википедия
ПЛАНИГОН — выпуклый многоугольник правильного разбиения плоскости на равные многоугольники, т. е. такого разбиения, что существует группа движений плоскости, совмещающая разбиение с собой, к рая действует транзитивно на совокупности многоугольников… … Математическая энциклопедия
Вписанная окружность — Окружность, вписанная в многоугольник ABCDE Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектри … Википедия
Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями
Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.
Общие сведения
Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.
Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.
Любого вида многоугольник состоит из следующих частей:
Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.
Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.
Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.
А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.
Простейшие четырёхугольники
Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.
Наиболее часто приходится сталкиваться со следующими видами:
Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.
Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.
Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.
Треугольный многоугольник
Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.
В зависимости от особенностей, фигура может называться:
Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.
Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.
Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.
Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.
Теорема об углах
Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.
Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.
Геометрическая фигура многоугольник
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
Кроме того, принято различать следующие треугольники:
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>Выпуклый многоугольник
Связанные понятия
Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.
Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.
В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.
В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.
Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.
Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.