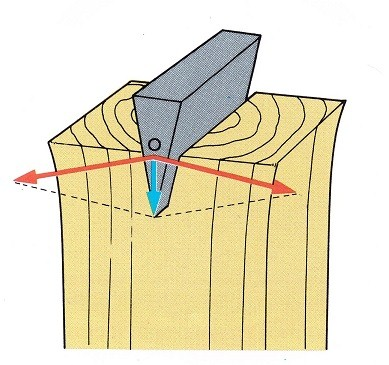
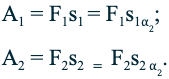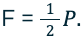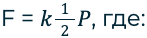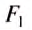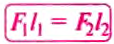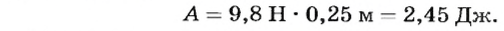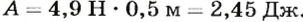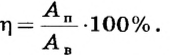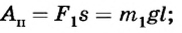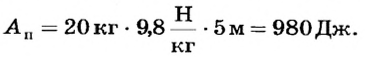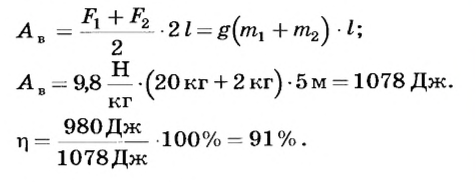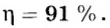что такое выигрыш в силе

Расчет выигрыша в силе: формула, примеры расчета с пояснениями

Содержание:

Рассмотрим, как рассчитать выигрыш в силе при использовании простейших механизмов, которые люди тысячелетиями используют для перемещения тяжёлых предметов: рычаги, наклонные поверхности, блоки. Первые применяются для перемещения массивных предметов с применением сил, которые имеют меньший за них вес; вторые – облегчают передвижение и подъём тел.

О простейших механизмах

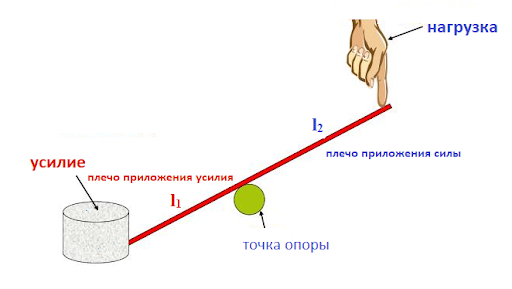
Части рычага до и после точки опоры называются плечами:

Механизм создаёт большее физическое усилие на коротком плече, чем сила, прилагаемая к длинному. На практике в его качестве применяются длинные (до нескольких метров) жёсткие деревянные балки, брус, металлические трубы.

Он же стал прообразом первых механических весов.

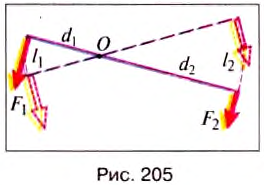
Рычаг будет находиться в равновесии до момента, пока вращающий его по часовой стрелке момент сил равняется силе, вращающей его в обратном направлении (по модулю). Если у механизма разные оси вращения – расстояние от точки опоры до места прикладывания усилия, такой рычаг даёт выигрыш в силе, расчёт которого проводится по формуле:

В данном случае l₁

Действительно, жёсткий рычаг с отличающейся в десятки раз длиной плеч сведёт к минимуму прикладываемую для передвижения либо подъёма предмета силу, но выигрыш в работе он не обеспечит. Во сколько раз легче будет подъем, ровно на столько вещь придётся переместить дальше, а значит выигрыша в работе не получить. Докажем это.

Выполняемая работа пропорциональна прикладываемой силе, пройденному телами расстоянию на угол поворота.

Отсюда выплывает, что энергия в системе ниоткуда не появляется и бесследно не исчезает, только переходит из одной формы в иную. Часть – уходит на нагрев тел вследствие их трения.

Примеры рычага: плоскогубцы, ножницы, клещи, ручной тормоз авто.

Какой выигрыш в силе дает подвижный блок

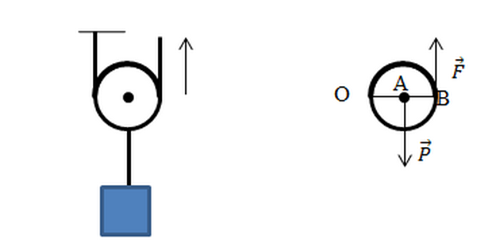
Различают неподвижные и подвижные блоки – колёса с продольными канавами для верёвки, крепящиеся на ось. Первые изменяют направление воздействия приложенной силы, не предоставляя преимуществ для перемещения вещей, вторые – прикладываемую силу. Подвижной блок перемещается с грузом, уменьшая прикладываемое для движения груза усилие.

Разберёмся, как найти выигрыш в силе в такой ситуации. Поднимая груз весом P посредством подвижного блока, нужно приложить вдвое меньшую силу, чем через неподвижный, ведь плечо OA (радиус) для силы P вдвое меньше OB (диаметра круга) для силы натяжения троса. Если тот вытягивается на длину l, груз поднимается только на половину этого расстояния l2:

С учётом силы трения формула расчета выигрыша в силе приобретает вид:

K – коэффициент трения.

Задача

Рабочий посредством подвижного блока поднимает ведро песка на высоту 6 м. При этом прилагается сила, равная 160 Н. Трение повышает прикладываемую силу на 10%. Рассчитать совершаемую человеком работу?

A = kFs=1,1*160*6= 1056 Дж 1,056 кДж.

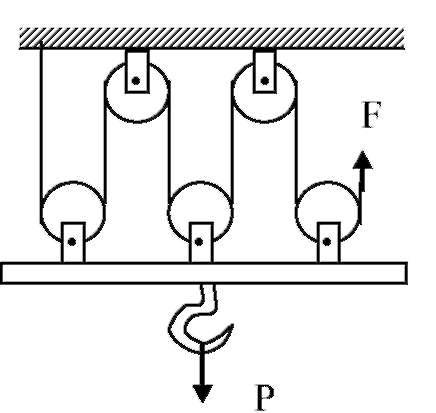
Какой выигрыш в силе даcт использование показанной на рисунке схемы?

Механизм представлен парой неподвижных и тремя подвижными блоками. Каждый снижает прикладываемую силу вдвое, даёт выигрыш в шесть раз.

Источник

Содержание:

Золотое правило механики:

Используя простые механизмы, можно изменять как силу, приложенную к телу, так и путь, от которого зависит значение работы. Означает ли это, что с помощью простых механизмов можно получить выигрыш в работе?

Теоретические сведения

Использование наклонной плоскости позволяет получить выигрыш в силе. Выигрыш в работе, как утверждает «золотое правило» механики, получить невозможно. В реальных условиях тот, кто пользуется наклонной плоскостью, даже проигрывает в работе, поскольку при перемещении тела но наклонной плоскости выполняется дополнительная работа по преодолению трения.

Золотое правило механики

Уравновесим рычаг, приложив к нему две разные по значению силы

Видим, что теперь в правиле рычага можно заменить отношение плечей сил на отношение путей точек приложения сил, тогда получим: 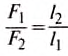Из свойства пропорции вытекает:

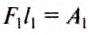
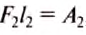
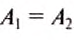
По определению механической работы: а , т. е. , отсюда делаем следующий вывод.

Рычаг выигрыша в работе не даёт.

Это касается и других простых механизмов.

Ни один из простых механизмов не даёт выигрыша в работе: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.

Это правило назвали «золотым правилом» механики.

Дает ли выигрыш в работе простой механизм

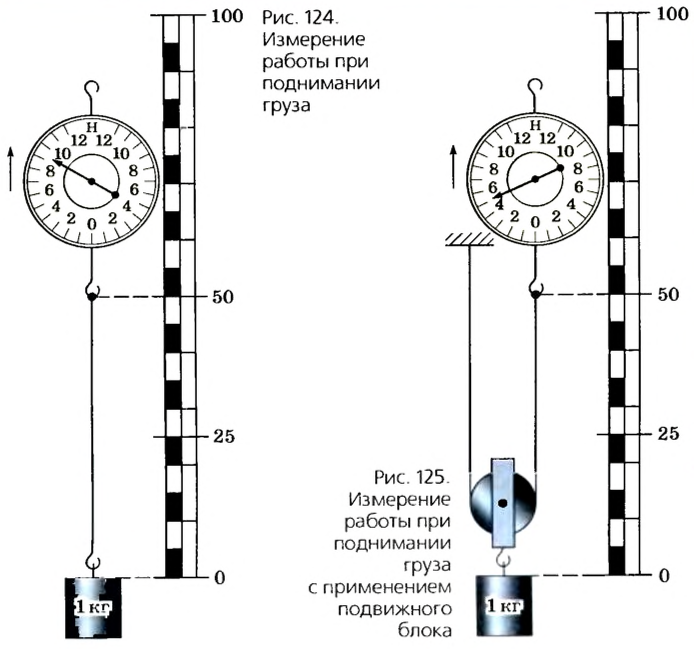
Закрепим конец нити на крючке динамометра и прикрепим к ней груз массой 1 кг (рис.124). Начнем равномерно поднимать его вверх. Динамометр покажет, что к нити приложена сила 9,8 Н. Поднимем груз на высоту 0,25 м и рассчитаем работу, которая при этом будет выполнена:

Конец нити закрепим неподвижно на штативе и пропустим ее через подвижный блок, к которому прикреплен груз массой 1 кг.

К свободному концу нити прикрепим динамометр и обозначим на линейке положение точки присоединения динамометра (рис. 125). Постепенно будем поднимать динамометр до тех пор, пока груз не переместится на 0,25 м. Динамометр при этом будет показывать силу 4,9 Н, но путь, который прошла точка присоединения динамометра, будет равен 0, 5 м. Выполненная работа в этом случае

Проанализировав результаты эксперимента, можно сделать вывод, что использовав подвижный блок, мы получили выигрыш в силе в 2 раза, но проиграли в пути, на котором действовала эта сила, тоже в 2 раза. Работа оказалась одинаковой и в первом, и во втором случае.

Итак, поднимать груз при помощи подвижного блока легче, чем без него. Однако путь, на котором действует сила, будет соответственно большим.

Никакого выигрыша в работе блок не дал. Подобное явление можно наблюдать и при использовании рычага и наклонной плоскости. Такая закономерность была замечена учеными еще в античные времена и выражена в «золотом правиле» механики.

При использовании простых механизмов оказывается, что при этом имеется даже некоторый проигрыш в работе. Так, выполняя работу с помощью простого механизма, нужно перемещать еще блок или рычаг, имеющих определенный вес, преодолевать силы трения. Эту работу нельзя назвать полезной.

Как оценить качество простого механизма

Чтобы оценить качество какого-либо простого механизма, сравнивают полезную работу, которую необходимо выполнить без этого механизма, с работой, которая выполняется с использованием простого механизма.

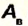
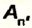
Число, показывающее, какую часть от всей выполненной работы составляет полезная работа называют коэффициентом полезного действия (КПД):

В формулах КПД обозначают греческой буквой 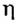(«эта»).

Коэффициент полезного действия удобно выражать в процентах. Тогда

Коэффициент полезного действия может иметь различные значения. Чем его значение больше, тем лучшим считается механизм. Но ни один исследователь или инженер не смог бы изготовить механизм с КПД большим или равным 100 %. И это не из-за несовершенства технологий. Просто этому мешают законы природы, которые человек не в силах изменить.

Таким образом, чтобы оценить качество механизма, необходимо сравнить выполненную и полезную работу.

Пример задачи с решением

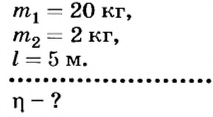
С помощью подвижного блока массой 2 кг на высоту 5 м подняли груз массой 20 кг. Определить коэффициент полезного действия установки.

Дано:

Решение

По определению

Полезная работа

Ответ.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Простые механизмы: что это такое, виды простых механизмов

Содержание:

Простые механизмы – это механические агрегаты, применяемые для направления силы либо её величины. Их называют дающими выигрыш в силе устройствами. Рассмотрим распространённые виды простых механизмов. Кратко коснёмся принципов их функционирования, приносимой пользы, целей применения.

Определение и разновидности

Из уроков истории известны факты применения приспособлений для метания снарядов, перемещения строительных материалов, передачи механической энергии. Они вызывали движения, преодолевающие большие силы, особенно противодействующие им в начале процесса, например, сдвигание тяжелого камня с места. Из предыдущих уроков вы знаете, что такое механическая работа. Она вычисляется как произведение приложенной к телу силы на преодолённое под её действием расстояние: A = F*s.

Природа создана так, что в замкнутой системе получить выигрыш в работе нельзя. Во сколько раз меньшую силу приложите, во столько проиграете в расстоянии – тело придётся перемещать дальше и наоборот. Простые механизмы применяют для того, чтобы развивать силы, равные по модулю и противоположные по значению противодействующим движению силам.

При расчётах величиной сил трения могут пренебрегать.

Простые механизмы в физике

Рычаг, как любой простой механизм, – преобразователь сил.

Блок – равноплечий рычаг. Представлен вращающимся колесом с желобком для верёвки по всей длине окружности. Неподвижный блок не даёт выигрыша в силе, а направляет её. Ось подвижного блока располагается в обоймах, двигается с ними, поэтому позволяет управлять силой. Для получения выигрыша также применяются сдвоенные блоки разного диаметра, насаженные на одну ось.

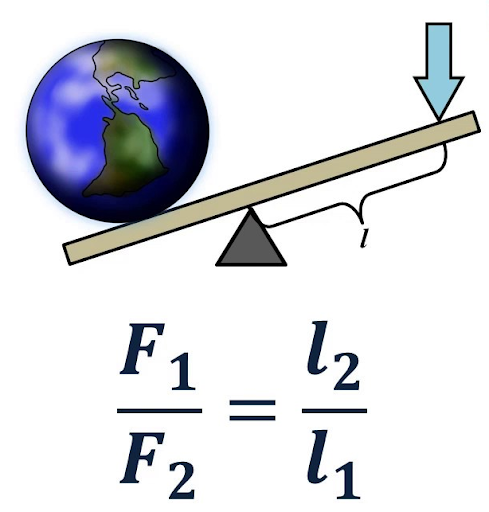
Ворот – модифицированный двойной блок, ранее применяемый для перетаскивания и подъёма грузов на небольшие расстояния либо высоты. В вороток вставляются длинные спицы, играющие роль большего блока, с радиусом большим, чем у меньшего блока.

В технике также применяют:

Распространены простые механизмы, такие как винт и клин. Пример клина – лезвие колуна. По тыльной стороне инструмента наносятся удары, например, кувалдой, и устройство погружается в древесину, раскалывая её. Чем меньше угол заточки лезвия, тем проще оно входит в дерево.

Клин применяется и для подъёма грузов. Особенность обоих видов клина – значительная сила трения, действующая между телом и боковыми гранями приспособления.

Винт работает по принципу клина, где вместо ударов совершается вращение крупного болта с малым шагом резьбы. Применяется в прессах, колунах, домкратах, при завинчивании крепежей (саморезов).

Примеры простых механизмов в повседневной жизни:

Какие простые механизмы вы знаете и используете в быту кроме названных? К какой категории отнести дверь в автомобиле, тиски, лебёдку?

Источник

Простые механизмы. Блок.

Одним из простых механизмов является блок. Блок — это колесо с желобом, по которому пропущена веревка или трос. Используется блок, как и все простые механизмы, для преобразования силы — т.е. изменения направления и модуля приложенной силы.

Блоки бывают подвижные и неподвижные. Рассмотрим каждый случай подробно.

Неподвижный блок.

Неподвижный блок — это блок, ось которого (точка О на рисунке) закреплена, и блок при подъеме грузов не опускается и не поднимается.

Такой блок можно рассматривать как рычаг первого рода, у которого оба плеча равны между собой, и равны радиусу колеса блока:

Так как плечи рычага равны, то мы не получим выигрыша в силе. Проверим это, используя формулу равновесия рычага:

В нашем случае неподвижного блока:

Действительно, для того чтобы уравновесить силу на одном конце веревки, перекинутой через блок, нам необходимо приложить такую же силу на другом конце. Поэтому неподвижные блоки используют в том случае, если удобнее изменить направление силы, для совершения работы. Например, удобнее поднимать груз, удерживая веревку при помощи своего веса, поэтому на рисунке экспериментатор использует неподвижный блок.

Используя комбинации из неподвижных блоков можно менять направление силы как угодно:

И в этом случае, используя уже два неподвижных блока — мы не получаем выигрыша в силе, зато изменили направление приложения силы, теперь для поднятия груза силу мы должны приложить в горизонтальном направлении.

Подвижный блок

Подвижный блок — это блок, ось которого не закреплена, а поднимается вместе с грузом. Изобразим подвижный блок находящийся в равновесии, отметим на рисунке силы, действующие на систему, а также плечи приложения этих сил:

Подвижный блок можно сравнить с рычагом второго рода. Действительно: точка опоры О лежит по одну сторону от точки приложения сил, отрезок ОА — плечо силы P

Источник

Учащиеся должны усвоить, что:

♦ простые механизмы — это устройства, которые облегчают совершение тяжелой работы, поскольку дают выигрыш в силе; к простым механизмам относятся рычаг, наклонная плоскость, блоки;

♦ выигрыш в силе — физическая величина, описывающая увеличение силы простым механизмом и равная отношению силы» с которой действует механизм на тело, к силе, с которой механизм приводится в действие: F/F_/;

♦ работа, совершаемая с помощью простого механизма, больше работы, совершаемой при непосредственном воздействии на тело;

♦ полезная работа — это работа силы, действующей на перемещаемое тело без использования механизма;

♦ полная или затраченная работа — работа силы по перемещению тела с использованием механизма;

♦ коэффициент полезного действия механизма — физическая величина, описывающая эффективность работы механизма и равная отношению полезной работы к затраченной, выраженному в процентах:

♦ КПД любого механизма меньше 1 или 100%.

Учащиеся должны научиться:

♦ «создавать» указанные понятия;

♦ устанавливать указанные факты;

♦ рассчитывать КПД механизма по определительной формуле.

Выигрыш в силе КПД

ПЗ 3в. Сравнить полезную А и затраченную работу А₁

Простые механизмы облегчают.

ПЗ 4. Какими величинами описать простые механизмы?

Для большинства механизмов F₁ A, но отличие может быть больше или меньше

Выигрыш в силе, F/F₁

Коэффициент полезного действия (КПД) η

А_п — полезная работа,

А₃ — затраченная работа

ОПРЕДЕЛЕНИЕ Выигрыш в силе — это.

ПЗ 5. Составить определение термина «простой механизм»

НАЗНАЧЕНИЕ Для облегчения совершения тяжелой работы в житейском понимании

ПРИНЦИП ДЕЙСТВИЯ Дают выигрыш в силе, изменяют направление силы

УСТРОЙСТВО Рычаг представляет собой.

Наклонная плоскость — это.

ОПРЕДЕЛЕНИЕ Простой механизм — это устройство, которое облегчает совершение работы, поскольку преобразует силу по направлению и/или модулю (дает выигрыш в силе)

Д/з. § 20, 23 (3, 4, 5), № 75, 76 (с. 143 учебника)

Этап актуализации знаний

П. Какие устройства изучили и что о них узнали?

У. (Вспоминают назначение простых механизмов, определения рычага, блока, наклонной плоскости, соотношение между силами и путями при непосредственном воздействии и с помощью механизмов.)

Этап «создания» нового знания

П. Вернемся к первоначальному вопросу, как отличается совершенная работа по подъему (опусканию) груза при непосредственном воздействии и с помощью простых механизмов. Запишите познавательную задачу Зв. Сравнить полезную А_п и затраченную А₃ работу. Что нужно сделать для получения ответа на этот вопрос?

У. Можно рассчитать для каждого механизма механическую работу А и А₁ по тем данным, которые есть, сравнить полученные значения и сделать вывод.

П. Приступайте к работе. У вас — 3 мин.

(Организует выполнение учащимися расчетов и выступления с результатами.) Что же мы видим? Используя механизмы, приходится совершать большую работу, чем без них. В чем же выгода от их использования?

У. Простые механизмы облегчают совершение работы, поскольку требуется меньшая сила для приведения их в действие, чем при непосредственном воздействии на тело, хотя работу приходится совершать большую.

П. Запишем этот результат. Итак, простые механизмы обладают привлекательным, выгодным свойством: увеличивают силу (усиливают) воздействия для совершения работы.

Простые механизмы обладают и огорчительным свойством: приходится выполнять большую работу.

Какими величинами целесообразно описывать эти свойства простых механизмов. Запишите познавательную задачу 4. Как решаются задачи такого типа?

У. Надо подобрать способ оценки свойства через известные величины, подобрать название и обозначить новую величину, составить формулу, установить ее единицу, составить определение

П. (Записывает на доске метод решения — см. «Вид доски».) Проанализируем еще раз результаты измерения сил. Для всех механизмов, кроме неподвижного блока, сила, приводящая его в действие, меньше силы тяжести груза. Но разница сил может быть больше или меньше. (Записывает.) Подумайте, как оценить эти различия. У вас — 1 мин.

У. Можно взять либо отношение сил F и F₁, либо их разность. Для выбора надо установить, какая из этих величин одинакова для разных значений сил F.

П. (Проводит опыт с подвижным блоком, подвесив больший груз.) Отношение остается таким же, как в первом опыте, а разность — другая. Значит, оценить изменение силы простым механизмом можно отношением сил F/F₁. Как бы вы назвали эту величину и как ее обозначили? (Выслушивает предложения учащихся.) Принято называть ее выигрышем в силе, говорят, что простой механизм дает выигрыш в силе в F/F₁ раз. Специального обозначения эта величина не имеет. Какова ее единица?

У. Это безразмерная величина.

П. Составьте определение выигрыша в силе. У вас — 1 мин на обдумывание.

У. Выигрыш в силе — это физическая величина, описывающая увеличение силы простым механизмом и равная отношению силы, с которой действует механизм на тело, к силе, с которой механизм приводится в действие: F/F₁.

П. Теперь обратимся к огорчительному свойству. У всех механизмов А₁ > А. Величины А и А₁ имеют специальные названия и обозначения. Откройте с. 60 учебника и выясните эти названия и обозначения. (Выслушивает ответы учащихся.) Запишем определения полезной и полной (затраченной) работы.

Затраченная работа при использовании любого механизма больше полезной. Однако у разных механизмов значения А и А₁ отличаются на разную величину. Чем меньше эти различия, тем лучше, эффективнее механизм. Как оценить эффективность механизма? Найдите соответствующую информацию в учебнике (с. 60, начиная с третьего абзаца). У вас — 5 мин.

У. Эффективность простого механизма характеризуют отношением Название этой величины — коэффициент полезного действия, или КПД. Обозначение η (греч. «эта»). Эта безразмерная величина, выражающаяся в процентах. Коэффициент полезного действия механизма — физическая величина, описывающая эффективность работы механизма и равная отношению полезной работы к полной, выраженному в процентах; 1, или 100% — это КПД такого механизма, у которого полезная и затраченная работы равны. КПД реальных механизмов меньше 1 или 100%.

Подведем итог. Почему выгодно использовать простые механизмы?

У. Простые механизмы позволяют с помощью малой силы человека получить большое по силе воздействие на тяжелые предметы для и перемещения или удержания в каком-то положении. И хотя пройденный путь оказывается больше, это выгодно, так как без механизма человек вообще не смог бы выполнить тяжелую работу.

П. Как мы это узнали?

У. Мы провели измерения и сравнили силы, действующие на тело, и проходимые пути без механизмов и с использованием механизмов, рассчитали и сравнили совершенную работу.

П. Давайте составим определение простого механизма. Запишите познавательную задачу 5. В определении технического устройства должно быть указано его назначение, принцип действия и основные части. (Записывает.) Подумайте и определите каждый из этих элементов. У вас — 2 мин.

У. (Дают определения простых механизмов.) Простой механизм — это устройство, которое служит для облегчения тяжелой работы, давая выигрыш в силе и/или изменяя направление воздействия.

Рычаг — простой механизм, представляющий собой твердое тело, которое может поворачиваться вокруг некоторой точки (оси).

Блок — простой механизм, представляющий собой укрепленное в обойме колесо с желобом, по которому пропущена веревка с незакрепленными на колесе или обойме концами. Блок называют неподвижным, если его ось закреплена и при движении веревки с грузом не перемещается. Блок называют подвижным, если при движении конца веревки колесо и обойма с грузом перемещаются.

Наклонная плоскость — простой механизм, представляющий собой твердое тело с плоской поверхностью, расположенной под углом к горизонту.

П. Как назвать сегодняшний урок? (Выслушивает учащихся.) Запишите тему перед познавательной задачей 3.

Демонстрация постоянства выигрыша в силе подвижного блока для разных значений веса поднимаемого груза.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник