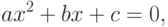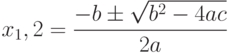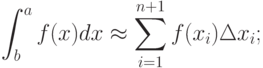что такое вычислительный эксперимент в информатике

Что такое вычислительный эксперимент

Информационное моделирование на компьютере

Основное преимущество компьютера перед человеком

Современным инструментом для информационного моделирования является компьютер. На компьютере можно писать тексты (строить вербальные модели), рисовать карты и схемы (графические модели), строить таблицы (табличные модели), но при таком использовании компьютера в моделировании его возможности проявляются не в полной мере.

Главное преимущество компьютера перед человеком — способность к быстрому счету. Современные компьютеры считают со скоростями в сотни тысяч, миллионы и даже миллиарды операций в секунду!

Для чего нужны математические модели

Многие процессы, происходящие в природе, в технике, в экономических и социальных системах, описываются сложными математическими соотношениями. Это могут быть уравнения, системы уравнений, системы неравенств и пр., которые являются математическими моделями описываемых процессов.

Математическая модель — это описание моделируемого процесса на языке математики.

Компьютерная математическая модель

Появление компьютеров сняло эти проблемы. Стало возможным проводить расчеты сложных математических моделей за приемлемое время. Например, рассчитать погоду на завтрашний день до его наступления. Ученые перестали себя ограничивать в сложности создаваемых математических моделей, полагаясь на быстродействие компьютеров.

Компьютерная математическая модель — это программа, реализующая расчеты состояния моделируемой системы по ее математической модели.

Что такое вычислительный эксперимент

Говорят также: «численный эксперимент».

Вычислительный эксперимент в некоторых случаях может заменить реальный физический эксперимент.

Важным свойством компьютерных математических моделей является возможность визуализации результатов расчетов. Этим целям служит использование компьютерной графики.

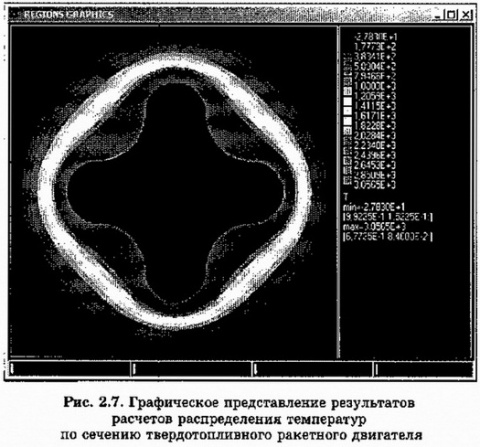
Представление результатов в наглядном виде — важнейшее условие для их лучшего понимания. Например, результаты расчетов распределения температуры в некотором объекте представляются в виде его разноцветного изображения: участки с самой высокой температурой окрашиваются в красный цвет, а в самой холодной — в синий. Участки с промежуточными значениями температуры окрашиваются в цвета спектра, равномерно переходящие от красного к синему (рис.2.7).

Для изображения изменяющихся со временем (динамических) результатов используют графическую анимацию.

Компьютерная графика позволяет человеку в процессе проведения численного эксперимента «заглянуть» в недоступные места исследуемого объекта. Можно получить изображение любого сечения объекта сложной формы с отображением рассчитываемых характеристик: температурных полей, давления и пр. В реальном физическом эксперименте такое можно сделать далеко не всегда. Например, невозможно выполнить измерения внутри работающей доменной печи или внутри звезды. А на модели это сделать можно.

Источник

Вычислительный эксперимент: определение, этапы и методы

Что такое вычислительный эксперимент, в этой статье мы будем разбираться с его этапами и отличительными чертами.

Что это?

Для начала приведем актуальные для научного мира определения вычислительного эксперимента:

Использование вычислительных экспериментов связано с изучением таких процессов, лабораторное или натурное исследование которых было затруднено или вовсе невозможно. Например, в 40-50-е годы прошлого века советский академик Келдыш М. В. разработал математическое описание полетов в космос.

Отличительные характеристики метода

Вычислительные эксперименты позволяют узнать то, что не подвластно классическим (лабораторной и натурной) методикам:

Лабораторный и натурный эксперименты

Чем же они отличны от моделирования, вычислительного эксперимента? Разницу можно осознать, ознакомившись с определениями:

Ключевые преимущества метода

Перечислим главные достоинства вычислительного эксперимента перед другими методиками:

Методы эксперимента

Перечислим основные методы вычислительного эксперимента:

Этапы

Проведение вычислительного эксперимента, как и любого другого исследования, начинается с постановки целей последующей работы:

А теперь предлагаем вам подробно разобрать каждый из этапов исследования.

Первый этап

Здесь первой главной задачей для ученого становится выбор из всего многообразия свойств объекта исследования тех, которые действительно необходимо изучить во время проведения эксперимента.

Далее для исследуемого процесса обязательно строится вычислительная (математическая) модель. Она создается так, что способна разделять все факторы, влияющие на объект эксперимента, на две группы:

Затем обязательно сформировать рамки применимости модели, до которых считаются справедливыми полученные результаты.

Второй этап

Третий этап

На этом шаге компьютерного вычислительного эксперимента создается программа, позволяющая реализовать составленный алгоритм. Это этап программирования для электронно-вычислительных устройств.

Фактически здесь создается проект подготовки кода, составленного на языке высокого уровня. Он будет реализацией алгоритма численного решения задач.

Здесь перед учеными возникают следующие проблемные вопросы:

Четвертый этап

На этой ступени проводятся расчеты непосредственно на ЭВМ. Надо сказать, данный этап во многом напоминает осуществление лабораторного эксперимента. Различие лишь одно: если в лаборатории ученые с помощью специально созданной установки задают свои вопросы природе, то здесь при помощи ЭВМ вопросы задаются уже математической модели.

Пятый этап

Вот мы и подошли к завершению вычислительного эксперимента. Здесь важно получить результаты расчета, представленные некоторой цифровой информацией, которая в дальнейшем нуждается в расшифровке.

Ученые переходят к проведению расчетов и анализу полученных результатов. Это требует не только значительных интеллектуальных усилий, но и достаточных навыков по представлению, обработке и переосмыслению имеющихся выводов:

Источник

Компьютерное моделирование и вычислительный эксперимент. Решение математических моделей

Компьютерное моделирование как новый метод научных исследований основывается на:

Вычислительный эксперимент позволяет заменить дорогостоящий натурный эксперимент расчетами на ЭВМ. Он позволяет в короткие сроки и без значительных материальных затрат осуществить исследование большого числа вариантов проектируемого объекта или процесса для различных режимов его эксплуатации, что значительно сокращает сроки разработки сложных систем и их внедрение в производство.

Компьютерное моделирование и вычислительный эксперимент как новый метод научного исследования заставляет совершенствовать математический аппарат, используемый при построении математических моделей, позволяет, используя математические методы, уточнять, усложнять математические модели. Наиболее перспективным для проведения вычислительного эксперимента является его использование для решения крупных научно-технических и социально-экономических проблем современности (проектирование реакторов для атомных электростанций, проектирование плотин и гидроэлектростанций, магнитогидродинамических преобразователей энергии, и в области экономики – составление сбалансированного плана для отрасли, региона, для страны и др.).

В некоторых процессах, где натурный эксперимент опасен для жизни и здоровья людей, вычислительный эксперимент является единственно возможным (термоядерный синтез, освоение космического пространства, проектирование и исследование химических и других производств).

Для проверки адекватности математической модели и реального объекта, процесса или системы результаты исследований на ЭВМ сравниваются с результатами эксперимента на опытном натурном образце. Результаты проверки используются для корректировки математической модели или решается вопрос о применимости построенной математической модели к проектированию либо исследованию заданных объектов, процессов или систем.

В заключение подчеркнем еще раз, что компьютерное моделирование и вычислительный эксперимент позволяют свести исследование «нематематического» объекта к решению математической задачи. Этим самым открывается возможность использования для его изучения хорошо разработанного математического аппарата в сочетании с мощной вычислительной техникой. На этом основано применение математики и ЭВМ для познания законов реального мира и их использования на практике.

В задачах проектирования или исследования поведения реальных объектов, процессов или систем математические модели, как правило, нелинейны, т.к. они должны отражать реальные физические нелинейные процессы, протекающие в них. При этом параметры (переменные) этих процессов связаны между собой физическими нелинейными законами. Поэтому в задачах проектирования или исследования поведения реальных объектов, процессов или систем чаще всего используются математические модели типа ДНА.

Согласно классификации приведенной в «лекции 1» :

Д – модель детерминированная, отсутствует (точнее не учитывается) влияние случайных процессов.

Н – модель непрерывная, информация и параметры непрерывны.

А – модель аналитическая, функционирование модели описывается в виде уравнений (линейных, нелинейных, систем уравнений, дифференциальных и интегральных уравнений).

Итак, мы построили математическую модель рассматриваемого объекта, процесса или системы, т.е. представили прикладную задачу как математическую. После этого наступает второй этап решения прикладной задачи – поиск или разработка метода решения сформулированной математической задачи. Метод должен быть удобным для его реализации на ЭВМ, обеспечивать необходимое качество решения.

Все методы решения математических задач можно разделить на 2 группы:

В точных методах решения математических задач ответ удается получить в виде формул.

Например, вычисление корней квадратного уравнения:

или, например, вычисление производных функций:

или вычисление определенного интеграла:

Однако, подставляя числа в формулу в виде конечных десятичных дробей, мы все равно получаем приближенные значения результата.

Для большинства задач, встречающихся на практике, точные методы решения или неизвестны, или дают очень громоздкие формулы. Однако, они не всегда являются необходимыми. Прикладную задачу можно считать практически решенной, если мы сумеем ее решить с нужной степенью точности.

Для решения таких задач разработаны численные методы, в которых решение сложных математических задач сводится к последовательному выполнению большого числа простых арифметических операций. Непосредственная разработка численных методов относится к вычислительной математике.

Примером численного метода является метод прямоугольников для приближенного интегрирования, не требующий вычисления первообразной для подынтегральной функции. Вместо интеграла вычисляется конечная квадратурная сумма:

x₁=a – нижний предел интегрирования;

x_n+1=b – верхний предел интегрирования;

n – число отрезков, на которые разбит интервал интегрирования (a,b) ;

– длина элементарного отрезка;

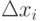
f(x_i) – значение подынтегральной функции на концах элементарных отрезков интегрирования.

Чем больше число отрезков n, на которые разбит интервал интегрирования, тем ближе приближенное решение к истинному, т.е. тем точнее результат.

Таким образом, в прикладных задачах и при применении точных методов решения, и при применении численных методов решения результаты вычислений носят приближенный характер. Важно только добиться того, чтобы ошибки укладывались в рамки требуемой точности.

Численные методы решения математических задач известны давно, еще до появления ЭВМ, но ими пользовались редко и только в сравнительно простых случаях в силу чрезвычайной трудоемкости вычислений. Широкое применение численных методов стало возможным благодаря ЭВМ.

Источник

Реферат по информатике на тему «Принципы проведения вычислительного эксперимента. Модель, алгоритм, программа»

Ищем педагогов в команду «Инфоурок»

ФГБОУ ВО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ

ИНСТИТУТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Кафедра информатики и вычислительной техники

Принципы проведения вычислительного эксперимента. Модель, алгоритм, программа

Автор работы: студентка 4 курса

группы МДМ-217 Старчкова Е.В.

Проверила: Кормилицина Т. В., канд. физ-мат. наук, доцент

1. Вычислительный эксперимент……………………………………….

2. Основные этапы вычислительного эксперимента……………………

3. Сферы применения вычислительного эксперимента и математического моделирования…………………………………….

4. Результаты расчёта последствий ядерного конфликта………………

Список использованной литературы………………………………………..

Ни одно техническое достижение не повлияло так на интеллектуальную деятельность че­ловека, как электронно-вычислительные машины. Увеличив в десятки и сотни миллионов раз скорость выполнения арифметических и логических операций, колоссально повысив тем самым производительность интеллектуального труда человека, ЭВМ вызвали коренные изменения в об­ласти обработки информации. По существу, мы являемся свидетелями своего рода “информационной революции”, подобной той промышленной революции, которую породило в 18 веке изобретение паровой машины и связанное с ним резкое повышение производительности физического труда. В настоящее время вычислительные машины проникают во все сферы интел­лектуальной деятельности человека, становятся одним из решающих факторов ускорения темпов научно-технического прогресса.

К концу 20 века компьютеры стали настолько совершенными, что появилась реальная воз­можность использовать их в научных исследованиях, не только как большой арифмометр, но об­ратиться с его помощью к изучению таких разделов математики, которые ранее были практически не доступны для исследований. Это было осознано при решении ещё на несовершенных ЭВМ сложных математических задач ядерной физики, баллистики, прикладной небесной механики.

Классическая математика, как известно, в основном нацелена на изучение явлений, имею­щих линейный характер, то есть способна изучать ситуации где причина приблизительно пропор­циональна следствию. Изменение причины приводит к пропорциональному изменению следст­вия, то есть классические уравнения рассматривают: не градиентные среды ( они изучают малые отклонения маятника, мелкие волны и дифференциал и т.д. )

После Второй Мировой Войны наука вплотную приблизилась к изучению явлений, яв­ляющихся не линейными, где причина и следствие не соизмеримы, именно благодаря таким явле­ниям возникли: электронные лампы, транзисторы, компьютеры, лазеры, появились высокоточные приборы способные избирать нужный сигнал, в большинстве случаев такие явления очень плохо поддаются традиционным методам анализа. Описывающие такие ситуации уравнения во многих случаях являются обыкновенными дифференциальными уравнениями, которые однако не имеют решения формами записи. Такие уравнения можно изучать и исследовать с помощью компьюте­ра.

К началу 70-х годов были обнаружены новые явления, а точнее на них обратили внимание, новые явления, которые ранее не предполагались. Оказалось, например, что возникающая в усло­виях землетрясения или резкого взрыва уединённая волна, получившая название “Саметон”, об­ладает удивительной устойчивостью. Это было смоделировано в численном эксперименте и на­блюдалось на практике. Математическая теория этого не линейного явления не была известна. Численные исследования позволили уяснить условия возникновения, распространения и свойства этого явления, этой волны. Другое важное открытие сделанное численным ( или вычислительным ) экспериментом это хаос в детерминированных ( описанных чёткой формулой ) системах, и хотя первые наблюдения таких явлений были выполнены ещё в начале 50-х годов, долгое время они рассматривались как несовершенство компьютеров, неспособных правильно вычислять. Изучение таких явлений, в ча­стности связанных с ними фракталов, привело к колоссальным сдвигам в со­временных научных представлениях. Возникла целая группа нелинейных наук, с которой связаны по истине удиви­тельные открытия последних лет.

1. Вычислительный эксперимент

Научное исследование реального процесса можно проводить теоретически или экспери­ментально, которые проводятся независимо друг от друга. Такой путь познания истины носит од­носторонний характер. В современных условиях развития науки и техники стараются проводить комплексное исследование объекта. Этого можно добиться на основе новой, удовлетворяющей требованиям времени, методологии и технологии научных исследований.

Широкое применение ЭВМ в математическом моделировании, достаточно мощная теоре­тическая и экспериментальная база позволяют говорить о вычислительном эксперименте как о новой технологии и методологии в научных и прикладных исследованиях.

Вычислительный эксперимент играет ту же роль, что и обыкновенный эксперимент при исследованиях новых гипотез. Современная гипотеза почти всегда имеет математическое описа­ние, над которым можно выполнять эксперименты.

При введении этого понятия следует особо выделить способность компьютера выполнять большой объем вычислений, реализующих математические исследования. Иначе говоря, компью­тер позволяет произвести замену физического, химического и т. д. эксперимента экспериментом вычислительным.

При проведении вычислительного эксперимента можно убедиться в необходимости и по­лезности последнего, особенно в случаях, когда провести натуральный эксперимент затрудни­тельно или невозможно. Вычислительный эксперимент, по сравнению с натурным, значительно дешевле и доступнее, его подготовка и проведение требует меньшего времени, его легко переде­лывать, он даёт более подробную информацию. Кроме того, в ходе вычислительного эксперимен­та выявляются границы применимости математической модели, которые позволяют прогнозиро­вать эксперимент в естественных условиях. Поэтому использование вычислительного экспери­мента ограничивается теми математическими моделями, которые участвуют в проведении иссле­дования. По этой причине вычислительный эксперимент не может заменить полностью экспери­мент натурный и выход из этого положения состоит в их разумном сочетании. В это случае в проведении сложного эксперимента используется широкий спектр математических моделей: пря­мые задачи, обратные задачи, оптимизированные задачи, задачи идентификации.

Использование вычислительного эксперимента как средства решения сложных приклад­ных проблем имеет в случае каждой конкретной задачи и каждого конкретного научного коллек­тива свои специфические особенности. И тем не менее всегда чётко просматриваются общие ха­рактерные основные черты, позволяющие говорить о единой структуре этого процесса. В на­стоящее время технологический цикл вычислительного эксперимента принято подразделять на ряд технологических этапов. И хотя такое деление в значительной степени условно, тем не менее оно позволяет лучше понять существо этого метода проведения теоретических исследований. Те­перь давайте рассмотрим основные этапы вычислительного эксперимента.

2. Основные этапы вычислительного эксперимента

В общем случае, основные этапы решения задачи с применением ЭВМ можно рассматри­вать как один технологический цикл вычислительного эксперимента. А вообще, вычислительный эксперимент как новая методика исследования «состоялся» после того, как удалось на каждом из этапов традиционной цепочки эффективно использовать вычислительную машину.

Теперь основные этапы вычислительного эксперимента:

· Проведение натурного эксперимента

· Построение математической модели

· Выбор и применение численного метода для нахождения решения

· Обработка результатов вычислений

· Сравнение с результатами натурного эксперимента

· Принятие решения о продолжении натурных экспериментов

· Продолжение натурного эксперимента для получения данных, необходимых для уточнения модели

· Накопление экспериментальных данных

· Построение математической модели

· Автоматическое построение программной реализации математической модели

· Автоматизированное нахождение численного решения

· Автоматизированное преобразования результатов вычислительных в форму, удобную для анализа

· Принятие решения о продолжении натурных экспериментов

Видоизмененная цепочка реализованная в виде единого программного комплекса и со­ставляет «технологию» вычислительного эксперимента.

В наиболее общем виде этапы вычислительного эксперимента можно представить в виде последовальности технологических операций (они реализованы в соответствующих блоках про­граммного комплекса):

Построение математической модели.

Преобразование математической модели.

Планирование вычислительного эксперимента.

Построение программной реализации математической модели

Отладка и тестирование программной реализации.

Проведение вычислительного эксперимента.

Для проведения крупномасштабных научных исследований используется модульная техно­логия, основанная на модульном представлении: математических моделей; вычислительных алго­ритмов; программ для ЭВМ; технических средств. Сборка программ из модулей проводится авто­матически, с помощью специальной программы. Создаются программные комплексы и проблем­но-ориентированные пакеты прикладных программ многоцелевого назначения. Характерная осо­бенность пакетов состоит в возможности постоянного развития, расширения благодаря включе­нию новых модулей, реализующих новые возможности. Следует отметить, что один и тот же па­кет прикладных программ может быть использован в вычислительных экспериментах для иссле­дований различных реальных объектов.

3. Сферы применения вычислительного эксперимента и математического моделирования

В современной науке и технике появляется всё больше областей, задачи в которых можно и нужно решать методом вычислительного эксперимента, с помощью математического модели­рования. Обратим внимание на некоторые из них.

Энергетическая проблема. Прогнозирование атомных и термоядерных реакторов на осно­ве детального математического моделирования происходящих в них физических процессов. В этой области работа ведётся очень успешно. Вычислительный эксперимент тесно сопрягается с натурным экспериментом и помогает, заменяет и удешевляет весь исследовательский цикл, суще­ственно его ускоряя.

Космическая техника. Расчёт траекторий летательных аппаратов, задачи обтекания, систе­мы автоматического проектирования. Обработка данных натурного эксперимента, например ра­диолокационных данных, изображений со спутников, диагностика плазмы. Здесь очень важной оказывается проблема повышения качества приборов, и в частности измерительной аппаратуры. Между тем, в настоящее время показано, что, используя измерительный прибор среднего качества и присоединив к нему ЭВМ, можно на основе специальных алгоритмов получить результаты, ко­торые дал бы измерительный прибор очень высокого качества. Таким образом, сочетание изме­рительного прибора с компьютером открывает новые возможности.

Технологические процессы. Получение кристаллов и плёнок, которые, кстати, нужны для создания вычислительной техники, для решения проблем в области элементарной базы ( что не­возможно без математического моделирования ); моделирование теплового режима конструктив­ных узлов перспективных ЭВМ, процессов лазерной плазмы, технологии создания материалов с заданными свойствами ( это одна из основных задач любой технологии ).

Экологические проблемы. Вопросы прогнозирования и управления экологическими систе­мами могут решаться лишь на основе математического моделирования, поскольку эти системы существуют в “единственном экземпляре”.

Гео- и астрофизические явления. Моделирование климата, долгосрочный прогноз погоды, землетрясений и цунами, моделирование развития звёзд и солнечной активности, фундаменталь­ные проблемы происхождения и развития Вселенной.

Химия. Расчёт химических реакций, определение их констант, исследование химических процессов на макро- и микроуровне для интенсификации химической технологии.

Биология. Особо следует отметить интерес к математическому моделированию в связи с изучением фундаментальных проблем этой науки ( генетики, морфогенеза ) и разработкой новых методов биотехнологии.

Анализ математических моделей с помощью вычислительного эксперимента с каждым го­дом завоёвывает новые позиции. В 1982 г. Нобелевская премия по физике была присуждена К. Вильсону, предложившему ряд фундаментальных моделей в теории элементарных частиц и кри­тических явлений, которые необходимо исследовать численно. В 1979 г. Нобелевской премией по медицине была удостоена работа в области вычислительной томографии (восстановление объём­ного предмета по набору его сечений). В 1982 г. Нобелевской премией по химии отмечена рабо­та, в которой методами вычислительной томографии восстанавливалась структура вируса по дан­ным электронной микроскопии.

Каждая из этих работ приводит к постановке глубоких математических задач, для решения которых необходим вычислительный эксперимент. При постановке вычислительного экспери­мента в различных областях используются пакеты прикладных программ.

4. Результаты расчёта последствий ядерного конфликта

Похолодание на планете приведёт к гибели многих видов животных и растений. У человечества будет ну много шансов приспособиться к новой экологической обстановке. Подчеркнём ещё раз, что такая модель была построена для сценариев ограниченной, “контролируемой” ядерной войны. Аналогичные результаты были получены позже учёными США и Великобритании. Они использовали другие математические модели и более мощные вычислительные средства.

5.Пакеты прикладных программ

Остановимся несколько подробнее на этом [3] важном направлении современного програм­мирования. Чтобы лучше ощутить существующие здесь проблемы и понять пути их решения, об­ратимся к истории вопроса, благо история эта ещё весьма коротка.

Если математическая модель претерпевала заметные изменения ( например, в уравнениях магнитной гидродинамики требовалось учесть не одну, а две компоненты вектора напряжённости магнитного поля или дополнительно учесть излучение ), то также естественно было не создавать новую программу, а “надстраивать” старую, уже хорошо зарекомендовавшую себя в расчётах.

Программа разрасталась, разветвлялась, её возможности повышались. С помощью такого комбайна можно было решать и прежние простые задачи. Чем сложнее становился программный комбайн, чем большими возможностями он обладал, тем обширнее становилась таблица ключе­вых параметров.

Постепенно программа превращалась в эдакого монстра, нашпигованного ключевыми па­раметрами. Новые “заплаты” ставились на старые, и в этих дебрях начинал путаться сам автор программы. В конце концов принималось решение переписать программу заново, а это означало, что придётся повторно тратить немалое время и силы на большую трудоёмкую работу.

Одним из средств борьбы с такими непроизводительными потерями являются пакеты при­кладных программ.

Пакет прикладных программ ( ППП ) состоит из функционального наполнения и систем­ной части. Функциональное наполнение представляет собой, грубо говоря, набор отдельных про­грамм, решающих конкретные задачи. Эти задачи объединены одной направленностью, или, как говорят, предметной областью. Дело в том, что ППП не является универсальным, он проблемно-ориентирован, т.е. предназначен для решения определённого класса задач.

Если это задачи механики сплошной среды, то в функциональное наполнение могут вхо­дить, например, программы для расчёта уравнений газовой динамики, уравнения теплопроводно­сти, уравнений для электромагнитного поля, уравнений для излучения, фазовых переходов и т.д.

Содержание каждой такой индивидуальной программы, или “модуля”, специфично, однако требования к оформлению входной и выходной информации унифицированы. Эти модули пред­ставляют собой своеобразные “чёрные ящики”, которые можно соединять в цепочки, ветви, так, чтобы в конце концов получить заданную программу.

Системная часть выполняет функции сервисного характера. Основные задачи здесь состоят в следующем. Прежде всего необходимо организовать хранение функционального наполнения. Но хранить в данном случае не значит ограничиться записью информации на каких-либо носите­лях. В этом архиве должен быть порядок: по первому требованию указанный модуль должен быть направлен “в работу”.

Конечно же это очень упрощённая схема работы с пакетом, но она отражает характерные этапы такой деятельности.

Кроме того, для того чтобы пользоваться пакетом и, значит, грамотно вести расчёты, сов­сем не обязательно самому обладать высокой квалификацией программиста или математика-вы­числителя ( ведь именно они должны создавать эти пакеты ). Поэтому пакеты программ должны быть такими, чтобы к их помощи могли прибегнуть не только математики, но и специалисты дру­гих сфер научной деятельности, прошедшие сравнительно небольшой курс математического обу­чения.

Источник