что такое выброс в статистике
Что такое выброс в статистике
В рамках проектной деятельности, которую осуществляют участники тренинга шести сигм для зеленых поясов, часто приходится сталкиваться с нетривиальными задачами, решение которых не столь очевидно, а порой требует творческого подхода. Одной из таких задач является работа с выбросами перед расчетом описательных статистик и способности процесса на этапе измерений (Measure). В этой и ряде последующих публикаций попробуем разобраться в том, что такое выбросы и почему так важно знать о них, как они возникают и что с ними делать?
Итак, что же такое выбросы?
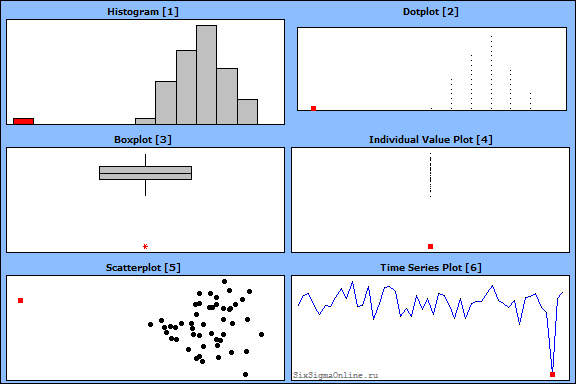
Выброс – это результат измерения, выделяющийся из общей выборки. Иными словами, выбросы – это необычно низкие или высокие значения наблюдаемой величины, причем настолько, что это заметно невооруженным глазом: в ходе графического анализа наблюдений вы можете заметить значения, которое не принадлежит популяции наблюдений. Определить выбросы можно с помощью: гистограмм [1], точечных [2] и ящичных [3] диаграмм, диаграмм индивидуальных значений [4], рассеяния [5] и даже диаграмм временных рядов [6]:
красные точки, звездочки и столбцы на диаграммах соответствуют выбросам
В теории статистического анализа нет однозначного критерия идентификации выбросов, и это – первая причина, по которой выбросы представляют опасность для неопытного исследователя.
Из определения следует, что все необычно низкие или высокие значения наблюдаемой величины могут быть выбросами. Как же определить, какое значение переменной является необычно высоким или низким. Один из самых простых способов: использовать диапазон трех стандартных отклонений вокруг среднего значения. Вероятность выхода величины за пределы ±3σ составляет 0,0027, а значит, с большой долей вероятности, значение, которое выходит за пределы ±3σ не принадлежит к популяции.
С другой стороны, можно привести ряд доводов против этого утверждения. Например, оно теряет смысл, если функция распределения отличается от нормальной или размер выборки слишком мал, чтобы представить генеральную совокупность значений. Кроме того, с вероятностью 0,0027 наблюдение все же может выйти за пределы диапазона трех стандартных отклонений.
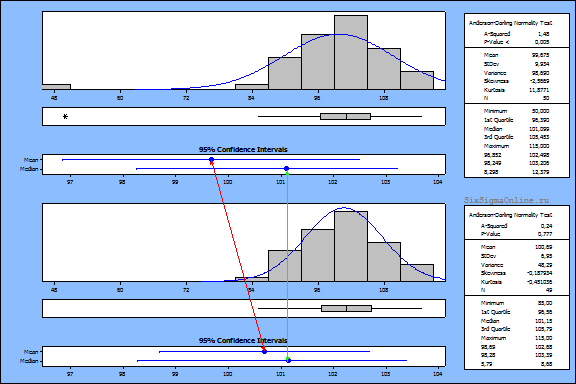
Вторая опасность, которую представляют выбросы – искажение статистик или результатов статистических расчетов. Такие показатели как среднее арифметическое (Mean), стандартное отклонение (StDev), асимметрия (Skewness), эксцесс (Kurtosis), а также критерий согласия с нормальным законом весьма подвержены влиянию выбросов. В отличие от среднего арифметического, медиана менее подвержена влиянию выбросов. На следующем рисунке медиана и среднее арифметическое до и после исключения выброса обозначены зеленой и красной стрелками соответственно:
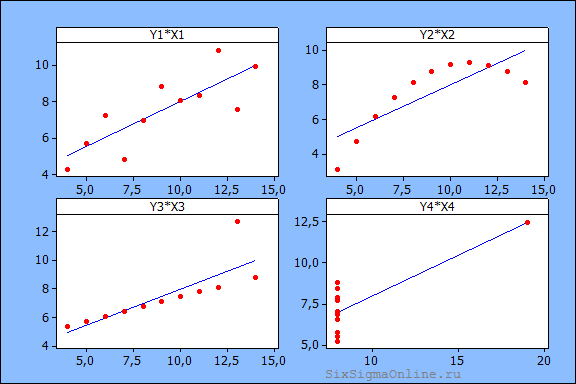
Еще один классический пример – квартет Энскомба (Anscomb):
| X1 | Y1 | X2 | Y2 | X3 | Y3 | X4 | Y4 |
| 10 | 8,04 | 10 | 9,14 | 10 | 7,46 | 8 | 6,58 |
| 8 | 6,95 | 8 | 8,14 | 8 | 6,77 | 8 | 5,76 |
| 13 | 7,58 | 13 | 8,74 | 13 | 12,74 | 8 | 7,71 |
| 9 | 8,81 | 9 | 8,77 | 9 | 7,11 | 8 | 8,84 |
| 11 | 8,33 | 11 | 9,26 | 11 | 7,81 | 8 | 8,47 |
| 14 | 9,96 | 14 | 8,1 | 14 | 8,84 | 8 | 7,04 |
| 6 | 7,24 | 6 | 6,13 | 6 | 6,08 | 8 | 5,25 |
| 4 | 4,26 | 4 | 3,1 | 4 | 5,39 | 19 | 12,5 |
| 12 | 10,84 | 12 | 9,13 | 12 | 8,15 | 8 | 5,56 |
| 7 | 4,82 | 7 | 7,26 | 7 | 6,42 | 8 | 7,91 |
| 5 | 5,68 | 5 | 4,74 | 5 | 5,73 | 8 | 6,89 |
Квартет Энскомба – это четыре набора числовых данных, которые используют как свидетельство важности визуальной оценки наблюдений в корреляционном и регрессионном анализе:
Не смотря на различия взаимосвязи переменных X и Y, во всех четырех случаях статистические показатели, как и уравнение линейной регрессии, одинаковы:
| Характеристика | Значение |
| Среднее значение переменной X | 9.0 |
| Дисперсия переменной X | 10 |
| Среднее значение переменной Y | 7,5 |
| Дисперсия переменной Y | 3,75 |
| Коэффициент корреляции Пирсона | 0,816 |
| Уравнение линейной регрессии | Y=3+0.5X |
Обратите внимание на третий и четвертый наборы данных. Выброс в третьем примере искажает уравнение зависимости, а в четвертом – заставляет принять решение о наличии корреляции, в то время как ее на самом деле нет.
И, наконец, третья опасность, которую таят выбросы – это легкость их неверного истолкования, что, в свою очередь, приведет к неверному направлению последующего анализа. Наличие выбросов может означать ошибку ввода данных, недостаточную величину выборки или присутствие специальной причины отклонения – действие конкретного фактора или причины. Диагностируя выбросы, легко допустить ошибку, исключив нужные для анализа данные или наоборот – рассчитав показатели процесса, используя неверные результаты наблюдений.
Таким образом, существует, по меньшей мере, 3 причины, почему выбросы данных следует исследовать. Невнимательное отношение к выбросам наблюдений ставит под угрозу выводы о наблюдении процесса и ставит под угрозу результаты последующего анализа. Следовательно, обнаружив необычно низкие или высокие значения наблюдаемой величины, исследователь обязан найти причину их появления, прежде чем делать выводы о наблюдаемой переменной или приступать к последующему анализу данных. Наиболее вероятные причины появления выбросов будут рассмотрены в следующей статье.
Как использовать статистику для выявления выбросов в данных
Дата публикации 2018-04-25
При моделировании важно очистить выборку данных, чтобы убедиться, что наблюдения наилучшим образом представляют проблему.
Иногда набор данных может содержать экстремальные значения, которые выходят за пределы ожидаемого и отличаются от других данных. Они называются выбросами, и часто модели машинного обучения и навыки моделирования в целом могут быть улучшены путем понимания и даже устранения этих значений выбросов.
В этом руководстве вы узнаете больше о выбросах и двух статистических методах, которые можно использовать для идентификации и фильтрации выбросов из набора данных.
После завершения этого урока вы узнаете:
Обзор учебника
Этот урок разделен на 4 части; они есть:
Что такое выбросы?
Это редко, или отчетливо, или не подходит в некотором роде.
Выбросы могут иметь много причин, таких как:
Не существует точного способа определения и идентификации выбросов в целом из-за специфики каждого набора данных. Вместо этого вы или эксперт в области должны интерпретировать необработанные наблюдения и решить, является ли значение выбросом или нет.
Тем не менее, мы можем использовать статистические методы для выявления наблюдений, которые кажутся редкими или маловероятными с учетом имеющихся данных.
Это не означает, что указанные значения являются выбросами и должны быть удалены. Но инструменты, описанные в этом руководстве, могут помочь пролить свет на редкие события, которые могут потребовать второго взгляда.
Тестовый набор данных
Прежде чем мы рассмотрим методы идентификации выбросов, давайте определим набор данных, который мы можем использовать для тестирования методов.
Мы сгенерируем 10 000 случайных чисел из гауссовского распределения со средним значением 50 и стандартным отклонением 5.
Числа, взятые из гауссовского распределения, будут иметь выбросы. То есть в силу самого распределения будет несколько значений, которые будут далеки от средних, редких значений, которые мы можем определить как выбросы.
Мы будем использоватьrandn ()функция для генерации случайных гауссовских значений со средним значением 0 и стандартным отклонением 1, затем умножьте результаты на наше собственное стандартное отклонение и добавьте среднее значение для смещения значений в предпочтительный диапазон.
Генератор псевдослучайных чисел засеян, чтобы гарантировать, что мы получаем одну и ту же выборку чисел при каждом запуске кода.
При выполнении примера генерируется образец, а затем выводится среднее значение и стандартное отклонение. Как и ожидалось, значения очень близки к ожидаемым.
Метод стандартных отклонений
Если мы знаем, что распределение значений в выборке является гауссовским или гауссовидным, мы можем использовать стандартное отклонение выборки в качестве предела для выявления выбросов.
Гауссово распределение обладает свойством того, что стандартное отклонение от среднего может использоваться для надежного суммирования процентного значения в выборке.
Например, в пределах одного стандартного отклонения среднее будет охватывать 68% данных.
Таким образом, если среднее значение равно 50, а стандартное отклонение равно 5, как в тестовом наборе данных выше, то все данные в выборке между 45 и 55 будут составлять около 68% выборки данных. Мы можем охватить большую часть выборки данных, если расширим диапазон следующим образом:
Значение, которое выходит за пределы 3 стандартных отклонений, является частью распределения, но это маловероятное или редкое событие приблизительно в 1 из 370 выборок.
Давайте сделаем это на конкретном примере.
Иногда данные сначала стандартизируются (например, до Z-показателя с нулевым средним и единичной дисперсией), чтобы обнаружение выброса можно было выполнить с использованием стандартных значений отсечения Z-показателя. Это удобно и не требуется вообще, и мы сделаем вычисления в исходном масштабе данных здесь, чтобы прояснить ситуацию.
Мы можем рассчитать среднее и стандартное отклонение для данной выборки, а затем рассчитать порог для определения выбросов как более 3 стандартных отклонений от среднего.
Затем мы можем определить выбросы как те примеры, которые выходят за пределы определенных нижних и верхних пределов.
Кроме того, мы можем отфильтровать те значения из выборки, которые не находятся в определенных пределах.
Мы можем собрать все это вместе с нашим образцом набора данных, подготовленным в предыдущем разделе.
Полный пример приведен ниже.
Выполнение примера сначала выведет количество идентифицированных выбросов, а затем число наблюдений, которые не являются выбросами, демонстрируя, как идентифицировать и отфильтровать выбросы соответственно.
До сих пор мы говорили только об одномерных данных с гауссовым распределением, например одна переменная. Вы можете использовать тот же подход, если у вас есть многомерные данные, например, данные с несколькими переменными, каждая с разным распределением Гаусса.
Вы можете представить границы в двух измерениях, которые бы определяли эллипс, если у вас есть две переменные. Наблюдения, которые выходят за пределы эллипса, будут считаться выбросами. В трех измерениях это будет эллипсоид и т. Д. В более высокие измерения.
С другой стороны, если вы знали больше о домене, возможно, можно определить выброс, превышая пределы одного или подмножества измерений данных.
Межквартильный метод
Не все данные являются нормальными или достаточно нормальными, чтобы рассматривать их как взятые из гауссовского распределения.
Хорошей статистикой для суммирования выборки негауссовых распределений данных является Interquartile Range, или IQR для краткости.
IQR рассчитывается как разница между 75-м и 25-м процентилями данных и определяет прямоугольник на графике прямоугольника и вискера.
Мы называем процентили квартилями («кварта4) потому что данные делятся на четыре группы через 25-е, 50-е и 75-е значения.
IQR определяет средние 50% данных, или тело данных.
IQR может использоваться для определения выбросов путем определения пределов значений выборки, которые являются факторомКIQR ниже 25-го процентиля или выше 75-го процентиля. Общее значение для фактораКэто значение 1,5. Коэффициент k, равный 3 или более, можно использовать для определения значений, которые являются экстремальными выбросами или «дальние выходы”, Когда описано в контексте рамок и усов.
На графике бокса и усов эти пределы изображены в виде заборов на усиках (или линиях), которые нарисованы из бокса. Значения, которые выходят за пределы этих значений, отображаются в виде точек.
Мы можем рассчитать процентили набора данных, используяпроцентиля ()Функция NumPy, которая принимает набор данных и спецификацию желаемого процентиля. Затем IQR можно рассчитать как разницу между 75-м и 25-м процентилями.
Затем мы можем рассчитать пороговое значение для выбросов как 1,5-кратное IQR и вычесть это пороговое значение из 25-го процентиля и добавить его к 75-му процентилю, чтобы получить фактические пределы данных.
Затем мы можем использовать эти пределы для определения значений выбросов.
Мы также можем использовать пределы, чтобы отфильтровать выбросы из набора данных.
Мы можем связать все это вместе и продемонстрировать процедуру на тестовом наборе данных.
Полный пример приведен ниже.
При выполнении примера сначала выводятся идентифицированные 25-й и 75-й процентили и вычисленный IQR. Печатается число выявленных выбросов, а затем число наблюдений, не связанных с выбросами.
Подход может быть использован для многомерных данных путем расчета пределов для каждой переменной в наборе данных по очереди и с учетом выбросов в качестве наблюдений, которые выходят за пределы прямоугольника или гипер-прямоугольника.
расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
Если вы исследуете какое-либо из этих расширений, я хотел бы знать.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться
Сообщений
статьи
Резюме
В этом руководстве вы обнаружили выбросы и два статистических метода, которые можно использовать для идентификации и фильтрации выбросов из набора данных.
В частности, вы узнали:
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Что такое выброс в статистике
ГОСТ Р ИСО 16269-4-2017
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Выявление и обработка выбросов
Statistical methods. Statistical data presentation. Part 4. Detection and treatment of outliers
Дата введения 2018-12-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (АО «НИЦ КД») на основе собственного перевода на русский язык англоязычной версии международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Применение статистических методов»
Международный стандарт разработан Техническим комитетом ISO/ТС 69.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА*
Введение
Выбросы могут искажать и сокращать информацию, содержащуюся в источнике данных или процедуре их генерации. В производстве наличие выбросов снижает результативность производственных процессов, качество продукции, а также процедур контроля продукции. Выбросы не всегда следует трактовать как «плохие» или «ошибочные» данные. В некоторых случаях выбросы дают важную информацию, которую необходимо учитывать в процессе исследований.
Выявление и анализ выбросов в процессе измерения ведут к более полному пониманию изучаемых процессов и более глубокому анализу данных, и как следствие, к более достоверным выводам.
Так как проблеме обнаружения и обработки выбросов посвящено большое количество литературных публикаций, важной задачей является определение и стандартизация (на международном уровне) этих методов.
Настоящий стандарт содержит шесть приложений. В приложении A приведен алгоритм вычисления статистик и критических значений для выявления выбросов в выборке из нормального распределения. В приложениях B, D и E приведены таблицы, необходимые для применения рекомендованных в стандарте процедур. В приложении C приведено статистическое обоснование построения диаграмм, помогающих в решении задачи отслеживания выбросов. В приложении F приведено поэтапное руководство по применению процедур, установленных в настоящем стандарте, и представлена блок-схема соответствующих действий.
1 Область применения
В настоящем стандарте установлены статистические критерии и методы графического анализа данных, полученные в результате измерений. В настоящем стандарте приведены рекомендации по методам определения робастных оценок и процедурам проверки наличия выбросов в данных.
Методы, представленные в настоящем стандарте, предназначены главным образом для выявления и обработки выбросов одномерных данных. Однако в настоящем стандарте представлены также некоторые рекомендации по работе с многомерными данными и данными регрессионного анализа.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 выборка, набор данных (sample, data set): Подмножество генеральной совокупности, состоящее из одной или нескольких выборочных единиц.
2.2 выброс (outlier): Элемент маломощного подмножества выборки, существенно отличающийся от остальных элементов выборки (2.1).
2.3 маскировка (masking): Наличие более одного выброса (2.2), затрудняющее обнаружение каждого выброса.
2.4 вероятность ложного обнаружения выбросов (some-outside rate): Вероятность того, что одно или несколько наблюдений незагрязненной выборки, ошибочно классифицированы как выбросы (2.2).
2.5 метод коррекции выбросов (outlier accommodation method): Метод нечувствительный к наличию выбросов (2.2) при принятии решения о генеральной совокупности.
2.6 устойчивая оценка (resistant estimation): Оценка, подверженная лишь малым изменениям при замене небольшой доли набора данных (2.1), элементами, возможно, имеющими значительное отличие от замененных элементов.
2.7 робастная оценка (robust estimation): Оценка, нечувствительная к небольшим отклонениям от предполагаемой вероятностной модели данных.
2.8 ранг (rank): Положение наблюдаемого значения в упорядоченном наборе наблюдаемых значений.
2.9 глубина (depth): Наименьший из двух рангов (2.8), присвоенных элементу при упорядочивании выборки (2.1) в неубывающем и невозрастающем порядках.
2.10 порядковая статистика (order statistic): Статистика, определяемая рангом при упорядочивании набора данных в неубывающем порядке.
[ИСО 3534-1:2006, п.1.13]
2.12 первый квартиль, нижний выборочный квартиль (first quartile, sample lower quartile, ): Медиана (2.11) первых наименьших (n-1)/2 значений для нечетного числа наблюдений; медиана первых наименьших n/2 значений для четного числа наблюдений.
2.13 третий квартиль, верхний выборочный квартиль (third quartile, sample upper quartile, ): Медиана (2.11) последних наибольших (n-1)/2 значений для нечетного числа наблюдений или медиана последних наибольших n/2 значений для четного числа наблюдений.
2.14 межквартильный размах IQR (interquartile range, IQR): Разность третьего квартиля (2.13) и первого квартиля (2.12).
2.15 сводка пяти чисел (five-number summary): Набор значений выборочного минимума, первого квартиля (2.12), медианы (2.11), третьего квартиля (2.13) и выборочного максимума.
2.16 диаграмма ящик с усами (box plot): Графическое представление (горизонтальное или вертикальное) сводки пяти чисел (2.15).
Выброс (статистика)
Статистический метод, способный действовать в условиях выбросов, называется робастным. Медиана является робастной характеристикой, а выборочное среднее — нет. Существует пример (квартет Энскомба), демонстрирующий, насколько неробастные методы обработки статистических данных способны «врать», даже если выброс всего один на 10 «обычных» результатов.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.
Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых.
Техники спектральной кластеризации используют спектр (собственные значения) матрицы сходства данных для осуществления понижения размерности перед кластеризацией в пространствах меньших размерностей. Матрица сходства подаётся в качестве входа и состоит из количественных оценок относительной схожести каждой пары точек в данных.
Блог об аналитике, визуализации данных, data science и BI
Дашборд первых 8 месяцев жизни малыша
Анализ рынка вакансий аналитики и BI: дашборд в Tableau
Анализ альбомов Земфиры: дашборд в Tableau
Гайд по современным BI-системам
Обнаружение статистических выбросов в R
Этот материал — перевод статьи «Outliers detection in R». А ещё у нас есть материал про обнаружение выбросов в Python.
Выбросы — значения или наблюдения, отклоняющиеся от других данных. Всегда нужно сравнивать наблюдение с другими значениями, полученными тем же способом, прежде чем называть их выбросами. Действительно, человек с ростом 200 см, скорее всего, будет считаться отклонением по сравнению с остальным населением, но этот же человек не будет считаться статистическим выбросом, если мы измерим рост баскетболистов.
Выбросы могут быть вызваны изменчивостью, присущей наблюдаемому явлению. Например, при сборе данных о заработной плате часто возникают выбросы, поскольку некоторые люди зарабатывают гораздо больше остальных. Выбросы также могут возникать из-за экспериментальной ошибки, ошибки измерения или кодирования. Например, вес человека 786 кг явно является ошибкой при кодировании веса объекта. Её или его вес, скорее всего, составляет 78,6 кг или 7,86 кг в зависимости от того, был измерен вес взрослого человека или ребёнка.
По этой причине иногда имеет смысл формально выделять два класса выбросов: экстремальные значения и ошибки. Экстремальные значения интереснее, потому что они возможны, но маловероятны.
В этой статье я представлю несколько подходов к обнаружению выбросов в R от простых методов, таких как описательная статистика (включая минимальные, максимальные значения, гистограмму, прямоугольную диаграмму и процентили), до более формальных методов, таких как фильтр Хэмпеля, тесты Граббса, Диксона и Рознера.
Не существует строгого и однозначного правила насчет того, следует ли удалять выбросы из набора данных перед проведением статистического анализа. Довольно часто переменные значения, вызванные экспериментальной ошибкой или ошибкой измерения удаляются или заменяются на новые значения. Некоторые статистические тесты требуют их отсутствия, чтобы сделать обоснованные выводы, но удаление выбросов рекомендуется не во всех случаях и должно выполняться с осторожностью.
Эта статья поможет обнаружить и проверить выбросы, но вы не узнаете, следует ли удалять, изменять или оставлять такие значения. После проверки вы можете исключить их или включить в свой анализ (а это обычно требует вдумчивого размышления со стороны исследователя). Удаление или сохранение выбросов, в основном, зависит от трех факторов:
Мы будем использовать набор данных mpg из библиотеки ggplot2, чтобы проиллюстрировать различные подходы к обнаружению выбросов в R, и в частности, мы сосредоточимся на работе с переменной hwy (пробег в милях на галлон израсходованного топлива).
Минимальные и максимальные значения
Первое, что необходимо для обнаружения выбросов в R — начать с описательной статистики, и, в частности, с минимальных и максимальных значений.
В R это легко сделать с помощью функции summary():
Минимум и максимум — первое и последнее значения в выходных данных выше. В качестве альтернативы, их также можно вычислить с помощью функций min() и max():
Явная ошибка кодирования, такая как, например, человеческий вес в 786 кг уже будет легко обнаружена с помощью этой простой техники.
Другой базовый способ обнаружения выбросов — построение гистограммы данных.