что такое вспомогательный угол

10.12.202317.04.2022 admin 0 Comments

Метод введения вспомогательного угла

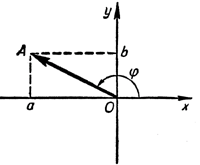
Преобразование выражения a sin х + b cos х путем введения вспомогательного угла

Другими словами, если а 2 + b 2 = 1, то существует угол φ, такой, что

Прежде чем доказывать эту лемму, поясним ее на следующем примере:

Поэтому существует угол φ, такой, что $ \frac<\sqrt3> <2>$ = cos φ; 1 /₂ = sin φ.

В качестве φ в данном случае можно выбрать любой из углов 30°, 30° ± 360°, 30° ± 2 • 360° и т. д.

Итак, а = cos φ; b =sin φ, что и требовалось доказать.

Доказанная лемма позволяет преобразовать выражение a sin х + b cos х к более удобному для изучения виду.

Прежде всего вынесем за скобки выражение $\sqrt$

a sin х + b cos х = $\sqrt$(cos φ sin х + sin φ cos х) = $\sqrt$ sin ( x + φ )

1) $ sin x + cos x = \sqrt2 (\frac<1> <\sqrt2>sin x + \frac<1><\sqrt2>cos x) = \sqrt2 (cos\frac<\pi><4>sin x + sin\frac<\pi><4>cos x ) =\\= \sqrt2(sinx + \frac<\pi><4>) $

Полученную формулу sin x + cos x = $\sqrt2(sinx + \frac<\pi><4>)$полезно запомнить.

2) Если одно из чисел а и b положительно, а другое отрицательно, то выражение
a sin х + b cos х удобнее преобразовывать не к синусу суммы, а к синусу разности двух углов. Так,

где под φ можно подразумевать любой угол, удовлетворяющий условиям:

В частности, можно положить φ = arctg 4 /₃. Тогда получим:

Источник

Метод вспомогательного угла в тригонометрических уравнениях

На уроках алгебры учителя рассказывают, что существует небольшой (на самом деле — очень даже большой) класс тригонометрических уравнений, которые не решаются стандартными способами — ни через разложение на множители, ни через замену переменной, ни даже через однородные слагаемые. В этом случае в дело вступает принципиально другой подход — метод вспомогательного угла.

Что это за метод и как его применять? Для начала вспомним формулы синуса суммы/разности и косинуса суммы/разности:

\[\begin& \sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\& \cos \left( \alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\\end\]

Думаю, эти формулы хорошо знакомы вам — из них выводятся формулы двойного аргумента, без которых в тригонометрии вообще никуда. Но давайте теперь рассмотрим простое уравнение:

Разделим обе части на 5:

\[\begin& \cos \alpha \sin x+\sin \alpha \cos x=1 \\& \sin \left( \alpha +x \right)=1 \\\end\]

Сегодня мы будем разбирать решение тригонометрических уравнений, а, точнее, один-единственный прием, который называется «метод вспомогательного угла». Почему именно этот метод? Просто потому, что за последние два-три дня, когда я занимался с учениками, которым рассказывал о решении тригонометрических уравнений, и мы разбирали, в том числе, метод вспомогательного угла, и все ученики как один допускают одну и ту же ошибку. А ведь метод вообщем-то несложный и, более того, это один из основных приемов в тригонометрии. Поэтому многие тригонометрические задачи иначе как методом вспомогательного угла вообще не решаются.

Поэтому сейчас для начала мы рассмотрим пару простеньких задач, а потом перейдем к задачам посерьезней. Однако все эти они так или иначе потребуют от нас применение метода вспомогательного угла, суть которого я расскажу уже в первой конструкции.

Решение простых тригонометрических задач

Пример № 1

Немного преобразуем наше выражение:

\[\sqrt<3>\cdot \sin 2x-\cos 2x=1\]

\[\sin \left( \alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \]

Вернемся к нашему примеру. Все сведем к синусу разности. Но для начала уравнение необходимо немного преобразовать. Найдем коэффициент:

$\sqrt$ — это тот самый коэффициент, на который необходимо разделить обе части уравнения, чтобы перед синусом и косинусом появились числа, которые сами по себе являются синусами и косинусами. Давайте разделим:

Теперь перед нами формула синуса разности. Мы можем написать так:

Перед нами простейшая классическая тригонометрическая конструкция. Напомню:

Это и запишем для нашего конкретного выражения:

Нюансы решения

Итак, что нужно делать, если вам попалось подобный пример:

В связи с этим у внимательных учеников наверняка возникнет два вопроса.

Метод вспомогательного угла — это инструмент, который помогает свести «некрасивое» уравнение к вполне адекватному и «красивому».

Пример № 2

Нам потребуется только первые выкладки. Давайте приступим к работе над задачей:

\[\sqrt<3>\cdot \sin 2x+2\cdot \frac<1-\cos 2x><2>-1=2\cos x\]

\[\sqrt<3>\cdot \sin 2x+1-\cos 2x-1=2\cos x\]

\[\sqrt<3>\cdot \sin 2x-\cos 2x=2\cos x\]

Перепишем с учетом этого факта:

\[\frac<\sqrt<3>><2>\cdot \sin 2x-\frac<1><2>\cdot \cos 2x=\cos x\]

Внесем «минус» в скобку хитрым способом. Для этого заметим следующее:

Чтобы решить подобною задачу, нужно вспомнить такое:

\[\cos \alpha =\cos \beta \]

\[\left[ \begin& \alpha =\beta +2\text< >\!\!\pi\!\!\text< >n \\& \alpha =-\beta +2\text< >\!\!\pi\!\!\text< >n \\\end \right.\]

Разберемся с нашим примером:

Давайте посчитаем каждое из этих уравнений:

Запишем окончательный ответ:

Нюансы решения

На самом деле, это выражение решается множеством различных способов, однако именно метод вспомогательного угла является в данном случае оптимальным. Кроме того, на примере данной конструкции хотелось бы обратить ваше внимание еще на несколько интересных приемов и фактов:

Разбор более сложных задач

Пример № 1

Преобразуем первое слагаемое:

\[\sin 3x=\sin \left( 2x+x \right)=\sin 2x\cdot \cos x+\cos 2x\cdot \sin x\]

\[=2\left( 1-\cos 2x \right)\cdot \sin x\]

А теперь подставим все это в нашу исходную конструкцию:

\[\sin 2x\cos x+\cos 2x\sin x+2\sin x-2\cos x\sin x+4\cos x=5\]

\[\sin 2x\cos x-\operatorname-cos2\sin x+2\sin x+4\cos x=5\]

\[\sin \left( 2x-x \right)+2\sin x+4\cos x=5\]

Давайте введем нашу поправку:

\[\sin x\cdot \cos \varphi +\cos x\cdot \sin \varphi =1\]

\[\sin \left( x+\varphi \right)=1\]

Это частный случай, простейшая тригонометрическая конструкция:

Начертим радар и посмотрим, где такие значения встречаются:

Возвращаясь к нашему выражению, мы напишем следующее:

Но и эту запись можно немного оптимизировать. Поскольку мы знаем следующее:

то в нашем случае можно записать так:

Пример № 2

Здесь потребуется еще более глубокое понимание методик решения стандартных задач без тригонометрии. Но для решения этого примера мы также используем метод вспомогательного угла.\[\]

\[5+2\sin 2x-5\cos x=5\sin x\]

Первое, что бросается в глаза — здесь нет степеней выше первой и поэтому ничего нельзя разложить по формулам разложения степеней. Воспользуется обратными выкладками:

\[5+4\sin x\cos x-5\cos x-5\sin x=0\]

\[3+2+4\sin x\cos x-5\left( \sin x+\cos x \right)=0\]

\[3+2\left( 1+2\sin x\cos x \right)-5\left( \sin x\cos x \right)=0\]

\[3+2\left( <<\sin >^<2>>x+2\sin x\cos x+co<~~^<2>>x \right)-5\left( \sin x+\cos x \right)=0\]~~

~~Что дает нам такая запись? Дело в том, что в первой скобке стоит точный квадрат. Свернем его и получим:~~

~~Предлагаю ввести новую переменную:~~

~~В этом случае мы получим выражение:~~

~~\[\left[ \begin& \sin x+\cos x=\frac<3> <2>\\& \sin x+\cos x=1 \\\end \right.\]~~

~~Разбираемся с каждым из этих выражений.~~

Первое уравнение корней не имеет, и для доказательства этого факта нам поможет иррациональность в знаменателе. Заметим следующее:

~~Разбираемся со вторым:~~

~~Решаем эту конструкцию:~~

~~В принципе, можно оставить ответ таким, а можно его расписать:~~

Важные моменты

Такая проблема возникает только тогда, когда речь идет о «некрасивых» аргументах. Когда у нас табличные значения, то ничего такого нет.

Надеюсь, сегодняшний урок помог вам разобраться, что такое метод вспомогательного угла и как его применять на примерах разного уровня сложности. Но это не единственный урок, посвященный решению задач методом вспомогательного угла. Поэтому оставайтесь с нами!

~~Источник~~

Решение тригонометрических неоднородных линейных уравнений (страница 2)

$\blacktriangleright$ Формула вспомогательного аргумента: \[\begin <|c|>\hline \text<Общий случай>\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin<(\alpha\pm \phi)>, \ \ \cos\phi=\dfrac a<\sqrt>, \ \sin\phi=\dfrac b<\sqrt>\\\\ \hline \text<Частный случай>\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin<\left(\alpha\pm \dfrac<\pi>4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>3\right)>\\\\ \hline \end\]

Таким образом, по данной формуле уравнение сводится к уравнению \[\large<\sqrt\cdot \sin<(x+ \phi)>=c \Longleftrightarrow \sin <(x+\phi)>=\dfrac c<\sqrt>>\] Учитывая область допустимых значений синуса, данное уравнение будет иметь корни только в том случае, если
\[-1\leq \dfrac c<\sqrt>\leq 1\]

~~а) Решите уравнение \[\sin 2x\sin \dfrac<2\pi>5+\cos2\left(\dfrac<\pi>2-x\right)\cos \dfrac<3\pi>5=1\]~~

~~а) Заметим, что по формулам приведения:~~

~~Следовательно, уравнение переписывается в виде~~

~~\[\sin 2x\sin\dfrac<2\pi>5+\cos2x\cos\dfrac<2\pi>5=1 \quad \Rightarrow \quad \cos\left(2x-\dfrac<2\pi>5\right)=1 \quad \Rightarrow\]~~

~~(преобразование было сделано по формуле косинуса разности $\cos\alpha\cos\beta+\sin\alpha\sin\beta=\cos(\alpha-\beta)$ )~~

~~\[\Rightarrow \quad 2x-\dfrac<2\pi>5=2\pi n, n\in\mathbb \quad \Rightarrow \quad x=\dfrac<\pi>5+\pi n, n\in\mathbb\]~~

~~Источник~~