что такое волновой пакет

Волновой пакет

Полезное

Смотреть что такое «Волновой пакет» в других словарях:

ВОЛНОВОЙ ПАКЕТ — занимающее ограниченный объем и перемещающееся в пространстве волновое поле. Волновой пакет может быть разложен на сумму монохроматических волн, частоты которых лежат в определенном интервале; чем уже волновой пакет, тем больше этот интервал. При … Большой Энциклопедический словарь

ВОЛНОВОЙ ПАКЕТ — распространяющееся волн. поле, занимающее в каждый момент времени огранич. область пр ва. Возникновение В. п. возможно у волн любой природы (звуковых, эл. магн. и т. п.). Такой волн. «всплеск» в нек рой области пр ва может быть разложен на сумму… … Физическая энциклопедия

волновой пакет — цуг волн Последовательность непрерывных упругих волн, исходящих из одного источника и распространяющихся в одном направлении. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное… … Справочник технического переводчика

Волновой пакет — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия

волновой пакет — занимающее ограниченный объём и перемещающееся в пространстве волновое поле. Волновой пакет может быть разложен на сумму монохроматических волн, частоты которых лежат в определенном интервале; чем уже волновой пакет, тем больше этот интервал. При … Энциклопедический словарь

волновой пакет — bangų paketas statusas T sritis radioelektronika atitikmenys: angl. wave packet vok. Wellengruppe, f; Wellenpaket, n rus. волновой пакет, m pranc. groupe d ondes, m … Radioelektronikos terminų žodynas

волновой пакет — banginis paketas statusas T sritis fizika atitikmenys: angl. wave packet vok. Wellengruppe, f; Wellenpaket, n rus. волновой пакет, m pranc. paquet d’ondes, m … Fizikos terminų žodynas

волновой пакет акустической эмиссии — Механический сигнал, порождаемый единичным актом акустической эмиссии. [ГОСТ 27655 88] Тематики акустические измерения … Справочник технического переводчика

Источник

Начала физики. 32. Волновые пакеты. Неопределенности и принцип Гайзенберга на пальцах.

1. Корпускулярно-волновой антропоцентризм.
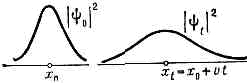
Наши мозги и язык всегда в той или иной степени идеализирует реальность. Когда мы говорим о волнах, то представляем себе, как правило, бесконечно длинную волну постоянной амплитуды с одинаковыми расстояниями между горбами волны. Но реальность не такова. Волны всегда образуют волновые пакеты (цуги волн). Примерно такие:

С большим или меньшим числом волновых горбов внутри пакета.

Кто и как будет воспринимать такой волновой пакет? В начале прошлого века связь и вещание велись на длинных (километры) и средних (сотни метров) электромагнитных волнах. И мы их назвали радиоволнами. Терминология не изменилась при переходе на короткие (десятки метров), ультракороткие (метры) и дециметровые (сотовая связь) волны. Но уже при переходе на диапазон длин волн от миллиметра до микрометра мы уже говорим об инфракрасном излучении, но не о волнах. А для обозначения более коротковолных диапазонов (начиная от видимого света на длинах волн

400-700 нанометров) пользуемся терминами фотоны и кванты. Подразумевая, тем самым, что пакеты таких волн мы воспринимаем как частицы.

Итак, понятие корпускулярно-волнового дуализма в немалой степени антропоцентрично. Поэтому вас не должен удивлять тот факт, что физики при описании многих коллективно-волновых явлений в сплошных стредах стали вводить понятия квазичастиц. Таких, как фононы, являющиеся по сути волновыми пакетами (квантами) колебаний кристаллических решеток в твердых телах.

2. Неопределенности и принцип Гайзенберга.
Тот факт, что волновой пакет имеет конечную длину Δ х, означает, что в таком пакете есть приличная примесь волн, длина которых отличается от основной, и которые в конечном счете гасят колебания ξ(x,t) на краях пакета. Это можно описать как наличие в пакете заметной примеси длин волн в диапазоне Δ λ в окрестности основной длины волны. Или примеси волн с волновыми числами k = 2 π/ λ в диапазоне Δk в пакете:

Но ведь это не что иное, как соотношение неопределенностей Гайзенберга! Надеюсь, такая проверка удовлетворит самых взыскательных читателей.

3. Наблюдение принципа неопределенности Гайзенберга с пригорка у моря.
Вытекающий из соотношения (3) принцип неопределенности Гайзенберга часто трактуют следующим образом. Если мы попытаемся своим прибором измерить пространственную координату частицы (пакета волн) с погрешностью в пределах Δ х, то в результате такого измерения компонента импульса частицы вдоль той же координаты (компонента волнового числа) станет неопределенной в рамках Δp

1 / Δ х). Продемострируем это утверждение картинкой, которую многие из нас могли наблюдать на берегу моря:

Из этой картинки видно, что если мы ограничиваем (измеряем) волну вдоль координаты, параллельной передней стенке мола, проходом ширины dx, то в том же направлении возникает неопределенность волнового вектора K на величину dk. Что выражается в искривлении фронта вошедшей внутрь мола волны.

4. Волны де Бройля.
Предтечей соотношения неопределенностей Гайзенберга явилась ничуть не противоречащая ему гипотеза де Бройля, предписывающая каждой имеющей массу частице длину волны

Его в качестве шутливого примера можно применить и к идущему по улице человеку. В системе отсчета домов, мимо которых он проходит, длина волны де Бройля человека λ дБ

Источник

ВОЛНОВОЙ ПАКЕТ

Полезное

Смотреть что такое «ВОЛНОВОЙ ПАКЕТ» в других словарях:

ВОЛНОВОЙ ПАКЕТ — занимающее ограниченный объем и перемещающееся в пространстве волновое поле. Волновой пакет может быть разложен на сумму монохроматических волн, частоты которых лежат в определенном интервале; чем уже волновой пакет, тем больше этот интервал. При … Большой Энциклопедический словарь

волновой пакет — цуг волн Последовательность непрерывных упругих волн, исходящих из одного источника и распространяющихся в одном направлении. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное… … Справочник технического переводчика

Волновой пакет — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия

волновой пакет — занимающее ограниченный объём и перемещающееся в пространстве волновое поле. Волновой пакет может быть разложен на сумму монохроматических волн, частоты которых лежат в определенном интервале; чем уже волновой пакет, тем больше этот интервал. При … Энциклопедический словарь

волновой пакет — bangų paketas statusas T sritis radioelektronika atitikmenys: angl. wave packet vok. Wellengruppe, f; Wellenpaket, n rus. волновой пакет, m pranc. groupe d ondes, m … Radioelektronikos terminų žodynas

волновой пакет — banginis paketas statusas T sritis fizika atitikmenys: angl. wave packet vok. Wellengruppe, f; Wellenpaket, n rus. волновой пакет, m pranc. paquet d’ondes, m … Fizikos terminų žodynas

Волновой пакет — распространяющееся волновое поле, занимающее в каждый момент времени ограниченную область пространства. В. п. может возникнуть у волн любой природы (звуковых, электромагнитных и т.п.). Такой волновой «всплеск» в некоторой области… … Большая советская энциклопедия

волновой пакет акустической эмиссии — Механический сигнал, порождаемый единичным актом акустической эмиссии. [ГОСТ 27655 88] Тематики акустические измерения … Справочник технического переводчика

Источник

Волновой пакет

В координатном представлении волны (например, в декартовой системе координат ) положение локальной вероятности физического объекта задается положением пакетного решения. Более того, чем уже пространственный волновой пакет и, следовательно, чем лучше локализовано положение волнового пакета, тем больше разброс импульсов волны. Этот компромисс между спредом позиции и спредом импульса является характерной чертой принципа неопределенности Гейзенберга и будет проиллюстрирован ниже.

Содержание

Историческая справка [ править ]

Идеи квантовой механики продолжали развиваться на протяжении всего ХХ века. Созданная картина представляла собой мир из частиц, в котором все явления и материя состоят из отдельных частиц и взаимодействуют с ними; однако эти частицы описывались волной вероятности. Взаимодействия, местоположения и вся физика будут сведены к расчетам этих амплитуд вероятности.

Базовое поведение [ править ]

Недисперсионный [ править ]

В качестве примера распространения без дисперсии рассмотрим волновые решения следующего волнового уравнения из классической физики

Для упрощения рассмотрим только волны, распространяющиеся в одном измерении (расширение до трех измерений не вызывает затруднений). Тогда общее решение

e^\,dk.>

Фактор 1 / _{√ 2я} происходит от преобразования Фурье конвенции. Амплитуда A (k) содержит коэффициенты линейной суперпозиции плоских волновых решений. Эти коэффициенты, в свою очередь, могут быть выражены как функция от u (x, t), вычисленная при t = 0 путем инвертирования соотношения преобразования Фурье, приведенного выше:

e^<-ikx>\,dx.>

Бездисперсное распространение действительной или мнимой части этого волнового пакета представлено на анимации выше.

Дисперсный [ править ]

Напротив, в качестве примера распространения теперь с дисперсией рассмотрим вместо этого решения уравнения Шредингера (Pauli 2000, где m и ħ установлены равными единице),

что дает дисперсионное соотношение

\psi (x,0)=<\sqrt[<4>]<2>>\exp(<-x^<2>+ik_<0>x>)>

.\end>>

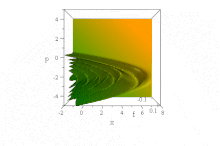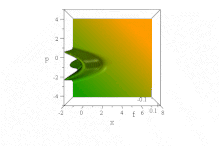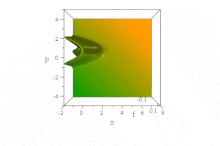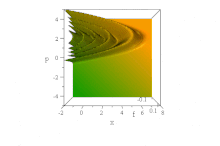
Впечатление о дисперсионном поведении этого волнового пакета получается, если посмотреть на плотность вероятности:

.>

Профиль импульса A (k) остается неизменным. Тока вероятности является

Гауссовские волновые пакеты в квантовой механике [ править ]

Вышеупомянутый дисперсионный гауссовский волновой пакет, ненормализованный и просто центрированный в начале координат, вместо этого, при t = 0, теперь может быть записан в 3D, теперь в стандартных единицах: [3] [4]

Каждая отдельная волна вращается только по фазе во времени, так что решение с преобразованием Фурье с временной зависимостью имеет вид

Обратное преобразование Фурье по-прежнему гауссово, но теперь параметр a стал сложным, и есть общий коэффициент нормализации. [5]

Интеграл Ф во всем пространстве инвариантен, потому что это скалярное произведение Ф с состоянием нулевой энергии, которая является волной с бесконечной длиной волной, с постоянной функцией пространства. Для любого собственного состояния энергии η ( x ) скалярное произведение

Интеграл ∫ | Ψ | 2 d 3 r также является инвариантом, что является утверждением сохранения вероятности. Ясно,

e^ <-\cdot \mathbf \over a^<2>+(\hbar t/m)^<2>>>,>

Поезд волн Эйри [ править ]

\mathrm \left(2^<2>\left(Bx+\over B^<2>>-2Bpt\right)\right).\end>>

В 2018 году совместными усилиями исследователей из израильских, немецких и американских университетов было проведено первое экспериментальное наблюдение кубической фазы ускоряющихся волновых пакетов Эйри. [9]

Бесплатный пропагатор [ править ]

ψ 0 ( x ) = 1 2 π ϵ e − x 2 2 ϵ <\displaystyle \psi _<0>(x)=<1 \over <\sqrt <2\pi \epsilon>>>e^ <-\over 2\epsilon >>\,>

K t ( x ) = 1 2 π ( i t + ϵ ) e − x 2 2 i t + ϵ <\displaystyle K_(x)=<1 \over <\sqrt <2\pi (it+\epsilon )>>>e^ <-x^<2>\over 2it+\epsilon >\,>

Далее обратите внимание, что норма волновой функции бесконечна, что также верно, поскольку квадрат дельта-функции расходится таким же образом.

Фактор, включающий ε, является бесконечно малой величиной, которая нужна для того, чтобы убедиться, что интегралы по K правильно определены. В пределе ε → 0 K становится чисто осциллирующим, и интегралы от K не сходятся абсолютно. В оставшейся части этого раздела он будет установлен в ноль, но для того, чтобы все интегрирования по промежуточным состояниям были четко определены, предел ε → 0 должен приниматься только после вычисления конечного состояния.

В пределе, когда t мало, пропагатор, конечно, переходит к дельта-функции:

,>

но только в смысле распределений : интеграл от этой величины, умноженный на произвольную дифференцируемую пробную функцию, дает значение пробной функции в нуле.

Чтобы убедиться в этом, обратите внимание, что интеграл по всему пространству K всегда равен 1,

так как этот интеграл является скалярным произведением K с однородной волновой функцией. Но фазовый множитель в показателе экспоненты имеет ненулевую пространственную производную везде, кроме начала координат, и поэтому, когда время невелико, есть быстрые сокращения фазы во всех точках, кроме одной. Это строго верно, когда предел ε → 0 берется в самом конце.

она становится колебательной волной,

Теперь, поскольку каждую функцию можно записать как взвешенную сумму таких узких пиков,

Поскольку амплитуду, идущую от x к y по прошествии времени t + t ‘, можно рассматривать в два этапа, пропагатор подчиняется тождеству композиции,

,>

Аналитическое продолжение диффузии [ править ]

,>

где множитель 2, который можно удалить, изменяя масштаб во времени или пространстве, используется только для удобства.

Решением этого уравнения является гауссиан растекания,

,>

и, поскольку интеграл от ρ _t постоянен, а ширина сужается на малых временах, эта функция приближается к дельта-функции при t = 0,

lim t → 0 ρ t ( x ) = δ ( x ) <\displaystyle \lim _\rho _(x)=\delta (x)\,>

опять же только в смысле распределений, так что

lim t → 0 ∫ x f ( x ) ρ t ( x ) = f ( 0 ) <\displaystyle \lim _\int _f(x)\rho _(x)=f(0)\,>

который является оператором бесконечно малой диффузии,

Матрица имеет два индекса, которые в непрерывном пространстве делают ее функцией от x и x ‘. В этом случае, из-за инвариантности перевода, матричный элемент K зависит только от разницы позиций, и удобное злоупотребление обозначениями состоит в том, чтобы ссылаться на оператор, матричные элементы и функцию разности с тем же именем:

Трансляционная инвариантность означает, что непрерывное умножение матриц,

Экспонента может быть определена в диапазоне t s, который включает комплексные значения, при условии, что интегралы по ядру распространения остаются сходящимися,

который иллюстрирует указанную выше эволюцию гауссианов во времени.

Исходя из фундаментальной сущности возведения в степень или интеграции путей,

ψ 0 ( x ) = K a ( x ) = K a ∗ δ ( x ) <\displaystyle \psi _<0>(x)=K_(x)=K_*\delta (x)\,>

составляет состояние, эволюционировавшее во времени,

Это иллюстрирует указанную выше диффузную форму комплексных гауссовских решений,

Источник

Закрученные электроны как портал в квантовый мир

От плоских волн к вихрям

Так что же такое электроны? Точечные заряженные частицы, подверженные влиянию электромагнитного поля (сила Кулона с электрической стороны силы и сила Лоренца с темной магнитной стороны)? Волны вероятности, подчиняющиеся уравнению Шрёдингера? И если заряд электрона точечный, то где он прячется в электронном облаке?

И хотя с вычислительной точки зрения всем ясно что делать, но споры об интерпретациях и философском смысле волновой функции не утихают. Поэтому всегда хорошо, когда до философских вопросов добираются экспериментаторы и начинают измерять корреляции, мощность излучения, силу тока и т.д.

Навскидку можно упомянуть копенгагенскую интерпретацию, ансамблевую, квантовую механику Бома, и многомировую интерпретацию Эверетта. Но споры не утихают, и утихнуть не могут, потому что как-то так получается, что разные интерпретации в экспериментах никак не отличаются.

Однако наиболее интересные и общие формы появляются, начиная с трехволновой интерференции. А именно, волновые поля, состоящие из трех или более интерферирующих плоских волн, обычно содержат фазовые сингулярности, т.е. дислокации фазовых фронтов или вихрей. Такие особенности возникают в точках деструктивной интерференции, где амплитуда волновой функции обращается в нуль, а фаза является неопределенной.

Фазовые сингулярности для волн на плоскости. Bliokh, K. Y., Ivanov, I. P., Guzzinati, G., Clark, L., Van Boxem, R., Béché, A., & Verbeeck, J. (2017). Theory and applications of free-electron vortex states. Physics Reports, 690, 1-70.

Способы закручивания электронов. Bliokh, K. Y., Ivanov, I. P., Guzzinati, G., Clark, L., Van Boxem, R., Béché, A., & Verbeeck, J. (2017). Theory and applications of free-electron vortex states. Physics Reports, 690, 1-70.

Излучение Смита-Парселла

25 сентября 1953 года Стивен Смитт, студент недавно получившего нобелевку за открытие ядерного магнитного резонанса Эдварда Парселла, вместе со своим шефом направили для публикации короткое письмо о наблюдении видимого излучения при взаимодействии пучка электронов с дифракционной решеткой. Физический механизм этого излучения связан с поляризацией материала дифракционной решетки и возникновением наведенных токов, когда рядом пролетает заряженная частица. Эти наведенные токи и есть источник излучения. Поскольку эти источники излучения располагаются периодично вдоль решетки, некоторые волны в точке наблюдения будут складываться и усиливать друг друга. Нужно только чтобы у них фаза была одинакова. Простую формулу для длины волны излучения Смита-Парселла мог бы вывести еще Гюйгенс

Научные статьи могут быть весьма короткими и понятными

Квантовая задача и квазиклассический предел

Расплывание и редукция волновых пакетов

Еще один важный момент заключается в том, что свободно летящий волновой пакет должен расплываться.

По мере расплывания информация о положении электрона становится размытой

Причем, чем сильнее начальный пакет сконцентрирован, тем быстрее будет расплываться. Это связано с принципом неопределенности Гейзенберга. Если пакет был четко ограничен, значит разброс импульсов был велик. Поэтому очень быстро вероятность найти электрон будет размазана по всему пространству. Как правило, работают в параксиальном приближении, когда на интересующем нас интервале времени волновой пакет почти не расплывается. Но для закрученного электрон время расплывания будет обратно пропорционально угловому моменту. Грубо говоря, пакет будет быстрее расплываться в плоскости вихря, как если бы его разбрасывало центробежной силой. Ускорение расплывания для сильно закрученных электронов означает, что его можно «увидеть», например, за время пролета над решеткой, во время формирования излучения Смита-Парселла.

Кстати, из-за того, что вдоль оси вихра расплывание будет идти в нормальном темпе, квадрупольный момент волнового пакета будет со временем возрастать. Еще, у такого пакета будет дипольный магнитный момент. Для любителей аналитических вычислений это идеальный объект приложения своих умений. Возьмем закрученный электрон в виде волнового пакета Гаусса-Лагерра, с заданной средней скоростью и начальными размерами, пролетающий над решеткой. Выглядеть это будет как расширяющееся колечко дыма. Можно получить точную формулу для мультипольных моментов, найти воздействующее на решетку поле, найти токи и вычислить интенсивность излучения в заданном направлении на большом расстоянии.

Закрученный электрон пролетает над дифракционной решеткой.

Захлопавшая при этих словах морская свинка была немедленно подавлена судейскими властями. «Подавлена» — слово трудное, и я сейчас вам объясню, что они сделали: у них был большой холщовый мешок с завязками, они засунули туда морскую свинку вниз головой и уселись сверху.

Получается, что в нашей задаче размер пакета строго меньше длины излучения. Это важно и интересно. Поскольку наблюдая излученный фотон в микроскоп, можно было бы сказать где же над решеткой находится электрон. И тогда, все эти волновые тонкости исчезли бы. Но в данном случае этого скорее всего не произойдет, так как волновая функция итак сконцентрирована в области меньшей чем длина волны. Я пишу скорее всего, потому что, а вдруг?

Схема неразрушающего измерения расплывания закрученного электрона

Закрученный электрон, летящий вдоль решетки будет вызывать излучение наведенное зарядом, магнитным моментом и электрическим квадрупольным моментом. Квадрупольный момент растет как квадрат пройденного расстояния. Поскольку излучение от каждой полоски решетки складывается, мы интегрируем квадрат и получаем куб. Получается, что решетка резонансно усиливает излучение от квадрупольного момента. В целом это приведет к тому, что линия излучения Смита-Парселла от закрученного пакета будет чуть ярче, чем от обычного пакета. И эффект даже не маленький. Но, конечно, трудно его выделить на фоне других эффектов (изменение импакт-параметра меняет яркость еще сильнее).

Хотя, не все так безнадежно. Полная интенсивность излучения от обычных пакетов должна линейно расти с длиной решетки, а вот для закрученных возникнет нелинейный (кубический рост). Может такой эффект и получится поймать? Конечно, речь здесь идет о том, что над решеткой пролетит много пакетов, вылетевших из одного источника, и будет собрана большая статистика излученных фотонов. Но если для закрученных электронов будет наблюдаться кубический рост интенсивности с длиной решетки, то это можно интерпретировать, как «размазанность» заряда по всему кольцу закрученного пакета и экспериментальное детектирование расплывания. Важно, что статистика излучения собранная от точечных электронов, в среднем за много пролетов над решеткой заполняющих такой же бублик будет отличаться.

Сравнение зависимости яркости излучения от длины решетки для обычных и закрученных пакетов.

Или угол на котором наблюдается максимум излучения тоже зависит от структуры пакета.

Зависимость яркости излучения от полярного угла.

По моим скромным соображениям, узнать есть ли у электронов пролетающих над решеткой квадрупольный момент, можно, если рассматривать не только параллельный пролет, но и изменять угол пролета. Это почти эквивалентно изменению длины решетки. Тогда можно не менять источник электронов и решетку, а это сделает задачу экспериментатора проще. Я уже посчитал, что будет происходить в этом случае, но наверное это уже материал для следующей заметки.

Эпилог

Однако и более ранний эксперимент [6] где изучалось непосредственное взаимодействие фотонов с пакетами увидел только точечные заряды. Значит, хотя электрон и волна-частица, но заряд электрона только частица?

Литература

Bliokh, K. Y., Ivanov, I. P., Guzzinati, G., Clark, L., Van Boxem, R., Béché, A., & Verbeeck, J. (2017). Theory and applications of free-electron vortex states. Physics Reports, 690, 1-70.

S. J. Smith and E. Purcell, Physical Review 92, 1069 (1953).

Karlovets, D. V., and A. M. Pupasov-Maksimov. «Nonlinear quantum effects in electromagnetic radiation of a vortex electron.» Physical Review A 103.1 (2021): 012214.

Pupasov-Maksimov, Andrey, and Dmitry Karlovets. «Smith–Purcell radiation of a vortex electron.» New Journal of Physics 23.4 (2021): 043011.

Remez, Roei, et al. «Observing the quantum wave nature of free electrons through spontaneous emission.» Physical review letters 123.6 (2019): 060401.

M. Ware, E. Cunningham, C. Coburn, and J. Peatross, Measured photoemission from electron wave packets in a strong laser field, Opt. Lett. 41, 689 (2016).

Источник