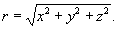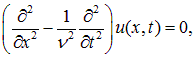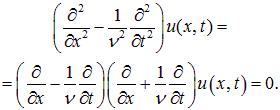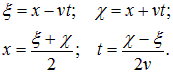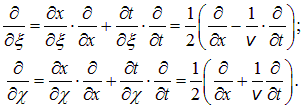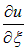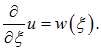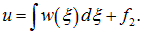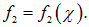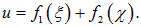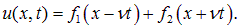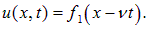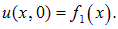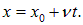что такое волновое уравнение
Что такое волновое уравнение
Волновое уравнение
Wave equation
Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением
где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид
Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T
Частота ω и период колебаний T связаны соотношением
Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x
u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).
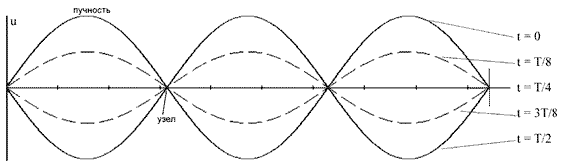
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.
Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.
| Падающая волна | u1 = Asin(ωt + kx) | |
| Отражённая волна | u2 = Asin(ωt − kx + π) | |
| Стоячая волна | u1 + u2 = A(x)cosωt | (2) |
Соотношение (2) можно получить, используя формулу
sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]
и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.
Волновое уравнение
Что такое волновое уравнение
Волновое уравнение — линейное гиперболическое уравнение в частных производных, описывающее колебательные процессы в сплошных средах и электромагнетизме:
Где \(\triangle\) — оператор Лапласа, u=u(x,t) — дифференцируемая функция, \(x\in\mathbb
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Волновые уравнения в математической физике применяются для описания малых поперечных колебаний струны и мембраны, акустических процессов в газообразных, жидких и твёрдых средах, электромагнитных и гравитационных волн.
Общий вид
Составляющие уравнения
При работе с физическими процессами в трёхмерном пространстве волновое уравнение получается из уравнения плоской волны.
Если мы имеем уравнение плоской волны:
\(A(\overrightarrow r,\;t)\;=\;A_0\cos(wt\;-\;(\overrightarrow k,\overrightarrow r)\;+\;\varphi_0)\)
Где \(A(x,\;t)\;\) — возмущение в точке x в момент времени t, \(A_0\) — волновая амплитуда, \(\omega\) — круговая частота, \(\overrightarrow k\) — волновой вектор, \(\overrightarrow k\;=\;\overrightarrow k(x,y,z)\) — радиус-вектор в точке \(x, y, z, \varphi_0\) — начальная фаза колебаний.
Если мы продифференцируем его по переменным x, y, z и t, то получим систему уравнений в частных производных:
При сложении уравнений (2), (3), (4) получаем:
Из уравнений (1) и (5) следует, что:
Таким образом, мы получаем общее волновое уравнение из суммы уравнений плоской волны в частных производных.
Для уравнений в n-мерных пространствах для построения берется система дифференциальных уравнений в частных производных по времени t и по каждому из n измерений.
Для одномерного пространства данное уравнение называется уравнением колебания струны и имеет следующую характеристику:
Из описанного выше мы можем сделать вывод, что в общем случае для решения волновых задач необходимо применение численных методов. Тем не менее, для некоторых случаев существуют аналитические решения уравнений.
Операторы уравнения
С применением оператора Лапласа уравнение (7) принимает привычный нам вид:
Оператором Д’Аламбера \(\square\) называется следующая разность:
Тогда волновое уравнение можно представить в виде:
Решение уравнения
В математической физике существуют несколько частных случаев волновых уравнений, для которых существуют аналитические решения:
Формула Д’Аламбера
Рассмотрим формулу Д’Аламбера, являющейся частным случаем волновых уравнений в одномерном пространстве:
Где f=f(x,t) — вынуждающая внешняя сила, \(u(x,0)\;=\;\varphi(x),\;u_t(x,0)=\psi(x)\) — начальные условия.
Тогда решение формулы Д’Аламбера имеет вид:
Формула Пуассона-Парсенваля
Частным случаем волнового уравнения для поверхности или плоскости является формула Пуассона-Парсенваля.
Где \(u(x,0)=\varphi(x),\;u_t(x,0)=\psi(x)\) — начальные условия.
Тогда решение формулы Пуассона-Парсенваля имеет следующий вид:
Где \(u=u(x,t), f=f(x,t), u,\;f\;\in\mathbb
Мы получим следующее решение уравнения:
\(u(x,t)\;=\;\frac\partial<\partial t>\left[\frac1<4\mathrm<πa>^2\mathrm t>\iint\limits_S\varphi_0(y)d^2S_n\right]+\frac1<4\mathrm<πa>^2\mathrm t>\iint\limits_S\varphi_1(y)d^2S_n+\frac1<4\mathrm<πa>^2>\underset
Где \(S:\;\vert x-y\vert=at \) — сфера, по которой осуществляется интегрирование.
Решение в сферических координатах
Стандартное волновое уравнение в сферических координатах имеет следующий вид:
Требуется найти решение данного в обычной форме:
Используя в изначальном уравнении данную формулу, а также воспользовавшись методом разделения переменных, получаем:
Посредством преобразований получаем следующую систему уравнений:
Тогда, для любых \(\lambda_n=n(n+1),\;n\in\mathbb
Для удобства дальнейших вычислений произведём замену функции f(r) на R(r):
Где \(R_n(r)=Z_
Тогда мы получаем следующее выражение:
Волновое уравнение механических волн
Механические волны — упругие возмущения, распространяемые в упругой среде.
Рассматривают поперечные и продольные механические волны.
В продольных волнах колебания, несущие эту волну, осуществляется по вектору, параллельном направлению движения. Они возможны в газообразной, жидкой и твёрдой среде. Особенностью поперечных волн является возможность их наличия исключительно при возможности деформации сдвига в твёрдых средах.
В условиях распространения в бесконечной натянутой струне поперечная монохроматическая волна может быть описана следующим выражением (уравнением бегущей струны):
\(\xi(t,z)=A\cdot\cos\omega(t-\frac zv) (23)\)
Где \(\xi(t,z)\) — смещение частицы из положения равновесия в струне, z — расстояние от начала струны до точки равновесного положения частицы в струне, v — скорость распространения колебаний.
Примеры задач и решение
Найти скорость распространения звуковой волны, если частота колебаний равна \(\nu\) =400Гц, а амплитуда \(A=10^<-4>м\) и длина волны \(\lambda\) =0,8м. Также определить максимальную скорость частиц в данной среде.
Ввиду недостаточно строгого определения условий, сделаем допущение, что волна является плоской.
Тогда, сориентировав ее распространение по оси X, получим следующее уравнение:
Зная, что длина волны равна \(\lambda=\frac v\nu,\) получаем, что скорость волны равна:
Исходя из того, что скорость есть первая производная расстояния по времени, имеем:
\(\frac
Скорость распространения волны по упругой струне составляет \(\nu\) =10 м/с. Амплитуда колебаний точек в струне составляет A=0,05 м, период колебаний составляет Т=1 с. Сформулировать уравнение волны.
Так как в общем случае при распространении по оси X уравнение поперечной механической волны имеет вид:
то, найдя циклическую частоту по формуле \(\omega=\frac<2\pi>T=2\pi\;(рад/с),\) получаем:
\(\xi(t,z)=0,05\cdot\cos2\pi(t-\frac x10) (м)\)
Ответ: \(\xi(t,z)=0,05\cdot\cos2\pi(t-\frac x10)\) м.
Волновое уравнение
Полезное
Смотреть что такое «Волновое уравнение» в других словарях:
Волновое уравнение — в математике линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно… … Википедия
ВОЛНОВОЕ УРАВНЕНИЕ — в механике, линейное однородное дифф. ур ние в частных производных, описывающее распространение волн в среде; имеет вид: где t время, х, у, z пространственные декартовы координаты, W= W(х, у, z, t) ф ция, характеризующая возмущение среды в точке… … Физическая энциклопедия
ВОЛНОВОЕ УРАВНЕНИЕ — дифференциальное уравнение с частными производными 2 го порядка, описывающее процесс распространения возмущений в некоторой среде. Напр., малые колебания натянутой струны описываются волновым уравнением где u(х,t) искомая функция отклонение… … Большой Энциклопедический словарь
Волновое уравнение — линейное в частных производных второго порядка уравнение с постоянными коэффициентами, описывающее распространение в среде возмущений с постоянной скоростью. При выводе В. у. из уравнений газовой динамики пренебрегают вязкостью и объёмными силами … Энциклопедия техники
волновое уравнение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN wave equation … Справочник технического переводчика
волновое уравнение — banginė lygtis statusas T sritis fizika atitikmenys: angl. wave equation vok. Wellengleichung, f rus. волновое уравнение, n pranc. équation de l’onde, f; équation d’onde, f … Fizikos terminų žodynas
ВОЛНОВОЕ УРАВНЕНИЕ — уравнение с частными производными вида описывающее различные колебательные процессы и процессы распространения волн. Для В. у., являющегося уравнением гиперболич. типа, обычно ставятся две задачи: Коши задача и смешанная задача. Классич. решением … Математическая энциклопедия
волновое уравнение — волновое уравнение линейное в частных производных второго порядка уравнение с постоянными коэффициентами, описывающее распространение в среде возмущений с постоянной скоростью. При выводе В. у. из уравнений газовой динамики пренебрегают… … Энциклопедия «Авиация»
волновое уравнение — волновое уравнение линейное в частных производных второго порядка уравнение с постоянными коэффициентами, описывающее распространение в среде возмущений с постоянной скоростью. При выводе В. у. из уравнений газовой динамики пренебрегают… … Энциклопедия «Авиация»
Волновое уравнение
Смотреть что такое «Волновое уравнение» в других словарях:
Волновое уравнение — в математике линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно… … Википедия
ВОЛНОВОЕ УРАВНЕНИЕ — в механике, линейное однородное дифф. ур ние в частных производных, описывающее распространение волн в среде; имеет вид: где t время, х, у, z пространственные декартовы координаты, W= W(х, у, z, t) ф ция, характеризующая возмущение среды в точке… … Физическая энциклопедия
ВОЛНОВОЕ УРАВНЕНИЕ — дифференциальное уравнение с частными производными 2 го порядка, описывающее процесс распространения возмущений в некоторой среде. Напр., малые колебания натянутой струны описываются волновым уравнением где u(х,t) искомая функция отклонение… … Большой Энциклопедический словарь
волновое уравнение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN wave equation … Справочник технического переводчика
волновое уравнение — banginė lygtis statusas T sritis fizika atitikmenys: angl. wave equation vok. Wellengleichung, f rus. волновое уравнение, n pranc. équation de l’onde, f; équation d’onde, f … Fizikos terminų žodynas
ВОЛНОВОЕ УРАВНЕНИЕ — уравнение с частными производными вида описывающее различные колебательные процессы и процессы распространения волн. Для В. у., являющегося уравнением гиперболич. типа, обычно ставятся две задачи: Коши задача и смешанная задача. Классич. решением … Математическая энциклопедия
Волновое уравнение — дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде. В случае малых возмущений и однородной изотропной среды В. у. имеет вид: где х, у, z пространственные… … Большая советская энциклопедия
волновое уравнение — волновое уравнение линейное в частных производных второго порядка уравнение с постоянными коэффициентами, описывающее распространение в среде возмущений с постоянной скоростью. При выводе В. у. из уравнений газовой динамики пренебрегают… … Энциклопедия «Авиация»
волновое уравнение — волновое уравнение линейное в частных производных второго порядка уравнение с постоянными коэффициентами, описывающее распространение в среде возмущений с постоянной скоростью. При выводе В. у. из уравнений газовой динамики пренебрегают… … Энциклопедия «Авиация»
2.2. Решение волнового уравнения
Уравнение типа (2.2), описывающее колебания различных упругих сред, называется волновым уравнением. Запишем его формально в виде:
Введем теперь вместо (x, t) новые переменные:
Производные по новым переменным выражаются по стандартным правилам дифференцирования сложной функции:
Отсюда следует, что уравнение (2.16) в новых переменных записывается в виде:
Поскольку производная по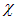 
равна нулю,
не зависит от этой переменной и, следовательно, является некоторой функцией w только от переменной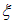 
:
Интегрируем теперь это уравнение:
Первое слагаемое в правой части является только функцией переменной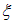 
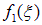
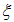
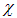
, которую мы обозначим как 
. Второе слагаемое — постоянная интегрирования. Она не зависит от 
, являясь, стало быть, функцией только переменной 
:
Мы получили, что решение волнового уравнения имеет вид:
Подставляя сюда выражения (2.17), мы возвращаемся к прежним переменным (x, t):
Функции f1 и f2 — совершенно произвольны и должны быть определены из начальных и граничных условий.
Обсудим физический смысл полученных решений. Ограничимся сначала первым слагаемым. Пусть
В момент времени t = 0 функция f1(x) задает распределение смещений (профиль струны, деформацию твердого тела, распределение давления или частиц в газе и т. д.):
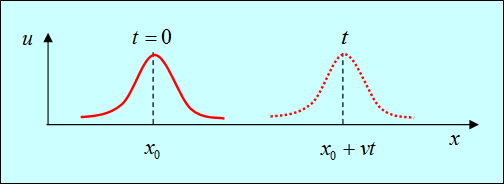
Предположим, например, что это распределение имеет максимум в точке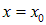 
(рис. 2.6).
Такое распределение называют обычно волновым пакетом. В момент t максимум функции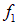 
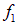
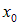
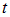
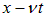
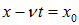
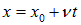
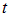
по-прежнему будет в точке, в которой аргумент 
равен 
, но теперь (в момент времени 
) аргумент равен 
, таким образом: 
или 
. Другими словами, за время от 0 до 
волновой пакет сдвинется вправо на расстояние vt, так что максимум теперь придется на точку
Нетрудно сообразить, что форму свою волновой пакет при этом перемещении не изменит.
Мы видим, что начальное распределение движется вправо со скоростью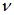 
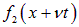
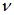
. Аналогично, второе слагаемое, 
, описывает движение волнового пакета налево с той же скоростью . Общее решение (2.21) является суперпозицией двух этих решений.
В свою очередь, любой волновой пакет может быть представлен как суперпозиция гармонических функций. Отсюда — особая роль решений волнового уравнения вида:
Это решение описывает монохроматическую волну, распространяющуюся направо со скоростью