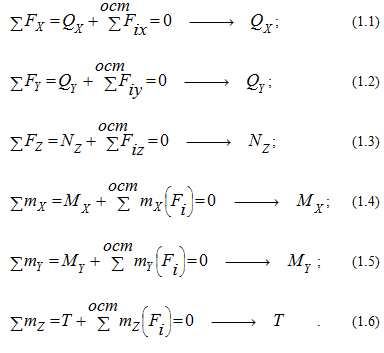что такое внутренний силовой фактор

Сопромат online

Расчеты в режиме online

1.3. Метод сечений. Внутренние силовые факторы.

Целостность твердого тела, его форма обусловливаются на­личием сил взаимодействия между его частицами. При дефор­мации тела под действием внешних нагрузок и других внеш­них воздействий происходит изменение сил взаимодействия между частицами тела. Эти изменения сил взаимодействия в сопротивлении материалов называются внутренними силами. Таким образом, под внутренними силами необходимо пони­мать силы взаимодействия между частицами тела, возника­ющие только в результате деформации тела. При отсутствии де­формации внутренние силы в теле считаются равными нулю.

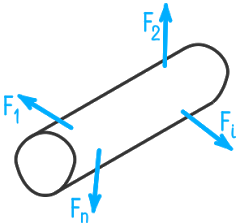
Для определения внутренних сил необходимо, используя метод сечений, перевести их в категорию сил внешних. На рисунке 1 представлено твердое тело, на которое действует про­извольная система внешних сил F₁, F₂….F_n, удовлетворя­ющая условиям равновесия. Мысленно рассечем тело плоскостью на две части и отброс им одну часть.

Рисунок 1.2 Произвольная система сил.

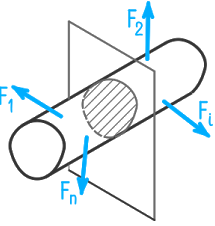
Чтобы любая часть, например левая, находилась в равнове­сии, необходимо действие отброшенной правой части на рас­сматриваемую левую заменить в сечении внутренними силами. В другом сечении они будут другими. Внутренние силы всегда взаимны: правая часть действует на левую так же, как левая на правую. Внутренние силы считаются поверхностными, т.е. принимается, что взаимодействие частиц, примыкающих с раз­ных сторон к сечению, является контактным и что частицы, расположенные за сечением, во взаимодействии не участвуют.

Метод сечений — это прием, позволяющий обнаруживать внутренние силы и рассматривать их как внешние силы по от­ношению к оставшейся (рассматриваемой) части тела.

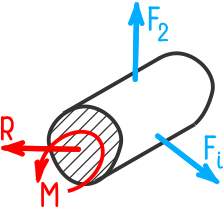
Приведем систему внутренних сил, используя положения статики, к центру тяжести сечения (рисунок 1.3 а).

Рисунок 1.3.а Внутренние силы, приведенные к центру тяжести сечения.

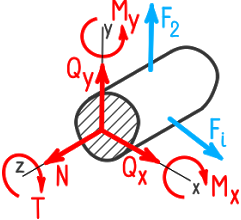
В результате приведения получим главный вектор Fc и главный момент Мс, разложив которые по осям координат, получим три силы и три момента Fх, Fу, Fz, Мх, Му, Мz (рисунок 1.3 б).

Рисунок 1.3.б Внутренние силовые факторы.

Эти составляющие обозначаются специальными буквами и на­зываются внутренними силовыми факторами. F_x = N- назы­вается продольной или нормальной силой; F_z =Q_Z и F_y=Q_y назы­ваются поперечными силами; М_х = Т называется крутящим мо­ментом; М_у и M_z называются изгибающими моментами относи­тельно осей у и z.

Для отсеченной части в общем случае можно составить шесть уравнений равновесия :

Согласно (1.8) нормальная сила N в поперечном сечении равна алгебраической сумме проекций на ось x всех внешних сил, действующих на отсеченную часть тела; поперечные силы Q_y и Q_z в сечении — соответственно равны алгебраической сумме проекций на оси у и z, расположенные в рассматриваемом се­чении, всех внешних сил, действующих на отсеченную часть тела; крутящий момент Т в поперечном сечении равен алгебра­ической сумме моментов относительно оси х всех внешних сил, действующих на отсеченную часть тела; изгибающие мо­менты М_у и М_z в сечении соответственно равны алгебраиче­ской сумме моментов относительно осей у и z рассматриваемо­го сечения всех внешних сил, действующих на отсеченную часть тела. Результаты будут одинаковыми независимо от того, какая отсеченная часть тела рассматривается.

Таким образом, в расчетных схемах как внешние нагрузки, так и внутренние силовые факторы нужно рассматривать как скалярные величины.

Нормальная сила, направленная от сечения, вызывает в се­чении растяжение материала и считается положительной, а на­правленная к сечению — вызывает в сечении сжатие материала и считается отрицательной.

Поперечная сила считается положительной, если внешние силы стремятся вращать отсеченную часть тела (бруса или ра­мы) относительно проведенного сечения по часовой стрелке; если — против часовой стрелки, то поперечная сила считается отрицательной.

Крутящий момент в сечении считается положительным, ес­ли при взгляде на сечение со стороны внешней нормали внеш­ние силы стремятся вращать отсеченную часть по часовой стрелке, если — против часовой стрелки, то крутящий момент в сечении считается отрицательным.

Изгибающий момент от внешних сил, вызывающих сжатие верхних волокон балки или сжатие наружных волокон рамы, считается положительным, а от внешних сил, вызывающих сжа­тие нижних волокон балки или внутренних волокон рамы, — от­рицательным.

Нагружение называется простым, если в поперечных сече­ниях элемента конструкции возникает только один внутрен­ний силовой фактор, или сложным (комбинированным), если в поперечных сечениях элемента одновременно действуют не­сколько внутренних силовых факторов.

Внутренние силовые факторы вдоль элемента (бруса) изме­няются. Эпюрами называются графики, показывающие, как из­меняются внутренние силовые факторы в сечениях по длине бруса (балки). (Пример построения эпюр ступенчатого стержня)

Эпюры позволяют установить положение опасного сече­ния, в котором действуют максимальные внутренние силы и моменты.

Источник

Внутренние силовые факторы — справочник

Привет! Этот справочник, на портале – SoproMats, будет по внутренним силовым факторам при различных видах деформаций: растяжении и сжатии, кручении и изгибе. По каждому фактору будет написана специальная статья, где расскажем, как обозначается, в чем измеряется и как рассчитывается. Для подробного изучения каждого силового фактора, перемещайтесь по указанным гиперссылкам.

ВСФ при растяжении и сжатии

Как известно, при растяжении и сжатии (центральном) возникает один единственный внутренний силовой фактор – продольная сила. В указанной статье рассказывается, что это за сила, в чем измеряется и т.д.

Если вкратце рассказывать, то продольная сила рассчитывается методом сечений, который предполагает, что если вся конструкций находится в равновесии, то и отдельные ее части также будут находится в равновесии, если действие частей друг на друга заменить силовыми факторами.

ВСФ при кручении

При кручении, также как при растяжении и сжатие, в поперечных сечениях действует один силовой фактор – крутящий момент. В статье рассказывается об данном факторе, как он рассчитывается, в каких расчетах используется и как обозначается.

ВСФ при поперечном изгибе

При поперечном изгибе, чаще всего, в сечениях возникают два силовых фактора – поперечная сила и изгибающий момент. Поперечная сила, как правило, используется в проверочном расчете на прочность по касательным напряжениям, а также служит вспомогательным инструментов для определения экстремумов на эпюре изгибающих моментов.

Изгибающий момент используется при проведения прочностных расчетов по нормальным напряжениям. Подробнее об данных величинах можете узнать, перейдя по указанным ссылочкам.

Источник

iSopromat.ru

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.

По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:

надо мысленно рассечь брус, находящийся в равновесии, на две части

и рассмотреть равновесие одной из них.

Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.

Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.

Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

Правила знаков для внутренних силовых факторов

Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:

Эпюры внутренних силовых факторов

В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник