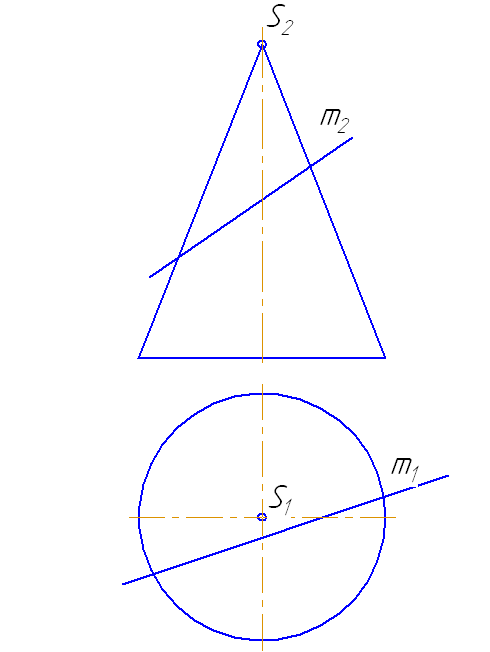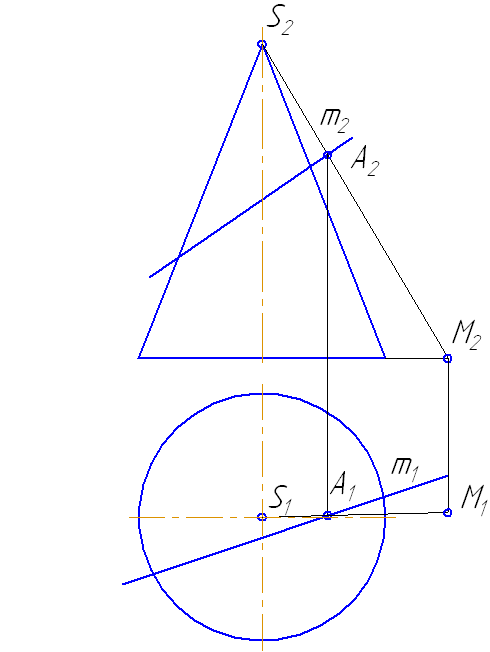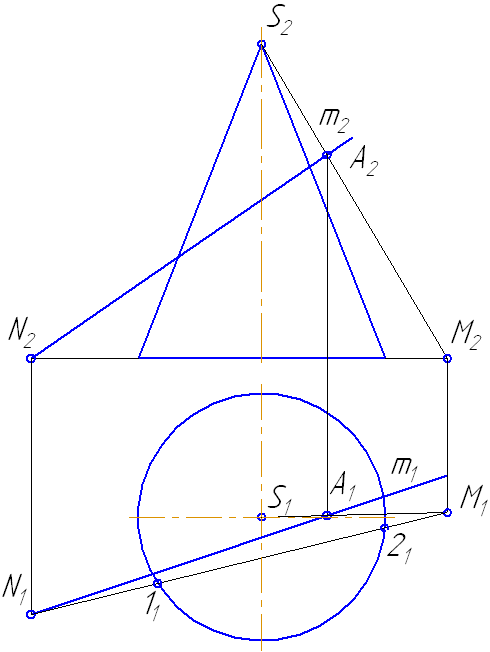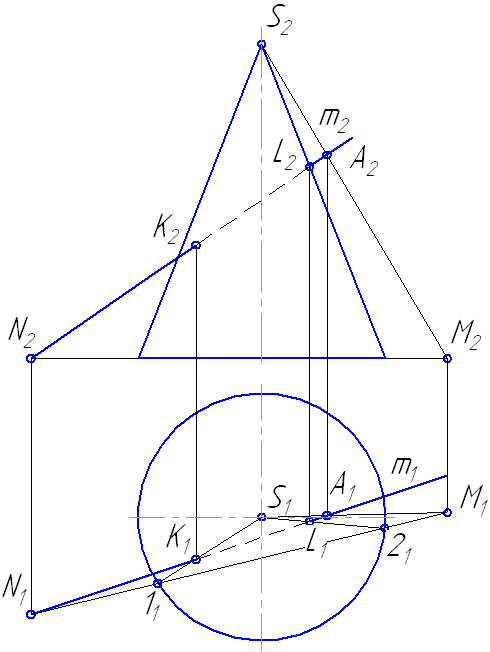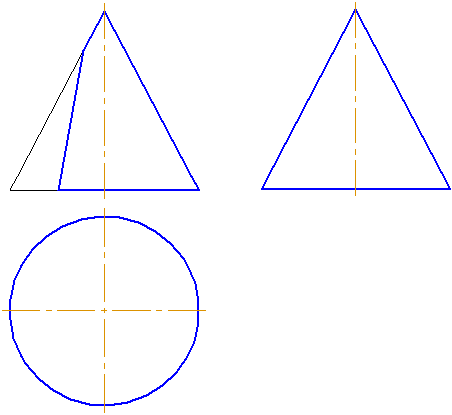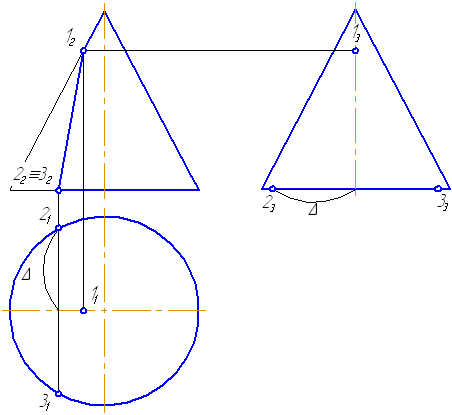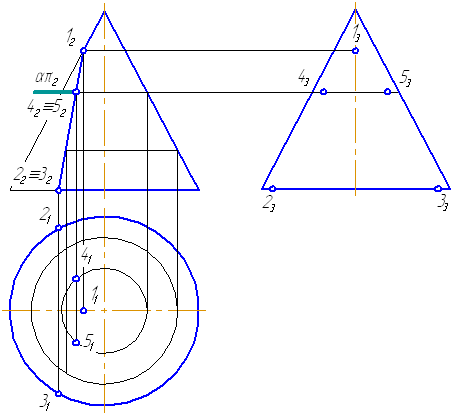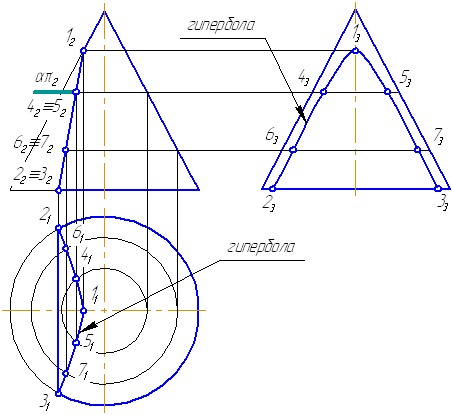что такое вершина в черчении

§ 12. Проекции вершин, ребер и граней предмета

12.1. Как изображают элементы предметов. Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребра, грани, кривой поверхности и т. п. (рис. 85). Поэтому изображение любого предмета сводится к изображению его вершины, ребер, граней и кривых поверхностей.

Рис. 85. Элементы поверхности предмета

Рассмотрим этот процесс на примере построения прямоугольных проекций предмета (рис. 86).

Расположим предмет в пространстве так, чтобы каждая из двух параллельных между собой граней была параллельна одной из плоскостей проекций. Тогда эти грани изобразятся на соответствующих плоскостях проекций без искажения.

Проведем через вершины предмета проецирующие лучи, перпендикулярные плоскостям проекций, и отметим точки пересечения их с плоскостями V, H и W.

Предмет так расположен относительно плоскостей проекций, что на одном проецирующем луче оказалось по две вершины, поэтому их проекции слились в одну точку. Так, вершины А и В лежат на одном луче, перпендикулярном горизонтальной плоскости проекций H. Их горизонтальные проекции а и b совпали. Вершины А и С лежат на одном луче, проецирующем эти точки на фронтальную плоскость проекций. Их фронтальные проекции а’ и с’ также совпали. На профильной плоскости проекций W в одну точку (b» и d») спроецпронались вершины В и D.

Из двух совпадающих на изображении точек одна является изображением видимой вершины, другая — закрытой (невидимой). На горизонтальмой проекции будет видима та вершина, которая расположена в пространстве выше. Так, вершина А видима, вершина В невидима. На фронтальной проекции видимой будет та вершина, которая находится ближе к нам. Отсюда а’ изображение видимой вершины А, с’ — изображение невидимой вершины С, она закрывается при проецировании вершиной А. На изображении обозначение проекций невидимых точек берут иногда в скобки.

Соединив попарно точки на фронтальной, горизонтальной и профильной проекциях, получим изображения ребер предмета. Например, ас — горизонтальная проекция ребра АС, а’b’ фронтальная проекция ребра АB

Рис. 86. Изображения предмета

На рисунке 86 видно, что если ребро параллельно плоскости проекций, то оно на этой плоскости изображается без искажения, или, как говорят, в истинную (натуральную) величину. В этом случае проекция ребра и само ребро равны между собой. Например, проекция а’b’ — истинная величина ребра АВ на фронтальной, а проекция а»b»— на профильной плоскости проекций.

Если ребро перпендикулярно плоскости проекций, оно проецируется на нее в точку. Так, на фронтальную плоскость проекций в точку спроецировалось ребро АС, на горизонтальную плоскость—ребро АВ, на профильную — ребро BD и т. д.

Построив проекции ребер, видим, что на изображении они ограничивают проекции граней. Как и ребро, грань, параллельная плоскости проекций, проецируется на нее без искажения. Например, на профильную плоскость проекций без искажения спроецировалась грань, в которой лежат точки А, В и С. На горизонтальную плоскость проекций спроецировались без искажения нижняя и верхняя грани и т. д. Найдите эти грани на чертеже предмета в системе прямоугольных проекций.

Если грань перпендикулярна плоскости проекций, она проецируется на нее в отрезок прямой.

Таким образом, каждый отрезок прямой на изображении — это проекция ребра или проекция плоскости, перпендикулярной плоскости проекций. Ребра и грани предмета, наклоненные к плоскости проекций, проецируются на нее с искажением. Найдите такие ребра и грань на рисунке 86.

Строя чертеж, надо четко представлять, как изобразится на нем каждая вершина, ребро и грань предмета. Читая чертеж, надо представить, изображение какой части предмета скрыто за каждой точкой, отрезком или фигурой.

Следует помнить, что каждый вид— это изображение всего предмета, а не одной его стороны. Разница заключается лишь в том, что одни грани спроецируются в истинную фигуру, другие— в отрезки прямых.

1. В каком случае на изображении проекции точек совпадают? Какая из двух точек, проекции которых на горизонтальной плоскости совпали, будет видимой?

2. В каком случае отрезок прямой (ребро) проецируется в истинную величину? в точку?

3. В каком случае грань (часть плоскости) проецируется в отрезок прямой? В каком случае она спроецируется в истинную величину?

Рис. 87. Задания для упражнений

Рис. 88. Изображение элементов поверхности детали

3. На рисунке 88 грани предмета выделены цветом. Обозначьте вершины буквами или цифрами. Проанализируйте, как расположены грани предмета относительно плоскостей проекций. Ответ запишите в рабочей тетради.

4. Перечертите или перенесите на кальку рисунок 89 и выделите на всех проекциях соответствующие грани тем же цветом, что и на наглядных изображениях.

Рис. 89. Задания для упражнений

5. На рисунке 90 даны изображения трех предметов. Проекции их граней обозначены буквами. Напишите, как расположены в каждом случае относительно фронтальной плоскости проекций эти грани. Пример записи: А — параллельно, Б — перпендикулярно, В — наклонно.

Рис. 90. Задания для упражнений

12.2. Построение проекций точек на поверхности предмета. Теперь рассмотрим способы построения проекций точек, лежащих на поверхностях предметов.

На рисунке 91 изображена шестиугольная пирамида. На линии, являющейся проекцией ребра, задана фронтальная проекция а точки А. Как найти ее остальные проекции?

Рис. 91. Построение проекций точки, лежащей на ребре пирамиды

Рассуждают так. Точка находится на ребре предмета. Проекции точки должны лежать на проекциях этого ребра. Следовательно, нужно сначала найти проекции ребра, а затем при помощи линий связи отыскать проекции точки.

Чтобы построить профильную проекцию предмета и, в частности, профильную проекцию ребра, на котором находится точка А, удобно воспользоваться постоянной прямой. Так называют линию, которую проводят справа от вида сверху под углом 45° к рамке чертежа (рис. 91). Линии связи, идущие от вида сверху, доводят до постоянной прямой. Из точек их пересечения проводят перпендикуляры к горизонтальной прямой и строят профильную проекцию.

Рис. 92. Построение постоянной прямой

Расположение постоянной прямой определяет место строящегося вида (рис. 91). Но если три вида уже построены, как на рисунке 92, а, нужно найти точку, через которую пройдет постоянная прямая. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии. Через полученную точку k (рис. 92, б) проводят прямую под углом 45° к осям. Это и будет постоянная прямая.

Если осей симметрии на чертеже нет, то продолжают до пересечения в точке k₁ горизонтальную и профильную проекции граней, проецирующихся в виде отрезков прямых. Через точку k₁ проводят постоянную прямую.

А теперь вернемся к рисунку 91. Проекции ребра, на котором лежит точка А, выделены голубым цветом. Горизонтальная проекция точки А должна лежать на горизонтальной проекции ребра. поэтому проводим из точки а’ вертикальную линию связи. В месте ее пересечения с проекцией ребра находится точка а — горизонтальная проекция точки А.

Профильная проекция а» точки А лежит на профильной проекции ребра. Ее можно определить и как точку пересечения линий связи.

Мы рассмотрели, как находят на чертеже проекции точек, лежащих на ребрах предметов. Однако часто приходится строить проекции точек, лежащих не на ребрах, а на гранях. Например, чтобы просверлить в детали отверстие, надо определить, где находится его центр.

Чтобы по одной проекции точки, лежащей на грани предмета, найти остальные, нужно прежде всего найти проекции этой грани. Такие упражнения вы уже выполняли (см. рис. 89). Затем при помощи линий связи надо отыскать проекции точки, которые должны лежать на проекциях грани.

Линию связи сначала проводят к той проекции, на которой грань изображается в виде отрезка прямой.

Рис. 93. Построение проекций точки, лежащей на поверхности предмета

На рисунке 93 проекции грани, содержащие проекции точки А, выделены цветом. Точка A задана фронтальной проекцией а’. Горизонтальная проекция а этой точки должна лежать на горизонтальной проекции грани. Для ее нахождения проводят вертикальную линию связи из точки а’.

Чтобы найти профильную проекцию, нужно из точки а’ провести горизонтальную линию связи. В месте ее пересечения с отрезком прямой — проекцией грани лежит точка а».

Построение проекций точки В, изданной горизонтальной проекцией b, также показано линиями связи со стрелками.

1. На рисунке 94, а, б даны чертежи в системе прямоугольных проекций и наглядные изображения предметов. На видах буквами обозначены проекции вершин. Перечертите или перенесите на кальку заданные изображения. Обозначьте буквами остальные проекции вершин. Найдите эти вершины на наглядных изображениях и обозначьте их буквами.

Рис. 94. Задания для упражнений

2. Перечертите или перенесите на кальку заданные изображения (рис. 95) и постройте недостающие проекции точек, заданных на ребрах предмета. Выделите цветом проекции ребер (для каждого ребра свой цвет), содержащих точки. Нанесите точки на аксонометрической проекции и выделите теми же цветами ребра, на которых лежат точки.

Рис. 95. Задание для упражнений

3. Перечертите или перенесите на кальку рисунок 96. Постройте недостающие проекции точек, заданных на видимых поверхностях предмета. Выделите цветом проекции поверхностей, на которых лежат точки (для каждой поверхности свой цвет). Выделите поверхности предмета на наглядном изображении теми же цветами, что и на чертеже, и нанесите точки.

Рис. 96. Задание для упражнений

4. Перечертите или перенесите на кальку рисунок 97. Постройте недостающие проекции точек и обозначьте их буквами. Выделите цветом, как и в предыдущем задании, проекции поверхностей, на которых лежат эти точки.

Рис. 97. Задание для упражнений

Источник

Презентация по черчению на тему » Проекции вершин, ребер и граней предмета.» (7,9 класс)

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Тема урока: Проекции вершин, ребер и граней предмета. Презентация к уроку черчения Выполнила: Марченко Ирина Анатольевна, учитель черчения г. Таштагол, МБОУ ООШ№10, Кемеровская область

Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребер, граней и кривых поверхностей. Грань – это плоский многоугольник, ограничивающий поверхность многогранника. Ребро – это сторона грани. Вершина – это точка схода трех и более ребер. Кривая поверхность – это совокупность всех положений некоторой линии движущейся в пространстве.

а – видимая вершина; (b) – невидимая вершина Проекция вершины на плоскость – есть всегда точка (независимо от расположения). Проекция ребра на плоскость – зависит от его расположения. Проекция грани на плоскость – зависит от его расположения. А В а b Построения проекций вершин ребер и граней предмета. а / (b) / b а

Рефлексия Что нового вы узнали сегодня на уроке? В чём испытывали затруднения? Что понравилось на уроке?

Выполните три вида данной детали; На видах проставьте: проекции вершин А, В проекцию ребра АВ ДОМАШНЕЕ ЗАДАНИЕ: Прочитать §12 стр. 69-79 Выполнить чертеж в тетради по алгоритму. Образец выполнения работы см. на следующем слайде. B A

На рис 93.в учебнике даны точки А и В. А вам надо построить- А) три вида данной детали; Б) указать на трех видах данное ребро АВ, как показано на данном рисунке Образец выполнения данной работы смотри на следующем слайде

за внимание и работу! Спасибо

Номер материала: ДБ-1231199

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Мишустин поручил проводить международную олимпиаду по философии

Время чтения: 0 минут

СК предложил обучать педагогов выявлять деструктивное поведение учащихся

Время чтения: 1 минута

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

В Минпросвещения предложили приравнять нападения на школы к терактам

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

Минпросвещения разработало проект новых правил русского языка

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Урок по черчению на тему «Проекции вершин, ребер, граней предмета».

Ищем педагогов в команду «Инфоурок»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 2»

«Проекции вершин, граней и ребер предмета.»

учитель ИЗО и черчения

г. Ивантеевка. Московской области.

Тема: Проекции вершин, граней и ребер предмета.

Методы: Рассказ, объяснение, беседа, демонстрация, карточки – задания, упражнения, опорный конспект.

Оборудование: Компьютер, диапроектор, экран, чертёжные инструменты, тетрадь.

Тип урока: Комбинированный.

Словарная работа: Грань, ребро, вершина, кривая поверхность, конкурирующие точки.

1 Орг. момент – 1- 2 мин.

2. Новый материал – 15 мин

4. Заключительная часть урока – 2 – 3 мин.

Новый материал.
Объяснение сопровождается иллюстрациями на экране.
Сегодня мы поговорим о том, что на чертеже обозначают линии и точки.

(Демонстрация рис. на экране.)

Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребер, граней и кривых поверхностей.

— Начнем с граней. Что такое грань? Почему геометрические тела называются многогранниками? ( Грань – это плоский многоугольник, ограничивающий поверхность многогранника. )

-Что такое ребро? (Это сторона грани. )

— Что такое вершина? (Это точка схода трех и более ребер.)

— Как вы понимаете кривая поверхность? (Например, округлая или сферическая поверхность: цилиндр, конус)

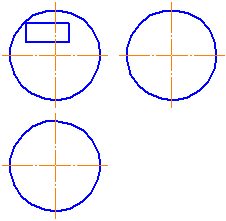
А теперь давайте закрепим полученные знания. Посмотрите на экран. Дано изображение детали. Вам необходимо выполнить упражнение в тетради.

Сосчитайте, сколько вершин имеет изображенный предмет. Обозначьте вершины цифрами.

Сколько ребер и граней у предмета?

Сосчитайте сколько у предмета ребер и граней, параллельных горизонтальной плоскости проекций.

Сколько ребер и граней, перпендикулярных горизонтальной плоскости проекций.

Заштрихуйте цветными карандашами на всех проекциях (каждая грань свой цвет) грани таким же способом (наклон штриха), что и штриховка на наглядных изображениях. Если грань проецируется на какой либо вид как линия, обведите ее нужным цветом.

(После решения задач, можно выборочно проверить тетради или на каждое задание вызывать учащихся к доске.)

Теперь, когда вы решили эти задачи вы наверняка заметили, что изображение любого предмета сводится к изображению его вершин, ребер, граней и кривых поверхностей.

Давайте более подробно рассмотрим этот процесс на примере построения прямоугольных проекций предмета. Посмотрите на экран.

Вы видите предмет, расположенный в трехгранном углу так, что бы его грани были параллельны плоскостям проекций, тогда они проецируются без искажений. Проведем через вершины предмета проецирующие лучи, перпендикулярные плоскости проекций. Отметим точки пересечения их с плоскостями. Эти точки будут вершинами на проекциях.

— Посмотрим на все три полученные вида. Как на главном виде проецируются вершины? ( В точки)

Проекции вершины А обозначаются точками: а’ a ’’ a соответственно.

-Посмотрите. Во что будет проецироваться ребро В D на фронтальную плоскость?

— А на профильную плоскость? (В точку)

Итак, когда ребро проецируется в отрезок, а когда в точку? (В отрезок- когда ребро параллельно плоскости, в точку- когда перпендикулярно.)

— Посмотрите теперь на наклонное ребро. Как оно проецируется на горизонтальную плоскость? Будет ли его длина равна его проекции? (Нет, проекция будет короче)

— А теперь подумайте и скажите, во что могут проецироваться грани? (Геометрическую фигуру или отрезок)

— От чего это зависит? Когда грань проецируется с искажением? (Когда она не параллельна плоскости проекций)

Строя чертеж, надо четко представлять, как изобразятся на нем каждая вершина, ребро и грань предмета.

Давайте закрепим знания.

На рисунке дан чертеж в системе прямоугольных проекций и наглядное изображение. На видах буквами обозначены проекции некоторых вершин. Обозначьте буквами остальные проекции вершин. Найдите эти вершины на наглядном изображении и тоже обозначьте их буквами.

Заключительная часть
Подведение итога.
Что вам понравилось на сегодняшнем уроке?
Что вас не устраивало на этом уроке (темп, объём и т. п. )?
Трудная – ли была работа на сегодняшнем уроке?
Добились ли вы поставленных целей?

Что вы сегодня на уроке узнали? (здесь возможно стоит задать вопросы, смотря по времени)

В каком случае грань (часть плоскости) проецируется в отрезок прямой?

В каком случае она спроецируется в истинную величину?

Что такое конкурирующие точки?

Как обозначаются не видимые точки?

Отметить лучших уч – ся. Отметить общие ошибки допускаемые во время работы.

Источник

Вершина (геометрия)

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.

В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.

Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.

Источник

Лекция 7. Поверхности

7.1. Поверхности. Образование и задание поверхности на чертеже

Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.

Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.

Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

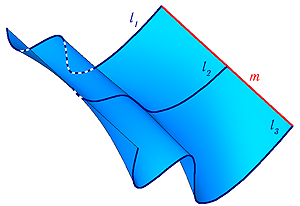
Поверхность можно рассматривать, как совокупность последовательных положений l₁,l₂… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).

Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.

Рисунок 7.1 — Кинематическая поверхность

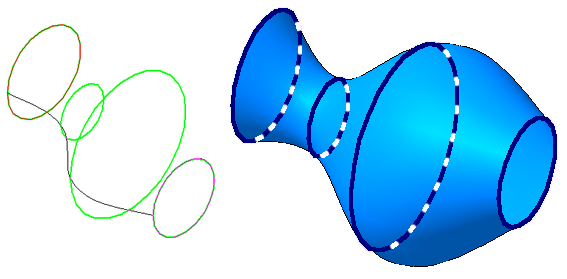
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).

Рисунок 7.2 — Циклическая поверхность

Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:

Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).

Для графического изображения поверхности на чертеже используется её каркас.

Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.

Различают две части определителя: геометрическую и алгоритмическую.

Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.

Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.

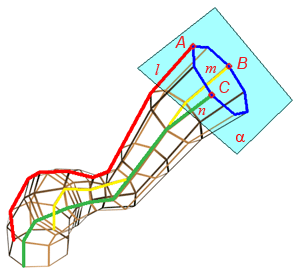
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:

Рисунок 7.3 –Образование циклической поверхности

7.2. Поверхности вращения

Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).

Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.

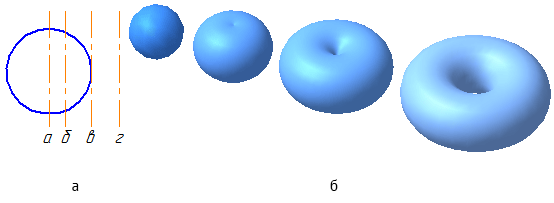
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.

Рисунок 7.4 – Образование поверхностей вращения

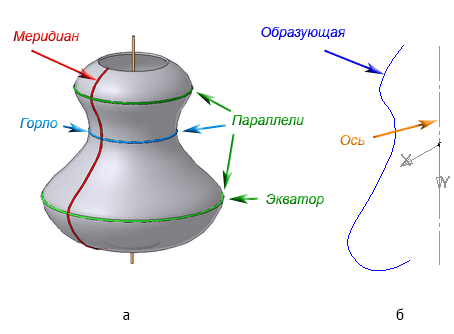
Рисунок 7.5 – Элементы поверхности вращения

Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).

7.3. Цилиндрическая поверхность

Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).

Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.

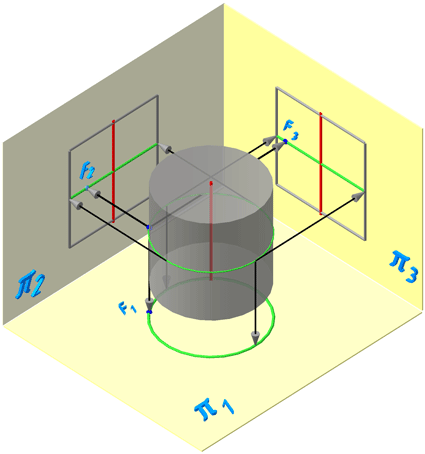
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.

Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).

Рисунок 7.6 – Проецирование цилиндра на плоскости проекций

Горизонтальная и профильная проекции точки F будут видимы.

При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π₁ сплошной зелёной линией – на плоскости проекции π₂ видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π₃.

Пусть точка А на π₂ видима (Рисунок 7.7). Тогда на π₁ она будет видима, а на π₃ невидима.

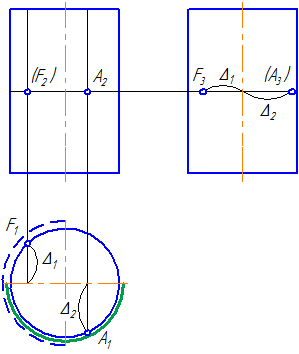
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек

7.4. Пересечение прямой с поверхностью прямого кругового цилиндра

Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.

Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.

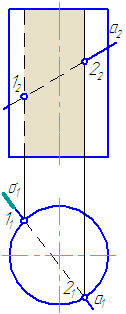
Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра

Упражнение

Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π₁ и прямая а общего положения (Рисунок 7.8).

Построить точки пересечения прямой а с поверхностью цилиндра.

Для построения точек пересечения прямой с поверхностью цилиндра необходимо:

Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.

Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π₂ будет ещё невидим участок прямой от точки 1 до левой крайней образующей.

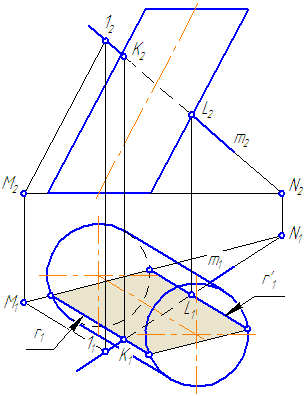
7.5. Пересечение прямой с поверхностью наклонного цилиндра

Упражнение

Заданы : наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π₁ и прямая mобщего положения (Рисунок 7.9).

Построить точки пересечения прямой mс поверхностью цилиндра.
Решение :

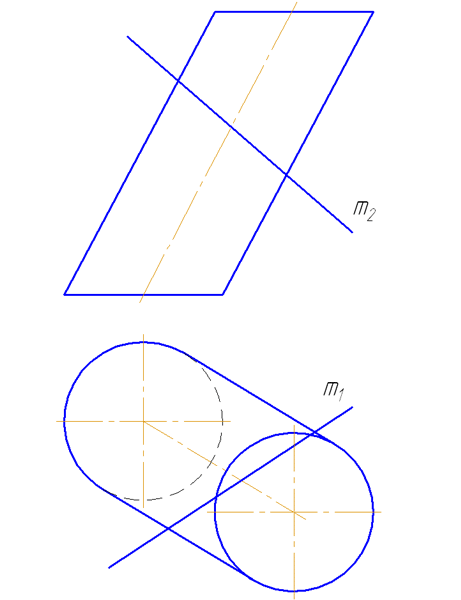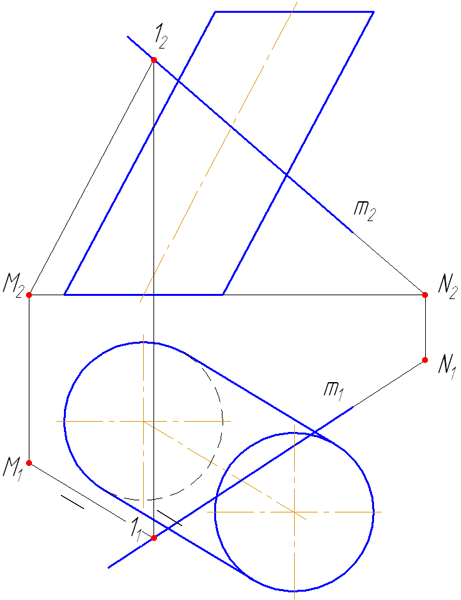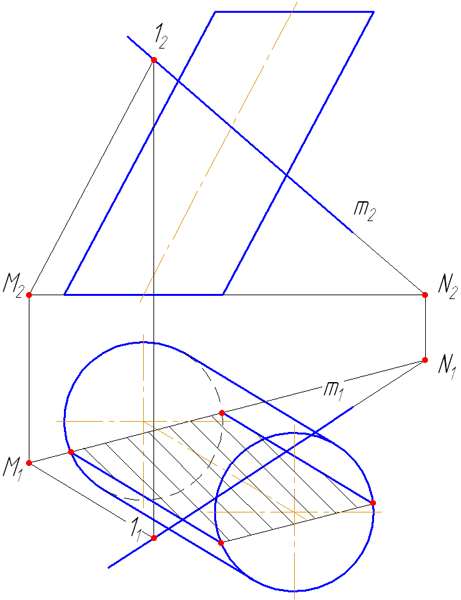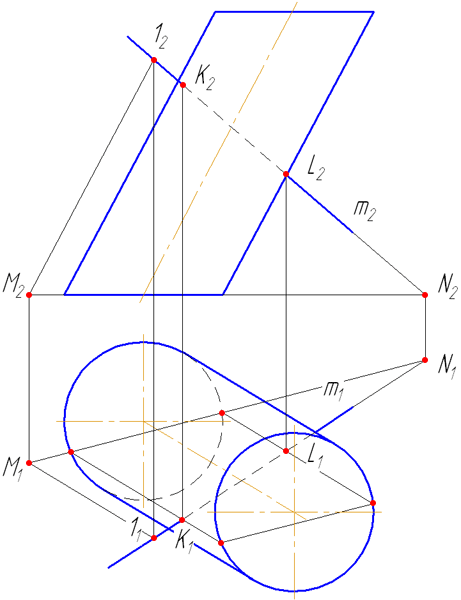
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:

Рисунок 7.9 – Пересечение прямой с наклонным цилиндром

На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

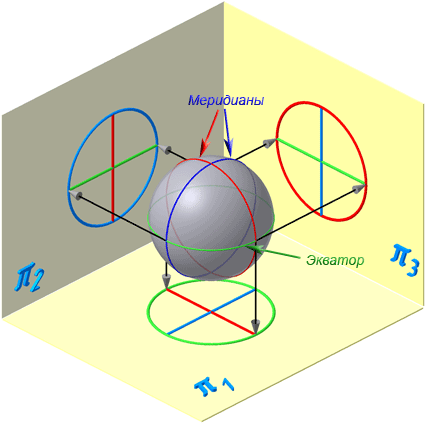
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

Рисунок 7.10 – Проецирование сферической поверхности

Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

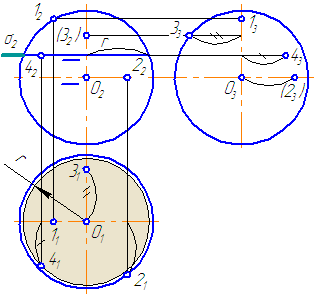
Упражнение

Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.

Необходимо построить горизонтальные и профильные проекции заданных точек.

7.7. Пересечение прямой с поверхностью сферы

Упражнение

Заданы: сфера и прямая общего положения АВ.

Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).

Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:

Рисунок 7.12 – Пересечение прямой с поверхностью сферы

7.8. Коническая поверхность

Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).

Рисунок 7.13 – Принадлежность точки конической поверхности

Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).

7.9. Пересечение прямой с поверхностью конуса

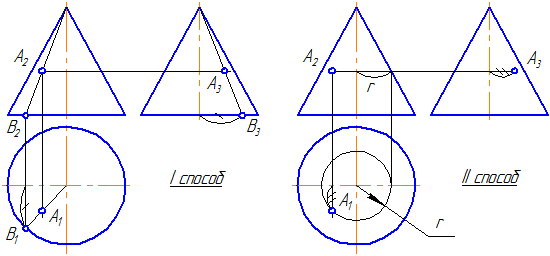
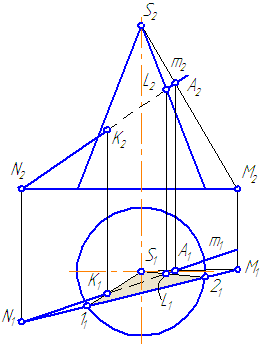
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.

Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).

Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса

На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.

7.10. Пересечение цилиндра плоскостью

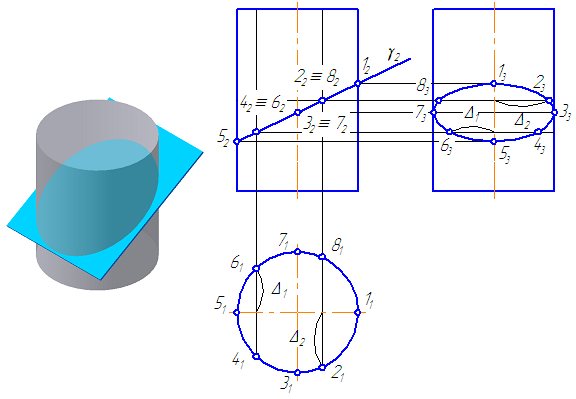
Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).

Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):

Рисунок 7.15 – пересечение цилиндра плоскостью

7.11. Пересечение сферы плоскостью

Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).

7.12. Пересечение конуса плоскостью

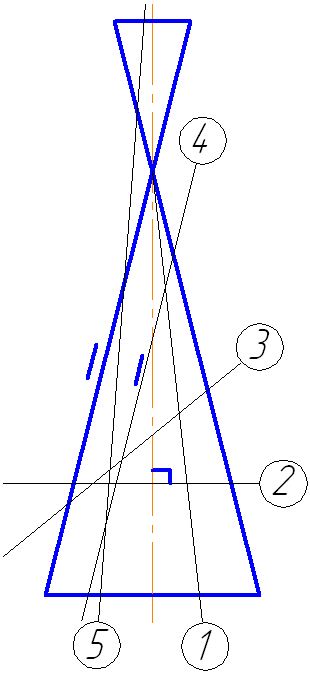
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

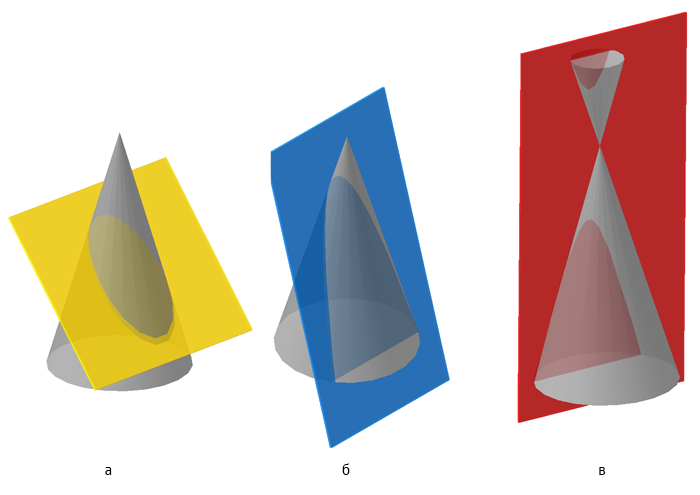
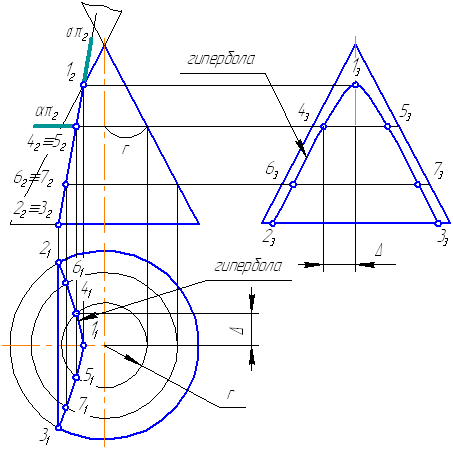
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

7.13. Задачи для самостоятельной работы

1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).

Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).

Рисунок 7.21

Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).

Рисунок 7.23

Источник