что такое вектор пойнтинга
Национальная библиотека им. Н. Э. Баумана
Bauman National Library
Персональные инструменты
Вектор Умова – Пойнтинга
Вектор Умова – Пойнтинга (так же Вектор Пойнтинга) – вектор плотности потока электромагнитной энергии, определяющий количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
Содержание
Общие положения
Вектор плотности потока электромагнитной энергии называется вектором Умова–Пойнтинга:
Векторы Умова–Пойнтинга зависят от пространства и времени, так как от них зависят модули векторов напряженности электрического и магнитного полей. Поэтому часто пользуются параметром, называемым интенсивностью – модуль среднего значения вектора Умова–Пойнтинга:
Интенсивность пропорциональна квадрату амплитуды:
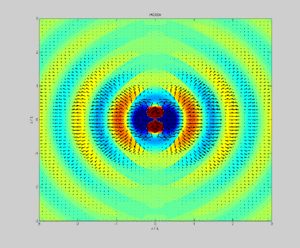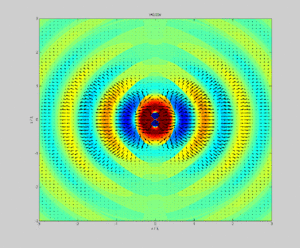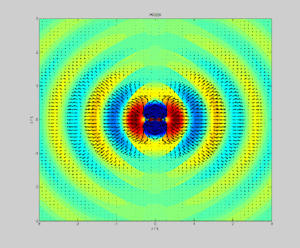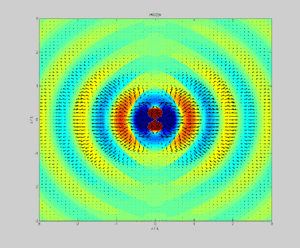
Зависимость интенсивности излучения от направления называют диаграммой направленности. Такая диаграмма для линейного излучателя показана на рис.3.
Как доказал Герц, диполь сильнее всего излучает в направлении перпендикулярном по отношению к собственному направлению.
Связь вектора Умова – Пойнтинга с импульсом электромагнитного поля
Вектор называется вектором Пойнтинга (вектором плотности потока электромагнитной энергии) и определяет количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Интеграл вектора Пойнтинга по сечению распространяющейся волны определяет её мощность. Важно отметить, что, как впервые указал Хевисайд, физический смысл потока энергии имеет только безвихревая часть вектора Пойнтинга. Вихревая часть, дивергенция которой равна нулю, не связана с переносом энергии. Заметим, чтоХевисайд получил выражение для закона сохранения независимо от Пойнтинга. В русскоязычной литературе вектор Пойнтинга часто называется также «вектором Умова — Пойнтинга».
Это уравнение показывает, что при отсутствии внутренних потерь изменение энергии электромагнитного поля в объёме происходит только за счёт мощности электромагнитного излучения, переносимого через границу этого объёма.
где интегрирование производится по всему пространству. Электромагнитная волна, поглощаясь или отражаясь от некоторой поверхности, передаёт ей часть своего импульса, что проявляется в форме светового давления. Экспериментально этот эффект впервые наблюдался П. Н. Лебедевым в 1899 году.
Замечания о векторе Умова – Пойнтинга
Обычно утверждается, что вектор Пойнтинга равен потоку электромагнитной энергии. Но это утверждение не всегда правильно. Например, если в пространстве имеется одновременно постоянное электрическое и постоянное магнитное поле, то вектор Пойнтинга может быть отличен от нуля, хотя в соответствующих точках поток энергии может отсутствовать.
Такие оговорки иногда делаются в современных учебниках, но не дается общего правила, позволяющего определить однозначную связь между вектором Пойнтинга и потоком энергии. Хевисайд дал правило, которое заключается в следующем:
СОДЕРЖАНИЕ
Определение
В оригинальной статье Пойнтинга и во многих учебниках вектор Пойнтинга определяется как
где жирные буквы обозначают векторы, а
В «микроскопической» версии уравнений Максвелла это определение должно быть заменено определением в терминах электрического поля E и плотности магнитного потока B (описанного далее в статье).
Также возможно объединить поле электрического смещения D с плотностью магнитного потока B, чтобы получить форму Минковского вектора Пойнтинга, или использовать D и H, чтобы построить еще одну версию. Выбор был спорным: Pfeifer et al. обобщить и в определенной степени разрешить многовековой спор между сторонниками форм Авраама и Минковского (см. противоречие Абрахама и Минковского ).
Интерпретация
Вектор Пойнтинга фигурирует в теореме Пойнтинга (вывод см. В этой статье), законе сохранения энергии:
где J F представляет собой плотность тока из свободных зарядов и у является плотность электромагнитной энергии для линейных, недиспергирующих материалов, дается
Для линейных, недисперсных и изотропных (для простоты) материалов определяющие соотношения можно записать в виде
В принципе, это ограничивает теорему Пойнтинга в такой форме полями в вакууме и недисперсными линейными материалами. Обобщение на дисперсные материалы возможно при определенных обстоятельствах за счет дополнительных условий.
Одним из следствий формулы Пойнтинга является то, что для того, чтобы электромагнитное поле работало, должны присутствовать как магнитное, так и электрическое поля. Одно только магнитное поле и одно электрическое поле не могут сделать никакой работы.
Формулировка в терминах микроскопических полей
Фактически это общее выражение вектора Пойнтинга. Соответствующая форма теоремы Пойнтинга такова:
Усредненный по времени вектор Пойнтинга
Вышеупомянутая форма вектора Пойнтинга представляет мгновенный поток энергии, обусловленный мгновенными электрическими и магнитными полями. Чаще всего проблемы в электромагнетизме решаются с помощью синусоидально изменяющихся полей на заданной частоте. Затем результаты можно применять в более общем плане, например, представляя некогерентное излучение как суперпозицию таких волн на разных частотах и с флуктуирующими амплитудами.
Эквивалентность Re ( S m ) среднему по времени мгновенного вектора Пойнтинга S можно показать следующим образом.
Среднее значение мгновенного вектора Пойнтинга S с течением времени определяется как:
Согласно некоторым соглашениям коэффициент 1/2 в приведенном выше определении может быть опущен. Умножение на 1/2 требуется для правильного описания потока мощности, поскольку величины E m и H m относятся к пиковым полям осциллирующих величин. Если, скорее, поля описываются в терминах их среднеквадратичных (среднеквадратичных) значений (каждое из которых меньше на коэффициент ), то правильный средний поток мощности получается без умножения на 1/2. 2 / 2 <\ displaystyle <\ sqrt <2>> / 2>
Примеры и приложения
Коаксиальный кабель
Резистивное рассеивание
Если проводник имеет значительное сопротивление, то вблизи поверхности этого проводника вектор Пойнтинга будет наклонен к проводнику и столкнется с ним. Как только вектор Пойнтинга входит в проводник, он изгибается в направлении, почти перпендикулярном поверхности. Это следствие закона Снеллиуса и очень низкой скорости света внутри проводника. Можно дать определение и вычисление скорости света в проводнике. Внутри проводника вектор Пойнтинга представляет поток энергии из электромагнитного поля в провод, вызывая резистивный джоулев нагрев в проводе. Для вывода, который начинается с закона Снеллиуса, см. Reitz, стр. 454.
Плоские волны
В распространяющейся синусоидальной линейно поляризованной электромагнитной плоской волне с фиксированной частотой вектор Пойнтинга всегда указывает в направлении распространения, колеблясь по величине. Усредненная по времени величина вектора Пойнтинга находится, как указано выше, равной:
Радиационное давление
Статические поля
Добавление ротора векторного поля
Вектор Пойнтинга
Из Википедии — свободной энциклопедии
Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
где E и H — векторы напряжённости электрического и магнитного полей соответственно.
В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии [2] :
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи.
Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.
Вектор Пойнтинга
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:


где E и H — векторы напряжённости электрического и магнитного полей соответственно.
В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии [1] :


где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи.
Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.
Вектор Пойнтинга и импульс электромагнитного поля
В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, делённым на квадрат скорости света:

В этом соотношении проявляется материальность электромагнитного поля.
Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объёму.
История
В 1884 году [3] идеи Умова были разработаны Д. Г. Пойнтингом применительно к электромагнитной энергии. Потому вектор плотности потока электромагнитной энергии называется вектором Пойнтинга.
Источники
Полезное
Смотреть что такое «Вектор Пойнтинга» в других словарях:
вектор Пойнтинга — Вектор, поток которого сквозь некоторую поверхность, представляющий собой мгновенную электромагнитную мощность, передаваемую сквозь эту поверхность, равен векторному произведению напряженности электрического поля и напряженности магнитного поля.… … Справочник технического переводчика
вектор Пойнтинга — 16 вектор Пойнтинга Вектор, поток которого сквозь некоторую поверхность, представляющий собой мгновенную электромагнитную мощность, передаваемую сквозь эту поверхность, равен векторному произведению напряженности электрического поля и… … Словарь-справочник терминов нормативно-технической документации
вектор Пойнтинга — Pointingo vektorius statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis, išreiškiamas vektorine elektrinio ir magnetinio laukų stiprių sandauga: S = E · H; čia S – Pointingo vektorius, E ir H – elektrinio ir magnetinio… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Вектор Пойнтинга — Вектор, поток которого сквозь некоторую поверхность, представляющий собой мгновенную электромагнитную мощность, передаваемую сквозь эту поверхность, равен векторному произведению напряженности электрического поля и напряженности магнитного поля … Официальная терминология
вектор Пойнтинга — Вектор, характеризующий распространение энергии электромагнитной волны, равный векторному произведению напряженностей электрического и магнитного полей … Политехнический терминологический толковый словарь
вектор Пойнтинга (в оптике) — вектор Пойнтинга ( ) Векторная величина, направление которой совпадает с направлением распространения энергии излучения, а абсолютное значение равно отношению мощности излучения, проходящего сквозь перпендикулярную к направлению вектора… … Справочник технического переводчика
Вектор Умова-Пойнтинга — Вектор Пойнтинга (в российской научной традиции вектор Умова Пойнтинга) это вектор плотности потока энергии электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов: (в системе СГС), (в системе СИ),… … Википедия
Пойнтинга вектор — Вектор Пойнтинга (в российской научной традиции вектор Умова Пойнтинга) это вектор плотности потока энергии электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов: (в системе СГС), (в системе СИ),… … Википедия
Вектор Умова — Вектор Пойнтинга (в российской научной традиции вектор Умова Пойнтинга) это вектор плотности потока энергии электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов: (в системе СГС), (в системе СИ),… … Википедия
ПОЙНТИНГА ТЕОРЕМА — теорема, описывающаязакон сохранения энергии эл. магн. поля. Теорема была доказана в 1884 Дж … Физическая энциклопедия
Вектор Пойнтинга стоячей волны
Модуль вектора Пойнтинга
Стоячие волны
Стоячими волнами называют волны, которые образуются при наложении двух бегущих волн, которые распространяются друг навстречу другу и имеют одинаковые амплитуды и частоты.
Если мы имеем дело с двумя плоскими волнами, распространяющимися навстречу друг другу по оси X без затухания, то уравнение стоячей волны можно записать как:
К особенностям стоячих волн в сравнении с бегущими волнами, относят то, что:
Примеры задач на вектор Пойнтинга стоячей волны
Задание. Вычислите вектор Пойнтинга для стоячей электромагнитной волны.
Колебания полей в стоячей электромагнитной волне можно представить при помощи формул:
Решение.Прежде всего, введем обозначения:
Тогда заданную систему уравнений (1.1) можно переписать как:
Задание. Чему равна средняя величина по времени вектора Пойнтинга в стоячей электромагнитной волне?
Решение. Для ответа на поставленный вопрос воспользуемся ответом предыдущего примера:
Формула (2.2) означает, что в стояче волне нет течения энергии. Периодическое изменение знака вектора Пойнтинга показывает, что направление движения энергии периодически изменяется. Энергия совершает колебания между пучностями электрического и пучностями магнитного полей.