что такое вектор нормали
Нормальный вектор плоскости, координаты нормального вектора плоскости
Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.
Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
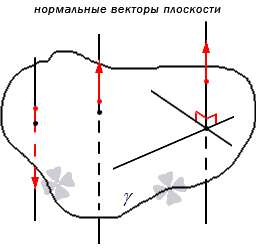
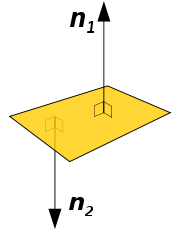
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Вектор нормали
В дифференциальной геометрии, нормаль — это прямая, ортогональная (перпендикулярная) касательной прямой к некоторой кривой или касательной плоскости к некоторой поверхности. Также говорят о нормальном направлении.
Вектор нормали к поверхности в данной точке — это единичный вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Если на поверхности можно задать непрерывное поле нормальных векторов, то говорят, что это поле задает ориентацию поверхности (то есть выделяет одну из сторон). Если этого сделать нельзя, поверхность называется неориентируемой.
Смотреть что такое «Вектор нормали» в других словарях:
вектор нормали — normalės vektorius statusas T sritis fizika atitikmenys: angl. normal vector vok. Normalenvektor, m rus. вектор нормали, m pranc. vecteur de la normale, m; vecteur normal, m … Fizikos terminų žodynas
Вектор Дарбу — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Вектор Дарбу направляющий вектор мгновенной оси вращения, вокруг которой сопровождающий триэдр кривой L поворачивается при… … Википедия
Вектор электрической поляризации — Электродинамика сплошных сред Электродинамика сплошных сред … Википедия
Дарбу вектор — Вектор Дарбу направляющий вектор мгновенной оси вращения, вокруг которой сопровождающий триэдр кривой L поворачивается при равномерном движении точки M по кривой L. Вектор Дарбу лежит в спрямляющей плоскости кривой L и выражается через единичные… … Википедия
Градиент (вектор) — Градиент (от лат. gradiens, род. падеж gradientis шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой (см. Поля теория). Если величина выражается… … Большая советская энциклопедия
ДАРБУ ВЕКТОР — направляющий вектор d мгновенной оси вращения, вокруг к рой сопровождающий триэдр кривой Lповорачивается при равномерном движении точки Мпо кривой L. Д. в. лежит в спрямляющей плоскости кривой Lи выражается через единичные векторы главной нормали … Математическая энциклопедия
Гиперповерхность — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Гиперповерх … Википедия
Графический конвейер — Графический конвейер аппаратно программный комплекс визуализации трёхмерной графики. Содержание 1 Элементы трехмерной сцены 1.1 Аппаратные средства 1.2 Программные интерфейсы … Википедия
Векторное исчисление — математическая дисциплина, в которой изучают свойства операций над Векторами евклидова пространства. При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и… … Большая советская энциклопедия
Плоскость (геометрия) — У этого термина существуют и другие значения, см. Плоскость. Сюда перенаправляется запрос «Плоскостность». На эту тему нужна отдельная статья … Википедия
Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
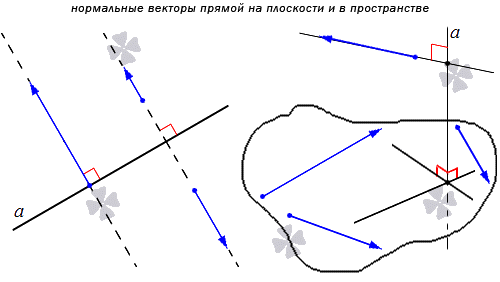
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
Для решения можно выбирать любой удобный способ.
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора 

Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
Нормаль
Вектор нормали к поверхности в данной точке — единичный вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Если на поверхности можно задать непрерывное поле нормальных векторов, то это поле задаёт ориентацию поверхности (то есть выделяет одну из сторон). Если этого сделать нельзя, поверхность называется неориентируемой.
Аналогично определяется вектор нормали к кривой в данной точке. Очевидно, что к кривой в данной точке можно приложить бесконечно много непараллельных векторов нормали (аналогично тому, как к поверхности можно приложить бесконечно много непараллельных касательных векторов). Среди них выбирают два, ортогональных друг к другу: вектор главной нормали и вектор бинормали.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.
В релятивистской физике координатами Риндлера называется важная и полезная координатная система, представляющая часть плоского пространства-времени, также называемого пространством Минковского. Координаты Риндлера были введены Вольфгангом Риндлером для описания пространства-времени равномерно ускоренного наблюдателя.
Три вектора (или большее число) называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).
Отношение инцидентности — это бинарное отношение между двумя различными типами объектов. Это включает понятия, которые можно выразить такими фразами как «точка лежит на прямой» или «прямая принадлежит плоскости». Наиболее существенное отношение инцидентности — между точкой P и прямой l, которое записывается как P I l. Если P I l, пара (P, l) называется флагом. В разговорном языке существует много выражений, описывающих отношение инцидентности (например, прямая проходит через точку, точка лежит на.