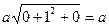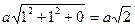что такое вектор бюргерса в краевых дислокациях
Вектор Бюргерса
Вектор Бю́ргерса (b) — количественная характеристика, описывающая искажения кристаллической решётки вокруг дислокации.
Важнейшие виды линейных дефектов — краевые и винтовые дислокации. Краевая дислокация представляет собой край «лишней» полуплоскости в решётке. Вокруг дислокаций решётка упруго искажена.
Величина и направление вектора не зависят от размеров контура Бюргерса и выбора точки начала контура, а полностью определяются видом дислокации. У краевой дислокации вектор Бюргерса равен межатомному расстоянию и перпендикулярен дислокационной линии, у винтовой дислокации — параллелен ей.
Полные дислокации легко перемещаются под действием напряжений в отличие от частичных дислокаций, у которых вектор Бюргерса меньше межатомного расстояния.
Скачок вектора Бюргерса в некоторой точке означает, что дислокация ветвится. Если точек ветвления нет, то вектор Бюргерса остаётся неизменным вдоль всей длины дислокации, поэтому дислокация не может начинаться или обрываться внутри кристалла.
Внутри кристалла дислокации связаны в единую объемную сетку; в каждом узле сетки соединены три дислокации и сумма их векторов Бюргерса равна нулю.
В кристаллах содержатся дислокации разных знаков, различающиеся ориентаций векторов Бюргерса. Дислокации одного знака, расположенные в одной плоскости, отталкиваются друг от друга, а противоположных знаков — притягиваются.
Примечания
Литература
Материаловедение: Учебник для высших технических учебных заведений. Б.Н. Арзамасов, И. И. Сидорин, Г. Ф. Косолапов и др.; Под общ. ред. Б. Н. Арзамасова. — М.: Машиностроение, 1986.— 384 с. С. 26.
Полезное
Смотреть что такое «Вектор Бюргерса» в других словарях:
вектор Бюргерса — Показывает величину и направление смещения атомов в той области кристалла, где произошел сдвиг кристаллич. решетки из за наличия в ней дислокации. [http://metaltrade.ru/abc/a.htm] Тематики металлургия в целом EN Burgers vector … Справочник технического переводчика
вектор Бюргерса — Burgerso vektorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dislokaciją apibūdinantis vektorius, t. y. Burgerso grandinės, apsupančios dislokacijos liniją, uždarantysis vektorius. atitikmenys: angl. Burgers vector vok. Burgers… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
вектор Бюргерса — Burgerso vektorius statusas T sritis fizika atitikmenys: angl. Burgers vector vok. Burgers Vektor, m rus. вектор Бюргерса, m pranc. vecteur de Burgers, m … Fizikos terminų žodynas
вектор Бюргерса — [Burgers vector] показывает величину и направление смещения атомов в той области кристалла, где произошел сдвиг кристаллической решетки из за наличия в ней дислокации. Смотри также: Вектор вектор элементарной трансляции вектор тождественной… … Энциклопедический словарь по металлургии
Бюргерса вектор — Вектор Бюргерса (b) количественная характеристика, описывающая искажения кристаллической решётки вокруг дислокации. Важнейшие виды линейных дефектов краевые и винтовые дислокации. Краевая дислокация представляет собой край «лишней» полуплоскости … Википедия
Вектор — Вектор многозначный термин; величина, характеризующаяся размером и направлением. В Викисловаре есть статья «вектор» … Википедия
Вектор (значения) — Вектор: Содержание 1 В биологии 2 В информатике 3 В математике 4 В физике … Википедия
вектор элементарной трансляции — [vector of elementary translation] Вектор тождественной трансляции, имеющий минимальную величину. Смотри также: Вектор вектор тождественной трансляции вектор Бюргерса … Энциклопедический словарь по металлургии
вектор напряжений — [stress vector] аΔS→0=limΔS→0 Δ→FΔS где Δ→F/ вектор силы, действующий от отброшенной части тела на выделенном элементе сечения ΔS. Компоненты вектора напряжения, лежащие в плоскости сечения … Энциклопедический словарь по металлургии
вектор тождественной трансляции — [vector of identical translation] показывает величину и направление возможного переноса кристаллической решетки, при котором ее конечное положение нельзя отличить от начального. Смотри также: Вектор вектор элементарной трансляции вектор Бюргерса… … Энциклопедический словарь по металлургии
Вектор Бюргерса
Вектор Бюргерса является мерой искаженности кристаллической решетки, обусловленной присутствием в ней дислокации. Он определяет энергию дислокации, действующие на дислокацию силы, величину связанного с дислокацией сдвига, влияет на подвижность дислокации. Следовательно, вектор Бюргерса — главная количественная характеристика дислокации.
Если дислокация вводится в кристалл чистым сдвигом, то вектор сдвига и является вектором Бюргерса. Вектор сдвига определяет величину и направление смещений атомов в той области, где сдвиг уже произошел, т. е. определяет степень искаженности решетки, связанную с присутствием дислокации, введенной в кристалл путем сдвига. Однако дислокация далеко не всегда вызывается сдвигом. Кроме того, не все типы дислокаций можно определить через вектор сдвига. Поэтому более общим является определение вектора Бюргерса не как вектора сдвига, а как меры искаженности кристаллической решетки.
Чтобы оценить степень искаженности решетки, вызванной дислокацией, следует сравнить несовершенный кристалл, содержащий дислокацию, с совершенным кристаллом. Для этого строят так называемый контур Бюргерса. Контуром Бюргерса называется замкнутый контур произвольной формы, построенный в реальном кристалле путем последовательного обхода дефекта от атома к атому в совершенной области кристалла.
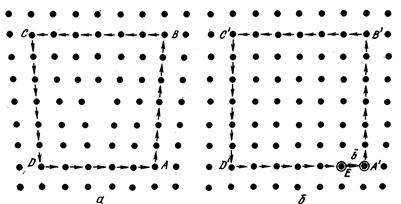
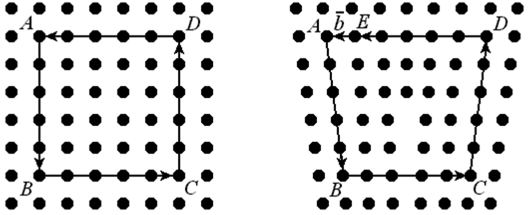
На рис.10.4, а показано построение контура Бюргерса вокруг краевой дислокации. За исходную точку принят атом А. Строя контур, пойдем вверх в совершенной области от атома к атому. Пройдя вверх шесть межатомных расстояний, в точке В остановимся и пойдем налево; через шесть межатомных расстояний достигнем точки С и пойдем вниз (мы могли бы по горизонтали справа налево пройти не шесть, а пять, семь или восемь межатомных расстояний). Вниз от точки С, отсчитав шесть межатомных расстояний, попадаем в точку D, находящуюся на одном уровне с точкой А.
Рис. 10.4. Контур Бюргерса вокруг краевой дислокации (а) и эквивалентный контур в совершенном кристалле (б): b— вектор Бюргерса
Чтобы замкнуть контур на отрезке DA, необходимо пройти не произвольное, а строго определенное число межатомных расстояний—ровно пять. Замкнутая линия ABCD, соединяющая атомы совершенной области решетки и охватывающая краевую дислокацию, является контуром Бюргерса.
Проведем соответствующий контур в совершенном кристалле, т. е. кристалле без дислокации (рис. 10.4, б). Выберем произвольно в качестве исходной точки атом А’ и пройдем вверх от него шесть межатомных расстояний (до точки В’), затем влево—шесть (до точки С’), вниз—шесть (до точки D’) и вправо—пять межатомных расстояний, т. е. повторим число и направление «шагов», сделанных при построении контура ABCD. Пройдя пять межатомных расстояний вправо от точки D’, мы попадаем в точку Е, а не в исходную точку А’: контур получается незамкнутым. Вектор b, проведенный из точки Е в точку А’ и замыкающий контур, является вектором Бюргерса. Невязка (разомкнутость) контура A’B’C’D’E в совершенном кристалле обусловлена тем, что в кристалле с дислокацией из-за экстраплоскости на стороне ВС, находящейся в верхней половине кристалла, на один атом больше, чем на стороне DA, находящейся в нижней половине кристалла.
Вокруг дислокации атомы в совершенной области, где проходит контур Бюргерса ABCD, несколько смещены по сравнению с расположением их в совершенном кристалле без дислокации. Сумма всех упругих смещении, накопившаяся при обходе по контуру Бюргерса ABCD, и проявляется в виде невязки, когда соответствующий контур строят в совершенном кристалле. Поэтому вектор Бюргерса, замыкающий в совершенном кристалле контур Бюргерса, является мерой той искаженности решетки в несовершенном кристалле, которая вызвана дислокацией.
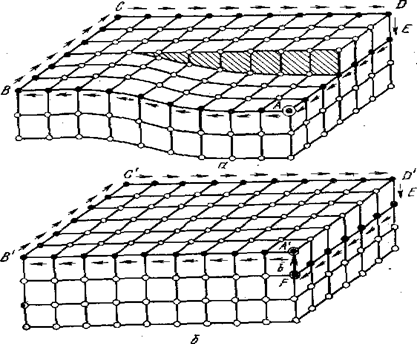
Рис. 10.5. Контур Бюргерса вокруг винтовой дислокации (а) и эквивалентный контур в совершенном кристалле (6)
Величина вектора Бюргерса не зависит от того, насколько контур Бюргерса удален от дислокации. Чем дальше от дислокации мы располагаем этот контур, тем меньше упругие смещения атомов в совершенной области, но тем длиннее контур, и сумма всех упругих смещений, накопившаяся при его обходе, неизменна.
Рис. 10.5 демонстрирует построение контура и вектора Бюргерса для случая винтовой дислокации. Контур Бюргерса можно, например, построить от исходной точки А (рис 10.5,а). Пройдем от нее влево девять межатомных расстояний до точки В, шесть — до точки С и вправо девять — до точки D. Чтобы попасть на уровень исходной точки А, спустимся от точки D по вертикали вниз до точки Е на одно межатомное расстояние и пройдем шесть межатомных расстояний от Е до А.
Для проведения соответствующего контура в совершенном кристалле (рис. 10.5,б) сделаем девять «шагов» от исходной точки А’ до В’, затем шесть — до С’, девять — до D’, один шаг вниз по вертикали от D’ до Е’ и шесть шагов — на горизонтальном уровне в сторону исходной точки. При этом мы попадаем не в исходную точку А’, а в точку F. Невязку контура ликвидируем, замыкая его вектором Бюргерса b (соединяя точки F и А’). Этот вектор на рис. 5,б характеризует степень искаженности решетки, вызванной винтовой дислокацией в кристалле на рис. 10.5, а. Весьма удобно, что искаженность решетки несовершенного кристалла выражается через период решетки идеального кристалла, т. е. через константу.
Легко увидеть, что векторы Бюргерса, полученные на рис. 10.1 и 10.2, являются векторами сдвига.
Направление вектора Бюргерса зависит от направления обхода по контуру Бюргерса. Следовательно, в понятии вектора Бюргерса содержится неопределенность, соответствующая углу в 180 град. Но это не является серьезным недостатком, так как сущность указанной неопределенности сводится к тому, например, что пробег краевой дислокации через весь кристалл (рис.10.5) вызвал сдвиг верхней половины кристалла влево относительно нижней или, что то же самое, сдвиг нижней половины кристалла вправо относительно верхней половины.
Вектор Бюргерса характеризуется рядом особенностей:
1. Нормален к линии краевой дислокации и параллелен линии винтовой дислокации. Вдоль линии смешанной дислокации угол между ней и вектором Бюргерса в разных точках имеет разную величину (см. рис. 9.10.6).
2. У дефектов недислокационного типа равен нулю. Если построить контур Бюргерса вокруг любого точечного дефекта или линейного дефекта недислокационного типа (вокруг цепочки атомов или вакансий), то соответствующий контур в идеальном кристалле окажется замкнутым.
3. Одинаков вдоль всей линии дислокации, т.е. является инвариантом дислокации. Это следует, например, из того, что при смещении контура Бюргерса вдоль линии дислокации он все время будет оставаться эквивалентным исходному контуру (при условии, что он всеми своими точками не выходит из совершенной области решетки, т. е. не пересекает другие несовершенства). Кроме того, вектор сдвига, создающего, например, криволинейную смешанную дислокацию, имеет одну величину и одно направление для всего кристалла.
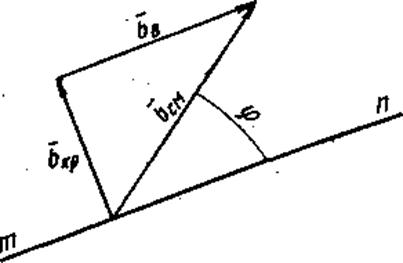
Вектор Бюргерса смешанной дислокации можно разложить на краевую и винтовую компоненты, которые зависят от угла φ между вектором Бюргерса и линией смешанной дислокации.
Из инвариантности вектора Бюргерса вытекает важное следствие: дислокация не может обрываться внутри кристалла. Допустив противное, продвинем контур Бюргерса за предполагаемую точку обрыва дислокации. Контур останется неизменным, так как все время находится в области с совершенной решеткой. Но если ему соответствует прежний вектор Бюргерса, отличный от нуля, это значит, что внутри контура Бюргерса все время присутствует дислокация, т. е. обрыв ее внутри кристалла невозможен. Дислокация может обрываться только на границе кристалла. Внутри кристалла дислокации могут образовывать замкнутые петли с одинаковым вектором Бюргерса вдоль всей петли или встречаться с другими дислокациями, образовывая узлы (точки встречи).
Рис. 10.6. Краевая и винтовая составляющие вектора Бюргерса смешанной дислокации
То, что дислокация не обрывается внутри кристалла, можно доказать, следующим весьма наглядным путем. Дислокация является границей зоны сдвига, которая должна быть замкнутой линией.
Вектор Бюргерса и линия дислокации однозначно определяют возможную плоскость (поверхность) скольжения.
Поскольку вектор Бюргерса — столь важная количественная характеристика дислокации, необходимо уметь обозначать его так, чтобы запись его отражала направление и величину вектора.
Если вектор b по трем координатным осям х, у и z имеет составляющие bх, bу и bz, то это записывается так: b = [bxbybz]
Величину вектора Бюргерса или, как часто говорят, его мощность легко определить:
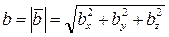
За направления осей х, у и z обычно принимают кристаллографические направления ребер элементарной ячейки данной решетки. В случае кубической решетки составляющие по осям Ьх, by и Ьг можно выразить через период элементарной ячейки а.
Этот период войдет в общий наибольший делитель па, где п — некоторое число. Тогда
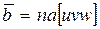
Здесь и, v и w — целые числа, a [uvw] является символом кристаллографического направления вектора Бюргерса. Мощность же

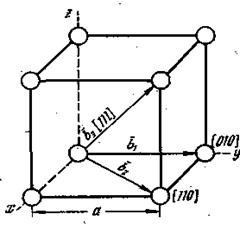 |
Рис. 10.7. Векторы Бюргерса в примитивной кубической решетке
Для вектора 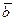
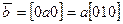
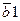
Для вектора 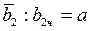
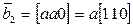
Для вектора 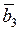
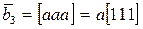
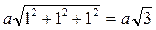
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Что такое вектор Бюргерса в краевых дислокациях
Билет 2
Что такое вектор Бюргерса в краевых дислокациях
Вектор Бюргерса (ВБ) является мерой искаженности кристалла, обусловленной присутствием в ней дислокации. Он определяет энергию дислокации, величину связанного с дислокацией сдвига, влияет на подвижность дислокации. Следовательно, вектор Бюргерса — главная количественная характеристика дислокации.
Если дислокация вводится в кристалл путем чистого сдвига, а мы выше так и делали, то вектор сдвига является вектором Бюргерса.
Однако дислокация далеко не всегда вызывается сдвигом и не все типы дислокаций можно определить через вектор сдвига. Поэтому более общим является определение вектора Бюргерса не как вектора сдвига, а как меры искаженности кристалла.
Чтобы определить степень искаженности кристалла, вызванную дислокацией, следует сравнить несовершенный кристалл, содержащий дислокацию, с совершенным кристаллом. Для этого используют построение так называемого контура Бюргерса (KБ).
Контуром Бюргерса называется замкнутый контур произвольной формы, построенный в реальном кристалле путем последовательного обхода дефекта от атома к атому в совершенной области кристалла.
Вектор Бюргерса замыкает в совершенном кристалле контур Бюргерса и является мерой искаженности кристалла, вызванной дислокацией. Величина ВБ не зависит от того, насколько КБ удален от дислокации. Чем дальше от дислокации мы располагаем этот контур, тем меньше упругие смещения атомов в совершенной области, но тем длиннее контур, и сумма всех упругих смещений, накопившаяся при его обходе, остается постоянной.
Контур и вектор Бюргерса
При рассмотрении теории дислокаций часто используют понятия контура Бюргерса и вектора Бюргерса.
Контур Бюргерса представляет собой замкнутый контур, проведенный в кристалле в области неискаженного материала и охватывающий линейный дефект решетки. На рис. 8.5 показано построение этого контура в совершенном кристалле, не имеющем дислокаций. За исходную точку принят атом А. двигаясь вниз на пять межатомных расстояний, в точке В повернем направо и пройдем такой же отрезок в пять шагов (до узла С), а затем поднимемся до узла D (вновь то же расстояние) и вернемся к исходному атому А. в результате такой процедуры получится замкнутый контур.
Рис. 8.5. Контур Бюргерса в совершенном кристалле (а), в кристалле, содержащем дислокацию (б)
Построим теперь аналогичный контур в кристалле, содержащем дислокацию (рис. 8.5 б). если полностью повторить предыдущий путь при движении от узла А через позиции B, C, D, то легко видеть, что контур окажется незамкнутым. Чтобы вернуться в исходный узел А, требуется совершить еще один шаг на величину межатомного расстояния. Иными словами, для замыкания контура нужен отрезок ЕА. Вектор b, проведенный из узла Е в узел А и замыкающий контур, называется вектором Бюргерса. Таким образом, дислокацию можно охарактеризовать не только как границу незавершенного сдвига, но и как одномерный дефект, для которого вектор Бюргерса отличен от нуля. Вектор Бюргерса показывает величину и направление сдвига, вызванного движением дислокации. Он считается важной количественной характеристикой дислокации, которая определяет энергию дислокации, является показателем упругих искажений решетки, создаваемых этим дефектом и мерой ее подвижности.
Можно также отметить, что вектор Бюргерса рассматривается и как трансляционный вектор, так как перенос на его величину и по его направлению переводит кристалл в положение самосовпадения – после завершения сдвига на величину вектора b прежняя конфигурация атомов в решетке полностью восстанавливается.
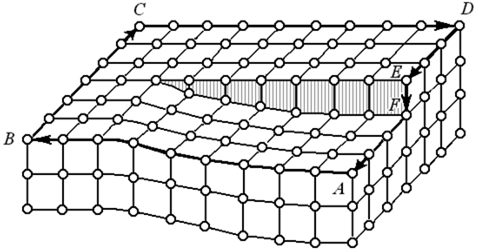
Построение контура и вектора Бюргерса для винтовой дислокации показано на рис. 8.6. За начало отсчета принят узел А. Построим контур путем последовательного перемещения по поверхности кристалла, имеющего винтовую дислокацию. В этом случае при достижении позиции Е необходимо будет сместиться вниз на одно межатомное расстояние (EF), чтобы иметь возможность вернуться в исходную точку А. При построении аналогичного контура в бездефектном кристалле дополнительного шага совершать не придется. Тем самым при обходе контура Бюргерса в кристалле, имеющем винтовую дислокацию, отрезок EF, параллельный линии l этой дислокации, будет отражать ее вектор Бюргерса.
Рис. 8.6. Контур Бюргерса вокруг винтовой дислокации
Поскольку любая дислокация является границей зоны сдвига, то она не может обрываться внутри кристалла. Дислокация в состоянии лишь выходить своими концами на поверхность, разветвляться на несколько дислокаций, образующих узел или формировать замкнутое кольцо, полностью расположенное в кристалле. Учитывая, что дислокационная линия в общем случае может иметь произвольную кривизну, то вводится понятие о смешанной дислокации, имеющей различную долю краевой и винтовой компонент. Таким образом, любую произвольную линию дислокации можно разделить на краевую и винтовую составляющие.
Вектор Бюргерса
Важнейшие виды линейных дефектов — краевые и винтовые дислокации. Краевая дислокация представляет собой край «лишней» полуплоскости в решётке. Вокруг дислокаций решётка упруго искажена.
Мерой искажения служит так называемый вектор Бюргерса. Он получается, если в реальном кристалле обойти контур, который был бы замкнутым в идеальном кристалле (например, в примитивном кристалле кубической сингонии это контур «n связей вверх, m связей вправо, n связей вниз, m связей влево»), заключив дислокацию «внутрь» контура. Как видно на рисунке, в реальном кристалле контур окажется незамкнутым. Вектор b, который нужен для замыкания контура, называется вектором Бюргерса.
Величина и направление вектора не зависят от размеров контура Бюргерса и выбора точки начала контура, а полностью определяются видом дислокации. У краевой дислокации вектор Бюргерса равен межатомному расстоянию и перпендикулярен дислокационной линии, у винтовой дислокации — параллелен ей.
Полные дислокации легко перемещаются под действием напряжений в отличие от частичных дислокаций, у которых вектор Бюргерса меньше межатомного расстояния.
Скачок вектора Бюргерса в некоторой точке означает, что дислокация ветвится.
Если точек ветвления нет, то вектор Бюргерса остаётся неизменным вдоль всей длины дислокации, поэтому дислокация не может начинаться или обрываться внутри кристалла.
Внутри кристалла дислокации связаны в единую объемную сетку; в каждом узле сетки соединены три дислокации и сумма их векторов Бюргерса равна нулю.
В кристаллах содержатся дислокации разных знаков, различающиеся ориентаций векторов Бюргерса. Дислокации одного знака, расположенные в одной плоскости, отталкиваются друг от друга, а противоположных знаков — притягиваются.
Связанные понятия
В релятивистской физике координатами Риндлера называется важная и полезная координатная система, представляющая часть плоского пространства-времени, также называемого пространством Минковского. Координаты Риндлера были введены Вольфгангом Риндлером для описания пространства-времени равномерно ускоренного наблюдателя.
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость.
Мультипо́ли (от лат. multum — много и греч. πόλος — полюс) — определённые конфигурации точечных источников (зарядов). Простейшими примерами мультиполя служат точечный заряд — мультиполь нулевого порядка; два противоположных по знаку заряда, равных по абсолютной величине — диполь, или мультиполь 1-го порядка; 4 одинаковых по абсолютной величине заряда, размещённых в вершинах параллелограмма, так что каждая его сторона соединяет заряды противоположного знака (или два одинаковых, но противоположно направленных.
Кристалл — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек, которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит.
В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны.