что такое сингулярное состояние
Что такое сингулярность? Точка сингулярности. Сингулярность черной дыры
Что такое сингулярность?
Общая трактовка термина
Разгадываем тайны гравитации
В астрофизике существует такое понятие, как скорость убегания. Оно используется для того, чтобы определить степень разгона, с которой определенный объект сможет сопротивляться гравитационным силам. К примеру, ракета с учетом ее массы должна двигаться со скоростью около 12 км/с, чтобы покинуть атмосферу Земли. Но если бы наша планета имела диаметр не 12 742 километра, а один сантиметр, то для преодоления поля притяжения нужно было бы двигаться со скоростью большей, чем скорость света. В таком случае Землю окружала бы не привычная нам сила тяготения, а гравитационная сингулярность. Конечно же, все это теория, так как если наша планета примет подобные размеры, она превратится в черную дыру. Но такой опыт дает возможность понять, каково значение гравитации во Вселенной. т чего зависит сила тяготения? Чем ближе атомы располагаются друг к другу, тем плотнее вещество. Если молекулы как-либо взаимодействуют между собой, то происходит процесс нагревания, следовательно, температура этого вещества повышается. В земных условиях такие процессы происходят в определенных рамках, потому мы давно изобрели формулы, позволяющие рассчитать поведение любого химического элемента. Все потому, что сила земного притяжения не дает частицам сближаться меньше, чем на определенное расстояние, и отдаляться более, чем на конкретную величину. В открытом космосе, где наблюдаются пустоши между галактиками, пространство особенно разряжено, это называется вакуумом. Тут гравитации нет в принципе, потому малое количество материи пребывает в хаосе. Возле очень плотных объектов (гигантские голубые звезды, квазары, а также черные дыры) сила притяжения поднимается до нереальных для нас, землян, величин. Частицы тут расположены настолько близко друг к другу, что образуется явление, которое называется «гравитационная сингулярность». Это та самая основа, влияющая на искажение пространства и степень кривизны. Гравитация и поведение материи В область сингулярности материя не засасывается. Туда притягивается только космический ветер и микроскопические частицы. Но человек чисто теоретически может по доброй воле отправиться в такие области. Они располагаются в квазарах и в черных дырах и, увы, для живых существ являются смертоносными с точки зрения биологии. Попадая в область большой приливной силы, тело начнет растягиваться как вдоль, так и поперек. В результате очертания человека окутают сферу и будут вращаться в ней. Теоретически, если глаза еще будут видеть и передавать сигнал в мозг, человек одновременно сможет лицезреть все свои части тела, включая лицо, которое будет вращаться перед ним, превышая скорость света. Понятно, что в таком виде человеческое тело существовать не может, но ведь это касается земной физики. Однако подобный пример дает нам возможность представить, что такое сингулярность с практической точки зрения. Было бы интересно предположить, что мы как биологический вид сможем принять эти новые физические законы и существовать в таких формах, образуя новые миры для себя.
Течение времени
О том, что такое время, можно спорить вечно. Сегодня его определяют как процесс прохождения физиологических, физических и психических процессов для живых организмов и материи нашего мира. Но свойства времени, его скрытые возможности так и не изучены. Мы воспринимаем его как нечто субъективное, и это тщательно можно отследить, вспоминая свои прошедшие годы. Когда мы проживали первый год жизни, этот отрезок для нас был равен 100 процентам. Он был единственным, что у нас есть, всей жизнью и опытом. На второй свой день рождения один год уже стал 50 процентами, на третий – лишь третью. К 80-летнему возрасту один год уже был лишь 1/80 частицей жизни и ничего практически не значил. Так случалось потому, что в течение первого года все, что мы видели, было новым. В дальнейшем нам попадались уже все более и более привычные вещи и явления. Потому и казалось, что детство тянется невероятно долго, а зрелые годы пролетают моментально. Это наглядный пример того, как восприятие одного человека искажает течение времени. А что же будет, если взглянуть на этот термин с астрономической точки зрения? Время в начале времен Это было небольшое отступление, которое дало возможность понять все то, что мы видим. Находясь запертыми в рамках физики и, более того, своего собственного восприятия, нам сложно представить, что мир был и может быть совсем другим. Так вот, сингулярность времени имела такое же место в космологии, как и сингулярность пространства. Сейчас для преодоления отрезка в 1 километр со скоростью 5 км/ч потребуется 0,2 часа. Чтобы долететь от Земли до Сатурна, необходимо затратить несколько лет. Но как быть с временем, если все расстояние, которое имеется в мире, равно 1 сантиметру? Умножая столь ничтожные параметры на бесконечно большую плотность и массу, мы получаем кривизну пространства-времени. Это означает, что в момент, когда Вселенная была сингулярной, могло происходить все то, что мы видим сейчас. События, возможно, перемешивались, невероятно искажались и сопоставлялись. Проще выражаясь, любой материальный объект мог заглянуть как в прошлое Земли или другой планеты, так и в ее будущее. Технологии и вступление в новую эру Существует и так называемая теория сингулярности, согласно которой наша планета скоро превратится в большой биотехнический интеллект. По мнению исследователей, к середине 21-го века будет создан компьютер, возможности которого превзойдут возможности мозга. Искусственный разум, естественно, возьмет верх над менее развитыми существами. В этот момент наступит технологическая сингулярность. Такое название было придумано потому, что неизвестно, чем такой прогрессивный скачок в области науки закончится и удастся ли выжить человечеству. Червоточины Сингулярность черной дыры, из которой, собственно, и состоит этот космический объект, – одна из самых больших загадок мира. Сама кротовая нора на самом деле выглядит не как яма с воронкой и узким тоннелем, а как сфера, образованная гигантской силой гравитации. О черных дырах мы уже говорили выше, определяя их как смертоносные объекты во Вселенной. Сила их сжатия невероятно велика, потому на горизонте событий искривляется пространство и останавливается время. Сингулярность черной дыры сравнима с теорией Большого взрыва. Досконально не изучено, но считается, что сила сжатия внутри червоточины такая же, как в момент зарождения мира. Вот почему бытует теория о том, что черные дыры – это эволюция новых Вселенных, которые существуют параллельно с нашей. Приложение, объясняющее часть теории В общих чертах теорию точки невозврата и бесконечной плотности дает понять игра «Сингулярность». Прохождение миссии связано с перемещением в пространстве и времени, где эти два понятия едины. Герой передвигается между 1950 годом и 2010-м, исправляя ошибки советских ученых и спасая современных каторжников, заключенных на острове, окруженном радиацией. Если погрузиться в этот мир, то постепенно можно понять, что значит время в пространственном измерении. Подведение итогов Изучение всех тайн космоса, которые касаются гравитации, дает возможность понять, что теория относительности нас предельно ограничивает. Конечно же, это невероятная находка для земных условий, но если речь идет об изучении иных пространств, то стоит отброс ить все стереотипы. Такое понятие, как «сингулярность», переворачивает восприятие звука, световых импульсов, кривизны пространства и длительности времени. Но встречается оно пока что только в математической теории, а в физической практике не находит себе объяснения. Наиболее детально ныне исследуется сингулярность черной дыры, но считается, что эта область хоть и сжата до бесконечности, это не самая сколлапсированная точка Вселенной.
Идея сингулярности перед Большим взрывом устарела

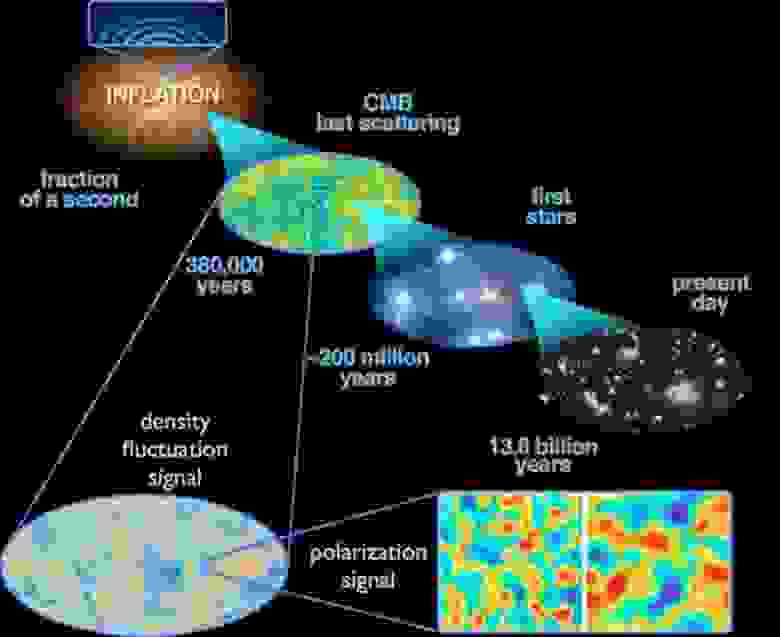
Иллюстрация нашей космической истории, от Большого взрыва и до сегодняшнего дня, в контексте расширяющейся Вселенной. Большому взрыву предшествовало состояние космической инфляции, но идея о том, что перед этим должна была существовать сингулярность, ужасно устарела.
Почти все слышали о Большом взрыве. Но если попросить разных людей, от обывателей до космологов, закончить предложение: «Вначале было…», вы получите множество различных ответов. Один из наиболее распространённых – «сингулярность», то есть, момент, когда вся материя и энергия Вселенной сконцентрировались в одной точке. Температура, плотность и энергия были бы сколь угодно, бесконечно большими, и это могло совпадать с зарождением самого пространства и времени.
Но эта картина не просто неверна, она уже лет 40, как устарела! Мы совершенно уверены в том, что с горячим Большим взрывом не было связано никакой сингулярности, и у пространства и времени могло вообще не быть момента зарождения. Вот, что нам известно, и откуда.

Астрономическое наблюдение GOODS-Север, проведённое при помощи телескопа Хаббл, позволило рассмотреть некоторые из наиболее удалённых галактик, которые мы когда-либо видели, многие из которых уже находятся на недостижимом для нас расстоянии. Заглядывая всё дальше и дальше, мы обнаруживаем, что наиболее удалённые галактики удаляются от нас всё быстрее и быстрее, благодаря расширению Вселенной.
Сегодняшняя Вселенная заполнена галактиками во всех направлениях и на разных расстояниях. В среднем, чем дальше от нас галактика, тем быстрее она удаляется от нас. Это происходит не из-за реального движения галактик в локальном для них космосе; всему виной расширение самой ткани пространства.
Такое предсказание было одним из необычных результатов, полученных из Общей теории относительности в 1922 году советским физиком Александром Фридманом, которое потом было подтверждено в наблюдениях Эдвина Хаббла и других учёных в 1920-х. Это означает, что с течением времени материя Вселенной рассредоточивается и становится менее плотной, поскольку объём Вселенной увеличивается. Это также означает, что в прошлом Вселенная была плотнее, горячее и более однородной.

Экстраполировав развитие назад, мы приходим к ранним более горячим и плотным состояниям. Приводит ли всё это к сингулярности, в которой перестают работать законы физики?
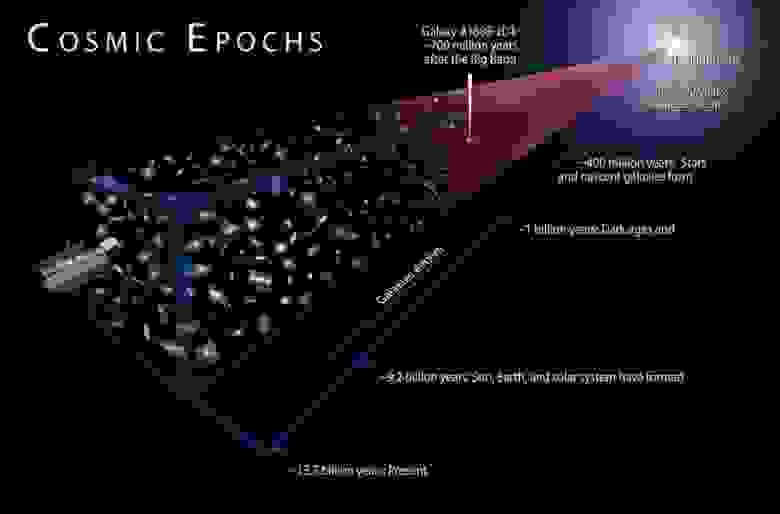
Звёзды и галактики, которые мы видим сегодня, не существовали всегда. Чем дальше мы пройдём назад по времени, тем ближе к сингулярности будет подходить Вселенная – но у экстраполяции есть свои ограничения.
Однако, если бы всё было именно так, и Вселенная в прошлом имела сколь угодно высокие температуры, у такого состояния было бы несколько явных признаков, которые можно было бы наблюдать и сегодня. В остаточном свечении Большого взрыва были бы температурные флуктуации огромных амплитуд. Видимые нами флуктуации были бы ограничены скоростью света, они появлялись бы только на масштабах, не больших космического горизонта. Должны были остаться реликты космоса высоких энергий, такие, как магнитные монополи.
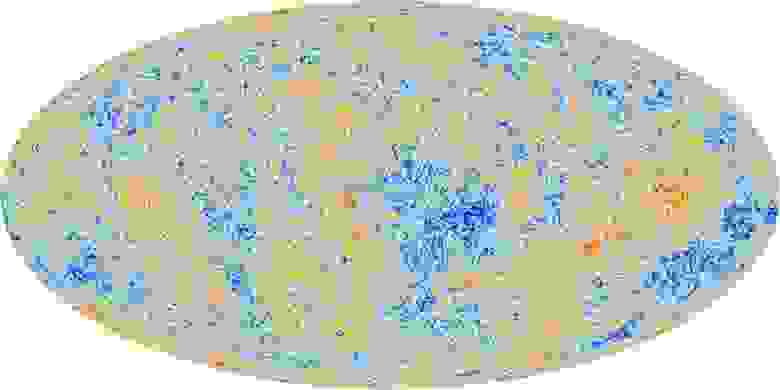
Флуктуации реликтового излучения настолько малы и настолько характерны, что из них определённо следует тот факт, что в начале Вселенной повсюду была одна и та же температура. Размер флуктуаций в 1/30 000 совершенно не соответствует Большому взрыву произвольной температуры.
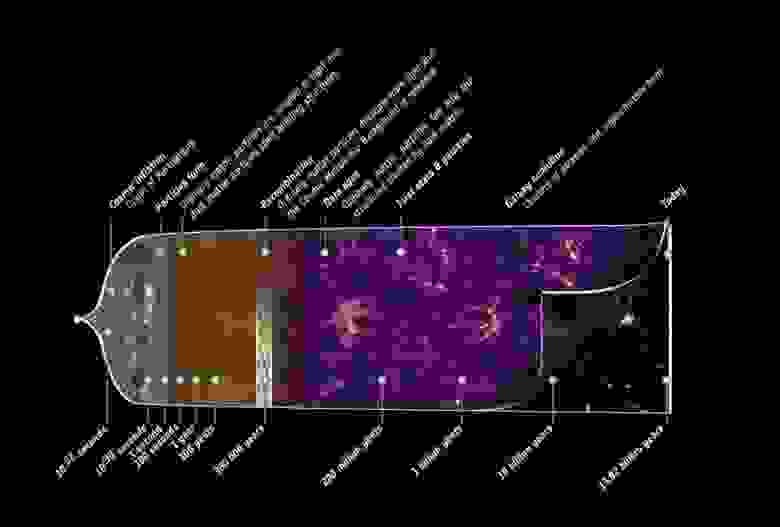
Космическая история известной Вселенной показывает, что происхождением всей материи и всего света внутри неё мы обязаны окончанию инфляции и началу горячего Большого взрыва. С тех пор 13,8 млрд лет шла космическая эволюция. Такую картину развития подтверждают большинство источников.
Что же породило инфляцию? На эту тему ведётся множество исследований и рассуждений, однако никто этого не знает. Не существует свидетельств, на которые можно было бы опереться, никаких наблюдений, которые можно было бы сделать, никаких экспериментов, которые можно было бы провести. Некоторые люди делают ошибочные заявления вроде:
Есть множество графиков и картинок, созданных ведущими космологами, иллюстрирующих данный сценарий. Но это не означает, что он верен.

Иллюстрация флуктуаций плотности (скаляр) и гравитационных волн (тензор), появившихся по окончанию инфляции. Предположение о существовании сингулярности до инфляции не обязательно будет верным.
Есть очень серьёзные основания полагать, что это не так! Мы можем математически продемонстрировать невозможность появления инфляционного состояния из сингулярности. И вот, почему: пространство во время инфляции расширяется с экспоненциальной скоростью. Представьте себе, как работает экспонента: по прошествии определённого количества времени Вселенная удваивает размер. Пройдёт в два раза больше времени, она удвоится два раза, то есть станет в четыре раза больше. Подождите три таких промежутка времени, и она удвоится три раза, то есть станет в 8 раз больше. Подождите 10 или 100 таких отрезков времени, и эти удвоения сделают Вселенную в 2 10 или 2 100 раз больше.
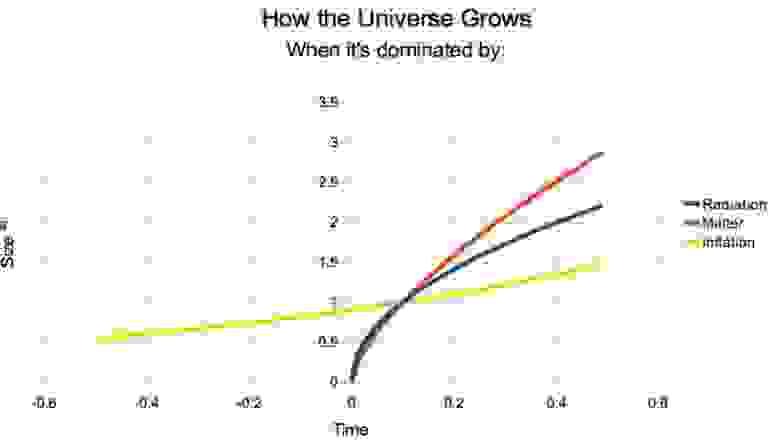
Синяя и красная линия – традиционный сценарий Большого взрыва, когда всё начинается в момент времени t=0, включая и само пространство-время. В инфляционном сценарии (жёлтый) мы никогда не приходим к сингулярности, в которой пространство принимает сингулярное состояние. Оно может стать сколько угодно малым в прошлом, а время продолжается бесконечно. Определить длительность этого состояния пытаются условие отсутствия границ Хокинга-Хартла и теорема Борда-Гута-Виленкина, но их нельзя назвать окончательными.
Среди космологов хорошо известна теорема, демонстрирующая неполноту прошлого инфляционного состояния. Это означает, что все частицы, существующие во Вселенной, испытывающей инфляцию, рано или поздно встретятся при экстраполяции назад по времени. Это, однако, не означает, что сингулярность обязательно существовала – просто инфляция не описывает всё, что происходило в истории Вселенной, например, её рождение. Нам также известно, что инфляция не может появиться из сингулярного состояния, поскольку испытывающий инфляцию участок всегда должен начинать с конечного размера.
Флуктуации пространства-времени на квантовом масштабе во время инфляции растягиваются по всей Вселенной, и порождают несовершенства в плотности и гравитационных волнах. Возникла ли инфляция из сингулярности, или нет, нам неизвестно.
И это – последний на Хабре перевод статьи Итана Сигеля (и в принципе статьи на тему космологии), поскольку тематику ресурса было решено сконцентрировать на разработке и IT.
Что такое сингулярность, или почему история человечества однажды станет непредсказуемой
Варламова Дарья
«Теории и практики» продолжают объяснять смысл часто употребляемых выражений, которые зачастую используются в разговорной речи в абсолютно неправильном значении. В очередном выпуске рубрики — что происходило в момент Большого Взрыва, что такое «принцип космической цензуры» и что станет с историей в постчеловеческую эру.
В философии слово «сингулярность», произошедшее от латинского «singulus» — «одиночный, единичный», обозначает единичность, неповторимость чего-либо — существа, события, явления. Больше всего над этим понятием размышляли современные французские философы — в частности, Жиль Делез. Он трактовал сингулярность как событие, порождающее смысл и носящее точечный характер. «Это поворотные пункты и точки сгибов; узкие места, узлы, преддверия и центры; точки плавления, конденсации и кипения; точки слез и смеха, болезни и здоровья, надежды и уныния, точки чувствительности». Но при этом, оставаясь конкретной точкой, событие неизбежно связано с другими событиями. Поэтому точка одновременно является и линией, выражающей все варианты модификации этой точки и ее взаимосвязей со всем миром.
Когда человек создаст машину, которая будет умнее человека, история станет непредсказуемой, потому что невозможно предугадать поведение интеллекта, превосходящего человеческий
В других науках термин «сингулярность» стал обозначать единичные, особые явления, для которых перестают действовать привычные законы. Например, в математике сингулярность — это точка, в которой функция ведет себя нерегулярно — например, стремится к бесконечности или не определяется вообще. Гравитационная сингулярность — это область, где пространственно-временной континуум настолько искривлен, что превращается в бесконечность. Принято считать, что гравитационные сингулярности появляются в местах, скрытых от наблюдателей — согласно «принципу космической цензуры», предложенному в 1969 году английским ученым Роджером Пенроузом. Он формулируется так: «Природа питает отвращение к голой (т.е. видимой внешнему наблюдателю) сингулярности». В черных дырах сингулярность скрыта за так называемым горизонтом событий — воображаемой границей черной дыры, за пределы которой не вырывается ничего, даже свет.
Но ученые продолжают верить в существование где-то в космосе «голых» сингулярностей. А самый яркий пример сингулярности — состояние с бесконечно большой плотностью материи, возникающее в момент Большого взрыва. Этот момент, когда вся Вселенная была сжата в одной точке, остается для физиков загадкой — потому, что он предполагает сочетание взаимоисключающих условий, например, бесконечной плотности и бесконечной температуры.
В сфере IT ждут прихода другой сингулярности — технологической. Ученые и обозначают этим термином тот переломный момент, после которого технический прогресс ускорится и усложнится настолько, что окажется недоступным нашему пониманию. Исходно этот термин предложил американский математик и Вернор Виндж в 1993 году. Он высказал следующую идею: когда человек создаст машину, которая будет умнее человека, история станет непредсказуемой, потому что невозможно предугадать поведение интеллекта, превосходящего человеческий. Виндж предположил, что это произойдет в первой трети XXI века, где-то между 2005 и 2030 годами.
В 2000 году американский специалист по развитию искусственного интеллекта Елиезер Юдковски также высказал гипотезу о том, что, возможно, в будущем появится программа искусственного интеллекта, способная совершенствовать саму себя со скоростью, во много раз превосходящей человеческие возможности. Близость этой эры, по мнению ученого, можно определить по двум признакам: растущая техногенная безработица и экстремально быстрое распространение идей.
«Вероятно, это окажется самой стремительной технической революцией из всех прежде нам известных, — писал Юдковски. — Свалится, вероятнее всего, как снег на голову — даже вовлеченным в процесс ученым… И что же тогда случится через месяц или два (или через ) после этого? Есть только одна аналогия, которую я могу провести — возникновение человечества. Мы очутимся в постчеловеческой эре. И несмотря на весь свой технический оптимизм, мне было бы куда комфортнее, если бы меня от этих сверхъестественных событий отделяли тысяча лет, а не двадцать».
Темой технологической сингулярности вдохновлялись писатели жанра «киберпанк» — например, она встречается в романе Уильяма Гибсона «Нейромант». Она показана и в популярном романе современного фантаста Дэна Симмонса «Гиперион» — там описывается мир, помимо людей, населенный Искинами — то есть, носителями искусственного интеллекта, которые вступают в конфликт с человечеством.
Неправильно «Это был сингулярный случай, когда механизм вышел из-под контроля». Правильно — «единичный».
Правильно «Я уверен, рано или поздно Вселенная снова схлопнется в сингулярность».
Правильно «Мне нравится этот роман — лучшее описание технологической сингулярности из всех, что я читал».
Существует ли сингулярность: от теории к фактам
Валерий Витальевич Васильев — российский ученый, академик РАН и специалист в области механики. На протяжении многих лет он изучает сингулярность решений прикладных задач, доказывая, что этот феномен — ни что иное как результат некорректности математической модели изучаемого явления или процесса. Попробуем разобраться в этом — существует ли сингулярность в реальности или она является формальным математическим результатом, не имеющим физического содержания.
Сразу отметим, что этот материал рассказывает об альтернативной концепции сингулярности. И её автор понимает, что она идёт вразрез с установившимися в науке концепциями. Соглашаться с ней или не соглашаться — личное дело каждого, но если вы не просто несогласны, но ещё и готовы своё несогласие аргументировать, мы приглашаем вас к дискуссии. А теперь обо всём по порядку.
Одна из наиболее распространенных сингулярностей связана с Черными дырами — загадочными областями пространства-времени, гравитационные аномалии которых привлекают к себе внимание ученых по всему миру. Теоретическая возможность существования подобных астрономических объектов, основанная на сингулярном решении сферически симметричной задачи общей теории относительности, обсуждается еще с начала прошлого века. Однако в связи с концепцией, согласно которой Черные дыры являются реально существующими объектами, сингулярность решения, из которого они следуют, связана с гораздо более общей проблемой — проблемой реальности сингулярных решений прикладных задач. Решению этой проблемы посвятил свою работу Валерий Витальевич Васильев — советский и российский ученый, академик РАН, специалист в области строительной механики, теории упругости и проектирования конструкций из композитных материалов.
Сингулярность: что это такое
Валерий Витальевич Васильев
Как известно, исследование реальных процессов и явлений всегда осуществляется в рамках их физических моделей, описываемых некоторыми уравнениями, образующими математическую модель. Эти модели соответствуют реальности лишь приближенно, поскольку исследователи традиционно не учитывают множество второстепенных факторов, значительно усложняющих анализ. Если при решении уравнений, описывающих математическую модель, не привлекается дополнительных упрощений, то получаемое решение считается точным. Однако это справедливо только в отношении модели и только в рамках традиционного математического анализа, допускающего возможность существования бесконечно малых и бесконечно больших величин. Последние и появляются в сингулярных решениях в так называемых точках сингулярности.
Сингулярность — это свойство функций обращаться в бесконечность в отдельных точках. В 1916 году немецкий астроном Карл Шварцшильд представил решение уравнений общей теории относительности для задачи о гравитации, создаваемой покоящимся шаром. В последующей интерпретации решения Шварцшильда была обнаружена поверхность в пространстве, на которой гравитация оказывается бесконечно большой, т. е. имеет место сингулярность иногда называемая сингулярностью Шварцшильда.
Следует обратить внимание на то, что большинство исследователей, по словам Валерия Васильева, придерживается умеренной трактовки сингулярности, согласно которой решение считается справедливым везде за исключением точки сингулярности, в которой оно не соответствует реальности. Именно такой интерпретации придерживался и создатель теории относительности Альберт Эйнштейн, с восторгом встретивший решение Шварцшильда. Великий физик полагал, что в окрестности точки сингулярности его теория не описывает гравитацию и, как следствие, применять ее в данном случае некорректно.
Академик Васильев отмечает, что с примерно с 60-х годов XX века ситуация в физике радикально изменилась: возобладало мнение, что сингулярность реально существует в природе. В результате этого были введены астрономические объекты, названные Черными дырами, обладающие бесконечно большой гравитацией. Согласно одной из современных интерпретаций решения задачи Шварцшильда, Черная дыра — это сферическая область пространства, в центре которой сосредоточена масса и где решение сингулярно. Эта центральная точка окружена сферой, радиус которой rg зависит от массы — это так называемый радиус горизонта событий Черной дыры. Если наблюдатель каким-то образом проникнет за грань горизонта событий, дальнейшее движение будет возможно только к центру. Обратное движение невозможно даже для света и Черная дыра невидима.
Однако, поскольку сосредоточение массы в точке (в абстрактном, сугубо математическом объекте) представляется нереалистичным, возможна и другая концепция, согласно которой в центре гипотетической Черной дыры находится шар. Согласно решению задачи Шварцшильда для шара, состоящего из идеальной жидкости, в центре этого шара сингулярность отсутствует — она смещается на поверхность шара R = rg и, как следствие, гравитация на этой поверхности становится бесконечно большой. Благодаря этому Черная дыра становится невидимой: гравитация так велика, что вторая космическая скорость на поверхности шара становится равной скорости света и фотоны не могут покинуть эту поверхность.
Две возможные концепции Черной дыры
Валерий Васильев отмечает, что в настоящее время основное внимание уделяется «внешней задаче Шварцшильда» для окружающего шар пространства и практически не обсуждается «внутренняя задача» для области внутри шара. Однако для получения полного решения необходимо решить обе эти задачи и удовлетворить граничные условия на поверхности шара. Существенно, что в общем случае система уравнений, предложенных Эйнштейном, отличается не только сложностью, но и отсутствием полной взаимной независимости — независимы друг от друга лишь 6 из 10 уравнений, включающих 10 неизвестных функций. Остальные 4 уравнения пока остаются неизвестными, несмотря на многочисленные попытки выдающихся ученых получить их. Таким образом, неизвестных в системе больше, чем уравнений — система Эйнштейна осталась незавершенной. Для получения решения задачи о шаре неполная система исходных уравнений Эйнштейна (их в этом случае три, но взаимно независимыми являются только два, включающие три неизвестных функции) должна быть дополнена еще одним уравнением. В настоящее время это дополнение осуществляется таким образом, что внешнее решение, являющееся сингулярным, получается независимо от внутреннего решения. Но этого не должно быть — внешнее решение должно сшиваться с внутренним на поверхности шара. Если продолжить анализ и построить внутреннее решение, то можно обнаружить, что при введенном дополнительном уравнении граничное условие на поверхности шара не выполняется. Это условие можно изменить так, чтобы граничное условие выполнялось. Но тогда решение не является сингулярным и определяет не Черные дыры, а так называемые Темные звезды, теоретически открытые в конце 18 века Джоном Мичеллом и Пьером-Симоном Лапласом. Они также невидимы, но не обладают всепоглощающей сингулярностью и их гравитация описывается уравнениями общей теории относительности.
Сингулярность в механике сплошной среды — теории и факты
Большое количество сингулярных решений известно в механике твердого деформируемого тела. Например, в задаче об изгибе круглой мембраны (пленки, натянутой на барабан) силой, приложенной в центре, прогиб мембраны в центре оказывается бесконечно большим. Несоответствие с реальностью связано с неадекватностью традиционной физической модели мембраны, согласно которой она не обладает изгибной жесткостью. Если эту жесткость учесть, сингулярность исчезает и решение полностью согласуется с экспериментом.
В задаче о растяжении пластины с трещиной существующее решение дает на концах трещины бесконечно большие напряжения при сколь угодно малой нагрузке, действующей на пластину. Теоретически хрупкие тела с трещинами существовать не могут, однако это не так — оконное стекло с трещиной может служить долго. Для преодоления этого противоречия построена специальная наука — механика хрупкого разрушения, которой посвящена обширная литература. Однако дело оказалось не в теории, а в математической модели сплошной среды, основанной на классическом дифференциальном исчислении, допускающим существование бесконечно малых и бесконечно больших величин. Если построить его модификацию, не допускающую существование бесконечно малых и больших, величин, то такая модель сплошной среды исключает появление сингулярных решений и приводит к результатам, хорошо согласующимся с экспериментальными.
Подводя итог, следует отметить, что в свете всего вышесказанного само существование сингулярности в реальном мире видится академику Васильеву нереалистичным. Он объясняет интерес к сингулярным решениям кажущейся математической строгостью и совершенством — но математика, основанная законах логики, увы, не всегда соответствует действительности, и для науки гораздо важнее полагаться на истину, критерием которой в прикладных задачах является эксперимент.


