И тогда геометрическая сумма токов не обратится в ноль, а значит и в нейтральном проводнике будет иметь место переменный ток, поэтому нейтральный проводник в данном случае необходим. Примеры несимметричных нагрузок: лампы накаливания разной мощности в трех фазах, несимметрично нагруженный трехфазный трансформатор, нагрузки с разными коэффициентами мощности в трех фазах и т. д.

Нейтральный провод в данном случае обеспечит сохранение симметрии фазных напряжений несмотря на то, что нагрузка несимметрична. Вот почему четырехпроводная сеть допускает включение однофазных потребителей различной мощности и характера импеданса в разные фазы. Цепь каждой нагруженной фазы будет находится под фазным напряжением генератора независимо от разницы нагрузок между фазами.

Здесь изображена векторная диаграмма несимметричной нагрузки. На диаграмме легко видеть, что за счет наличия нулевого провода, ток в нем представляет собой геометрическую сумму векторов токов каждой из фаз, при этом фазные напряжения не испытывают перекоса, который непременно бы возник если бы нулевого провода при несимметричной нагрузке не было.

Если по какой-нибудь причине нейтральный провод оборвется во время питания несимметричной нагрузки, то возникнет резкий перекос напряжений и токов трехфазной сети, который может привести к аварии.

Перекос случится в этом случае потому, что три цепи нагрузки, питаемые трехфазным источником, вместе со внутренним сопротивлением источника, образуют три цепи разного импеданса, падение напряжения на каждой из которых будет разным и система напряжений трехфазной сети перестанет поэтому быть симметричной. Подробнее об этом смотрите здесь: Причины и последствия обрыва нулевого провода в электросети

Источник

Симметричная нагрузка

Нагрузка считается симметричной, когда равны в отдельности активные и реактивные составляющие сопротивлений всех фаз:

.

Через комплексные значения полных сопротивлений фаз условие симметричности нагрузки:

В отношении любой фазы справедливы все формулы, полученные для однофазных цепей. Например, для фазы а:

(5)

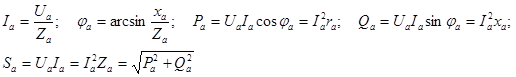
Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена на рис. 1,б.

Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов. Поэтому ток в нейтральном проводе

. (6)

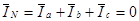
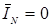
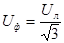
Очевидно, отключение нейтрального провода при не приведет к изменению фазных напряжений, токов, углов сдвига фаз, мощностей и векторной диаграммы. Даже при отсутствии нейтрального провода фазные напряжения оказываются равными , т.е. тому напряжению, на которое рассчитаны фазы трехфазного приемника.

При симметричной нагрузке в нейтральном проводе нет необходимости, и в этом случае он не применяется.

Мощности трехфазного приемника могут быть выражены:

(7)

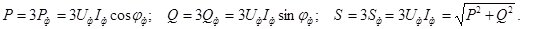
В качестве номинальных напряжений и токов трехфазных приемников указывают обычно линейные напряжения и токи. Учитывая это, мощности трехфазных приемников целесообразно также выражать через линейные напряжения и токи, т.е.

(8)

Источник

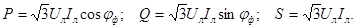
Таким образом, понятие «фаза» имеет в электротехнике два значения:

Цепи в зависимости от количества фаз называют

Трехфазные цепи – наиболее распространенные в современной электроэнергетике. Это объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями:

экономичность производства и передачи энергии по сравнению с однофазными цепями;

возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя;

возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.

Трехфазная цепь состоит из трех основных элементов :

линии передачи со всем необходимым оборудованием;

Трехфазный генератор представляет собой синхронную машину двух типов: турбогенератор и гидрогенератор.

Модель трехфазного генератора схематически изображена на рис. 3.1.

На статоре 1 генератора размещается обмотка 2, состоящая из трех частей или, как их принято называть, фаз. Обмотки фаз располагаются на статоре таким образом, чтобы их магнитные оси были сдвинуты в пространстве относительно друг друга на угол 2π/3, т.е. на 120°. На рис. 3.1 каждая фаза обмотки статора условно показана состоящей из одного витка. Начала фаз обозначены буквами A, B и C, а концы –X, Y, Z. Ротор 3 представляет собой электромагнит, возбуждаемый постоянным током обмотки возбуждения 4, расположенной на роторе.

При вращении ротора турбиной с равномерной скоростью в обмотках фаз статора индуктируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся друг от друга по фазе на 120° вследствие их пространственного смещения.

На схеме обмотку (или фазу) источника питания изображают как показано на рис. 3.2.

За условное положительное направление ЭДС в каждой фазе принимают направление от конца к началу. Обычно индуктированные в обмотках статора ЭДС имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на один и тот же угол 120°. Такая система ЭДС называется симметричной.

Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного.

Графики мгновенных значений трехфазной симметричной системы ЭДС показаны на рис. 3.3.

Если ЭДС одной фазы (например, фазы A) принять за исходную и считать её начальную фазу равной нулю, то выражения мгновенных значений ЭДС можно записать в виде

Из графика мгновенных значений (рис 3.3) следует

Комплексные действующие ЭДС будут иметь выражения:

Ė_A=E_me j 0 ° =E_m(1+j0), Ė_B=E_me − j 120 ° =E_m(−1/2−j/2), Ė_C=E_me + j 120 ° =E_m(−1/2+j/2).

Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис 3.4а.

На диаграмме рис. 3.4а вектор Ė_A направлен вертикально, так как при расчете трехфазных цепей принято направлять вертикально вверх ось действительных величин. Из векторных диаграмм рис 3.4 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю:

Последовательность фаз определяет направление вращения трехфазных двигателей. Для определения последовательности фаз имеются специальные приборы – фазоуказатели.

В период зарождения трехфазных систем имелись попытки использовать несвязанную систему, в которой фазы обмотки генератора не были электрически соединены между собой и каждая фаза соединялась со своим приемником двумя проводами (рис. 3.5). Такие системы не получили применения вследствие их неэкономичности: для соединения генератора с приемником требовалось шесть проводов (рис. 3.5)

Более совершенными и экономичными являются связанные цепи, в которых фазы обмотки электрически соединены между собой.

Существуют различные способы соединения фаз трехфазных источников питания и трехфазных потребителей электроэнергии.

Наиболее распространенными являются соединения «звезда» и «треугольник». При этом способ соединения фаз источников и фаз потребителей в трехфазных системах могут быть различными. Фазы источника обычно соединены «звездой», фазы потребителей соединяются либо «звездой», либо «треугольником».

Соединение фаз генератора и приемника звездой

При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Z_a, Z_b, Z_c) также соединяют в одну точку n. Такое соединение называется соединение звезда.

Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.

В трехфазных цепях различают фазные и линейные напряжения.

За условно положительные направления фазных напряжений принимают направления от начала к концу фаз.

Линейное напряжение (U_Л) – напряжение между линейными проводами или между одноименными выводами разных фаз (U_AB, U_BC, U_CA).

Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).

По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:

Фазные (I_Ф) – это токи в фазах генератора и приемников.

При соединении в звезду фазные и линейные токи равны

Ток, протекающий в нейтральном проводе, обозначают I_N.

По первому закону Кирхгофа для нейтральной точки n (N) имеем в комплексной форме

İn=ia+ib+ic.

В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа.

Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: U_AB, U_BC,U_CA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение U_Л), и опережают, соответственно, векторы фазных напряжений U_A, U_B, U_C, (U_Ф) на угол 30°.

Действующие значения линейных напряжений можно определить графически по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений:

U_Л=U_Ф.

Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями:

Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи.

Классификация приемников в трехфазной цепи

Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:

Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Z_a = Z_b = Z_c, то трехфазный приемник называют равномерным, если φ_a = φ_b = φ_c, то однородным.

Четырехпроводная цепь

Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому для упрощения расчетов таких цепей (если не требуется большая точность) сопротивления проводов можно не учитывать (Z_Л = 0, Z_N = 0). Тогда фазные напряжения приемника U_a, U_b и U_cбудут равны соответственно фазным напряжениям источника электрической энергии(генератора или вторичной обмотки трансформатора), т.е. U_a = U_A; U_b = U_B; U_c = U_C. Если полные комплексные сопротивления фаз приемника равны Z _a = Z _b = Z _c, то токи в каждой фазе можно определить по формулам

İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.

В соответствии с первым законом Кирхгофа ток в нейтральном проводе

İn = İa + İb + İc = ia + ib + ic.

Симметричная нагрузка приемника

При симметричной системе напряжений и симметричной нагрузке, когда Z _a = Z _b = Z _c, т.е. когда R_a = R_b = R_c = R_ф и X_a = X_b = X_c = X_ф, фазные токи равны по значению и углы сдвига фаз одинаковы

Ia = Ib = Ic = Iф = Uф / Zф,

Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İ_a + İ_b + İ_c = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе I_N = 0, поэтому необходимость в нейтральном проводе отпадает.

Несимметричная нагрузка приемника

При симметричной системе напряжений и несимметричной нагрузке, когда Z_a ≠ Z_b ≠ Z_c и φ_a ≠ φ_b ≠ φ_c токи в фазах потребителя различны и определяются по закону Ома

İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.

Ток в нейтральном проводе İ_N равен геометрической сумме фазных токов

İn = İa + İb + İc.

Напряжения будут U_a = U_A; U_b = U_B; U_c = U_C, U_Ф = U_Л / , благодаря нейтральному проводу при Z_N = 0.

Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.

Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.

Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9

Трехпроводная электрическая цепь

Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.

При симметричной нагрузке, когда Z _a = Z _b = Z _c = Z_φ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, U_nN = 0.

Соотношение между фазными и линейными напряжениями приемника также равно , т.е. U_Ф = U_Л / , а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).

При несимметричной нагрузке Z _a ≠ Z _b ≠ Z _c между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали U_nN.

Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,

,

где: Y _a = 1 / Z _a; Y _b = 1 / Z _b; Y _c = 1 / Z _c – комплексы проводимостей фаз нагрузки.

Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что

Зная фазные напряжения приемника, можно определить фазные токи:

İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc.

Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и U_nN (рис. 3.11).

При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали U_nN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Ú_a, Ú_b и Ú_c могут отличаться друг от друга весьма существенно.

Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Ú_a, Ú_b, Ú_c и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).

Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.

Поэтому нейтральный провод необходим для того, чтобы:

выравнивать фазные напряжения приемника при несимметричной нагрузке;

подключать к трехфазной цепи однофазные приемники с номинальным напряжением в раз меньше номинального линейного напряжения сети.

Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.

Соединение фаз генератора и приемника треугольником

При соединении источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началом В второй фазы, конец Y второй фазы – с началом С третьей фазы, конец третьей фазы Z – c началом первой фазы А. Начала А, В и С фаз подключаются с помощью трех проводов к приемникам.

Соединение фаз источника в замкнутый треугольник возможно при симметричной системе ЭДС, так как

Если соединение обмоток треугольником выполнено неправильно, т.е. в одну точку соединены концы или начала двух фаз, то суммарная ЭДС в контуре треугольника отличается от нуля и по обмоткам протекает большой ток. Это аварийный режим для источников питания, и поэтому недопустим.

Напряжение между концом и началом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению.

Пренебрегая сопротивлением линейных проводов, линейные напряжения потребителя можно приравнять линейным напряжениям источника питания: U_ab = U_AB, U_bc = U_BC, U_ca = U_CA. По фазам Z_ab, Z_bc, Z_caприемника протекают фазные токи İ_ab, İ_bc и İ_ca. Условное положительное направление фазных напряжений Ú_ab, Ú_bc и Ú_ca совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов İ_A, İ_B и İ_C принято от источников питания к приемнику.

В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Токи в фазах приемника определяются по формулам

İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.

Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c (рис 3.12)

Сложив левые и правые части системы уравнений, (3.20), получим

т.е. сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке.

Симметричная нагрузка

При симметричной нагрузке

Так как линейные (они же фазные) напряжения U_AB, U_BC, U_CA симметричны, то и фазные токи образуют симметричную систему

Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°.

образуют также симметричную систему токов (рис.3.13, 3.14).

На векторной диаграмме (рис. 3.14) фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что напряжение U_AB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в раз. Линейный ток İ_A отстает по фазе от фазного тока İ_ab на угол 30°, на этот же угол отстает İ_B от İ_bc, İ_C от İ_ca.

Таким образом, при соединении треугольником действующее значение линейного тока при симметричной нагрузке в раз больше действующего значения фазного тока и U_Л = U_Ф; I_Л =I_Ф.

При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы.

Фазное напряжение U_Ф = U_Л. Фазный ток I_Ф = U_Ф / Z_Ф, линейный ток I_Л =I_Ф, угол сдвига по фазе φ = arctg (X_Ф / R_Ф).

Несимметричная нагрузка приемника

В общем случае при несимметричной нагрузке Z_ab ≠ Z_bc ≠ Z_ca. Обычно она возникает при питании от трехфазной сети однофазных приемников. Например, для нагрузки, рис. 3.15, фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными.

Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активно-емкостная приведена на рис. 3.16, топографическая диаграмма – на рис. 3.17.

Построение векторов линейных токов произведено в соответствии с выражениями

Таким образом, при несимметричной нагрузке симметрия фазных токов İ_ab, İ_bс, İ_ca нарушается, поэтому линейные токи İ_A, İ_B, İ_C можно определить только расчетом по вышеприведенным уравнениям (3.20) или найти графическим путем из векторных диаграмм (рис. 3.16, 3.17).

Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки.

При расчете для несимметричной нагрузки сначала определяют значения фазных токов İ_ab, İ_bc, İ_ca и соответствующие им сдвиги фаз φ_ab, φ_bc, φ_ca. Затем определяют линейные токи с помощью уравнений (3.20) в комплексной форме или с помощью векторных диаграмм (рис. 3.16, 3.17).

Общие замечания к расчету трехфазных цепей

1. При расчете трехфазных цепей исходят из предположения, что генератор дает симметричную систему напряжений. На практике несимметрия нагрузки практически не влияет на систему напряжений генератора в том случае, если мощность нагрузки мала по сравнению с мощностью генератора или сети электроснабжения.

2. Схема соединения обмоток трехфазного генератора не предопределяет схему соединения нагрузки. Так, при соединении фаз генератора в звезду нагрузка может быть соединена в звезду с нейтральным проводом, в звезду без нейтрального провода или, наконец, в треугольник.

Мощность трехфазной цепи, ее расчет и измерение

В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей.

Соединение потребителей звездой

В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз

Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз

Полная мощность отдельных фаз

Полная мощность трехфазного приемника

.

Активная мощность симметричного трехфазного приемника

Аналогично выражается и реактивная мощность

Отсюда следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат.

Соединение потребителей треугольником

В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз

Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз

Полная мощность отдельных фаз

Полная мощность трехфазного приемника

.

Активная мощность симметричного трехфазного приемника

Аналогично выражается и реактивная мощность

Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через линейные величины U_Л и I_Л.

При соединении фаз симметричного приемника звездой U_Ф = U_Л / , I_Ф = I_Л, при соединении треугольником U_Ф = U_Л, I_Ф = I_Л / . Поэтому независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой

P = U_Л I_Л cos φ.

где U_Л и I_Л – линейное напряжение и ток; cos φ – фазный.

Обычно индексы «л» и «ф» не указывают и формула принимает вид

P = U I cos φ.

Соответственно реактивная мощность

Q = U I sin φ.

S = U I.

При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током, и, что при неизмененном линейном напряжении, переключая приемник со звезды в треугольник его мощность увеличивается в три раза:

Измерение активной мощности в трехфазных цепях

Измерение активной мощности в трехфазных цепях производят с помощью трех, двух или одного ваттметров, используя различные схемы их включения. Схема включения ваттметров для измерения активной мощности определяется схемой сети (трех- или четырехпроводная), схемой соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная), доступностью нейтральной точки.

При несимметричной нагрузке в четырехпроводной цепи активную мощность измеряют тремя ваттметрами (рис. 3.18), каждый из которых измеряет мощность одной фазы – фазную мощность.

Активная мощность приемника определяют по сумме показаний трех ваттметров

Измерение мощности тремя ваттметрами возможно при любых условиях.

При симметричном приемнике и доступной нейтральной точке активную мощность приемника определяют с помощью одного ваттметра, измеряя активную мощность одной фазы P_Ф по схеме рис. 3.19. Активная мощность всего трехфазного приемника равна при этом утроенному показанию ваттметра: P = 3 P_Ф.

На рис. 3.19 показано включение прибора непосредственно в одну из фаз приемника. В случае, если нейтральная точка приемника недоступна или зажимы фаз приемника, включенного треугольником не выведены, применяют схему рис. 3.20 с использованием искусственной нейтральной точки n’. В этой схеме дополнительно в две фазы включают резисторы с сопротивлением R = R_V.

Измерение активной мощности симметричного приемника в трехфазной цепи одним ваттметром применяют только при полной гарантии симметричности трехфазной системы.

Измерение активной мощности двумя ваттметрами

В трехпроводных трехфазных цепях при симметричной и несимметричной нагрузках и любом способе соединения приемников широко распространена схема измерения активной мощности приемника двумя ваттметрами (рис. 3.21). Показания двух ваттметров при определенной схеме их включения позволяют определить активную мощность трехфазного приемника, включенного в цепь с симметричным напряжением источника питания.

На рис. 3.21 показана одна из возможных схем включения ваттметров: здесь токовые катушки включены в линейные провода с токами I_A и I_B, а катушки напряжения – соответственно на линейные напряжения U_AC и U_BC.

Докажем, что сумма показаний ваттметров, включенных по схеме рис. 3.21, равна активной мощности Р трехфазного приемника. Мгновенное значение общей мощности трехфазного приемника, соединенного звездой,

Источник