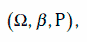что такое сечение случайного процесса

Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы.

Случайным (стохастическим, вероятностным) процессом называется функция действительного переменного t, значениями которой являются соответствующие случайные величины X(t).

В теории случайных процессов t трактуется как время, принимающее значения из некоторого подмножества Т множества действительных чисел (t T, T R).

В рамках классического математического анализа под функцией y=f(t) понимается такой тип зависимости переменных величин t и y, когда конкретному числовому значению аргумента t соответствует и притом единственное числовое значение функции y. Для случайных процессов ситуация принципиально иная: задание конкретного аргумента t приводит к появлению случайной величины X(t) с известным законом распределения (если это дискретная случайная величина) или с заданной плотностью распределения (если это непрерывная случайная величина). Другими словами, исследуемая характеристика в каждый момент времени носит случайный характер с неслучайным распределением.

Значения, которые принимает обычная функция y=f(t) в каждый момент времени, полностью определяет структуру и свойства этой функции. Для случайных процессов дело обстоит иным образом: здесь совершенно не достаточно знать распределение случайной величины X(t) при каждом значении t, необходима информация об ожидаемых изменениях и их вероятностях, то есть информация о степени зависимости предстоящего значения случайного процесса от его предыстории.

Наиболее общий подход в описании случайных процессов состоит в задании всех его многомерных распределений, когда определена вероятность одновременного выполнения следующих событий:

t₁, t₂,…,t_n T, n N: X(t_i)≤x_i; i=1,2,…,n;

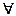
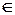
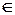
Неслучайная числовая функция x(t)=X(t, ω₀) называется реализацией (траекторией) случайного процесса X(t, ω).

Сечением случайного процесса X(t, ω) называется случайная величина, которая соответствует значению t=t₀.

Если аргумент t принимает все действительные значения или все значения из некоторого интервала T действительной оси, то говорят о случайном процессе с непрерывным временем. Если t принимает только фиксированные значения, то говорят о случайном процессе с дискретным временем.

В общем случае задать случайный процесс аналитически невозможно. Исключение составляют так называемые элементарные случайные процессы, вид которых известен, а случайные величины входят как параметры:

Источник

Случайные процессы и их основные характеристики

Дано основное вероятное пространство

где Ω – пространство элементарных событий;

β – σ-алгебра случайных событий;

Р – вероятностная мера.

Рассмотрим некоторое числовое множество V, элементы которого в дальнейшем будем считать моментами времени.

т. е. является случайным событием.

Из условия (1) следует, что если на множестве V определен случайный процесс ξ(w, t), то каждому моменту времени t ∈ V поставлена в соответствие случайная величина ξt(w) = ξ(w, t). Случайная величина ξt(w) называется сечением случайного процесса в момент времени t.

Таким образом, чтобы на множестве V задать некоторый случайный процесс, достаточно каждому моменту времени t ∈ V поставить в соответствие ту или иную случайную величину ξt(w) – сечение этого случайного процесса. В силу этого случайный процесс можно обозначить как ξt(w) или просто ξt.

Пример 1. Рассмотрим случайный процесс

Сечением данного случайного процесса в момент времени t = 2 является случайная величина 2η(w) + 1. Траектории случайного процесса ξ(w, t) изображены на рис. 1.

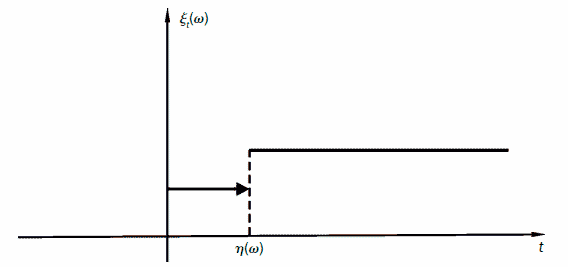
Пример 2. Случайный процесс на [0, +?) определен следующим образом:

Сечением случайного процесса ξ(w, t) в момент времени t является случайная величина, принимающая значение 1 с вероятностью, равной P <η(w) >t>, и значение 2 с вероятностью, равной P<η(w) ≤ t>.

Траектория случайного процесса ξ(w, t) имеет вид, изображенный на рис.2. Важнейшими характеристиками случайных процессов являются математическое ожидание и дисперсия.

Пример 3. Найдем математическое ожидание и дисперсию случайного процесса из примера 1.

Рис. 1. Траектория случайного процесса из примера 1

Рис. 2. Траектория случайного процесса из примера 2

Источник

Лекции 4,5. Случайные процессы и их основные статистические характеристики

1.Понятие случайного процесса.

2.Реализации и сечения случайного процесса.

3.Функции распределения и плотности вероятности СП.

4.Белый шум и марковский СП.

5.Статистические характеристики СП.

Функцию, значение которой при каждом значении независимой пере­менной является случайной величиной, называют случайней функцией. Случайные функции, для которых независимой переменной является время, называют случайными процессами или стохастическими про­цессами. Поскольку в автоматических системах управления процессы протекают во времени, то в дальнейшем будут рассматриваться только случайные процессы.

Рассмотрим, например, случайный дрейф на выходе усилителя по­стоянного тока при входном напряжении, равном нулю. Чтобы изу­чить характеристики дрейфа, можно взять, например, п одинаковых усили­телей, поместить их в одинаковые условия работы, одновременно включить и получить п осциллограмм дрейфа на выходах усилителей. Совокупность всех осциллограмм образует случайный процесс X(t>, a каждая из осциллограмм является конкретной реа­лизацией x,(f) случайного процесса.

Для любого фиксиро­ванного момента времени, например t = t_i, реализа­ция случайного процесса Xi(t_i> представляет собой конкретную величину, зна­чение же случайной функ­ции X(/i) является случай­ной величиной,называемой сечением случайного про­цесса в момент времени tx. Поэтому нельзя утвер­ждать, что случайный про­цесс в данный момент времени имеет такое-то детерминированное значение, можноговоритьлишь о вероятности того, что в данный момент времени значение слу­чайного процесса как случайной величины будет находиться в оп­ределенных пределах.

Статистические методы изучают не каждую из реализации x, образующих множество X(t>, а свойства всего множества в целом при помощи усреднения свойств входящих в него реализации. Поэтому при исследовании автоматической системы управления судят о ее поведе­нии не по отношению к какому-либо определенному воздействию, пред­ставляющему заданную функцию времени, а по отношению к целой совокупности воздействий.

Как известно, статистические свойства случайной величины х определяют по ее функции распределения (интегральному закону распределения) F(x) или плотности вероятности (дифференциальному закону распределения) w(x).

Случайные величины могут иметь различные законы распределения: равномерный, нормальный, экспоненциальный и др. Во многих зада­чах автоматического, управления очень часто приходится иметь дело с нормальным законом распределения (или законом Гаусса), который получается, если случайная величина определяется суммарным эффек­том от действия большого числа различных независимых факторов.

Для случайного процесса также вводят понятие функции распределения F(x, t) и плотности вероятности и>(х, /), которые зависят от фиксированного момента времени наблюдения t иот некоторого выбранного уровня х, т. е. являются функциями двух переменных х и t.

Рассмотрим случайную величину X(t_i), т. е. сечение случайного процесса в момент времени t_i. Одномерной функцией распределения (функцией распределения первого порядка) случайного процесса X(t) называют вероятность того, что текущее значение случайного процесса X(t_i) в момент времени t_i не превышает некоторого заданного уровня (числа) X_i, т. е.

то функцию w_i(X_i, t_i) называют одномерной плотностью вероятности (плотностью вероятности первого порядка) случайного процесса. Ве­личина

представляет собой вероятность того, что X(t) находится в момент вре­мени t == t_i в интервале от X_i до X_i + dx_i.

Функции F_i(x, t) и w(x, t) являются простейшими статистическими характеристиками случайного процесса. Они характеризуют случай­ный процесс изолированно в отдельных его сечениях, не раскрывая взаимной связи между сечениями случайного процесса, т. е. между возможными значениями случайного процесса в различные моменты времени.

Знания этих функций еще недостаточно для описания случайного процесса в общем случае. Необходимо охарактеризовать также взаим­ную связь случайных величин в различные произвольно взятые моменты времени.

называют двумерной функцией распределения (функцией распределения второго порядка). Если функция F₂(x₁, t₁; x₂, t₂) имеет частные произ­водные по x₁ и x₂, т.е.

то функцию w₂(x₁, t₁; x₂, t₂) называют двумерной плотностью вероятности (плотностью вероятности второго порядка.) Величина

Аналогично можно ввести понятие о п-мерной функции распре­деления:

Если функция F_n имеет частные производные по всем аргументам

то функцию w_n называют п-мерной плотностью вероятности.

Чем выше порядок п, тем полнее описываются статистические свойства случайного процесса. Зная п-мерную функцию распреде­ления, можно найти по ней одномерную, двумерную и другие (вплоть до (n-1)-й) функции распределения более низкого порядка. Однако многомерные законы распределения случайных процессов являются сравнительно громоздкими характеристиками и с ними крайне трудно оперировать на практике. Поэтому при изучении случайных процессов часто ограничиваются случаями, когда для описания случайного про­цесса достаточно знать только его одномерный или двумерный закон распределения.

Примером случайного процесса, который полностью характеризуется одно­мерной плотностью вероятности, является так называемый чистый случайный процесс, или белый шум. Значения Х(t) в этом процессе, взятые в разные момен­ты времени t, совершенно независимы друг от друга, как бы близко ни были вы­браны эти моменты времени. Это означает, что кривая белого шума содержит всплески, затухающие за бесконечно малые промежутки времени. Поскольку значения X(t), например, в моменты времени t₁ и t₂ независимы, то вероятность совпадения событий, заключающихся в нахождении Х(t) между x₁ и x₁+dx₁ в момент времени t₁ и между x₂ и x₂+dx₂ в момент t₂, равна произведению вероят­ностей каждого из этих событий, поэтому

Н вообще для белого шума

т. е. все плотности вероятности белого шума определяются из одномерной плотности вероятности.

Для случайных процессов общего вида, если известно, какие значения при­няла величина Х(t_k) в момент времени t_k, тем самым имеем некоторую информа­цию относительно Х(t_m), где m>k, так как величины Х(t_m) и Х(t_k), вообще го­воря, зависимы. Если кроме Х(t_k) известна Х(t_l), где l 0 (t), под которым понимают отклонение случайного процесса X(t) от его среднего значения m_x(t), или

(4.2)

Тогда случайный процесс Xможно рассматривать как сумму двух составляющих: регулярной составляющей, равной математическому

ожиданию m_x(t), и центрированной случайной составляющей X 0 (t), т. е.

(4.3)

Очевидно, что математическое ожидание центрированного случайного процесса равно нулю:

(4.4)

Для того чтобы каким-то образом учесть степень разбросанности реализации случайного процесса относительно его среднего значения, вводят понятие дисперсии случайного процесса, которая равна мате­матическому ожиданию квадрата центрированного случайного про­цесса:

(4.5)

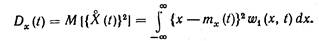
Дисперсия случайного процесса является неслучайной (регулярной) функцией времени D_x(t), значение которой в каждый момент времени t_k равно дисперсии соответствующего сечения Х(t_k) случайного процесса.

Легко показать,что математическое ожидание m_x(t), дисперсия D_x(t) и среднее значение квадрата x

2 (t) случайного процесса, имею­щие размерность квадрата случайной величины, связаны соотношением

(4.6)

Из (4.6) видно, что среднее значение квадрата случайного про­цесса x

2 (t) в определенной мере учитывает и среднее значение случай­ного процесса, и степень рассеяния его реализации относительно этого среднего значения, поэтому оно широко используется в качестве оцен­ки точности систем автоматического управления.

На практике часто бывает удобно пользоваться статистическими характеристиками случайного процесса, имеющими ту же размер­ность, что и сама случайная величина. К таким характеристикам от­носят:

среднее квадратическое значение случайного процесса

(4.7)

равное арифметическому значению квадратного корня из среднего зна­чения квадрата случайного процесса;

среднее квадратическое отклонение случайного процесса

(4.8)

равное арифметическому значению квадратного корня из дисперсии случайного процесса.

Из (4.7) и (4.8) видно,что среднее квадратическое значение x_с.к(t) и среднее квадратическое отклонение s_x(t) случайного процесса в общем случае не совпадают.

В заключение заметим, что хотя ни математическое ожидание, ни дисперсия случайного процесса ни в какой мере не характеризуютстепень статистической зависимости между сечениями случайно­го процесса в различные моменты времени, знания этих характеристик часто достаточно для решения многих задач теории автоматического управления.

Источник

Случайные процессы и функции

Случайный процесс Х(t) представляет собой функцию, которая отличается тем, что ее значения в любые произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность множества реализаций функций x_k(t), имеющих общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 131. В дальнейшем без дополнительных пояснений при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Рис. 13.1. Выборочные функции случайного процесса.

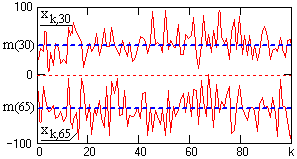
С практической точки зрения выборочная функция является результатом отдельного эксперимента, после которого данную реализацию x_k(t) можно считать детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. В каждый выбранный момент времени t₁ конкретная реализация процесса представляет собой случайную величину х₁ с определенной плотностью вероятности p(x₁, t₁), а ее среднее значение определяется усреднением по всем возможным реализациям в этот момент времени t₁. Полной статистической характеристикой такой системы является N-мерная плотность вероятностей р(x_n; t_n). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.

Рис. 13.2. Сечения случайного процесса X(t).

Одномерная функция распределения вероятностей (x, t_n) определяет вероятность того, что в момент времени t_n значение случайной величины X(t_n) не превысит значения x:

Очевидно, что в диапазоне значений вероятностей от 0 до 1 функция F(x, t) является неубывающей с предельными значениями F(-¥, t) = 0 и F(¥, t) = 1. При известной функции F(x, t) вероятность того, что значение X(t_n) в выборках будет попадать в определенный интервал значений [a, b] будет определяться выражением:

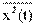
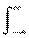
P(a 2 (t)>º = x 2 p(x; t) dx.

Функция дисперсии (variance) – второго центрального момента случайного процесса, определяет функцию среднего взвешенного значения (математического ожидания) квадрата разности Х(t)-m_x(t), которая называется флюктуационной частью процесса:

D_x(t) = M<[Х(t)-m_x(t)] 2 > = 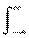[x(t)-m_x(t)] 2 p(x; t) dx. (

Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса (флюктуаций) значений случайного процесса по временной оси относительно математического ожидания процесса:

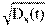
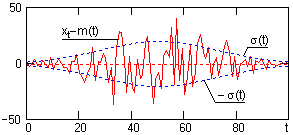
s_x(t) = . (13.3)

На рис. 13.4 приведен пример флюктуационной составляющей процесса X(t) (рис. 13.1) в одной из реализаций в сопоставлении со средним квадратическим отклонением ±s случайных величин от математического ожидания m(t).

p(x) = .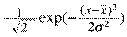

Это определяется тем, что в соответствии с «центральной предельной теоремой» распределение вероятностей для сумм независимых случайных величин, при которых нет доминирующих, стремится к нормальному закону по мере роста числа слагаемых, и не зависит от законов распределения слагаемых. Между тем физические случайные процессы обычно являются многопараметровыми, при этом случайность значений параметров, как правило, обусловлена их природой и также соответствует нормальным распределениям.

Двумерная плотность вероятностей. Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.

Двумерная плотность вероятностей p(x₁,x₂; t₁,t₂) определяет вероятность совместной реализации значений случайных величин Х(t₁) и Х(t₂) в произвольные моменты времени t₁ и t₂ и в какой-то мере уже позволяет оценивать динамику развития процесса. Двумерная плотность вероятностей описывает двумерную случайную величину n), X(t_m)> в виде функции вероятности реализации случайной величины X(t_n) в бесконечно малом интервале dx_n в окрестностях x_n в момент времени t_n при условии, что в момент времени t_m значение X(t_m) будет реализовано в бесконечно малом интервале dx_m в окрестностях x_m:

При двумерной плотности вероятности имеем:

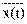
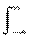
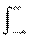
m_x(t) º = x₁(t₁) p(x₁,t₁; x₂,t₂) dx₁ dx₂. (13.1″)

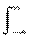
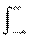
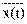
D_x(t) = s_x 2 (t)= [x₁(t₁)- ] 2 p(x₁,t₁; x₂,t₂) dx₁ dx₂. (13.2″)

Корреляционные функции случайных процессов. Характеристикой динамики изменения двумерной случайной величины n), X(t_m)> является корреляционная функция, которая описывает случайный процесс в целом:

Корреляционная функция представляет собой статистически усредненное произведение значений случайного процесса X(t) в моменты времени t_n и t_m по всем значениям аргументов t_n и t_m, а, следовательно, тоже является двумерной функцией. В терминах теории вероятностей корреляционная функция является вторым начальным моментом случайного процесса.

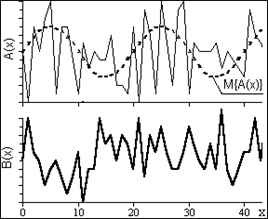
На рис. 13.5 приведены примеры реализаций двух случайных процессов, которые характеризуются одной и той же функцией математического ожидания и дисперсии.

Рис. 13.5.

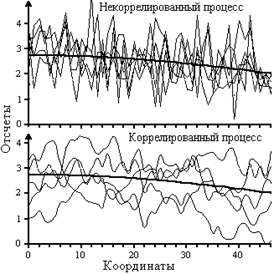
На рисунке видно, что хотя пространство состояний обоих процессов практически одно и то же, динамика развития процессов в реализациях существенно различается. Единичные реализации коррелированных процессов в произвольный момент времени могут быть такими же случайными, как и некоррелированных, а в пределе, во всех сечениях оба процесса могут иметь один и тот же закон распределения случайных величин. Однако динамика развития по координате t (или любой другой независимой переменной) единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, а, следовательно, в коррелированном процессе имеется определенная связь между последовательными значениями случайных величин. Оценка степени статистической зависимости мгновенных значений какого-либо процесса Х(t) в произвольные моменты времени t_n и t_m и производится функцией корреляции. По всему пространству значений случайного процесса X(t) корреляционная функция определяется выражением:

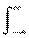
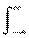
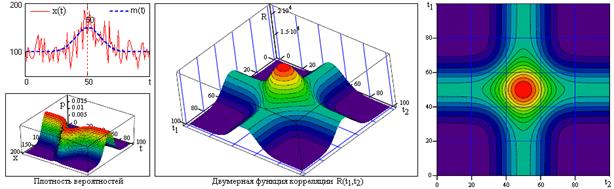
R_X(t_n, t_m) = x(t_n)x(t_m) p(x_n,t_m; x_n,t_m) dx_n dx_m, (9.1.4)

Рис. 13.6. Двумерная плотность вероятностей и корреляционная функция процесса X(t).

На рис. 13.6 приведена форма модельного случайного процесса X(t) в одной выборке со значительной и изменяющейся неслучайной составляющей. Модель задана на интервале 0-Т (Т=100) в дискретной форме с шагом Dt=1. Корреляционная функция вычислена по заданной плотности вероятностей модели.

При анализе случайных процессов второй момент времени t_m удобно задавать величиной сдвига t относительно первого момента, который при этом может быть задан в виде координатной переменной:

Функция, задаваемая этим выражением, обычно называется функцией автокорреляции случайного процесса.

Ковариационные функции. Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m_x(t) в моменты времени t_n и t_m и характеризует флюктуационную составляющую процесса:

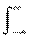
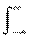
К_Х(t_n,t_m) = (x(t_n)-m_x(t_n)) (x(t_m)-m_x(t_m)) p(x_n,t_n; x_m,t_m) dx_n dx_m, (13.5)

В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции корреляции. При произвольных значениях m_x ковариационные и корреляционные функции связаны соотношением:

Нормированная функция автоковариации (функция корреляционных коэффициентов):

При t= 0 значение r_Х равно 1, а ФАК вырождается в дисперсию случайного процесса:

Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и корреляции (ковариации). Особой необходимости в отдельной функции дисперсии не имеется.

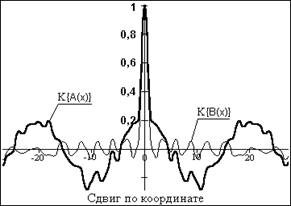
Примеры реализаций двух различных случайных процессов и их нормированных ковариационных функций приведены на рис. 13.7.

Рис. 13.7. Реализации и ковариационные функции случайных процессов.

Источник